Some other methods : MPn, CCSD

Moeller-Plesset Perturbation Theory (MP)

In perturbation theory, the solution to one problem is expressed in terms of another one solved previously. The perturbation should be small in some sense relative to the known problem.
MP2 is a good method for including electron correlation.

Coupled Cluster Singles and Doubles model (CCSD)

Perturbation methods add all types of corrections, e.g., S,D,T,Q,..to a given order (2nd, 3rd, 4th,…). The idea of Coupled cluster (CC) methods is to include all corrections of a given type to infinite order.

Results with CCSD and MP2

Reminder : DFT 6-31G*

HF=-117.9075562
Sum of electronic and thermal Energies=              -117.823399

MP2

With the basis set 6-31G*

Just before the Population Analysis, the result concerning energy :

 E2 =    -0.3850470013D+00 EUMP2 =    -0.11745546151999D+03

CCSD

With the basis set 6-31G*

The last part like below give you the energy of the molecule after calculation :

 DE(Corr)= -0.42378736     E(CORR)=     -117.49420188     Delta=-8.13D-08
 NORM(A)=   0.10868114D+01

Gap

Method	Energy (Hartree) propene	Energy (Hartree) cyclopropane	$Δ E$ (Hartree)	Error of (%, ref DFT)
DFT 6-31G*	-117.8234	-117.81012	0.013283	0
MP2	-117.45546	-117.44816	0.00730342	45
CCSD	-117.4942	-117.4832	0.01100599	17.1

We must admit that we have something completely different if we compare to the DFT. CCSD method gives the nearest results, but there is 17.1% of differences!

Molecular Mechanics (MM)

Principle

This method is the simplest and least computationally demanding calculations, because it consists to apply some Newton's mechanics in our calculations. Indeed, the molecule is modelled as a framework of spherical atoms which are bound together with elastic bonds which are described as springs.
Different MM could be applied and they differ in how consider the energy terms, e.g. which approximations we can consider in a specific case. Indeed the power of MM lies in the fact that you can specify many parameters and functions in order to get the best way to simulate your molecule. Thus the parameters that you can type in and the choice of the MM method depend of the type of molecule you have.

AMBER

This method is specially designed for treating large biomolecules.
We use simple harmonic functions for stretches and bends, cosine for torsion, and the standard functions for electrostatic and Van der Waals interactions.

Other methods exist : UFF, Dreiding.

Advice break

If you want More explanations about Molecular Mechanics in Gaussian click on the link and you will find all that you need about MM in Gaussian.

Advantages and disadvantages

The electrons are neglected in this method so electronically excited states can not be treated without other specific parameters.
But the cost of these calculations is very low which makes it very attractive for calculations of large systems like proteins. And a good way to increase the accuracy of this method is to couple this one with the quantum mechanic.

Semi-empirical methods

MNDO,AM1,PM3

They are all self-consistent field (SCF) methods, they take into account electrostatic repulsion and exchange stabilization, and all calculated integrals are evaluated by approximate means.
Further, they all use a restricted basis set of one s orbital and three p orbitals (px, py, and pz) and sometimes five d orbitals per atom and ignore overlap integrals in the secular equation.

So you can easily imagine that with these approximation the results are really approximate, so now have a look at the results to really understand what a semi empirical method is...

The results

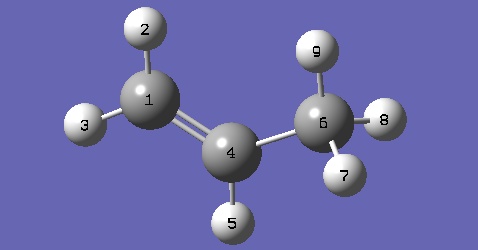
The Bond length

Bond	DFT ; 6-31G*	AM1	PM3	MNDO	AM1/DFT error (%)	PM3/DFT error (%)	MNDO/DFT error (%)
1-2	1.0885	1.0978	1.0865	1.0889	0.85	0.18	0.037
1-4	1.3333	1.3312	1.3279	1.3404	0.16	0.4	0.53
4-6	1.5021	1.4763	1.4802	1.4959	1.72	1.46	0.41
6-7	1.0985	1.1191	1.0983	1.4959	1.88	0.018	36.2

Despite it is a semi empirical method we get good results concerning the bond length.

Energy

Just below the table resume the energy that give the different theories and the approximate errors of the semi empirical calculations compared with the DFT (the best results that we get compared with the experimental results).

Method	Energy (Hartree) propene	Energy (Hartree) cyclopropane	$Δ E$ (Hartree)	Error of (%, ref DFT)
DFT 6-31G*	-117.8234	-117.81012	0.013283	0
AM1	0.01038943	0.02824908	0.01785965	34.5
PM3	0.01012597	0.02584785	0.01572188	18.4
MNDO	0.00784966	0.01778439	0.00993473	25.2

So by comparing the results concerning the energy and the bond length we can deduce that semi empirical methods could be a good approximation but the better approximation especially for the bond length are the AM1 and the PM3 methods

Back to Resgrp:comp-photo-c3h6-tutorial