More explanations about Molecular Mechanics in Gaussian

word file concerning MM

Molecular Mechanics in Gaussian

A basic MM potential function is usually of the form :

$E^{t o t a l} = \sum_{b o n d s} K_{r} (r - r_{e q})^{2} + \sum_{a n g l e s} K_{θ} (θ - θ_{e q})^{2} + \sum_{d i h e d r a l s} \frac{V_{n}}{2} [1 + \cos (n ϕ - γ)] + \sum_{i < j} [\frac{A_{i j}}{r_{i j}^{12}} - \frac{B_{i j}}{r_{i j}^{6}} + \frac{q_{i} q_{j}}{ε r_{i j}}] (e q . 1)$

The terms on the r.h.s. of eq. 1 are the stretch terms, bend terms, torsional terms, and non-bonded interactions. The particular forms of the individual functions in $(e q . 1)$ are from the Amber force field, which uses simple harmonic functions for stretches and bends, cosine for torsion, and the standard functions for electrostatic and van der Waals interactions.
Other force fields may use different functions, or have types of terms that are not included in the Amber force field, such as dipole interactions or stretch-bend couplings.

To set up the potential function, the program needs to know which structures (stretches, bends, and torsions, etc.) exist in the system, and which parameters and functions need to be used for them.
The structures can be identified from the connectivity, which is the list of bonds that are present in the system. By default, Gaussian constructs this list, and it does a good job if the input geometry is reasonable and the bond orders (single, double, etc.) are all well defined. However, if the calculation is started with a more approximate geometry, or there are bonds that are not easy to identify, it is safer to specify the connectivity list explicitly in the input stream. This is done using the Geom=Connectivity keyword. Besides the connectivity, the program needs to know which parameters and functions to use. This is more complicated, and is the topic of the remainder of this document.
We start with the most basic ways to run MM calculations in Gaussian, and step by step explain all the mechanisms available in Gaussian to specify parameters and functions.

Atom types

The parameters and functions are determined from the MM atom types, which are assigned to the centers in the system.
For example, in the Amber force field, a normal $s p^{3}$ hybridized carbon atom is CT, and a hydrogen atom connected to it has the label HC. An energy calculation on methane would look like this (IOp(4/33=3) does not affect the calculation, but prints the information that is referred to in the next paragraphs) :

#P Amber Geom=Connectivity IOp(4/33=3)

Methane

0 1
C-CT--0.4    -0.85  0.42  0.00
H-HC-0.1     -0.50 -0.57  0.00
H-HC-0.1     -0.50  0.93  0.87
H-HC-0.1     -0.50  0.93 -0.87
H-HC-0.1     -1.92  0.42  0.00

1 2 1.0 3 1.0 4 1.0
2
3
4

For a single element, such as carbon, there can be many different MM atom types. Which one to use depends on aspects such as the hybridization, chemical environment, etc.
Some programs can automatically determine the atom types. Gaussian can do this for the UFF and Dreiding force fields, but for the Amber force field the atom types need to be specified explicitly.
Just as with the connectivity, the automatic assignment of UFF and Dreiding atom types is only reliable for well-defined systems, and it is often safer to specify them explicitly in the input.

Atomic charges

For the electrostatic interactions to be computed, partial atomic (point) charges need to be assigned to the centers in the system.
Gaussian can do this automatically using the QEq formalism, by specifying the QEq keyword (for example, Dreiding=QEq).
These charges depend on the geometry and are computed at the beginning of the calculation, but are not updated during the course of an optimization or other process that changes the geometry.

The actual values of the charges can also be specified in the input. This is done after the atom label.
In the methane example, the carbon gets a $- 0.4$ charge, and the hydrogens each $+ 0.1$ .

The potential function

When we run the methane example, we find the following lines in the output:

Atomic parameters:
 Center  VDW
      1 1.9080  .1094000
      2 1.4870  .0157000
      3 1.4870  .0157000
      4 1.4870  .0157000
      5 1.4870  .0157000
 Molecular mechanics terms:           
 NBDir 3 1      0      0
 HrmStr1 1-2  340.00 1.0900
 HrmStr1 1-3  340.00 1.0900
 HrmStr1 1-4  340.00 1.0900
 HrmStr1 1-5  340.00 1.0900
 HrmBnd1 2-1-3  35.00 109.50
 HrmBnd1 2-1-4  35.00 109.50
 HrmBnd1 2-1-5  35.00 109.50
 HrmBnd1 3-1-4  35.00 109.50
 HrmBnd1 3-1-5  35.00 109.50
 HrmBnd1 4-1-5  35.00 109.50 
 NBPair 2-1 3 1      0      0 -1.000 -1.000
 NBPair 3-1 3 1      0      0 -1.000 -1.000
 NBPair 3-2 3 1      0      0 -1.000 -1.000
 NBPair 4-1 3 1      0      0 -1.000 -1.000
 NBPair 4-2 3 1      0      0 -1.000 -1.000
 NBPair 4-3 3 1      0      0 -1.000 -1.000
 NBPair 5-1 3 1      0      0 -1.000 -1.000
 NBPair 5-2 3 1      0      0 -1.000 -1.000
 NBPair 5-3 3 1      0      0 -1.000 -1.000
 NBPair 5-4 3 1      0      0 -1.000 -1.000

Under “Molecular mechanics terms“ is the list of terms that make up the total potential function.
For example, there is a (stretch) term between atoms 1 and 2 (and 1-3 and 1-4) that uses the function called HrmStr1. The force constant is 340 kcal/(mol Å²), and the equilibrium bond length is 1.09 Å.

How does Gaussian know that it needs to use the HrmStr1 potential function with those values?

From the connectivity the program knows that a stretch term exists between centers 1 and 2. These centers correspond to MM types CT and HC. Now the code has simply tables ‘hardwired’ in which the program can look up the parameters and functions. One of the entries in the table is HrmStr1 CT HC 340 1.09, which matches the stretch term in question.

Gaussian has a library of potential functions. The functions, required parameters, and units are listed in the manual.

Atomic parameters

In many cases, an MM parameter depends only on the atom type of one center, and not on the all the centers that are involved in a certain term.
An example is the van der Waals interaction. Each atom has its own van der Waals parameters, and they are combined when the term is evaluated. In other words, there are no Van der Waals parameters specifically for the CT-HC (or CT-CT or HC-HC) interaction, but there are van der Waals parameters for CT and HC individually.

These ‘atomic parameters’ are listed right before the Molecular mechanics terms in the output.
The advantage is clear: the number of parameters scales linearly with the number of different atom types instead of quadratically (in the case of terms that involve two centers) or worse, which makes the development of the force field much easier. In fact, some force fields, such as UFF and Dreiding, only use atomic parameters. Even stretching force constants and equilibrium bond lengths are then derived from parameters than only depend on a single atom type.
These force fields are much more generally applicable (there are no missing parameters), but the accuracy is compromised.

Non-bonded terms

The list of non-bonded terms is formed by all possible pairs of atoms, and thus the number of terms scales quadratically with the number of atoms in the systems.

Furthermore, interactions between atoms that are close together, based on the number of bonds that separate them, are usually scaled down. Typically one and two bond separated interactions are scaled to zero, and three bond separated interactions are scaled with a factor between zero and one, depending on the force field.
It is clear that for larger systems, the list of non-bonded terms can become very long. In most MM programs, cutoffs are used the keep the list manageable. In Gaussian we use a less common approach to efficiently deal with the non-bonded interactions.

The total non-bonded energy in the system can be written as:

$E^{N B} = \sum_{i}^{N} \sum_{i}^{j < i} [s_{i j}^{v d w} E_{i j}^{v d w} + s_{i j}^{Q} E_{i j}^{Q}] (e q . 2)$

$E_{i j}^{v d w}$ and $E_{i j}^{Q}$ are the van der Waals and electrostatic interaction between centers $i$ and $j$ , and $s$ are the scaling factors.

Now we rewrite this summation

$E^{N B} = \sum_{i}^{N} \sum_{j}^{j < i} [E_{i j}^{v d w} + E_{i j}^{Q}] - \sum_{i}^{N} \sum_{j}^{j < i} [(1 - s_{i j}^{v d w}) E_{i j}^{v d w} + (1 - s_{i j}^{Q}) E_{i j}^{Q}] (e q . 3)$

The first term on the r.h.s. computes all the pairs without scaling.
The second term subtracts the interactions that were supposed to be scaled, and thus ‘overcounted’ by the first term.
The first term can be evaluated in an efficient manner, using linear scaling and other techniques. Now most of the pairs in the second term give a zero interaction (provided the system is not too small), because $s_{i j}$ is one for most pairs. We simply keep a list of those pairs that give non-zero interactions to take care of the second term of $e q . 3$ . The result is an efficient algorithm that does not use cutoffs, and only needs a list of which the length scales linearly with the size of the system.
In the methane example, the NBDir term (in the Molecular mechanics terms list) instructs the computation of all the interactions in the first term on the r.h.s. in eq. 3 (there is only one entry in the list, that takes care of all the interactions).
The NBPair entries take care of the second term on the r.h.s. in $e q . 3$ .
In the methane example, all the scale factors in the NBPair terms are –1, because in such a small molecule no atoms are separated further than two bonds (the final non-bonded interaction will therefore be zero).

Missing parameters

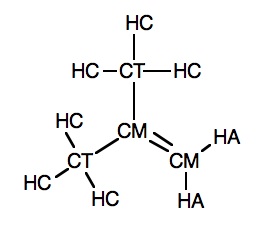
We run an Amber calculation on 2-methylpropene (in which the $s p^{2}$ hybridized carbons are CM, and the $s p^{3}$ hybridized carbons are CT).

#P amber

2-methylpropene

0 1
 C-CM       -2.53    0.19    0.00
 H-HA       -2.00   -0.73    0.00
 H-HA       -3.60    0.19    0.00
 C-CM       -1.86    1.37    0.00
 C-CT       -2.63    2.70    0.00
 H-HC       -1.93    3.51    0.07
 H-HC       -3.24    2.76   -0.88
 H-HC       -3.24    2.76    0.85
 C-CT       -0.32    1.37    0.00
 H-HC        0.03    1.87   -0.83
 H-HC        0.03    1.87    0.81
 H-HC        0.03    0.36   -0.00

The program terminates with an error message:

 Angle bend undefined between atoms    2    1    3
 Angle bend undefined between atoms    5    4    9       
 MM function not complete

Atoms 2-1-3 correspond to types HA-CM-HA, and 5-4-9 correspond to CT-CM-CT.

Apparently there are no entries for these bending terms in the hardwired tables, even though the atom types and the sequence are (chemically) perfectly reasonable.
The reason is that the Amber force field has been developed specifically for biochemical systems, in which these particular sequences of atom types do not occur.
Therefore the parameters have not been determined, and are ‘missing’ from the hardwired tables. Gaussian only checks if functions are found for all the stretches and bends. Torsional and other terms are simply not used in the total potential function if no entries exist in the tables.

Defining new atom types

Gaussian ‘knows’ about the standard MM atom types from the Dreiding, UFF, and Amber force fields. However, when a system is studied that these force fields are not parameterized for, none of the available atom types may be suitable. In that case one can define a new atom type, simply by using that label in the input.
Of course, these new atom types will not exist in the hardwired tables, and consequently result in an incomplete MM function error termination.

Adding and replacing parameters

When hardwired parameters are not available, either from incomplete tables or the introduction of new atom types, they need to be specified in the input stream.
Of course, the hard part is how to determine those parameters in the first place. Quite often they can be found in the literature, otherwise they need to be derived from experimental or accurate computational data, but that is beyond the scope of this document.

To specify new parameters, use the Amber=HardFirst keyword, and add them to the input stream.

The 2-methylpropene example then looks like:

#P amber=hardfirst

2-methylpropene

0 1
 C-CM       -2.53    0.19    0.00
 H-HA       -2.00   -0.73    0.00
 H-HA       -3.60    0.19    0.00
 C-CM       -1.86    1.37    0.00
 C-CT       -2.63    2.70    0.00
 H-HC       -1.93    3.51    0.07
 H-HC       -3.24    2.76   -0.88
 H-HC       -3.24    2.76    0.85
 C-CT       -0.32    1.37    0.00
 H-HC        0.03    1.87   -0.83
 H-HC        0.03    1.87    0.81
 H-HC        0.03    0.36   -0.00

HrmBnd1 CT CM CT 70.0 120.0
HrmBnd1 HA CM HA 40.0 120.0

The values in this example are a rough guess based on existing Amber parameters. The HardFirst keyword indicates that the hardwired tables are checked first. Only if there is no entry found in the hardwired tables, the programs try to find a match in the input stream. SoftFirst and SoftOnly are related keywords, and specify that the soft parameters (from the input stream) need to be checked first, followed by the hardwired set, or even exclusively. It is clear that with the SoftFirst keyword, one can effectively replace parameters from the hardwired set. With SoftOnly, the complete force field definition needs to be provided in the input.

The “Non-Bonded Master Function”

Gaussian computes the non-bonded interactions following $e q . 3$ , and as shown before, uses one NBDir and many NBPair terms for the total potential function.
When the non-bonded interactions are specified in the input (using HardFirst, SoftFirst, or SoftOnly), the non-bonded interactions do not need to be specified with the NBDir and NBPair entries, because this would be quite cumbersome. Instead, one can use the NonBon function, which is expanded by the program into the appropriate NBDir and NBPair entries.

Wildcards

Wildcards can be used in the input stream. In this example, all the bends with central atom CM will have the same values:

HrmBnd1 * CM * 70.0 120.0

One could also give a generic entry using wildcards, but let other entries be specific:

HrmBnd1 *  CM *  70.0 120.0
HrmBnd1 HA CM HA 40.0 120.0

The program assigns the entry that is the most specific. If there happen to be different entries that are equally specific, the program terminates with the Multiple matching entries error message. This can be avoided by specifying the FirstEquiv or LastEquiv keywords, which tell to use the first match or last match, respectively, of two or more equivalent matches.
However, it is likely that the Multiple matching entries message indicates some inconsistency in the soft parameter set, which needs to be investigated before using FirstEquiv or LastEquiv.

The wildcards do not affect whether an entry from the hardwired or soft set is used. When SoftFirst is specified, even a matching entry in the input stream that has three wildcards, will have priority over any matching entry from the hardwired set.

Substructures

Substructures provide a mechanism to let structural information determine which parameters are used.
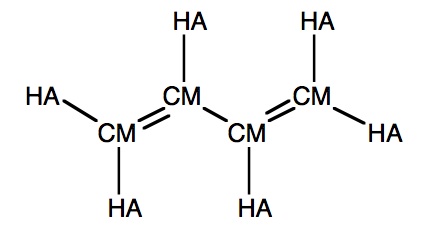
Say we want to calculate butadiene. The carbon atoms are all of type CM, but two bonds are formally double, and one is single. In the examples above, however, the force constant and equilibrium bond length of a stretching term only depend on the atom types, so we cannot assign different values for the different types of bonds.
With the substructures we can restrict entries in the soft set to a specific bond order.
The butadiene calculation becomes:

#P Amber=SoftFirst Geom=Connectivity

Title Card Required

0 1
 C-CM    -2.49  -0.07   0.00
 H-HA    -1.96  -1.00   0.00
 H-HA    -3.56  -0.07   0.00
 C-CM    -1.82   1.09   0.00
 H-HA    -2.35   2.02   0.00
 C-CM    -0.28   1.09   0.00
 H-HA     0.24   0.16   0.00
 C-CM     0.39   2.26  -0.00
 H-HA    -0.13   3.19   0.00
 H-HA     1.46   2.26  -0.00

 1 2 1.0 3 1.0 4 2.0
 2
 3
 4 5 1.0 6 1.0
 5
 6 7 1.0 8 2.0
 7
 8 9 1.0 10 1.0
 9
 10

HrmBnd1 HA CM HA 40.0 120.0
HrmBnd1 CM CM CM 70.0 120.0
HrmStr1-1 CM CM 350.0 1.51
HrmStr1-2 CM CM 500.0 1.37

Again, the actual values used for the parameters in this example are only for ‘illustration purposes only’. In fact, if we were serious about this calculation, we would also enter torsional parameters that are specific for single or double central bonds, which can be done with the substructures mechanism as well.

Besides the bond order, other examples of substructures are whether the term lies in a cyclic structure, how many hydrogens are connected, etc.
For example, HrmStr1-2-4 specifies that this term applies only to a stretch that involves a double bond that lies in a four-membered ring. A substructure value of zero is similar to a wildcard: HrmStr1-0-4 specifies that the term applies to a stretch of any bond order, but it must be in a four-membered ring.

In a number of cases, structural information can also be filled in ‘on-the-fly’ as parameter by the program.
For example, when the “HrmStr3 * * -1.0 0.1332” (from the UFF forcefield) function is specified in the input file, the “-1.0” is replaced by the bond order (a positive value instead of –1.0 would not have been replaced by the program).

Step-down tables

Wildcards provide a mechanism for specifying generic parameters (that do not explicitly depend on each of the atom types involved in a particular term). The step-down tables have the same purpose, but are more sophisticated.
Consider the following example, which is a part taking from the UFF force field:

UseTable UFFBnd2 #3       
UseTable UFFBnd3 #3
StepDown UFFBnd2 0 1 0
StepDown UFFBnd2 0 2 0
StepDown UFFBnd3 0 1 0    
StepDown UFFBnd3 0 2 0    
Table #3 C_R    Trig      
Table #3 N_R    Trig      
Table #3 H_     Lin       
Table #3 Li     Lin       
UFFBnd3   0 C_3   0 109.471  -1.0 -1.0 0.1332    
UFFBnd3   0 N_3   0 106.700  -1.0 -1.0 0.1332    
UFFBnd3   0 N_2   0 111.200  -1.0 -1.0 0.1332    
UFFBnd3   0 O_3   0 104.510  -1.0 -1.0 0.1332    
UFFBnd2-0-2   0 Lin   0 2        -1.0 -1.0 0.1332
UFFBnd3-0-3   0 Lin   0 180.0    -1.0 -1.0 0.1332
UFFBnd3-0-4   0 Lin   0 180.0    -1.0 -1.0 0.1332
UFFBnd3-0-5   0 Lin   0 180.0    -1.0 -1.0 0.1332
UFFBnd3-0-6   0 Lin   0 180.0    -1.0 -1.0 0.1332
UFFBnd3-0-2   0 Trig  0 120.0    -1.0 -1.0 0.1332
UFFBnd2-0-3   0 Trig  0 3        -1.0 -1.0 0.1332
UFFBnd3-0-4   0 Trig  0 120.0    -1.0 -1.0 0.1332
UFFBnd3-0-5   0 Trig  0 120.0    -1.0 -1.0 0.1332
UFFBnd3-0-6   0 Trig  0 120.0    -1.0 -1.0 0.1332

Say there is a H_ - N_R - H_ bend sequence in the system (H_ and N_R are atom types in the UFF force field). In the parameter file, the only bending functions are UFFBnd2 and UFFBnd3, and for those the step-down table #3 is used (this is indicated by the UseTable entries). Now the Table #3 for H_ is “H_ Lin”. This means that Lin is an alternative atom type for H_ (in this example, we only specify one alternative atom type, but there can be many more). Trig is the first alternative atom type N_R in Table #3.
The StepDown entries indicate the step-down sequence.
For both UFFBnd2 and UFFBnd3, the first step-down entry is “0 1 0”. The 0 denotes wildcard, and 1 denotes that the original atom type must be matched. In other words, in the first pass, the “H_ - N_R - H_” sequence becomes “* - N_R - *”. It is clear that no match is found.
The second entry in the step-down sequence is “0 2 0”. The 0 denotes again wildcard, and the 2 denotes the second entry in the table (thus the first alternative atom type), thus is will search for “ * - Trig - * “. Now it indeed finds an entry (which entry is used, incidentally, depend in this case also on the substructures!).

Summary

Gaussian has very powerful means to specify parameters. Through the concept of a library of potential functions, and mechanism such as the step-down tables, nearly any force field can be specified provided the potential functions are available in the library (which is continuously expanded). No coding is then required.
Unfortunately, the parameter specification in the input can become rather complicated. It helps to use the ‘input file versions’ of the UFF, Dreiding, and Amber force field constructed by us as template.

More explanations on GAUSSIAN website Molecular Mechanics Methods

Back to Other methods