Resgrp:comp-photo/VB
Valence Bond Analysis
Introduction
The physical basis of VB theory is the notion that a chemical bond is associated with the pairing of the electrons in the (singly occupied) valence orbitals of the atoms concerned, and its aim is to construct wave functions in which all possible bonds are described in terms of spin pairing. Mathematically, this means that one must deal with many-determinant wave functions constructed directly from atomic orbitals by admitting all allocations of spin factors and coupling the spins in pairs to a resultant S = 0. In essence, in the VB formalism there is a direct connection between the electron pairs which are spin coupled and molecular structure (i.e. the geometry corresponds to “where the bonds are”).
In general, the total energy of a system is, according to the London formula:
being Q the Coulomb integral and K the exchange integral, whose behaviour can be rationalized by using the Heitler-London expression for two electrons:
where the first term is the two-electron-exchange repulsion integral, and the second one is the one-electron-exchange integral (nuclear-electron attraction) times the overlap integral between orbitals i and j.
Then the essence of the theory is that paired spins correspond to chemical bonds. The paired spins label regions in the molecule where we might expect chemical bonds to occur. Then we can construct spin eigenfunctions (with associated Rumer diagrams) using the spin-pairing method. A function constructed in this way is associated pictorically with a possible way of drawing classical chemical bonds in order to accommodate all the electrons from a set of singly occupied valence orbitals. In this way, each Rumer diagram acquires a certain “chemical” significance. It is then plausible to assume that in favourable cases a single spin-paired structure may give a reasonably good description of the electronic state.
On the other hand, since depends on orbital overlap, then we have to take into account the distance between them (if the distance is too large, we can assume that = 0) as well as their directionality (that is, if two p orbitals in adjacent bonds are perpendicular, then = 0 whatever the distance is). Therefore, if T = 0, the total energy will be the same for both states (crossing). You can find a detailed discussion in:
- F. Bernardi, M. Olivucci, M.A. Robb. Predicting Forbidden and Allowed Cycloaddition Reactions: Potential Surface Topology and Its Rationalization. Acc. Chem. Res. 23 (1990) 405-412.
- S. Vanni, M. Garavelli, M.A. Robb. A new formulation of the phase change approach in the theory of conical intersections. Chem. Phys. 347 (2008) 46-56.
MMVB
The idea is to use a combination of molecular mechanics (MM) and valence bond (VB) theory to simulate MC-SCF results.
See the article: F. Bernardi, M. Olivucci, M.A. Robb. Simulation of MC-SCF Results on Covalent Organic Multi-Bond Reactions: Molecular Mechanics with Valence Bond (MM-VB). J. Am. Chem. Soc. 114 (1992) 1606-1616.
For a detailed description of the VB applications in photochemistry, see:
- F. Bernardi, M. Olivucci, M.A. Robb, G. Tonachini. Can a Photochemical Reaction Be Concerted? A Theoretical Study of the Photochemi18cal Sigmatropic Rearrangement of But-1-ene. J. Am. Chem. Soc. 114 (1992) 5805-5812.
- M.J. Bearpark, M. Deumal, M.A. Robb, T. Vreven, N. Yamamoto, M. Olivucci, F. Bernardi. Modelling Photochemical [4+4] Cycloadditions: Conical Intersections Located with CASSCF for Butadiene+Butadiene. J. Am. Chem. Soc. 119 (1997) 709-718.
The typical input file may be:
amber=(softonly,lastequiv) test nosymm geom=connectivity SP
iop(1/19=11,1/117=00001,1/119=-3,2/15=1,4/31=2,4/33=2)
MMVB analysis
0 1
C-MM101 -0.620151 -0.067453 -1.190099
C-MM101 -1.416685 -0.268994 0.000000
C-MM101 0.174614 1.160606 -1.204823
C-MM101 0.545282 1.753453 0.000000
C-MM101 0.174614 1.160606 1.204823
C-MM101 -0.620151 -0.067453 1.190099
C-MM101 0.777908 -1.455653 -0.728991
C-MM101 0.777908 -1.455653 0.728991
H-MM5 -1.036876 -0.367046 -2.137967
H-MM5 -2.183420 -1.024540 0.000000
H-MM5 0.533588 1.549366 -2.140507
H-MM5 1.140713 2.649438 0.000000
H-MM5 0.533588 1.549366 2.140507
H-MM5 -1.036876 -0.367046 2.137967
H-MM5 1.670182 -1.111139 -1.222392
H-MM5 0.338023 -2.313857 -1.210918
H-MM5 1.670182 -1.111139 1.222392
H-MM5 0.338023 -2.313857 1.210918
(The geometry must include the type of atom)
1 2 21.0 3 21.0 4 10.0 5 10.0 6 10.0 7 10.0 8 10.0 9 1.0
2 1 21.0 3 10.0 4 10.0 5 10.0 6 21.0 7 10.0 8 10.0 10 1.0
3 1 21.0 2 10.0 4 21.0 5 10.0 6 10.0 7 10.0 8 10.0 11 1.0
4 1 10.0 2 10.0 3 21.0 5 21.0 6 10.0 7 10.0 8 10.0 12 1.0
5 1 10.0 2 10.0 3 10.0 4 21.0 6 21.0 7 10.0 8 10.0 13 1.0
6 1 10.0 2 21.0 3 10.0 4 10.0 5 21.0 7 10.0 8 10.0 14 1.0
7 1 10.0 2 10.0 3 10.0 4 10.0 5 10.0 6 10.0 8 21.0 15 1.0 16 1.0
8 1 10.0 2 10.0 3 10.0 4 10.0 5 10.0 6 10.0 7 21.0 17 1.0 18 1.0
9 1 1.0
10 2 1.0
11 3 1.0
12 4 1.0
13 5 1.0
14 6 1.0
15 7 1.0
16 7 1.0
17 8 1.0
18 8 1.0
(This is the connection matrix: 21.0 stands for a double bond interaction, 10.0 for a single-bond interaction. For instance, in benzene all the connections between neighbouring C atoms must be 21.0, and between non-neighbouring C atoms must be 10.0; in the case of optimizations, it is better to change 10.0 to 11.0). The C-H bonds are described just by MM (1.0).
The IOP 117 controls the calculation. The main parameters are:
C2IOp(117)
C IOp(117) ... MMVB control:
C 0 ... No MMVB
C 1 ... Do MMVB calculation.
C 000 ... Activate Bridging Corrections to Kij and Qij (Default)
C 0000 ... No Conical Intersection Search (Default)
C 1000 ... Search For Conical Intersection For (LRoot,LRoot-1)
C 00000 ... Do not Delete any Coulombic Qij.
C 10000 ... Specify Qij to delete.
C 0000000 ... Solve VB problem numerically with Lanczos
C 1000000 ... Solve VB problem analytically
C 00000000 ... Hartree-Waller functions for singlets or triplets
C 10000000 ... Slater determinant
The IOP 119 is also important:
C2IOp(119)
C IOp(119) ... Control Initial Lanczos Vector (ILzVec)
C -1 ... Read guess by card in input file
C -2 ... Use the largest elements of H as a guess
C -3 ... Use the five largest contributions of H as a guess
Sometimes there may be a problem in solving the eigenvalue problem due to the initial vector in the Lanczos method (an adaptation of power methods to find eigenvalues and eigenvectors of a square matrix). Then it is advisable to use, by default, the option "-3" to make sure that your initial vector is well-balanced. Another option is to use an initial vector in the input file. For instance, in a system with just three configurations, we can write the vector after the connection matrix (leaving a blank line):
1 1.000000
2 1.000000
3 1.000000
In addition, it is advisable to delete the coulombic integrals between non-neighbouring atoms if your aim is to optimize a structure.
On the other hand, the IOPs 4/31=2,4/33=2 are for the number of states and to print everything, respectively.
In the output we can find the as well as the elements of the density matrix, and the transition density matrix elements:
Pi Kij and Qij for I,J= 2 1
K0ij= -0.56278165E-01 Kij= -0.50723878E-01
Q0ij= -0.25559997E-01 Qij= -0.31740808E-01
Pi Kij and Qij for I,J= 3 1
K0ij= -0.56034953E-01 Kij= -0.55333517E-01
Q0ij= -0.31493372E-01 Qij= -0.32273930E-01
Sigma Kij and Qij for I,J= 3 2
K0ij= -0.53944673E-02 Kij= -0.46567881E-02
Q0ij= -0.18172581 Qij= -0.18395974
Spin Density Matrix
Root 1
1 1 0.000
2 1-0.423 2 2 0.000
3 1-0.424 3 2 0.478 3 3 0.000
4 1-0.548 4 2-0.984 4 3 0.480 4 4 0.000
5 1-0.581 5 2 0.478 5 3-0.974 5 4 0.480 5 5 0.000
6 1-0.497 6 2-0.423 6 3-0.581 6 4-0.548 6 5-0.424 6 6 0.000
7 1 0.979 7 2-0.563 7 3-0.569 7 4-0.440 7 5-0.410 7 6-0.506
7 7 0.000
8 1-0.506 8 2-0.563 8 3-0.410 8 4-0.440 8 5-0.569 8 6 0.979
8 7-0.490 8 8 0.000
Transition Density Matrix
1 1 0.000
2 1-0.564 2 2 0.000
3 1 0.386 3 2 0.151 3 3 0.000
4 1-0.097 4 2 0.000 4 3-0.263 4 4 0.000
5 1 0.254 5 2-0.151 5 3 0.000 5 4 0.263 5 5 0.000
6 1 0.000 6 2 0.564 6 3-0.254 6 4 0.097 6 5-0.386 6 6 0.000
7 1 0.045 7 2 0.523 7 3-0.382 7 4 0.151 7 5-0.363 7 6 0.024
7 7 0.000
8 1-0.024 8 2-0.523 8 3 0.363 8 4-0.151 8 5 0.382 8 6-0.045
8 7 0.000 8 8 0.000
Ab initio Pij's
This is a CASSCF implementation of VB based method for the analysis of bonding in organic molecules. The method uses the spin-exchange density matrix P with localized MOs. The index evaluates the contributions of the determinants to the CASSCF wave function and is used to generate resonance formulas.
See the article: L. Blancafort, P. Celani, M.J. Bearpark, M.A. Robb. A valence-bond-based complete-active-space self-consistent-field method for the evaluation of bonding in organic molecules. Theor. Chem. Acc. 110 (2003) 92-99.
The route section must be similar to:
- p CASSCF(8,8,nofulldiag)/6-31G*,Pop=AllOrbitals,gfinput,iop(4/46=1,5/39=2300001,5/42=1),nosymm,guess=read,
scf=maxcycle=999,geom=check
The IOP 5/42=1 is needed to localize the MOs. The results are given in the output as:
Pij Operator.
The signs are fixed to have E=Sum Pij*Kij with Kij<0
e.g. Pij=1 for singlet 2e/2o
1 0.168
2 -0.490 0.170
3 -0.525 -0.490 0.163
4 0.455 -0.490 -0.398 0.163
5 -0.455 0.150 -0.559 -0.449 0.137
6 -0.538 -0.684 -0.311 -0.311 0.143 0.063
7 -0.392 0.150 -0.449 -0.559 -0.773 0.143 0.137
8 -0.394 -0.490 0.455 -0.525 -0.392 -0.538 -0.455 0.167
Pij a a a a
1 0.000
2 -0.495 0.000
3 -0.504 -0.490 0.000
4 -0.092 -0.490 -0.444 0.000
5 -0.493 -0.239 -0.522 -0.470 0.000
6 -0.503 -0.555 -0.406 -0.406 -0.290 0.000
7 -0.473 -0.239 -0.470 -0.522 -0.603 -0.290 0.000
8 -0.444 -0.495 -0.092 -0.504 -0.473 -0.503 -0.493 0.000
Pij a a b b
1 0.168
2 0.005 0.170
3 -0.021 0.000 0.163
4 0.547 0.000 0.046 0.163
5 0.039 0.389 -0.037 0.021 0.137
6 -0.035 -0.128 0.095 0.095 0.433 0.063
7 0.081 0.389 0.021 -0.037 -0.170 0.433 0.137
8 0.050 0.005 0.547 -0.021 0.081 -0.035 0.039 0.167
Example: benzene
For the ground state of benzene, the value for the between neighbouring C atoms are (theoretically) 0.40. The labeling for C atoms (in MMVB) or localized molecular orbitals (in ab initio) are:
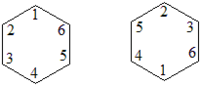
The MMVB are:
Spin Density Matrix
Root 1
1 1 0.000
2 1 0.434 2 2 0.000
3 1-0.914 3 2 0.434 3 3 0.000
4 1-0.041 4 2-0.914 4 3 0.434 4 4 0.000
5 1-0.914 5 2-0.041 5 3-0.914 5 4 0.434 5 5 0.000
6 1 0.434 6 2-0.914 6 3-0.041 6 4-0.914 6 5 0.434 6 6 0.000
In this case, as you can see in the input below, the following are deleted:
Pairs of Qij integrals deleted in MMVB:
3 1
4 1
5 1
4 2
5 2
6 2
3 1
5 3
6 3
4 1
4 2
6 4
5 1
5 2
5 3
6 2
6 3
6 4
You can see an example of optimization as well.
On the other hand, the ab initio are:
Pij a a b b
1 0.174
2 0.130 0.174
3 -0.076 0.337 0.174
4 0.337 -0.076 0.130 0.174
5 -0.076 0.337 -0.076 0.337 0.174
6 0.337 -0.076 0.337 -0.076 0.130 0.174
Here go the inputs/outputs:
MMVB single point:
Media:benzene_S0_mmvb.gjf
Media:benzene_S0_mmvb.log
MMVB optimization:
Media:benzene_S0_mmvb_opt.gjf
Media:benzene_S0_mmvb_opt.log
ab initio Pij analysis:
