MRD:phw417

This report has been plagiarised from here and here.

Exercise 1: H + H₂system

Dynamics from the transition state region:

On a potential energy surface diagram, the transition state is mathematically defined as the saddle point. The transition state has partial derivatives of zero with respect to the molecular distances, (f_x = 0 and f_y = 0) as it is the maximum on the minimum energy path linking reactants and the products . To distinguish between a local minimum or a local maximum and a transition state, the second derivatives of the potential energy surface with respect to the molecular distances is examined. Compute D = f_xxf_yy - (f_xy)² and substitute (x,y) where it is the parameters for the stationary point. There is a saddle point if D is negative.

Trajectories from r₁ = r₂: locating the transition state:

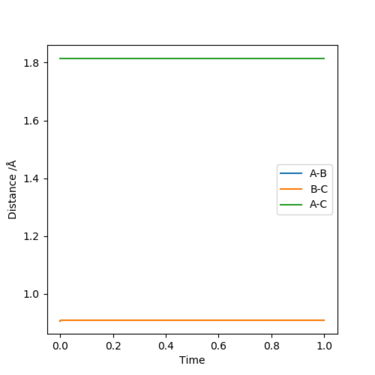
The best estimate of the transition state position was 0.9077421, it was found by minimising the forces to zero on the three H atoms. This estimate is good enough as they appear to be straight lines instead of sinusoidal functions.

Trajectories from r₁ = r_ts+ δ, r₂ = r_ts:

The conditions were set to r₁ = 0.9087421 and r₂ = 0.9077421:

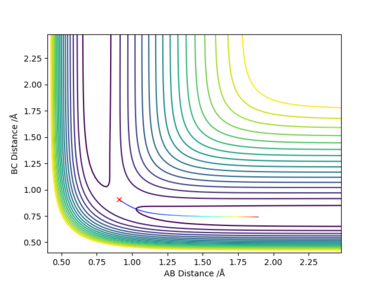
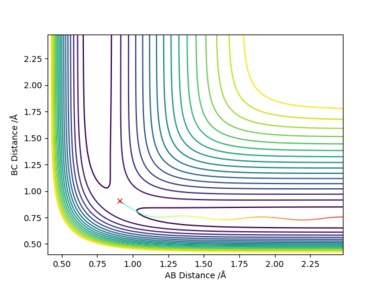
The difference between MEP and Dynamic reaction path is the absence of oscillatory motion in the MEP calculation. This is because the trajectory flows downhill along the minimum energy path at the transition state with all the inertia effects of the atoms removed.

If the values of r₁ and r₂ are reversed, the trajectory will be mirrored along the line x = y.

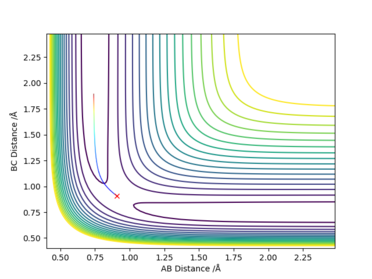
If the signs of the momenta are reversed, then the trajectory will approach very closely to the transition state but falls back and follow back the mirror image of the same trajectory. The time was set to be at 0.4 s.

AB distance	0.982206
BC distance	0.849663
AB momentum	-0.370287
BC momentum	0.205708

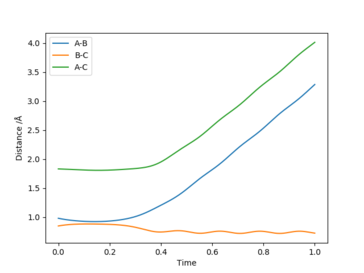
Reactive and unreactive trajectories:

The initial positions were set to be r₁ = 0.74 and r₂ = 2.0.

p₁	p₂	E_tot	Reactive?	Description of the dynamics
-1.25	-2.5	-99.018	Yes	H_A - H_B and H_C collide with weak oscillations. H_Bbreaks bond with H_A and forms bond with H_C. Some fluctuations of H_A - H_Bcan be seen.
-1.5	-2.0	-100.456	No	H_A - H_B and H_C gently collide with weak oscillation, but no reaction occurs. No bonds made or broken in the collision.
-1.5	-2.5	-98.956	Yes	H_A - H_B and H_C collide with weak oscillation. H_Bbreaks bond with H_A and form bond with H_C.H_B - H_c leaves with more oscillation.
-2.5	-5.0	-84.956	No	H_A - H_B and H_C collide with strong oscillations. H_Bbreaks bonds with H_A and bonds with H_C, H_B - H_c briefly forms but reverts back to H_A - H_Bas H_B breaks bond with H_C. H_A - H_B and H_C seperates with its original configuration.
-2.5	-5.2	-83.416	Yes	H_A-H_Bapproaches H_C violently (with strong oscillations). Collision between reactants causes initial successful reaction, but the strong oscillation leads to the break-down of the 'first products'. The 'first products' then reacts again to form H_A and H_B-H_C, hence overall reactive.

Conclusion from the table: A molecule with energy greater than its activation energy does not always lead to successful reactions . Specific trajectories, including initial momenta and separations are crucial for a successful reaction to occurs. This is shown in reaction 4 where the products are formed but then reform reactants.

Main assumptions of Transition State Theory:

Transition State Theory (TST) is a method for estimating rate constants of transitions. This method identify the dividing surface (transition state) that separates the reactants (initial state) and the products (final state). The assumptions are:

Once the system passes the transition state into the products, it does not return to the reactants.
The rate is slow enough that atoms in the reactant state have energies that are Boltzmann distributed.
Quantum tunneling effects are assumed negligible
Born-Oppenheimer approximation is introduced

As a conclusion, the reaction rates obtained using transition state theory would be higher than experimental values.

Exercise 2: F - H - H system

PES Inspection:

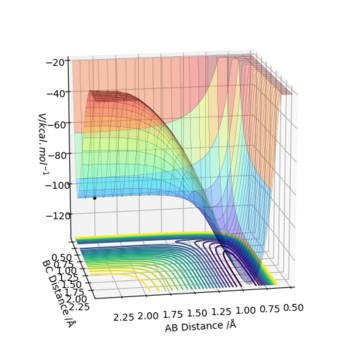
F + H₂ -> H + HF Exothermic as V_AB < V_BC

H + HF -> F + H₂Endothermic as V_AB > V_BC

From the PES plot, F + H₂ -> H + HF is an exothermic reaction as F and H₂ are located at higher potential energy surface. The H₂ molecule gains kinetic energy as it loses potential energy when H-H bond starts to break due to conservation of energy. The bond strength of H-F bond is 569 kJmol^-1 , which is higher than that of H-H bond of 432 kJmol^-1^[1]. The bond formed is of higher energy than the bond broken. Therefore, energy is released and the reaction is exothermic.

Transition state is at r_HF = 1.81025 and r_HH = 0.744891. Forces along H-F is -0.002 whilst along H-H is 0.000. Transition state total energy = -103.752 kcal/mol.

The Hammond's Postulate states that the transition state of a reaction resembles the structure of the species (reactant or product) to which it is closer in energy. Since F + H₂ -> H + HF is an exothermic reaction, the transition state should resemble its reactants (early TS).

Activation Energy F + H₂: -103.752 + 104.017 = +0.265 kcal/mol.

Activation Energy H + HF: -103.752 + 134.022 = +30.270 kcal/mol.

Reaction Dynamics:

Question 1:

The set of Initial conditions that results in a reactive trajectory are : r_FH = 2.0, r_HH = 0.74, p_FH = -0.9 and p_HH = -0.7

with E_tot = -101.928 kcal/mol

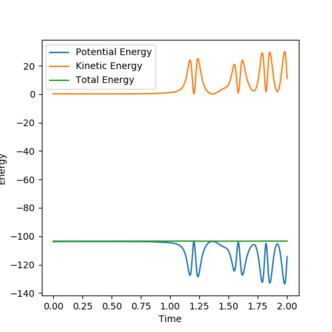
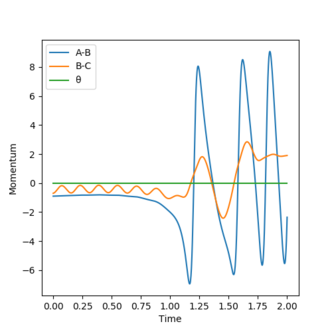
Initially, there is only little vibrational energy and the system is high in potential energy. As the reaction proceeds, there is an increase in the magnitude of momentum and average kinetic energy. The total energy of the system remains constant. This shows that there is an increase in vibrational energy in the HF molecule, which releases as heat in the system. This can be confirmed by performing the reaction and measuring the increase in temperature of the exothermic reaction using a bomb calorimeter.

Question 2:

For the reaction of F + H₂, with r_FH = 2.0, r_HH = 0.74, p_FH = -0.5 and p_HH between -3 and 3, the results of calculation can be shown in the table below (The step size was set to be 0.002):

p_HH	E_tot	Reactive?	Description of the dynamics
-3.00	-96.159	No	H_AH_B collides with F then rebounds back as H₂, leaving as H₂.
-2.95	-96.431	No	H_AH_B collides with F twice then rebounds back as H₂, leaving as H₂.
-2.90	-96.699	No	H_AH_B collides with F 4 times then rebounds back as H₂, leaving as H₂.
-2.85	-96.961	No	H_AH_B collides with F 3 times then rebounds back as H₂, leaving as H₂.
-2.80	-97.219	No	H_AH_B collides with F twice then rebounds back as H₂, leaving as H₂.
-2.70	-97.719	Yes	H_AH_B collides with F twice then rebounds back as H_B, forming HF as a product.
-2.60	-98.199	No	H_AH_B collides with F then rebounds back as H₂, leaving as H₂.
-2.50	-98.659	No	H_AH_B collides with F then rebounds back as H₂, leaving as H₂.
-2.00	-100.659	Yes	H_AH_B collides with F and rebounds back as H_B to form HF as a product.
-1.50	-102.159	Yes	H_AH_B collides with F 3 times and rebounds back as H_B to form HF as a product.
-1.00	-103.159	Yes	H_AH_B collides with F twice and rebounds back as H_B to form HF as a product.
0.00	-103.659	Yes	H_AH_B collides with F 3 times and rebounds back as H_B to form HF as a product.
+1.00	-102.159	No	H_AH_B collides with F twice and rebounds back as H₂.
+1.50	-100.659	Yes	H_AH_B collides with F and rebounds back as H_B to form HF as a product.
+2.00	-98.659	No	H_AH_B collides with F and rebounds back as H₂.
+2.50	-96.159	No	H_AH_B collides with F and rebounds back as H₂.
+2.60	-95.599	No	H_AH_B collides with F and rebounds back as H₂.
+2.70	-95.019	No	H_AH_B collides with F 3 times and rebounds back as H₂.
+2.80	-94.419	Yes	H_AH_B collides with F 9 times and rebounds back as H_B to form HF as a product.
+2.85	-94.111	Yes	H_AH_B collides with F 3 times then rebounds back as H_B, forming HF as a product.
+2.90	-93.799	Yes	H_AH_B collides with F twice and rebounds back as H_B to form HF as a product.
+2.95	-93.481	Yes	H_AH_B collides with F five times and rebounds back as H_B to form HF as a product.
+3.00	-93.159	No	H_AH_B collides with F and rebounds back as H₂.

From the table, it can be concluded that molecules having enough vibrational energy is not sufficient to lead to a successful reaction. The trajectory sometimes is still not able to go pass the transition state to form products even though it possess sufficient energy.

Question 3:

For the same initial positions (r_FH = 2.0, r_HH = 0.74), the momentum was increased slightly to p_FH = -0.8, and the overall energy of the system was considerably reduced by reducing the momentum p_HH = 0.1.

The total energy of the system is at -103.364 kcalmol^-1, which is very low. However, it still results in a successful reaction.

Reverse reaction, H + HF:

Case 1:

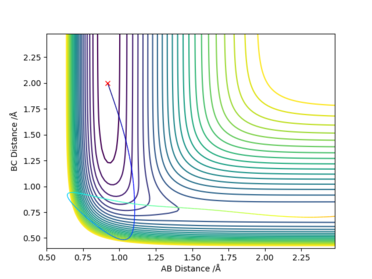
The initial conditions were set to be r_FH = 0.92, r_HH = 2.0, p_FH = -10.0 and p_HH = -16.0.

The total energy is +14.929 kcalmol^-1. The initial kinetic energy is +148.632 kcalmol^-1, which is way beyond the activation energy of 30.270 kcalmol^-1. As a result, the reaction is successful producing H₂. The majority of the KE stays on the single H atom, with only little vibration on the HF molecule.

Case 2:

Then, another calculation was performed with increased magnitude of momentum with the same initial positions (r_FH = 0.92, r_HH = 2.0). The initial momenta were set to be p_FH = -16.0 and p_HH = -16.0.

The total energy is + 1.034 kcalmol^-1. The initial kinetic energy is + 134.737 kcalmol^-1, which is still way beyond the activation energy. However, the reaction is unsuccessful.

Case 3:

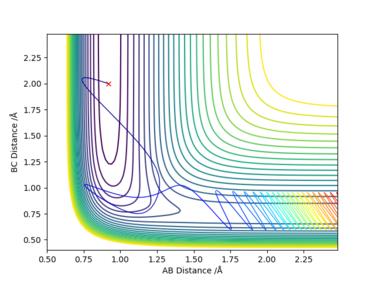
By trial and error (decreasing the momentum of the incoming H atom and increasing the vibrational energy of HF), a set of initial conditions is able to give produce a successful reaction with kinetic energy of +42.498 kcalmol^-1, which is much closer to the activation energy (~12 kcalmol^-1 difference). The set of initial conditions is: r_FH = 0.92, r_HH = 2.0, p_FH = -11.849 and p_HH = -4.0.

Also, the total energy of the system is - 91.204 kcalmol^-1, this is much lower than the previous system with total energy of + 1.034 kcalmol^-1.

Polanyi's empirical rules

Definition:

The Polanyi's empirical rules^[2] state that vibrational energy is more efficient than translational energy in activating late-barrier reactions (endothermic reactions), whereas the reverse is true for an early-barrier reactions (exothermic reactions). The distribution of energy between varied modes, including translational and vibrational modes, will affect the efficiency of the reaction.

Illustration of Polanyi's empirical rules:

Illustration of Polanyi's empirical rules in the above two cases of H₂ + F (exothermic) and H + HF (endothermic):

For F and H₂, it has been illustrated that having sufficient kinetic energy without an excess of vibrational energy results in a reactive trajectory. The reaction results in an unreactive trajectory if the system has a low kinetic energy and a high vibrational energy. Therefore, translational energy is more efficient than vibrational energy in activating exothermic reactions.

For H + HF, it has been illustrated that having sufficient vibrational energy without an excess of kinetic energy results in a reactive trajectory. The reaction results in an unreactive trajectory if the system has a low vibrational energy and a high kinetic energy. Therefore, vibrational energy is more efficient than translational energy in activating endothermic reactions.

In conclusion, by Hammond's postulate, the computer simulations suggest that kinetic energy is more efficient than vibrational energy in exothermic reactions as they have early transition states. On the other hand, vibrational energy is more efficient than kinetic energy in endothermic reactions as they have late transition states

References

↑ http://www.wiredchemist.com/chemistry/data/bond_energies_lengths.html
↑ https://www.chemistryviews.org/details/news/1378289/New_Rules_for_Reaction_Dynamics.html

[1] ttp://www.wiredchemist.com/chemistry/data/bond_energies_lengths.html

[2] ttps://www.chemistryviews.org/details/news/1378289/New_Rules_for_Reaction_Dynamics.html

[1]

[2]

Exercise 1: H + H2 system