MRD:ds3817 cp3md
H + H2 system
Stationary points of potential energy occur where Vr1 = 0, Vr2 = 0 simultaneously.
Let the coordinates of the equilibrium be at (a, b), evaluate: D = [Vr1r1Vr2r2− (Vr1r2)2]a.b .
If D > 0 and Vr1r1(a, b) < 0, then (a, b) is a maximum;
If D > 0 and Vr2r2(a, b) > 0, then (a, b) is a minimum;
If D < 0, then (a, b) is a saddle-point.
I know what you mean by your mathematical explanation, but it is not entirely easy to follow/correct. Perhaps start off with writing the derivative out clearly because typing evaluate D does not tell us how to do this, wherease a partial differential will. So what does all this information tell us about the TS and a saddle point? What is the relevance of a minimum and a maximum to the TS? Mys18 (talk) 15:33, 19 May 2019 (BST)
Reaction Path
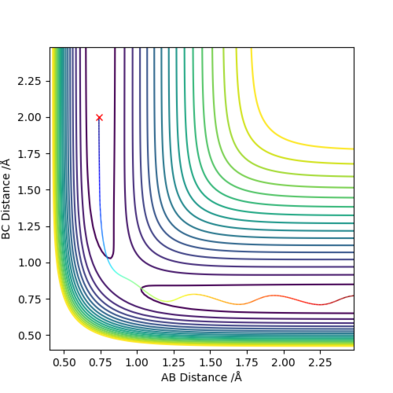
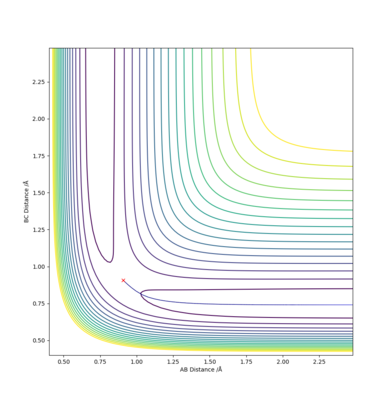
Trajectories from r1 = r2: Locating the transition state
My best estimate of the saddle-point (transition state position, rts) is 0.9077421 Å, which was found by minimising the force on the 3 H atoms.
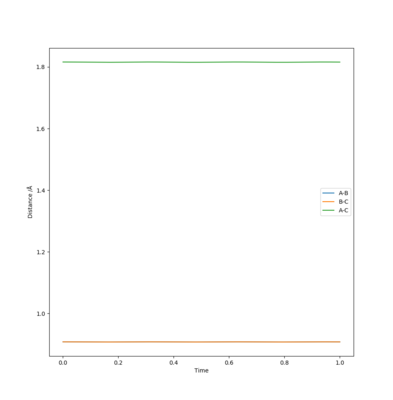
Great and nicely remembered to include units. Double check how many decimals your value should be quoted to... Mys18 (talk) 15:36, 19 May 2019 (BST)
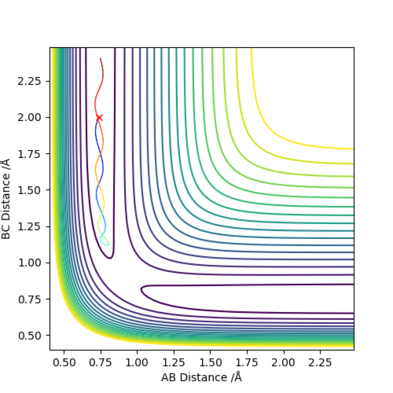
Reaction Path: Trajectories from r1 = rts+δ, r2 = rts
With conditions r1 = 0.9077422 Å and r2 = 0.9077421 Å:
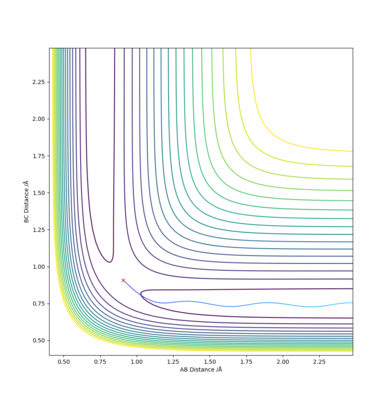
MEP calculations do not take in account vibrations of the molecules as it only stays at the bottom of the valley without oscillations, while dynamic calculations takes in account the vibration of the molecule.
Good, why does the MEP method not take vibrational motions into account? Mys18 (talk) 16:17, 19 May 2019 (BST)
If r1 and r2 are reversed, then the trajectory will be mirrored along y=x.
If the signs of the momenta are reversed, then the trajectory will approach the transition state but falls back and return in the same trajectory.
| AB distance | 1.8744768230045634 |
| BC distance | 0.7543850270962071 |
| AB momentum | -2.3688869147584435 |
| BC momentum | -1.2835267769280745 |
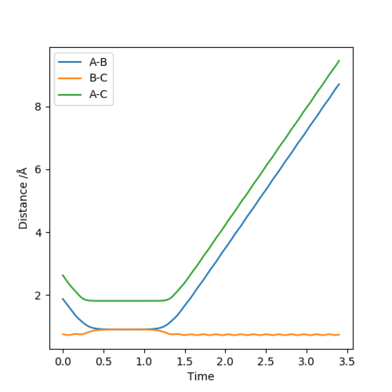
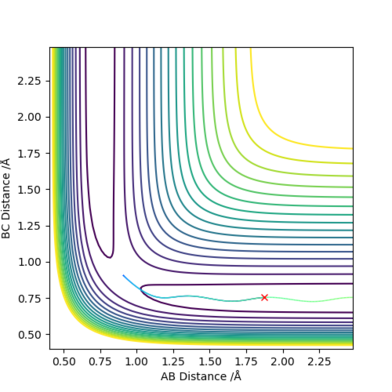
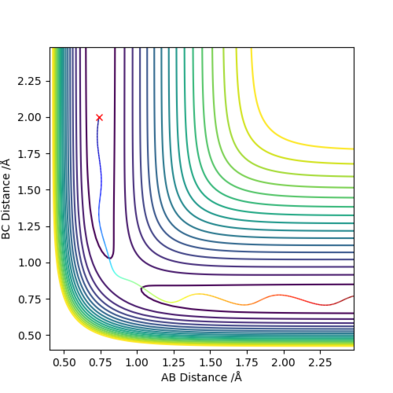
Reactive and unreactive trajectories
With initial positions r1 = 0.74 and r2 = 2.0:
| p1 | p2 | Etot | Reactive? | Description of the dynamics | Trajectory |
|---|---|---|---|---|---|
| -1.25 | -2.5 | -99.018 | Yes | HA-HB collides with HC gently (with weak oscillations) and reacts to form HA and HB-HC. HB-HC leaves with stronger oscillation than the initial HA-HB molecule. |  |
| -1.5 | -2.0 | -100.456 | No | HA-HB collides with HC gently (with weak oscillations) but does not react. No bonds were broken or made in this collision. |  |
| -1.5 | -2.5 | -98.956 | Yes | HA-HB collides with HC gently (with weak oscillations) and reacts to form HA and HB-HC. HB-HC leaves with stronger oscillation than the initial HA-HB molecule. |  |
| -2.5 | -5.0 | -84.956 | No | HA-HB collides with HC violently (with strong oscillations), collision causes initial successful reaction, but the strong oscillation results in the break-down of the product, reverting back to the sets of molecules in the initial conditions, hence overall unreactive (oscillating between transition states but ends up unreactive). |  |
| -2.5 | -5.2 | -83.416 | Yes | HA-HB approaches HC violently (with strong oscillations), collision causes initial successful reaction, but the strong oscillation leads to the break-down of the 'first products'. The 'first products' then reacts again to form HA and HB-HC, hence overall reactive (oscillating between transition states and ends up reactive). |  |
Conclusion: Reaching activation energy in a reaction does not necessarily mean all trajectories will result in a successful reaction, specific trajectories (i.e. initial momentum and separation) is also important for a successful collision (reactive trajectory).
Precisely, as these is seen for Reaction 4 where we form products but then reform reactants.. Mys18 (talk) 16:21, 19 May 2019 (BST)
Main assumptions of Transition State Theory:[1]
- Once the system reaches the transition state, with a velocity towards the product configuration, it will not reenter the initial state region. (This is the most important approximation because it leads to severe constraints on where a transition state can be chosen).
- Atoms in the reactant state have energies that are Boltzmann distributed. (This should be satisfied if the system has had enough time to thermally equilibrate).
- Quantum-tunneling effects are assumed negligible.
- Born-Oppenheimer approximation is invoked.
Predictions using Transition State Theory: The rate of reaction will be increased under the prediction of TST as once the reactants have gone past TS, it will not reenter the initial state.
Excellent and clearly explained assumptions! Mys18 (talk) 16:21, 19 May 2019 (BST)
F - H - H system
PES Inspection
F + H2: Exothermic, because VAB < VBC
H + HF: Endothermic, because VBC > VAB
Perhaps write out F + H2 AND H + HF -> Mys18 (talk) 16:23, 19 May 2019 (BST)
This implies that the H-F bond is more stable, stronger than the H-H bond.
From your knowledge of bonding why is the H-F bond strong? Would be nice to see energy values for bond forming/breaking which also gives an insight to whether the reaction is endo/exo. Mys18 (talk) 16:25, 19 May 2019 (BST)
The approximate position of the transition state is 1.810753 Å, 0.7448787 Å.
Activation Energy F + H2: -103.752 + 104.017 = +0.265 kcal/mol.
Activation Energy H + HF: -103.752 + 134.022 = +30.270 kcal/mol.
Great job on the units. Mys18 (talk) 16:26, 19 May 2019 (BST)
Reaction Dynamics
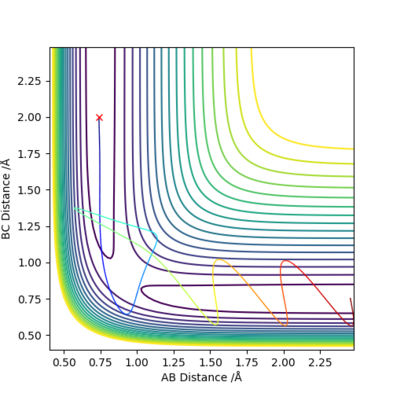
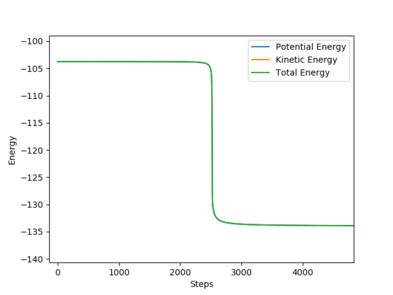
One set of Initial conditions that results in a reactive trajectory: rFH = 2.0, rHH = 0.75, pFH = -1.0 and pHH = -1.75
with Etot = -101.928 kcal/mol
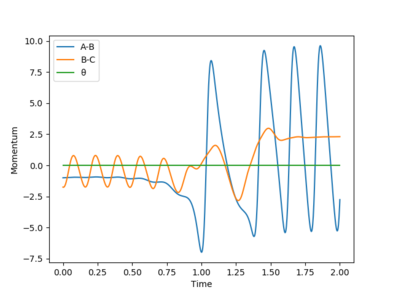
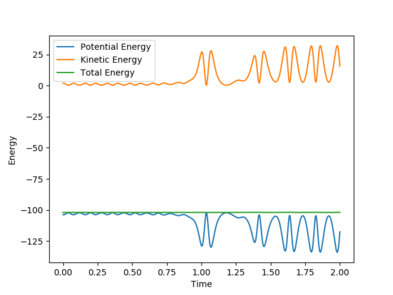
As the reaction progresses, potential energy is converted to kinetic energy and ultimately into heat energy (increased vibration of bonds). The momentum of the system also increases while the total energy remains constant as the reaction progresses. This can be confirmed by performing the reaction and measuring the increase in temperature of the exothermic reaction using a bomb calorimeter.
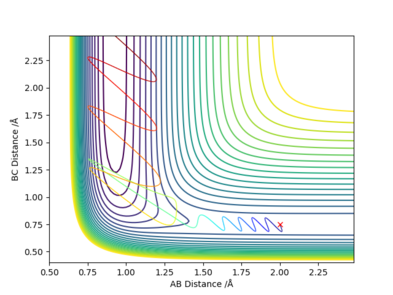
Results of calculations with rFH = 2.0, rHH = 0.74, pFH = -0.5 and pHH between -3 and 3 can be shown in the table below (step size as 0.002).
| pHH | Etot | Reactive? | Description of the dynamics |
|---|---|---|---|
| -3.00 | -96.159 | N | HAHB collides with F one time and rebounds back as H2. |
| -2.90 | -96.699 | N | HAHB collides with F four times and rebounds back as H2. |
| -2.80 | -97.219 | N | HAHB collides with F two times and rebounds back as H2. |
| -2.70 | -97.719 | Y | HAHB collides with F two times and rebounds back as HB to form HF as a product. |
| -2.60 | -98.199 | N | HAHB collides with F one time and rebounds back as H2. |
| -2.50 | -98.659 | N | HAHB collides with F one time and rebounds back as H2. |
| -2.00 | -100.659 | Y | HAHB collides with F one time and rebounds back as HB to form HF as a product. |
| -1.50 | -102.159 | Y | HAHB collides with F three times and rebounds back as HB to form HF as a product. |
| -1.00 | -103.159 | Y | HAHB collides with F two times and rebounds back as HB to form HF as a product. |
| 0.00 | -103.659 | Y | HAHB collides with F three times and rebounds back as HB to form HF as a product. |
| +1.00 | -102.159 | N | HAHB collides with F two times and rebounds back as H2. |
| +1.50 | -100.659 | Y | HAHB collides with F one time and rebounds back as HB to form HF as a product. |
| +2.00 | -98.659 | N | HAHB collides with F one time and rebounds back as H2. |
| +2.50 | -96.159 | N | HAHB collides with F one time and rebounds back as H2. |
| +2.60 | -95.599 | N | HAHB collides with F one time and rebounds back as H2. |
| +2.70 | -95.019 | N | HAHB collides with F three times and rebounds back as H2. |
| +2.80 | -94.419 | Y | HAHB collides with F nine times and rebounds back as HB to form HF as a product. |
| +2.90 | -93.799 | Y | HAHB collides with F two times and rebounds back as HB to form HF as a product. |
| +3.00 | -93.159 | N | HAHB collides with F one time and rebounds back as H2. |
Again, we can see that having sufficient vibrational energy does not necessarily result in a successful reaction. The trajectory might still be unable to go pass the transition state despite the vibrational energy being a lot bigger of the activation energy.
For the same initial position, HAHB collides with F two times and rebounds back as HB to form HF as a product despite a slight increase in the momentum pFH = -0.8 and a reduction in the overall energy of the system by reducing the momentum pHH = 0.1.
A calculation was performed with rFH = 2.0, rHH = 0.74, pFH = -0.8 and pHH = 0.1. The total energy is -103.364 kcal/mol, which was enough to go over the transition state.
Consider the reverse reaction, H + HF:
A calculation was performed with rFH = 0.92, rHH = 2.0, pFH = -9.0 and pHH = -15.0. The total energy was -1.071 kcal/mol, with initial kinetic energy +132.632 kcal/mol, beyond the required activation energy, resulting in a successful reaction producing H2.
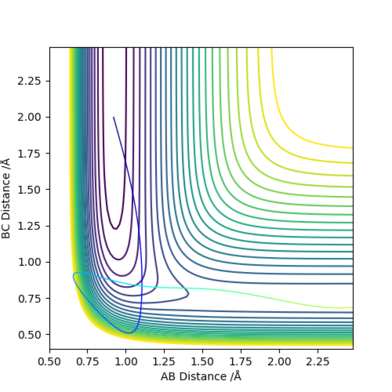
However, when the calculation was performed with increased magnitude of momentum rFH = 0.92, rHH = 2.0, pFH = -15.0 and pHH = -15.0, the total energy was -15.281 kcal/mol, with initial kinetic energy +118.421 kcal/mol, still far beyond the required activation energy, resulted in an unsuccessful reaction.
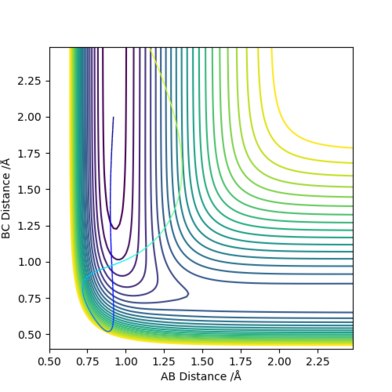
By decreasing the momentum of the incoming H atom and increasing the energy of the H - F vibration, a reactive trajectory was obtained with set of conditions with rFH = 0.92, rHH = 2.0, pFH = -11.85 and pHH = -4.00 with an initial kinetic energy of +42.507 kcal/mol, which is significantly lower than the previous kinetic energy of +118.421 kcal/mol. This set of conditions also had a total energy of -91.196 kcal/mol, which is also significantly lower than the previous total energy -15.281 kcal/mol.
Nice mentioning of the temperature and also vibration of bonds, so besides what you have already mentioned what else could be experimentally used? Mys18 (talk) 16:31, 19 May 2019 (BST)
The distribution of energy between different modes (translation and vibration) will affect the efficiency of the reaction, and is influenced by the position of the transition state. Polanyi's rules[2] states that vibrational energy is more efficient in promoting a late-barrier reaction than translational energy (better for endothermic reactions). Conversely, kinetic (translational) energy is more efficient in promoting an early-barrier reaction than vibrational energy (better for exothermic reactions).
By the exothermic reaction between F and H2, it is shown that having enough kinetic energy (i.e. just above the energy of transition state) without an excess in vibrational energy is able to result in a reactive trajectory but results in an unreactive trajectory when the system has a lower kinetic energy and a high vibrational energy.
Contrasting with the endothermic reaction between HF and H, it is shown that having enough more vibrational energy without an excess in kinetic energy (hence a lower total energy) is more practical than having a low vibration energy and a large excess of kinetic energy (hence a much higher total energy) in producing a reactive trajectory.
These computer simulations along with Hammond's postulate suggests that kinetic energy is more effective than vibrational energy in exothermic reactions (when the transition state resembles the reactants) and vice versa for endothermic reactions (when the transition state resembles the products), supporting Polanyi's rules.
Excellent! Nice to see you have not simply stated Polanyi's rules, but rather related it to your findings. Overall good work, despite some initial corrections, your answers have been clear and very well explained. Your figures have been complimented with the correct units which is not always seen! Good job :) Mys18 (talk) 16:36, 19 May 2019 (BST)