User:Ca307/Mod1:81036pba

Section 1: Modelling using Molecular Mechanics

1.1 Hydrogenation of Cyclopentadiene Dimer

Fig.1 Dimerisation of cyclopentadiene

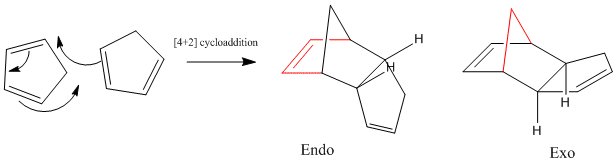
Cyclpentadiene dimerises via a Diels-Alder 4π_s + 2π_s cycloaddition to give the endo product (2). Calculations run, based on molecular mechanics (MM2 force field), indicate that the endo product is thermodynamically less stable than the alternative exo product (1) (Table 1). The stretching, bending and van der Waals components of this total energy are approximately equal for both. The energy difference is largely due to increased torsional strain of the endo conformation (Tor contribution = 9.51 kcalmol^-1 for endo vs. 7.3 kcalmol^-1 for exo). This is likely to be due to increased steric hindrance on going from exo to endo,a result of changing the carbon bridge (shown in red Fig.1.)that eclipses the 5 membered ring. .

Fig.2 Dihydro derivatives of 2

Table 1. Relative eneregies of products as calculated using MM2 minimisation

Product	Total Energy/kcalmol-1
1	31.89
2	33.99
3	35.70
4	31.15

Fig.3. FMOs of interacting cyclopentadiene molecules to give endo selectivity

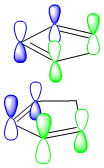
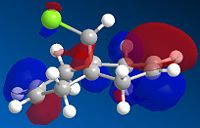
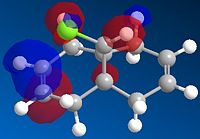
The formation of the endo product is therefore, the kinetically favoured outcome ie. the product formed when the reaction is under irreversible conditions. In order to explain this 'endo selectivity' for Diels-Alder reactions, consideration of the frontier molecular orbitals proves useful. Primary orbital interactions (shown in green Fig.3) result in bond formation, whilst secondary orbital interactions (shown in blue Fig.3) result in the obsereved stereoelectronic outcome. This favourable secondary interaction results in a lower energy pathway for endo product formation.

Dihydrogenation of endo product (2) can occur either at the double bond in the 5 membered ring (to give product 3) or at the double bond in the norborene ring (yielding product 4)(Fig.2). MM2 minimisation reveals that dihydrogenated product 4 is thermodynamically favourable realtive to 2, whilst also indicating that formation of 3 would be unfavourable thermodynamically. The relative energy contributions to the energy difference between the dihydrogenated products (Table 2) shows that it is largely due to torsional and bending contributions. On going from parent product 2 to either 3 or 4, there is a decrease in bending contribution (bend. contribution for 2 = 20.6 kcalmol^-1)whilst there is an increase in torsional strain (increased steric hindrance on going from sp² to sp³ and larger for 4 due to eclipsed nature of H interactions with ring junction H -smaller ring therefore sterically more constrained)(Fig. 4a and 4b).

Fig.4a Demonstrating H torsional interaction in 3

Fig.4b Demonstrating torsional interactions in 4

Table 2. Contributions to total energy/ kcalmol^-1

Energy component	Product 3	Product 4
Stretch	1.28	1.10
Bend.	19.98	14.51
Torsion	10.71	12.49
1,4 vdW	5.64	4.51
H-Bond	N/A	N/A

However, it is largely the lower bending energy of 4 that makes it thermodynamically favourable (in comparison to the bending energy of the parent product it can be seen that the double. By consideration of the dihedral angles (Table.3.) within the rings conatining the doule bond in 3 and 4 the energy difference can be explained (with use of the equation for bending/angle energy: U = k(θ-θ_eq)², where θ_eq is the eqilibrium dihedral angle[1]. Hence, large deviations from this value result in higher energy).

Table.3. Comparison of internal bond angles

Ring	Ideal internal angle°	Average measured angle°
6-mem in 3	120	107.8
5- mem in 4	108	106.5

The average dihedral angle in the 5-mem ring of 4 is almost at it's ideal, minimum energy value, whilst the average measured value for the 6-mem ring in 3 reveal it to have a significant degree of distortion from it's preferred equilibrium angle.

1.2 Stereochemistry of Nucleophilic additions to a pyridinium ring (NAD⁺ analogue)

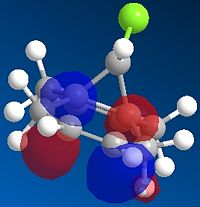
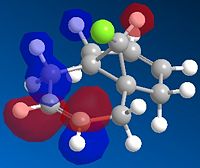
Nucleophilic addition of the Grignard reagent MeMgI to reagent 5 results, with very high stereoselectivity, in formation of product 6. Shultz et al. suggest that due to limited flexibility of the seven membered ring, 5 can only adopt two feasible minimum energy conformations - one with the carbonyl above the plane of the pyridinium ring (anti to hydrogen at chiral centre marked with * Fig.5) or with carbonyl co-planar to the pyridinium ring. Hence, chelation of the Grignard to the oxygen of the carbonyl results in addtion of the methyl group to the C4 position of the pyridinium ring on the same face as the carbonyl.

Fig.5 Nucleophilic addition of Grignard reagent-showing chelation in first step

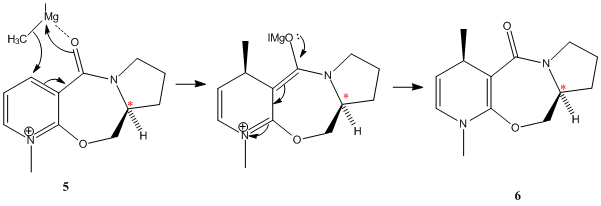
Energy minimisation calculations using the MMFF94 force field have been used to try to investigate this. N.B the Grignard cannot be included in the energy minimisation as molecular mechanics is unable to deal with metal atoms.

Table.4. Results of energy minimisation of Reagent 5

Conformation	Dihedral angle/o	Energy /kcalmol-1	Comment
1	8	57.39	Lowest energy conformation. Carbonyl anti to chiral H.
2	-4	57.52	Carbonyl nearly co-planar.
3	27	60.90	Carbonyl above plane. Molecule distorted from planar conformation.
4	-11	289.1	Carbonyl below ring and syn to chiral H. High energy - not realistically an energy minimum

The initial optimisation led to the lowest energy conformation with the carbonyl slightly above the plane of the ring. Further optimisations from varying initial starting conformations, with small distortions of either the 5 membered ring, 7 membered ring or carbonyl position consistantly led to this low energy conformation (~57 kcalmol^-1). It was possible to decrease the dihedral angle slightly, so the carbonyl adopts an almost planar conformation, at a small energy cost. Forcing the carbonyl to adopt a conformation above the pyridinium ring with a larger dihedral angle was possible, with the twisting of the molecule away from a fairly linear conformation likely to be responsible for the energy increase. These results would indicate that chelation of the Grignard to the carbonyl of the molecule would result in the delivering of the methyl group to the top face (ie. directed to the same face as carbonyl). Attempts to force the carbonyl below the plane of the ring, to be syn with the H at the indicated chiral centre, resulted in formation of a high energy species that cannot realistically be considered as an energy minimum, also in accordance with Shultz (ie. there are only 2 possible energy minimum conformations).

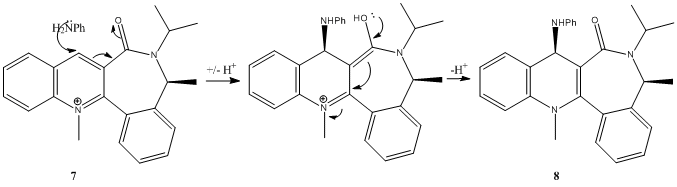
In contrast, nucleophilic attack of H₂NPh on reactant 7 results in the formaton of a product that has the new group attatched to the opposite face to the carbonyl -MMFF94 optimisation having revealed that the minimum energy conformation of 7 has the carbonyl below the plane of the ring.

Fig.6 Nucleophilic addition to reactant 7

l

Table 5. Relative energies of confromations of 7

Dihedral angle/o	Energy/ kcalmol-1	Comment
-38	99.51	Angle larger than optimum - energy higher
-37	98.26	Lowest energy conformation - optimum dihedral angle.
-34	101.70	Angle smaller than optimum - energy higher
0	934.73	Not realistically possible - methyl group is protuding through the aromatic ring

Many starting conformations were used in an attempt to force the carbonyl above the plane of the ring. The closest that was achieved was having the carbonyl co planar with the aromatic system,at such a high energy that it is clearly not realistically feasible. The results suggest that there is very little conformational freedom along the C3(pyridinium)C=O bond (labelled as a chiral axis by Leleau et. al.), possibly resulting in the atropisomerism alluded to in the lab script.

Since the carbonyl clearly prefers to stay positioned on one side of the ring system, the electron rich incoming nucleophile (H₂NPh) will attack the opposite face to avoid unfavourable electronic interactions with the oxygen of the carbonyl group, resulting in the stereochemical outcome shown.

The MM approach can be used to give an understanding of likely thermodynamic outcomes, but to gain a full undersatnding of the reaction, in particular the kinetic outcome, information about the transition state would need to be known. This is not possible to obtain form MM, requiring consideration of MO theory and a model that is more quantum mechanical in nature.

1.3 Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

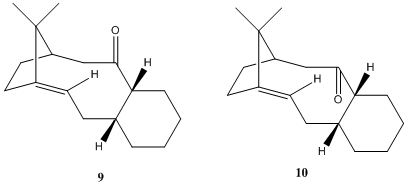
9 and 10 are atropisomers (due to restricted rotation about C-C=O bonds) of an intermediate in the synthesis of Taxol. Although one isomer is initially formed, it will isomerise to the other upon standing. MM2 enrgy optimisations of several conformations of both isomers have been run to try to rationalise the relative stabilities (Table.6.).

Initial optimisations, regardless of the 2D input structure, consistently gave isomer 10, with the cyclohexane in a chair conformation. Manual distortion followed again by optimisation eventually yielded isomer 9, initially with a twist boat conformation of the 6 member ring. In both cases it was possible to manipulate the molecule to adopt conformations with the 6 member ring in the alternative conformation. As would be expected, structures with cyclohexane in chair conformations are lower in energy than the corresponding twist boat. Manual manipulation is requred, as the optimisation tends to find the local minima and not necessarily the global minimum. However, Elmore and Paquette seem to indicate that the bridge in 9 does fix it in the higher energy conformation. Hence, from this it can be suggested that 9 will likely undergo isomerisation to the thermodynamically more stable 10 (with cyclohexane in the chair conformation). Therefore, any addition to the carbonyl of this intermediate is likely to occur along the Burgi -Dunitz angle, from the top face of the molecule (with the carbonyl 'down', below the plane).

Optimisation using the MMFF94 force field on pre MM2 optimised molecules gave similar results - again indicating that structures with cyclohexane in the more stable chair conformation are lower in energy, and also concluding that isomer 10 is thermodynamically more stable. MMFF94 optimisation without prior MM2 minimisation also led to the initial formation of 10 (with cyclohexane chair). However, it also proved easier to change the relative positions of the carbonyl, without optimisation back to 10, albeit initially to a higher energy local minima of 9 (eg. E= 82.62 kcal^mol-1).

Further optimisations led to the results already obtained.

Fig. 7 Intermediate in the formation of Taxol - atropisomers

Table.6. Relative energies of isomers 9 and 10using MM2 minimisation

Isomer	Cyclohexane conformation	Energy/kcalmol-1
10	Chair	44.32
10	Twist boat	49.87
9	Chair	48.90
9	Twist boat	54.14

Table.7. Relative energies of isomers 9 and 10 using MMFF94 minimisation (on previously MM2 minimised structures)

Isomer	Cyclohexane conformation	Energy /kcalmol-1
10	Chair	60.54
10	Twist boat	68.87
9	Chair	70.52
9	Twist boat	77.88

Reactivity of the Bridgehead Alkene

Despite Bredt's rule, stating that elimination towards a bridgehead is not observed, due to strain in formation of an sp² carbon at a bridgehead,in larger ring systems (as is the case here, with 9/10 containing a 10 member ring), bridgehead olefins can be isolated. Furthermore, it has now been shown that in certain cases the olefin is actually more stable than the parent alkane. These alkenes are termed 'Hyperstale olefins', and exhibit reduced reactivity to what would be expected. ie. lower values for enthalpy of hydrogenation. Maier and Schleyer suggest that the unrecativity of these hyperstable alkenes is due to the fact that the cage structure adds 'special' stability to the olefin and that on going from sp² to the sp³ parent alkane would result in increased strain ie. hyperstable olefins have negative olefin strain energies.

Hence, this is likely to be the cause of the slow observed reactivity of the alkene in the above intermediate. One way to verify this would be to compare the relative energy of the most stable conformation of 10 with its parent alkane (10b). Upon MM2 minimisation, the energy was found to be 53.07 kcalmol^-1 - higher than that of 10, as would be predicted.

Section 2. Modelling Using Semi-empirical Molecular Orbital Theory

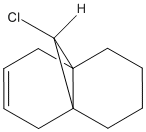
2.1 Regioselective Addition of Dichlorocarbene

Use of the MOPAC/PM6 method to approximate the molecular wavefunctions of 12 (Fig.8) can be used to predict the outcome of reactions with electrophiles (ie. dichlorocarbene). Consideration of the calculated MOs allows for the prediction of the most nucleophilic double bond (ie. most likely site of electrophilic addition).

Fig.8 Reactant 12

The results (Table. 8) reveal that the HOMO of 12 is laregly localised on the endo double bond - making this the most likely site of electrophilic adddtion. As to why the endo alkene is more nucleophilic than the exo alkene, can be explained by consideration of the other MOs of 12 and the relative positioning of the orbitals. In particular, the C-Cl σ^* orbital is positioned correctly for interation with the п orbital of the exo alkene. Hence, this stabilising interaction results in lowering the energy of the exo п orbital, relative to the corresponding endo orbital, (ie. it is now the HOMO-1 and shows a greater amount of delocalisation) and also removal of electron density away from this double bond.

Orbital interations involved in addtion reaction with CCl₂: 1. π_C=C (endo - HOMO of 12) → p_vac

2.n_C→ π^*_C=C (endo-LUMO+2 of 12)

Table. 8. Relelvant Molecular Orbitals of 12

MO	HOMO-1	HOMO	LUMO	LUMO +1	LUMO + 2
Comment	Significnat amount of electron density localised at the exo double bond ie.exo п orbital	Electron density largely localised on endo double bond - making this more nucleophilic ie.endo п orbital	~ exo п* based MO	Cl-C σ* - correct polarity and alignment for interaction with the exo п orbital (HOMO-1)	~ endo п* based MO

2.2 Stretching frequencies

One way to provide further evidence for the interaction of the exo п orbital with the C-Cl σ^* orbital is to analyse the C=C and C-Cl stretching frequencies both of 12, and when the exo double bond is removed, 12b. A study of the calculated stretching frequencies (Table.9.) indicates that the exo alkene C=C bond is weaker than the endo equivalent. Hence, supporting the conclusion drawn above; that electron density is being removed from the exo double bond by way of interaction with the C-Cl σ^* orbital. Furthermore, on going from 12 to 12b there is an increase in C-Cl bond strength - a result of less electron density in the C-Cl antibonding orbital, due to there not being an exo π system to interact with and also confirming the conclusion that it is the C-Cl σ* orbital that is accepting electron density from the exo double bond.

Fig.9 Molecule 12b- dihydro derivative of 12

Table 9. Relative Stretching Frequencies/ cm^-1

Bond	12	12b
endo C=C	1757.4	1758.0
exo C=C	1737.1	N/A
C-Cl	770.9	774.9

It is therefore reasonable to predict that by adjusting the nature of the substituents on the exo alkene, the stretching frequency of the C-Cl bond could be attenuated. It would be expected that by increasing the electron density on the exo alkene (in π orbital, as judged by the exo C=C stretch freq.) that this would result in increased electron donation into the C-Cl σ^*,thus reducing the stretching frequency of this bond. In contrast, the introduction of a EWG would have the opposite effect,ie. increase the C-Cl stretching frequency through removal of electron density from the alkene (and decrease the C=C stretch freq.). Indeed, for simple cases, OH (EDG) and CN (EWG)this is what is observed (Table.10.).

For the case with BH₂ and SiH₃ substituents it becomes slightly harder to analyse. BRH₂ being electron deficient can accept electron density into it's empty p orbital (Lewis Acid). Therefore, the introduction of two of these EWGs onto the alkene was expected to show a marked decrease in C=C frequency and a corresponding increse in C-Cl stretch frequency. However, although the decrease in the C=C stretch freq. is observed, there is also an unexpected decrease in the C-Cl freq., in comparison to 12. A similar argument was also proposed to predict the outcome of the introduction of 2 x SiH₃ subtituents. SiX₄, having the ability to 'expand the octet' has the potential to accept electron density from the alkene through overplap of an appropriate d-orbital with the π orbital. As with the BH₂ case, there is a significant decrease in C=C stretching frequency, abeit not as great as for the previous case. This can probably be explained by the relative sizes of the orbital involved eg. there is a better overlap between the alkene π orbital and the boron p orbital than with the silicon 3d orbital.

How can the decrease in C-Cl stretching frequency for these two cases be explained? There has been no direct change of mass of the atoms involved, therefore the change must be related to a decrease in the bond strength - a result of increased electron occupation of the Cl-C antibonding orbital, through better interaction with an occupied orbital. Attemps to qualify this through studying the potential MOs is inconclusive (Table.10.). Although the HOMO-1 orbital of the SiH₃ case is very similar to that already seen, the LUMO + 1 (and LUMO +2) is very diffuse - possibly resulting in greater overlap with the HOMO-1, but not necessarly localising electron density into the C-Cl antibonding orbital. In contrast the LUMO+2 orbital for the 2x BH₂ case resebles the C-Clσ^*, but the HOMO-1 is more distorted.

Table.10. Stretching frequencies/cm^-1 for 12 with change in substituents on the exo alkene,

Substituent	exo C=C	endo C=C	C-Cl
2 x OH	1797.54	1757.65	758.81
2 x CN	1670.40	1757.131	772.64
2 x BH2	1604.44	1758.2	761.48
2 x SiH3	1633.82	1754.90	767.94

MOs of interest

2 x BH2	2 x SiH3
HOMO-1	LUMO+1
	Very diffuse

Mini Project:Stereoselective Synthesis of Aspergillide A

Introduction

Aspergillide A and B are naturally derived 14-membered ring macrolides. The first successful synthesis of aspergillide A, with the correctly assigned structure, 1, was reported at the end of 2009 . Earlier in 2009 a synthesis of structure 2, believing this to then be aspergillide A was proposed. Only after full spectroscopic analysis was it found that structure 2 actually corrersponds to Aspergillide B, reviving the search for the correct structure of A.

Fig.10. Structure aspergillide A and the relevent isomers. Optimised geometry Jmols:

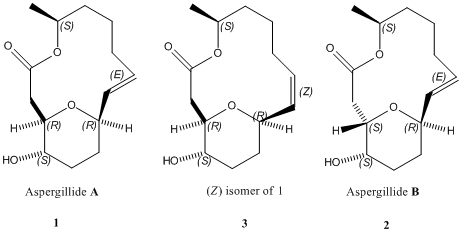
The synthesis of A, involves a stereoselective ring closing metathesis (RCM), giving exclusively the (Z) alkene isomer, 4a ,rather than the expected mix of isomers, 4a and 4b. Molecular mechanics was actually used by Diaz-Oltra et al. to gain some insight into this remarkably high selectivity, given the size of the ring formed. Their PM3 calulaions revealed the (Z) isomer 4a to be thermodynamically more stable than 4b. However, although they state that it is possible that the RCM is under thermodynamic control, it may also be plausible that the formation of the (E) isomer is also kinetically unfavoured - a result of possible conformational restraint imposed by the tetrahydropyran entity.

It proved difficult to cleave the benzyl oxygen bond in 4b (to give 1), hence the need for the introduction of 3, the (Z) isomer of 1, into the synthesis. Upon photoisomersation of the alkene in 3, the desired product (56%), Aspergillide A was formed and later separated from 3 via column chromatography.

Being able to use spectospopic techniques to differentiate between isomers proved to be a key point in the identification of the correct structure of Aspergillide A. The molecular models(see Jmols in Fig.10) help to show that changing the configuration at one stereocentre on going from 1 to 2, has a significant impact on the structural conformation. Hence, both the ¹³C NMR data and ¹H NMR data are sufficiently different for these isomers to allow for identification.eg. both the calculated and experimental values show a notable change in shift for C1(centre at which relative stereochemistry has been changed) and C15 (Fig.12 for numbering). Furthermore, as noted by Hande et al. , the use of optical rotation was also helpful. However, although this may be a useful technique in the lab, as the rotation values are under 100°, the computational techniques available here are not sufficient to be able to calculate them for comparison within a reasonable degree of accuracy.

In terms of being able to distinguish between 1 and 3, ie. differentiating between a cis or a trans alkene, ³J_HH coupling constants (using the Karplus equation) should be particulary useful. However, the suggested way of doing this (Haasnoot model [2], does not seem to include an option for alkenes.

Only the carbonyl and hydroxy group IR stretches are reported , showing only minor differences. IR analysis of all the molecules was run, in part to see why C=C stretches are not reported. The calculated values show significant deviations from lit.values, and do not provide a successful way of distinguishing between the isomers eg. for A (1), lit C=O: 1724cm^-1 vs. calc C=O: 1826cm^-1. This is possibly due to the vibrations being calculated in a different medium (ie. in the gas phase) to the experimental nujol mull.

>Can computational methods be used to predict the spectral properties to allow Apergillide A (1) to be distinguished from it's isomers Aspergillide B (2) and 3?

>Can molecular mechanics be used to investigate the potential conformational constraint imposed by the tetrahydropyran ring on the macrolide structure?

Fig.11 Part of reaction scheme (modified from )

Use of the GIAO approach to predict the ¹³C NMR spectra

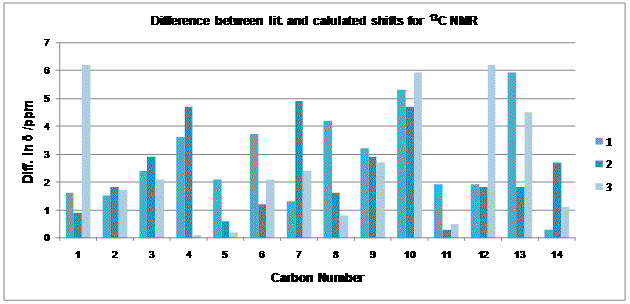
¹³C NMR for each isomer has been predicted and compared to the experimental results. Overall, each isomer shows reasonable agreement with the calculated values (Mean Δδ between Lit-Calc: A(1)=2.8ppm, B(2)=2.2ppm, 3=2.5ppm). There seems to be no consistency between the differences observed (Fig.13).The agreement observed is actually better than I expected. Based on the size of the macrolide and potential flexibility of the ring, it was not certain that the spectra predicted using this method, being highly sensitive to conformational flexibility, would actually give a reasonable result. It may have helped that each molecule was submitted for geometry optimisation (after initial MM2 optimisation) before the NMR prediction was made.

Table.11. ¹³C Comparison between literature values and those calculated for A(1)

Lit. δ/ppm	Calc.δ/ppm	C Assignment	δlit -δcalc /ppm
170.0 (C=O)	168.1	14	1.9
137.2	133.5	7	3.7
132.2	133.5	8	-1.3
74.1	75.7	1	-1.6
71.6	73.5	12	-1.9
71.3	69.2	5	2.1
66.9 (CH)	68.4	2	-1.5
40.6	46.5	15	-5.9
32.3	36.5	9	-4.2
31.2	36.5	11	-5.3
23.8	26.2	3	-2.4
22.1	25.7	4	-3.6
21.9 (CH2)	25.1	10	-3.2
18.7 (CH3)	19.0	18	-0.3

Although the agreement between literature values and those calculated are moderately reasonable (Fig.?), it is likely that not all the assignments match perfectly. Fully assigned ¹³C data could only be found for 2. When compared to the calculated assignments (Table.9.) , there are some discrepencies (albeit minor) between the two. This could be due to conformational differences, error within the calculations, or possibly, (although not having seen another complete assignment for comparison it is hard to say), error on the part of those who initially assigned the spectrum.

Fig.12 Labelled carbon assignment N.B all C assignments are based on this

Table.12. ¹³C Comparison between literature values and those calculated for B(2)

Lit. δ/ppm	Lit.C. Assignment	Calc.δ/ppm	C Assignment	δlit -δcalc /ppm
169.9	14	168.1	14	1.8
138.2	8	133.3	8	4.9
129.1	7	127.9	7	1.2
71.6	5	71.0	5	0.6
69.9	1	70.8	1	-0.9
69.7	12	70.0	2	-0.3
67.3	2	69.1	12	-1.8
39.9	15	38.1	15	1.8
32.1	11	36.8	11	-4.7
30.7	9	32.3	9	-1.6
27.8	3	30.7	10	-2.9
25.3	10	30.1	3	-4.8
22.6	4	27.3	4	-4.7
19.2	18	21.9	18	-2.7

Fig.13. Comaprison of Δδ for each molecule. N.B it has been assmed that the calculated assignments are more or less correct

The GIAO method does successfully differentiate 1 from both it's isomers 2 and 3. Whether the predicted spectra would have been good enough to allow for successful identification of the structures of naturally occuring aspergillides A and B is uncertain, and whether anyone actually tried to use similar computational methods is unknown. However, based on the findings here it seems reasonable to suggest that these methods would be useful, to some extent, in such a situation.

Table.13. ¹³C NMR Comparison between literature values and those calculated for 3

Lit. δ/ppm	Calc.δ/ppm	C Assignment	δlit -δcalc /ppm
173.5(C=O)	167.3	14	6.2
135.7	133.3	8	2.4
128.1	130.2	7	-2.1
81.6	82.0	1	-0.4
74.9	74.4	12	0.5
70.2	70.4	5	-0.2
69.9 (CH)	68.2	2	1.7
39.1	43.6	15	-4.5
34.5	40.4	11	-5.9
33.7	32.9	9	0.8
32.0	29.3	10	2.7
28.1	28.0	4	0.1
25.9 (CH2)	28.0	3	-2.1
20.9 (CH3)	22.0	18	-1.1

¹³C NMR for molecule 1,2, and 3

1	2	3
DOI:10042/to-4320	DOI:10042/to-4318	DOI:10042/to-4319

Conformational Analysis

As mentioned, there was some concern after aspergillide A had been selected to be studied that it may not have a rigid enough structure to give a good NMR result. As it turned out, the results were not too bad, suggesting the geometry optimisations were reasonably successful in finding a conformation quite close to the one adopted by the product. It is likely, therefore, that the tetrahyrdropyran entity does impose a notable amount of conformational restraint on the macrolides. N.B only after the optimised molecules had been submitted for NMR analysis was available X-Ray crystal structure data found, which would probably have reslted in a superior NMR prediction.

It was suggested that this conformational restraint may be particulary applicable to the (E)isomer(1 or 4b.), hence, it could not be ruled out that formation of 4b in the RCM step was both kinetically and thermodynamically unfavourable . Although it is difficult, without transition state analysis, to ascertain the kinetic properties of any of the molecules, the degree of flexibility of the isomers and the relative effects of changing the conformation slightly on the energy can be partly investigated using molecular mechanics. It should be noted that although attempts at modelling 4a and 4b were made, it was found that owing to the large degree of freedom of the benzyl group there existed many more possible conformations, and hence it proved easier to analyse 1 and 3.

Based on MM2 optimisations it was found that 3 is thermodynamically favourable in comparison to 1, hence supporting the literature findings . Changing the tetrahydropyran ring from twist boat to chair conformations has a more significant impact on the relative energy of 3 when compared to 1. In general small manipulations of the conformation of 1, followed by optimisation had little impact on the optimised geometry/energy of 1, in contrast to the effect on 3. Although, by no means conclusive, the findings seem to indicate that the tetrahydropyran ring adds a higher degree of structural rigidity to 1.

Table.15. Relative energies/kcalmol^-1 of the isomers 1,2 and 3 using MM2 optimisation

Molecule	Chair	Twist Boat
1	45.87	47.39
3	38.14	42.55
2	27.92	32.96