Third Year TS and Reactivity Lab: Tutorial
This is the tutorial for the third year TS and reactivity lab. For information about the lab and assessment return to the main lab page. The tutorial introduces the concepts behind the lab, and the calculations and techniques needed to complete the assessed exercises.
Introduction
Within this lab, you will be modelling several chemical reactions and analysing them by calculating Transition State (TS) structures. Locating transition states is an important step in confirming the mechanism of a reaction. For example, is a particular reaction stepwise or concerted? Will certain reaction pathways be favoured? In the lab, you will be analysing the geometry and the MOs of the TS structure and calculating reaction barriers to gain chemical insight into reaction mechanisms.
A simple potential energy profile (below, left) for a reaction shows the energy as a function of the reaction coordinate. The TS (2) is the point of maximum energy and links a set of reactants (1) and products (3) which are both energy minima. However, the potential energy profile is just a 1-dimensional simplification of the full Potential Energy Surface (PES) of the system. The total potential energy is a multi-dimensional function over all of the degrees of freedom in a system and not just the reaction coordinate. In the 1D potential energy profile, all other degrees of freedom have been optimised (the energy is minimised with respect to them) and then held fixed. The potential energy then only changes as the degree of freedom relating to the reaction coordinate changes. This means that the TS is only a maximum with respect to the reaction coordinate.

In reality, a chemical system can explore its full-dimensional PES (if it has enough energy) - it can be displaced away from its equilibrium position in any degree of freedom (independent of the representation). The full PES cannot be visualised but we can plot the potential energy against one or a combination of degrees of freedom (by keeping all others fixed). For example, plotting the 1D energy profile (left) or a 2D PES (right) which results from varying 2 different degrees of freedom.
On the 2D PES, the two energy minima can be connected by a reaction path (orange line) which will go through a TS. Plotting the energy as just a function along the reaction path results in the 1D potential energy profile on the left. The 1D energy profile is, therefore, just a slice of the full PES of the molecule and the TS is a maximum with respect to the reaction coordinate only.
Computational Methods
Computational methods allow us to study TS structure and reaction mechanisms that experimentally, we cannot investigate. Across a reaction, changes in the electron distribution result in the formation and breaking of bonds and changes in the type of bonding. Quantum Mechanical methods allow the electronic structure of a system to be calculated and analysed and for the energy of a system to be computed by solving the Schrodinger Equation. Therefore, we can use Quantum Mechanical methods to study reaction mechanisms and to locate TS stuctures.
During the lab, you will use two different Quantum Mechanical methods:
- PM6 - A semi-empirical method. This means that the method is parameterised using experimental data which saves computational time and resources but does result in lower accuracy than ab initio methods.
- B3LYP/6-31G(d) - B3LYP is a Density Functional Theory (DFT) method. B3LYP is reasonably fast compared to other DFT or ab initio methods and is capable of reproducing chemical data. 6-31G(d) is a basis set, which generally is a set of functions that typically mimic atomic orbitals and when combined linearly generate molecular orbitals. In a way, they are the building blocks of molecular orbitals. The higher the basis set, the more blocks are available to construct a molecular orbital, at the cost of computational effort.
Both of the methods approximate the Schrodinger Equation in different ways to calculate the energy of a system. For your introduction, you should be able to describe the main approximations of both of the methods. A useful resource for understanding the background of the lab and for writing your introduction is this introduction to Computational Quantum Chemistry.
Software Set up
To run the Quantum Mechanical calculations in the lab/experiment you will be using Gaussian and GaussView.
Gaussian is a computational chemistry program that will be used to run the calculations. GaussView is a visualiser/GUI that can be used to create input molecules for, run, and analyse Gaussian calculations. GaussView basically provides a front end to Gaussian and is the program that you will directly use.
You will be using a Azure Virtual Desktop to access the software needed:
https://www.imperial.ac.uk/admin-services/ict/self-service/connect-communicate/remote-access/azure-virtual-desktop/
Once connected, open softwarehub (https://softwarehub.imperial.ac.uk/) and install "Gaussian 16W - GaussView 6.1 - GMMX 3.0".
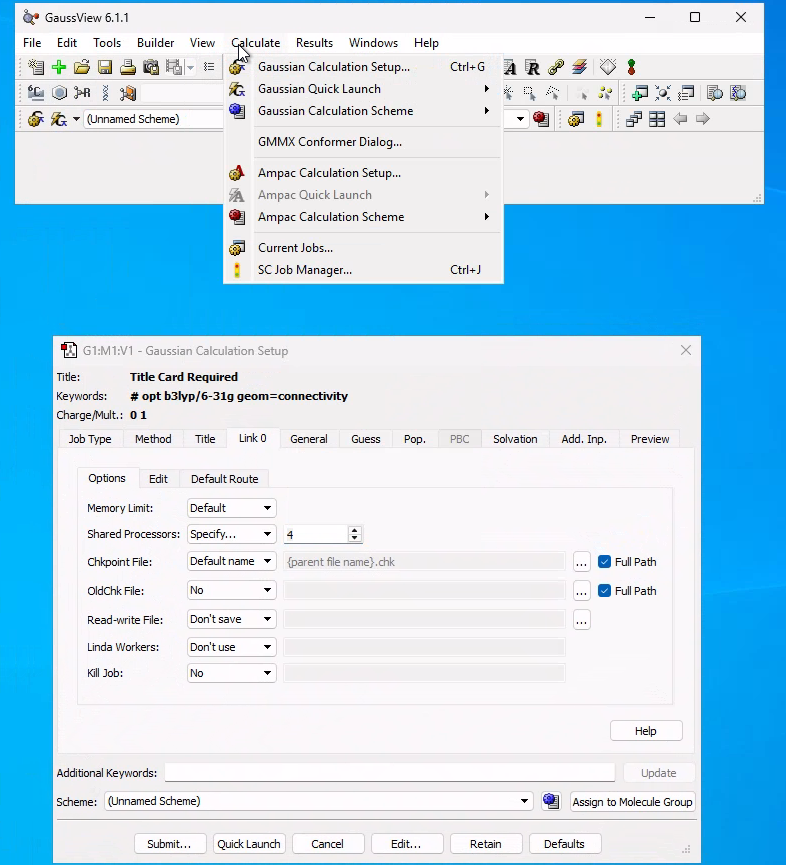
To run efficiently the simulations on this virtual desktop, we need to change the number of "Shared Processors" and set it to 4, as indicated in the figure:
When running your calculations, save your files in the folder "OneDrive - Imperial College London",
you can access it from "C:\Users\xyz123", where xyz123 is your username.
Create a sensible structure for your folders and files, in order to make easy the trouble shooting, for instance
C:\Users\xyz12\OneDrive - Imperial College London\TSR\exe1
C:\Users\xyz12\OneDrive - Imperial College London\TSR\exe2
C:\Users\xyz12\OneDrive - Imperial College London\TSR\exe3
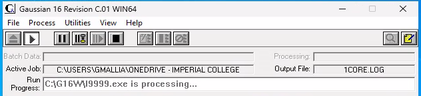
If your simulation get stuck at the link l9999.exe (see figure below), click on STOP, the icon with the square, and retrieve the files:
If you have any problems with accessing the Azure Virtual Desktop, let Dr Giuseppe Mallia know. You can use a PC in the computer rooms.
Tutorial: Cope Rearrangment
The classic example of a Cope rearrangement is the [3,3]-sigmatropic rearrangement of 1,5-hexadiene.
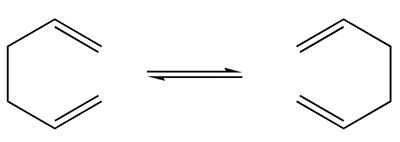
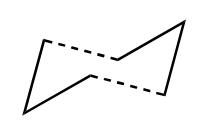
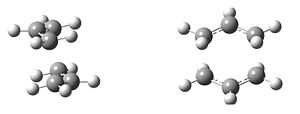
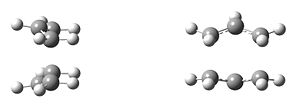
The mechanism of the rearrangement has been debated for a long time (stepwise/dissociative/concerted) but it is now accepted that it rearranges in a concerted, pericyclic fashion via a diradical transition state. The TS structure can either resemble the cyclohexane boat or chair conformation.
|
| |
|
| |
| Chair Transition State | Boat Transition State |
The two TS structures are likely to have different energies and therefore, the energy barriers for the rearrangements will be different. To calculate the full mechanism and the energy barriers we need to calculate the minimum and the TS structures.
Calculating a Minimum Energy Structure
Before trying to calculate the TS structures for the rearrangement, we will revise how to calculate a minimum energy structure. In previous undergraduate labs, you will have optimised simple molecules using electronic structure methods using the computational codes of Gaussian and PySCF. Optimising a molecule means that the energy is being minimised with respect to all degrees of freedom to locate a minimum on the PES. You will start by building and optimising a molecule of 1,5-hexadiene.
Build the Input Structure
In GaussView you will draw an initial structure of 1,5-hexadiene to optimise.
- Open a new molecule window in GaussView.
- In the builder window, select Element Fragments to view available fragments for all the elements. When you select a fragment it will appear in the builder window. The atom highlighted in blue indicates the atom that will be centered when you click in the molecule window to place the fragment.
- Select a Carbon Trivalent (S-S-D) fragment, these will be the terminal atoms of 1,5-hexadiene. Click in the molecule window to place the fragment from the builder window. Clicking once will place one carbon atom in the window.
- To join a second Carbon Trivalent (S-S-D) fragment to the first C atom click on the dangling double bond in the molecule window. Clicking on dangling bonds in the molecule window will place the fragment at the end of the bond. The molecule should now resemble ethene.
- Change the fragment to Carbon tetrahedral. To add the carbon to the growing chain, click on one of the 3 H atoms on the C atom just placed. Clicking on atoms in the molecule will replace the atom with the fragment.
- Add another tetrahedral carbon to a H atom of the C atom just placed.
- To create the second double bond, switch back to the Carbon Trivalent (S-S-D) fragment and add two final C atoms to the chain.
- To add one more carbon, click on one of the 3 H atoms on the C atom just placed. Clicking on atoms will replace the atom with the fragment.
You should now have a molecule of 1,5-hexadiene. The geometry of the molecule can now be optimised and analysed.
Optimisation and Frequency Calculation
To optimise the molecule and to confirm that the final structure is a minimum you will run an Optimisation and Frequency Calculation. Follow the calculation set up below to run a PM6 optimisation and frequency on your 1,5-hexadiene molecule.
In the Method tab select the method to use:
|
The calculation should start running and can take some time depending on the size of the molecule and the method being used. Only one calculation can be run at a time, so during the exercises, it is a good idea to work on your write-up while waiting for jobs to finish. If you think that the job has been running for too long or that something is not right then contact a demonstrator for help.
Once complete, open the log file to view the optimised molecule. If you get an error then try viewing the log file to see why it failed or contact a demonstrator for help.
Analysing a Calculation
The analysis section here applies to whether you are calculating a minimum energy structure or a TS. If the calculation has successfully run then the first check is to view the optimised geometry of the molecule and to check it looks as you would expect. If so, then you can analyse the structure further.
Convergence
Check that the calculation has properly converged to a stationary point on the PES. For each step in an optimisation (to a minimum or a TS), the gradient will be calculated to determine if the system is at a stationary point. If the gradient is small enough to be considered 0 then a stationary point has been found and the calculation will finish.
To check if your structure is fully converged:
- Open the log file either in an external application like Notepad++ or by selecting Results and then View File from the molecule window.
- Search for the phrase 'Converged?' to locate the convergence check section. The convergence check is printed after each step in an optimisation and you need to check the one for the final step which will be at the bottom of the file.
If your calculation has successfully converged the final convergence check section will look like this:
Item Value Threshold Converged?
Maximum Force 0.000098 0.000450 YES
RMS Force 0.000010 0.000300 YES
Maximum Displacement 0.001379 0.001800 YES
RMS Displacement 0.000379 0.001200 YES
Predicted change in Energy=-4.942954D-08
Optimization completed.
-- Stationary point found.
This job has landed on a stationary point. Compare to the following, which has not converged properly:
Item Value Threshold Converged? Maximum Force 0.000155 0.000450 YES RMS Force 0.000021 0.000300 YES Maximum Displacement 0.002340 0.001800 NO RMS Displacement 0.000561 0.001200 YES Predicted change in Energy=-2.681147D-07
If your calculation is not converged, copy and paste the molecule from the .log calculation into a new molecule window. Rerun an Opt+Freq (to either a minimum or TS, depending on what you are trying to calculate) calculation and check the convergence again. If you experience the same problem again then ask a demonstrator for help.
Frequencies
You should now have a structure that has converged to a stationary point. But what type of stationary point has it converged to? The results of a frequency calculation can be used to check through the number of imaginary frequencies that the molecule has.
- In the open log file search for the phrase 'Frequencies'. This will take you to the start of the section where all of the vibrational modes of the molecule are outputted.
- Check the number of imaginary frequencies, these will appear as negative numbers in Gaussian and will be the first listed vibrational modes as they are organised in increasing order.
- For 1,5-hexadiene and any other minimum energy structure there should be no imaginary frequencies.
- If you have calculated a TS structure there should be a single imaginary frequency. If this is the case, view the mode in GaussView - does the motion of the imaginary frequency look like you would expect it to? I.e. does it look like it would change the TS to resemble the reactants/products of the reaction?
- If there is more than one negative frequency then you have a higher order saddle point. This is likely to be because the starting structure input to the calculation was not close enough to the real TS or minimum structure on the PES. Reopen your input file and try to amend the structure to make it closer to what the TS will resemble.
Energies and Reaction Barriers
You should now have an optimised minimum energy structure of 1,5-hexadiene which is fully converged and has no imaginary (negative) frequencies. The structure corresponds to a minimum on the PES of 1,5-hexadiene. However, there are several conformers of 1,5-hexadiene and the conformer you have optimised could be the global minimum or just a local minimum. To compare different structures on the PES and to calculate reaction barriers we need to know the energy of the molecule.
The electronic energy is calculated (in h) at every step during an optimisation and can be found in the log file by searching for 'SCF Done' in the file.
SCF Done: E(RPM6) = 0.295575641466E-01 A.U. after 2 cycles
The final one in the final is the optimised electronic energy and can also be viewed in the molecule summary in GaussView (Under Results and then Summary).
However, to calculate reaction energies and reaction barriers, thermal contributions to the energy and the ZPE need to be considered. These corrections are calculated during a frequency calculation and the energy, enthalpy and free energy values for a molecule are computed. To find the quantities required:
- In the open log file search for the phrase 'Thermochemistry'.
The thermochemistry section that follows contains information about the molecule and calculates several important quantities. More about the section can be found out here: [[1]], where section 3 goes through the thermochemistry output of a frequency calculation.
- The first line of the section will show the 'temperature' of the calculation. Different temperatures can be specified when running the job to explore energies and barriers at different temperatures. The default temperature is 298.15 K (room temperature).
- Scroll down to the section which computes the corrections and the thermodynamic quantities. For a conformer of hexadiene at the PM6 level the output is:
Zero-point correction= 0.131084 (Hartree/Particle) Thermal correction to Energy= 0.138805 Thermal correction to Enthalpy= 0.139749 Thermal correction to Gibbs Free Energy= 0.097643 Sum of electronic and zero-point Energies= 0.160642 Sum of electronic and thermal Energies= 0.168362 Sum of electronic and thermal Enthalpies= 0.169306 Sum of electronic and thermal Free Energies= 0.127201
- The Sum of electronic and thermal Enthalpies gives the thermally corrected Enthalpy for the molecule. This is the quantity used to calculate activation enthalpies (ΔH = HTS - Hreactants) and are usually the quantity needed to compare to some experimental values, depending on what measurement has been experimentally carried out in the lab.
- The Sum of electronic and thermal Free Energies gives the thermally corrected Gibbs Free energy for the molecule. This is the quantity used to calculate reaction energies (ΔG = Gproducts - Greactants) and reaction barriers (ΔG = GTS - Greactants) at room temperature.
- If there are multiple reactants/products then make sure that you use the optimised isolated structures (the assumption that they react from infinite separation) to calculate the correct energy barrier from.
For your 1,5-hexadiene molecule locate the Thermochemistry section and compare the output to the above, is it the same conformer? Note that there is an error in the values calculated and they can only really be compared up to 4dp in h (~1 kJmol-1).
- Is the conformer you have calculated a global or local minimum? Compare your conformer and the free energy to the range of 1,5-hexadiene conformers here.
Calculating a TS Structure
To calculate the energy barrier for the Cope rearrangement you need to know the energy of the TS. Calculating a TS is more difficult than calculating a minimum energy structure. The TS is a maximum in one degree of freedom (the reaction coordinate) meaning that a conventional optimisation (where all degrees of freedom are minimised) doesn’t work. Instead, a different method - a TS Optimisation - is used in Gaussian. This method requires that the starting structure has at least one imaginary (negative in Gaussian) frequency which the TS optimisation can follow.
When starting a TS Optimisation, it is important to begin from a guess structure which is close to the first-order saddle point structure that you wish to locate. The further the starting guess TS structure from the true point on the PES, then the more likely it is that the calculation will follow the wrong imaginary frequency and result in an incorrect TS structure. For example, in the image below, the guess TS 1 structure is too far away from the actual saddle point. The calculation would struggle to find the correct TS structure and will most likely fail. In most cases, the wrong TS will be found (check the negative vibrational mode - does it look like the motion you would expect to see?) or there will be multiple imaginary frequencies. A converged structure with multiple imaginary frequencies is indicative of a higher-order saddle point.

In comparison, guess TS 2 is much closer to the structure it is aiming to find and will be more likely to locate the TS successfully. Therefore, chemical intuition plays a large part in trying to calculate TS structures, you need to consider how molecules change between the reactants and products and how the TS may look.
As seen before, there are two possible TS structures for the Cope rearrangement: the chair, and boat TS. You will start by trying to build the boat TS.
Build the Input Structure
As with the 1,5-hexadiene optimisation, an initial structure for the TS has to be built in GaussView. As mentioned above, the closer this initial structure is to the real TS structure on the PES, the more likely the calculation will be to calculate the correct TS.
- Open a new molecule window in GaussView.
- Select a Carbon Trivalent (S-A-A) fragment for the central atom and place one in the molecule window.
- For the neighbouring carbons choose Carbon Trivalent (S-S-D)'
You should now have a fragment that resembles half of a TS. In addition, at the bottom of the molecular editor window, it should read 8 atoms, 23 electrons, neutral, doublet. This indicates that the fragment is a radical.
- Copy the whole fragment (it should appear in the builder window as the copied fragment). Paste a second allyl radical fragment below the first by clicking in the same molecule window.
Currently, your molecule won’t resemble the boat TS structures. If you were to run a calculation on this structure it would not be able to calculate the correct TS on the PES.
To improve the structure, position the two fragments to resemble the boat transition state above.
- You can use the GaussView keyboard commands to help:
- alt + right mouse button: rotates a single fragment
- alt + shift + right mouse button: translates a single fragment.
- (Check the GaussView Tutorial for more help.)
- The Modify Bond, Angle, and Dihedral tools in the GaussView toolbar may also be helpful.
- You can use the GaussView keyboard commands to help:
The structure in your molecule window should now resemble the boat TS. However, it is likely to correspond to a geometry that is very far from the true TS on the PES. This means that the calculation will struggle to calculate the boat TS successfully.
To improve the structure we need to consider the chemistry and how the structure changes across the rearrangement.
- Think about what bond distances, angles, or dihedrals change during the Cope rearrangement. A bond will break and another bond will form between the two pairs of terminal carbons in your fragments.
- Using the Modify Bond tool, position the two pairs of C atoms where the bonds form/break to a distance ~2.2. Å. This distance is larger than that of a C-C bond but small enough that the two fragments will be close enough to interact.
- Changing the distances may affect the positions of the fragments so make sure to keep repositioning the fragments and checking that the C-C distances stay close to 2.2 Å until you are happy that you have a good structure that closely resembles the boat TS.
You are now ready to input your guess TS structure to a TS optimisation and frequency calculation.
TS Optimisation and Frequency Calculation
To optimise the molecule to a TS you will again run an Optimisation and Frequency Calculation, but this time you will be optimising to a TS. Follow the below procedure to set up and run a TS Optimisation and Frequency calculation at the PM6 level on your boat TS structure.
|
The calculation should start running. If the calculation terminates with an error then check the log file to see the error and if possible, view the last structure calculated by opening the log file in GaussView. (Note that you will get a warning about an error termination but if you click ok it should show the last calculated structure before the termination). If the structure looks very different to the TS that you were expecting, then the input structure was too far away on the PES. Reopen the input file and try rearranging the fragments to more closely resemble the TS.
Analysis
Once you have calculated the boat TS you need to check and analyse the structure.
- Do you have a converged, TS structure? - As with 1,5-hexadiene, check the convergence and the frequencies of the structure.
- Do you have the correct TS structure? - There should be a single negative frequency for the molecule at ~900 cm-1. If you view the mode in GaussView you should see the two pairs of terminal carbons asynchronously moving together. Does this look like the movement you would expect in the Cope rearrangement?
A second confirmation tool to use to check that you have the correct TS is to run an Intrinsic Reaction Coordinate (IRC) calculation.
IRC Calculation
An IRC calculation can be used to confirm that your TS is located on the correct reaction pathway that you are investigating. An IRC calculation uses the single imaginary frequency of the TS to follow a minimum energy pathway from the TS to the minima that it connects on the PES. The end minima structures of the IRC calculation can then be compared to the products/reactants that you expect to form. If the structures resemble each other then you have calculated the correct TS as it lies on the correct reaction path, linking the reactants to the products.
Run an IRC on your boat TS to find the two minima it corrects. Note that the TS is symmetric and that the minima will be identical so the IRC calculation only needs to be run in one direction.
We are only running IRC calculations using PM6 because the calculations are expensive and so take a very long time to run when also using an expensive method and basis set (e.g. B3LYP/6-31G(d)). If you only have a TS structure optimised at the B3LYP/6-31G(d) level then running a TS optimisation on this structure using PM6 and then an IRC will actually be faster.
|
IRCs can be problematic, especially for reactions where the PES is not well defined. Some common problems with IRCs are shown below and if you are having trouble getting them to run successfully ask a demonstrator.
Once the IRC calculation has run successfully - whether this is until a stationary point has been found in both the reverse and forward direction (if applicable) or if it has reached the maximum number of a high number of steps (e.g. 100) then you can analyse the endpoints.
|
- Does the boat TS connect to your original 1,5-hexadiene optimised structure? Compare the optimised minimum from the IRC with your original 1,5-hexadiene optimised structure.
- Which 1,5-hexadiene conformer does the boat TS connect to? Compare the optimised minimum from the IRC to the other conformers of 1,5-hexadiene.
- What is the reaction barrier? Calculate the free energy reaction barrier (at room temperature) for the Cope rearrangement between your optimised boat TS and the optimised minimum energy 1,5-hexadiene that it connects to.
Calculating the Chair TS
Now that you have the boat TS, try applying the above process of calculating a TS to locate the chair TS at the PM6 level:
- Build a guess input chair TS structure.
- Run a TS Optimisation and Frequency calculation.
- Confirm that you have calculated the correct TS and that it has converged to a stationary point.
- Run an IRC calculation (in one direction only) and optimise the endpoint to a minimum.
You can now compare the two pathways:
- Does the chair TS connect the same 1,5-hexadiene conformer as the boat TS? Compare the two optimised minima from the boat and chair TS IRC calculations.
- Does the chair or the boat TS have a lower barrier? Calculate the free energy reaction barrier (at room temperature) for the Cope rearrangement going through the chair TS and compare it to the boat TS.
Improving the Level of Theory
You have just calculated the stationary points (minima and TS) for the Cope rearrangement at the PM6 level of theory.
PM6 is not an accurate method for some systems (you may want to consider what systems it may be accurate for in your report write up). To get more accurate energy barriers, higher levels of theory need to be used for the calculations. The main issue with more accurate computational methods, however, is that they are usually more computationally expensive, this means that the calculations take longer to run.
In the lab, you have limited computational resources and so are limited to the accuracy of the method that you can use. To help this, a cheaper method (e.g. PM6) can be used to calculate initial structures that may be hard to find (i.e. TS structures). The optimised PM6 molecule can then be used as an input geometry for a calculation at a higher level of theory (e.g. B3LYP/6-31G(d)). This means that the starting geometry for the higher level calculation is much closer to the true structure it is trying to calculate on the PES than an initial input guess drawn in GaussView. The closer the starting structure is to the true result on the PES, then the faster the calculation will be.
It is important to note that different methods do give slightly different PESs. The PES gives the energy as a function of the geometry of a system. Different methods calculate the energy in different ways (they make different approximations). Therefore, the PM6 PES will be slightly different from the B3LYP/6-31G(d) PES for a molecule. The PES for the higher level of theory should be more accurate (hence, giving more accurate energy barriers). However, the two PESs should not be too different and so an input PM6 TS structure to a B3LYP/6-31G(d) calculation may change to optimise to a TS but the optimisation should only take a couple of steps.
Compare the energy barriers and any geometry changes for the two Cope rearrangement pathways (via the chair and boat TS) between the two computational methods: PM6 and B3LYP/6-31G(d):
- Optimise the stationary points from your two Cope rearrangement pathways (minima, and the chair and boat TS) and run frequency calculations at the B3LYP/6-31G(d) (you need to change the method in the Method tab of the job set up).
- Check the convergence and frequencies of the structures.
- Calculate the B3LYP/6-31G(d) energy barriers for the chair and boat TS.
- Is the same TS lower in energy for both methods?
- What is the difference between the two (boat and chair) reaction barriers (free energy) for both methods?
Remember, you can only compare energy differences (e.g. reaction barriers) across two different methods and not raw energies.
The Gibbs Free Energies (G), reaction barriers (ΔG), enthalpies (H) and actiavtion enthalpies (ΔH) for both the chair and boat TS are below: Compare your values:
| Structure | H (kJmol-1 PM6) |
ΔH (kJmol-1 PM6) |
G (kJmol-1 PM6) |
ΔG (kJmol-1 PM6) |
H (kJmol-1 B3LYP/6-31G(d)) |
ΔH (kJmol-1 B3LYP/6-31G(d)) |
G (kJmol-1 B3LYP/6-31G(d)) |
ΔG (kJmol-1 B3LYP/6-31G(d)) |
|---|---|---|---|---|---|---|---|---|
| 1, 5-Hexadiene (Boat Minimum) | 445 | 335 | -615576 | -615680 | ||||
| TS Boat TS) | 634 | 189 | 539 | 205 | -615404 | 172 | -615500 | 180 |
| Minimum (Chair) | 443 | 340 | -615575 | -615677 | ||||
| TS Chair | 598 | 156 | 506 | 166 | -615438 | 136 | -615532 | 146 |
One experimental free energy for the chair TS is 35 kcalmol-1 [[2]], which method gives a more accurate reaction barrier? Why might some experimental values not be comparable to the computationally calculated values?
Tutorial: Xylylene-SO2 Diels Alder Cycloaddition
In the previous example, you constructed a guess TS structure directly from fragments because you knew what the real TS should look like. As reaction systems become more complex, you will not know enough about the form of the TS to draw a guess structure straight away. In this case, the reactants or products can be used as starting structures and bond lengths can be altered to resemble the TS. Some points to consider when constructing a TS this way are:
- Generally, start with whichever of the reactants or the products have fewer molecules, so for a dimerisation reaction choose the dimer.
- Try to recognise what bond lengths, angles, or dihedrals will change during the reaction. Modify the values using the appropriate editing tools.
- In some cases it may not be enough to only change the atoms directly involved in the reaction. If this hasn't worked then try altering neighbouring atoms to reflect the change in hybridisation they might undergo.
- E.g. In a classic Diels Alder reaction, 3 double bonds become single bonds and one single bond becomes a double bond, so it might be worth changing these values to somewhere in between. The dienophile carbon atoms become sp3 hybridised, so the neighbouring atoms might need to be distorted a little to reflect this.
- This can be a difficult approach if the reaction barrier is very early or late and the minima that you start from is far away in geometry from the TS. E.g. There can be problems if you start from the products but your TS resembles the reactants, in which case you may want to retry from the other minima.
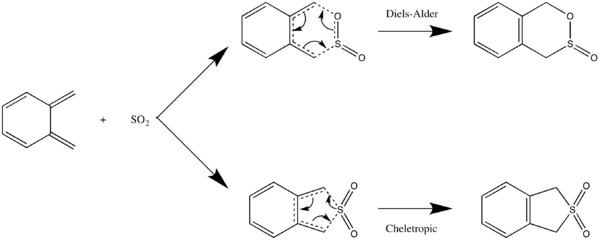
You will now use an example of a hetero-Diels Alder reaction to try to calculate a more complex TS structure. In the reaction, SO2 is used as a dienophile and reacts with Xylylene.
Build the Input Structure
There are three possible TS structures for the reaction of SO2 and xylene: the chelotropic TS for the chelotropic reaction path, and the endo and exo TSs for the Diels-Alder reaction. We will try to construct the exo Diels Alder TS here.
Without knowing the direction of approach of SO2 or whether the barrier is early or late, it can be difficult to just draw a guess TS directly. Therefore, we'll start from the product as this is a single molecule and potentially easier to work from.
- Open a new molecule window to construct the product in.
- In the builder window, select Ring Fragments and choose naphthalene. Two carbons at the end will be replaced to form the SO2 group.
- Replace the two atoms with appropriate O and S fragments.
- Select the 'Add Valence tool from the GaussView toolbar and add the additional hydrogens to form xylylene.
- Run and optimisation and frequency calculation on the product to calculate a minimum energy structure. In the resulting molecule, you will probably have some negative frequencies. This is due to the symmetry constraints of the initial fragments used. In the Vibrations window, use manual displacement to break symmetry and reoptimise. In the future, if you expect issues with symmetry you can try to break it before the initial optimisation to save time by modifying the geometry of the molecule before the calculation.
Now that you have an optimised product, the structure can be edited to try to construct the potential TS. The reactants are xylylene and SO2 so the bonds connecting these are the two geometric parameters likely to change the most between the reactants and products.
- Delete the bonds between xylylene and SO2 and separate them by about 2.0 Å for the C-O pair and 2.4 Å for the C-S pair.
The rest of the molecule is quite complex. Another trick to get closer to the true TS structure is to freeze the coordinates that are involved in the reaction and to minimise all of the other coordinates that do not change between the reactants and products. Freezing the distances between xylylene and SO2 will mean that they are ignored by the calculation and the rest of the molecule can be optimised to a minimum. This moves the guess TS structure closer to the true TS on the reaction PES.
- Select Tools from the main GaussView menu and then Redundant Coordinate Editor.
- In the Redundant Coordinate Editor click Add to add a new parameter.
- Select the S and C atoms of the C-S distance that we want to freeze in the molecule window.
- Back in the Redundant Coordinate Editor, change 'Unidentified' to 'Bond' and 'Add' to 'Freeze'.
- Repeat the process with the O and C atom pair.
- Run an Optimisation and Frequency Calculation on the structure, optimising to a minimum. You should notice that the keywords line now contains opt=modredundant, this refers to the frozen coordinates.
The calculation should successfully run. If it terminates with an error then check the log file. Search for the phrase `Optimized` and if it finds a list of 'Non-Optimized Parameters' then this means that the calculation ran out of steps before it could reach convergence. Try running the optimisation and frequency from the final structure of the calculation, making sure the coordinates are still frozen.
Once you have a structure that is close to a minimum in all degrees of freedom but the frozen distances, you can unfreeze the coordinates and try to run a TS Optimisation.
- Copy the resulting xylylene-SO2 structure, from the optimisation above, from the log file to a new molecule window. This should remove the frozen coordinates but you can check that they have been removed by opening the Redundant Coordinate Editor and making sure that no parameters are listed.
- Run a TS Optimisation and Frequency calculation on the structure.
A TS should be calculated successfully. Check the convergence and the frequencies, does the vibrational mode for the imaginary frequency look like you would expect?
Conclusion
You have learned how to calculate and analyse minimum energy and TS structures on a reaction PES. Calculating TS structures requires chemical intuition and to help locate the correct TS there are several tricks/techniques that you should now be able to use:
- Use GaussView to construct a good guess TS structure directly from chemical knowledge.
- Modify a reactant/product structure to resemble how the TS may look.
- Work out the geometric parameters (bonds lengths, angles and dihedrals) that may change a lot during the reaction.
- Modify the values of the parameters to values between the products and reactants. E.g. Where bonds form or break, the participating atoms can be placed at distances midway between a bond and not-bonded.
- The parameters can be frozen and the rest of the molecule can be optimised to a minimum first, to optimise any parameters that do not change across the reaction.
You have also calculated energy barriers and run calculations at different levels of theory.
Move on to the assessed exercises and apply the techniques used in the tutorial to the reactions.