Third Year Computational Chemistry Lab

3rd Year Computational Chemistry Lab

Ammonia

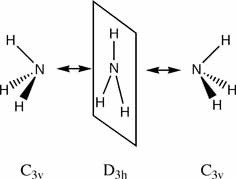
Although the ammonia molecule (NH3) is a small and very simple molecule, it is also very interesting. In the first part of this lab you are going to do some calculations on NH3.

Ammonia is a colorless gas under standard conditions, with a sharp, acrid odor. Under 1 atm, it boils at -33.4°C and because it can be liquefied at room temperature it often used as a coolant. Ammonia is also highly soluble in water, and under standard conditions, a saturated solution is about 30% ammonia. The solution is a powerful cleaning agent, and a little added to your window-cleaning solution not only cleans but also helps prevents streaking. Nitrogen is an essential element for plant growth, but plants cannot use elemental nitrogen directly from the atmosphere, N2. Nitrogen is often added to fertilizers as ammonia ("anhydrous ammonia"), or as ammonium compounds, soil bacteria then convert it to nitrite, NO2-, which is then oxidized to nitrate and absorbed by the plants. Many salts are formed with the ammonium ion NH4+. Smelling salts is ammonium carbonate, (NH4)2CO3, which decomposes readily into ammonia (which provides the strong smell), water and carbon dioxide.

The low potential barrier between the two structures of ammonia, means that the H atoms can tunnel from one side of the nitrogen atom to the other, this is called "inversion". This purely quantum phenomenon causes "inversion doubling" of the vibrational modes of ammonia. The ammonia MASER uses these levels to achieve (coherent) laser like light in the microwave region. Another use of these purely quantum mechanical levels is in quantum computing. The ammonium molecule can also be used as a "qubit" (a quantum information unit). If we say the state on the left of the diagram above is the "left" state, and the state on the right of the diagram above is the "right" state. Then the ammonia molecule flips between these two states many times a second. However a linear combination of these two states forms a "stationary state" (a state that does not change over time, and hence the word stationary!). The two physical states form "+" and "-" stationary states (which are eigenvectors of the system Hamiltonian). A quantum computer will force a change from one state to the other (by applying "light" of the right resonant frequency). This is equivalent to the 0 and 1 of ordinary electron based computing.

Activities

You are going to examine the inversion barrier for this system. It is a kind of "reaction path" and so you we will be optimising ground states, transition states, and using scanning techniques commonly applied when studying reaction mechanisms. (A1) optimise the ground state for NH3. Start with a 3-21G basis set and the HF method (be sure to save your checkpoint file in each case as you will need it in the next step, if you don't know how to use checkpoint files ask the demonstrator.)

• generate an NH3 molecule in gaussview and optimise it (save your output file)
• determine the symmetry of your molecule by reading the output .log file
• what is the symmetry of your molecule? It should be C3v
• add the extra keyword "nosym" and rerun the optimisation
• manually edit the gaussview input file and change a couple of parameters to reduce the symmetry (for example make B1=1.01, and A1=109.5 )
• what is the symmetry of your molecule? It should be C1
• use the file provided and run the optimisation (nh3_highsym.txt)
• what is the symmetry of your molecule? It should be D3h

Look over the three optimisation jobs and consider the following questions:

• has the symmetry made any difference to the optimisation process?
• hint(1) -> look at the output file where is says

"Optimization completed. 
-- Stationary point found." 

• hint(2) -> look at the output file where it says

"Job cpu time:"

• do you reach the same structure in all cases?
• what is the energy of each structure?
• can a molecule "break symmetry" during an optimisation?
• what implications does this have if you enter a high symmetry structure to optimise?
• what implication does symmetry have for the time it takes to do a calculation?

Optimise the ground state and the inversion transition state for NH3 at a higher level. Start a new set of calculations using the results from your "low level" calculations, you should know what the extra keywords "geom=checkpoint" and "guess=read" mean and use them (if you don't ask a demonstrator). Use a 6-31G(d,p) basis set and the B3LYP method. NH3 is a small molecule and the calculations do not take a lot of time, however when you start doing much larger calculations these "preparation" or lower level jobs are very important for saving time and processing (which costs money!)

• optimise the ground state for NH3 under C3v symmetry
• optimise the inversion transition state for NH3 under D3h symmetry. The D3h structure is the transition state in this reaction.
• how long do these calculations take compared to your low level ones?
• has the relative energy E(D3h)-E(C3v) changed much between the HF/3-21G and B3LYP/6-31G(d,p) sets of calculations? This energy is the barrier height to inversion.

Individual Projects

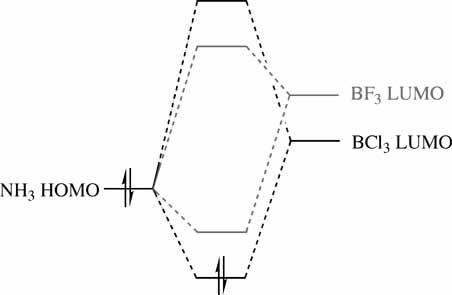
Boron based acids

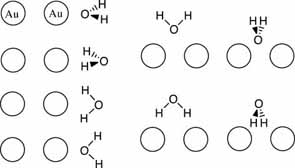
Gold interactions with water