The theoretical Background

The Born-Oppenheimer approximation

Since nuclei are much heavier than electrons, their velocities are much smaller. To a good approximation, the Schrödinger equation can be separated into two parts :
– One part describes the electronic wave function for a fixed nuclear geometry.
– The second describes the nuclear wave function, where the electronic energy plays the role of a potential energy.

In other words, the kinetic energy of the nuclei can be treated separately. This is the Born Oppenheimer approximation. As a result, the electronic wavefunction depends only on the positions of the nuclei.

The Potential Energy Surface (PES)

Physically, this implies that the nuclei move on a potential energy surface (PES), which are solutions to the electronic Schrödinger equation. Under the BO approximation, the PES is independent of the nuclear masses, and it is the same for isotopic molecules.

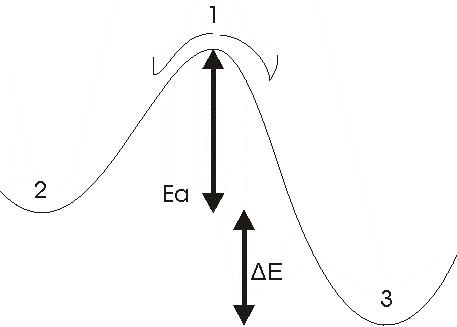
Reaction along the PES

Generally a reaction occurs along a potential energy surface, and this graph corresponds to a reactive way in 2D.

If a molecule is around 1 it is unstable and so it is going to change to 2 or to 3 it depends, but what is sure it is that it will move to get set. Indeed, around 2 or 3 the molecule is stable it is in a potential pit.

Ea corresponds to the energy of activation that needs the molecule to pass over the barrier and thus go from 2 to 3. So because of this instability the form in 1 can not be observed but in theory we can obtain this form and we can optimize the geometry around this position.
Indeed, we just need to specify to Gaussian that we want an optimization in a Transition State (TS Berny), and then Gaussian will optimize the geometry at this position.

The $Δ E$ corresponds to the difference of energy between the two stable forms (2 and 3). And each of these energy correspond to the energy at the minimum of geometry (ask Gaussian to make the optimization at the minimum, in this case you just specify that you want an optimization of geometry in a potential pit).

3N-6 coordinates of the PES

Because the electronic energy is a function of all the degrees of freedom in the system, each point of the PES is an approximation of the Schrodinger equation at a specific geometry. So, in a PES graph we may visualize each electronic state of a N-atom molecule as a (3N-6) dimensional surface.

Back to Resgrp:comp-photo-c3h6-tutorial