Rep:Mod:zc1111

Third Year Computational Lab- Part 1

EX₃ Section

Geometry Information

geometry data
	BH3	BBr3	GaBr3
r(E-X)	1.19	1.93	2.28
θ(X-E-X)	120.0	120.0	120.0

When comparing structures, it is important to define the terms we use to describe the simiarities and differences. I shall starts with explaining what a bond is. A bond can be thought of to be a distribition of electron density and is the sum of all orbital contributions where the molecular orbitals are delocalised^[2]>, There are three main types of bonding, ionic, covalent and metallic, howeever we can also have covalent bonds with ionic character and vice versa. There are also weaker types of bonds such as hydrogen bonding, dispersion forces to name a few. Traditional theory depicts bonds as 2c-2e shown through a solid line between the atoms. This doesn't tell us much about the hybridisation of the orbitals and their relative contributions. While valence bond theory is useful for small molecules, MO theory tells us more about the electron distribution and the orbital shapes and contributions. Gaussview sometimes doesnt draw in the bonds where we would expect them, however this doesnt mean the bond is not there, it simply means that the bond length is outside the calibrated range and so Gaussview considers the two atoms not to be bonded.

For comparison of bond strengths, the terms weak, medium and strong ca be used for relative comparison. The bond strength can be quantified by looking at the bond dissociation energy and comparing to similar molecules either by type of bond, or with only the central atom or ligand changed. For example, C-H, C-Br, C-F, where the C-F bond can be considered strong at 490 kj/mol, the C-H bond medium at 410 kj/mol and C-Br weak at 285 kj/mol. ^[5].

Comparing BX₃ we can see the B-H has a shorter bond distance than B-Br. This is due to the fact that Br is in period 3 and has a much larger atomic radius, resulting in relatively poor orbital overlap compared to B-H. This results in the formation of the longer, weaker B-Br bonds. Bond angle is not affected and remains 120.0 throughout.

Comparing MX₃ we can see that Ga-Br is a longer weaker bond than B-Br. Again this is due to poor orbital overlap as Ga is much larger than B and forms longer, weaker bonds with Br. Changing the ligand increases the bond length, the larger the ligand the longer the bond length as B-Br bond length is larger than B-H. This can be rationalised using the fact that Br has more electrons that H and so the atoms must be further spsrt to reduce the repulsion between the bonding electrons and the electrons on Br. H and Br are very different as H is smaller with a smaller van der waals radius and is also less electronegative than Br at 2.04 compared to Br's 2.96 on the Pauling scale.

Changing the central atom changes the bond length as the larger the central atom, the larger the bond length due to the increased van der waals radius of the larger central atom. This is shown when changing B to Ga. Both are in Group 3 of the periodic table, howeever Ga is further down rhe group and is larger than B due to the increase in the number of elecrons. It therefore has a larger van der waals radii. B is more electronegative than Ga at 2.96 compared to 1.81 (Pauling scale).

BH₃:B3LYP/3-21G

Optimization log file

The optimisation log file can be found here

Geometry

Summary Data

Convergence Table

Jmol

C_s

 Item                        Value     Threshold  Converged?
 Maximum Force               0.000220     0.000450     YES
 RMS     Force               0.000106     0.000300     YES
 Maximum Displacement        0.000940     0.001800     YES
 RMS     Displacement        0.000447     0.001200     YES

BH3 321-G optimisation

As you can see a better optimisation is needed as the point group is C_s and the optimised molecule must have the correct point group. A better basis set is needed.

BH₃:B3LYP/6-31G (d,p)

The optimisation log file can be found here

Geometry

Summary Data

Convergence Table

Jmol

C_s

Item               Value     Threshold  Converged?
 Maximum Force            0.000012     0.000450     YES
 RMS     Force            0.000008     0.000300     YES
 Maximum Displacement     0.000055     0.001800     YES
 RMS     Displacement     0.000039     0.001200     YES

BH3 631-G optimisation

GaBr₃:B3LYP/LANL2DZ

Optimization log file

The optimisation log file can be found here DOI:10042/193878 GaBr3 opt link

Geometry

Summary Data

Convergence Table

Jmol

D_3h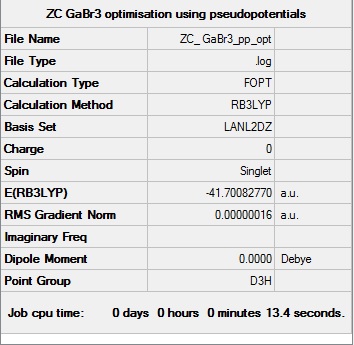

  Item                     Value     Threshold  Converged?
  Maximum Force            0.000000     0.000450     YES
  RMS     Force            0.000000     0.000300     YES
  Maximum Displacement     0.000003     0.001800     YES
  RMS     Displacement     0.000002     0.001200     YES
  Predicted change in Energy=-1.307633D-12
  Optimization completed.
    -- Stationary point found.

GaBr3 LANL2DZ optimisation

BBr₃:B3LYP/6-31G(d,p)LANL2DZ

Optimization log file

The optimisation log file can be found here DOI:10042/193966

Geometry

Summary Data

Convergence Table

Jmol

C_s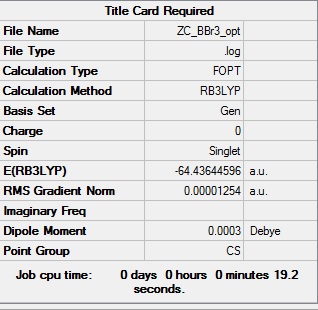

  Item               Value     Threshold  Converged?
 Maximum Force            0.000028     0.000450     YES
 RMS     Force            0.000011     0.000300     YES
 Maximum Displacement     0.000141     0.001800     YES
 RMS     Displacement     0.000075     0.001200     YES
 Predicted change in Energy=-3.051534D-09
 Optimization completed.
    -- Stationary point found.

BBr3 optimisation

Further Optimisation

The optimisation log file can be found here D-SPace DOI:10042/193965

Geometry

Summary Data

Convergence Table

Jmol

D_3h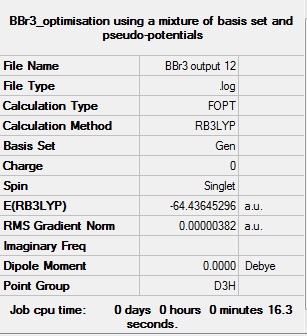

  Item               Value     Threshold  Converged?
 Maximum Force            0.000008     0.000450     YES
 RMS     Force            0.000005     0.000300     YES
 Maximum Displacement     0.000036     0.001800     YES
 RMS     Displacement     0.000023     0.001200     YES
 Predicted change in Energy=-4.027615D-10
 Optimization completed.
    -- Stationary point found.

BBr3 optimisation

BH₃ Frequency Analysis:B3LYP/6-31G(d,p)

Frequency file: here


summary data	low modes
	Low frequencies --- -14.5183 -14.5142 -10.8197 0.0010 0.0169 0.3454 Low frequencies --- 1162.9508 1213.1230 1213.1232

Vibrational spectrum for BH₃


wavenumber	Intensity	IR active?	type
1162	93	yes	bend
1213	14	very slight	bend
1213	14	very slight	bend
2583	0	no	stretch
2716	126	yes	stretch
2716	126	yes	stretch

|

In the spectrum,only 3 vibrational peaks are observed even though there are 6 vibrations in total. The vibration at the frequency of 2583 cm-1 was not observed as it is not IR active.It is a stretch along 3 B-H bonds where the dipole moments cancels each other out and giving rise to zero intensity. For it to be seen there needs to be a change in dipole moment of the molecule and as the molecule is trigonal planar, D3h, the stretches that do not break the symmetry are not observed in the spectrum. The vibration at 1162cm-1 is an umbrella bend, the two vibrations at 1213 cm-1 that are due to bending are degenerate and give rise to a single peak and the two vibrations at 2716 cm-1 that are due to stretching are degenerate and give rise to a single peak.

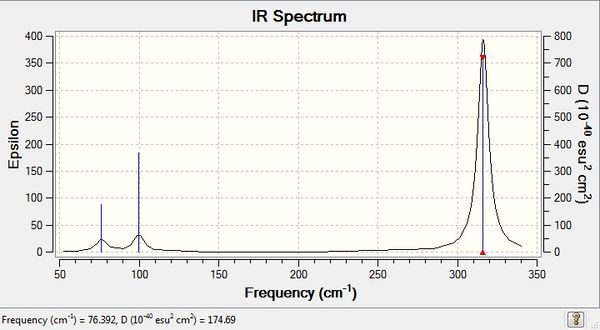
GaBr₃ Frequency Analysis

Frequency file: here D Space DOI:10042/193967


summary data	low modes
	Low frequencies --- -1.4878 -0.0015 -0.0002 0.0096 0.6540 0.6540 Low frequencies --- 76.3920 76.3924 99.6767

Vibrational spectrum for GaBr₃


wavenumber	Intensity	IR active?	type
76	3	yes	bend
76	3	very slight	bend
100	9	very slight	bend
197	0	no	stretch
316	57	yes	stretch
316	57	yes	stretch

|

Similar to BH₃, 3 vibrational peaks are observed when there are 6 vibrations in total. The vibration at frequency 197 cm-1 was not observed as it is not IR active. This is because the asymmetric stretch of all 3 Ga-Br bonds in the trigonal planar, D3h molecule leads to zero change in the molecule's dipole moment and the dipole moments cancel each other out and the molecule is IR inactive. The two vibrations at 76 cm-1 resulting from bending are degenerate and give rise to a single peak. The two vibrations at 316 cm-1 resulting from stretching are degenerate and give rise to a single peak in the spectrum.

   Q:What does the large difference in the value of the frequencies for BH3 compared to GaBr3 indicate?

The values of frequencies for BH3 are in the range of 1162-2716 cm-1 while the values of frequencies for GaBr3 are in the range of 76 to 316 cm-1.The large difference in values for BH₃ compared to GaBr₃ indicate that there is greater displacement from the latter. GaBr₃ has heavier atoms and thus has a greater reduced mass and lower vibrational frequency compared to BH₃. Furthermore, due to the fact that B-H has stronger bonds and greater bond dissociation energy than Ga-Br, it follows that it has greater stiffness constant k and this higher vibrational frequency for a given mode ass according to the simple harmonic motion V=1/2π √(k/µ) , frequency of vibration (V) is proportional to the bond stiffness constant (k) and inversely proportional to the reduced mass (µ).

Q:Looking at the displacement vectors how has the nature of the vibration changed? Why?

The nature of the vibration has changed as for BH₃ the H is the lighter element and thus undergoes umbrella motion, not the central element B. In GaBr₃ it is the central element, Ga that is the lighter element and this undergoes umbrella motion.

Q: There been a reordering of modes! This can be seen particularly in relation to the A2" umbrella motion. Compare the relative frequency and intensity of the umbrella motion for the two molecules.

The reordering of modes can be rationalised considering the relative frequency and intensity of the umbrella motion for the two molecules. GaBr₃ has lower intensity for the umbrella motion than BH₃ due to the fact that Ga is heavier than H. Looking at the bending motions, the intensity is low for both as this involves bringing the atoms together, which leads to repulsion.

   Q:Why must you use the same method and basis set for both the optimisation and frequency analysis calculations?

It is important to use the same basis set for both the optimisation and frequency analysis to maintain the same levels of accuracy throughout the analysis so that the conclusions drawn are not due to differences in basis set used.

Q:What is the purpose of carrying out a frequency analysis?

Frequency analysis allows us to compute the vibrations for the molecule and visualise the bends and stretches and compute a spectrum from the data. It also allows us to confirm that the optimisation was successful and that a minimum structure has been reached. The presence of negative frequencies indicate that this is not the case, as a maximum point is present and that the optimisation was not successful.

   Q:What do the "Low frequencies" represent?

Low frequencies represent the -6 part of 3N-6 vibrational modes for non linear molecules. They are rotations or translations that must be subtracted to obtain the 3N possible vibrations for every degree of freedom. The closer the value to zero, the more accurate the data.

BH₃Molecular Orbitals

D Space DOI:10042/193968

We can see that the real MOs differ from the LCAO MOs.LCAO MOs do not show the interaction between the orbitals and so there is no distortion in their shape. On the other hand real Mos do show the interactions between the orbitals and the degree of bonding overlap and hence we see distortion: bonding interactions occuring through the orbital ovelaps and antibonding when electron density decreases to the point where there is a nodal plane between nuclei. Real MOs help visualize the actual electron density and orbital shape whereas qualitative MO theory often over/underestimates contributions and LCAO Mos do not take into account the interactions between orbitals. With that said, they are a useful tool for small molecules and are good for providing a rough idea.

NH₃ NBO Analysis

NH₃:B3LYP/6-31G (d,p)

The optimisation log file can be found here

Geometry

Summary Data

Convergence Table

Jmol

C_3v

Item               Value     Threshold  Converged?
 Maximum Force            0.000006     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000016     0.001800     YES
 RMS     Displacement     0.000011     0.001200     YES
 Predicted change in Energy=-1.228228D-10
 Optimization completed.
    -- Stationary point found.

NH3 631-G (d,p) optimisation

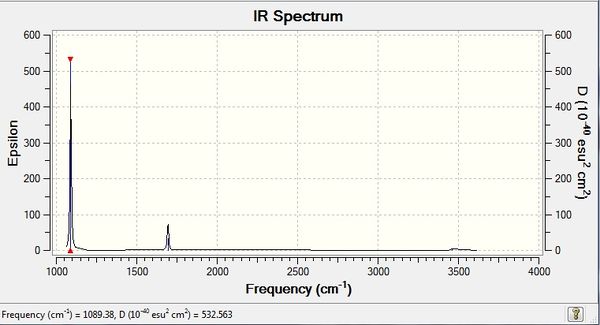
NH₃ Frequency Analysis:B3LYP/6-31G(d,p)

Frequency file: here


summary data	low modes
	Low frequencies --- -0.0129 -0.0027 0.0005 7.0724 8.1020 8.1023 Low frequencies --- 1089.3849 1693.9369 1693.9369

Vibrational spectrum for NH₃


wavenumber	Intensity	IR active?	type
1089	145	yes	bend
1694	14	slight	bend
1694	14	slight	bend
3461	1	no	stretch
3590	0	no	stretch
3590	0	no	stretch

|

NBO Analysis

Population analysis log file here D-Space: DOI:10042/194025

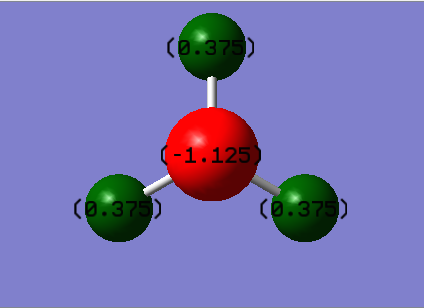
Summary of Natural Population Analysis:                  
                                                         
                                      Natural Population 
               Natural  -----------------------------------------------
   Atom  No    Charge         Core      Valence    Rydberg      Total
-----------------------------------------------------------------------
     N    1   -1.12514      1.99982     6.11104    0.01429     8.12514
     H    2    0.37505      0.00000     0.62250    0.00246     0.62495
     H    3    0.37505      0.00000     0.62250    0.00246     0.62495
     H    4    0.37505      0.00000     0.62250    0.00246     0.62495
=======================================================================
  * Total *    0.00000      1.99982     7.97852    0.02166    10.00000

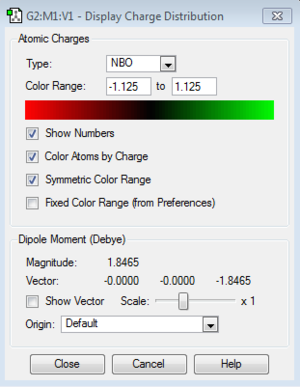
Atom N and H have respective charge distributions -1.125 and 0.375.

NH₃BH₃:B3LYP/6-31G(d,p) level

Optimisation log file here D-space: DOI:10042/194022

Geometry

Summary Data

Convergence Table

Jmol

C_3v

|

        Item               Value     Threshold  Converged?
 Maximum Force            0.000002     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000016     0.000060     YES
 RMS     Displacement     0.000007     0.000040     YES

optimised NHBH molecule

NH₃BH₃ frequency analysis: B3LYP/6-31G(d,p)

Frequency analysis log file here D-Space: DOI:10042/194023


Geometry	Summary Data	Summary Table	Low Frequencies
C_3v	\|	Low frequencies --- -5.5821 -0.2698 -0.0388 0.0008 1.3925 1.4497 Low frequencies --- 263.2918 632.9559 638.4632

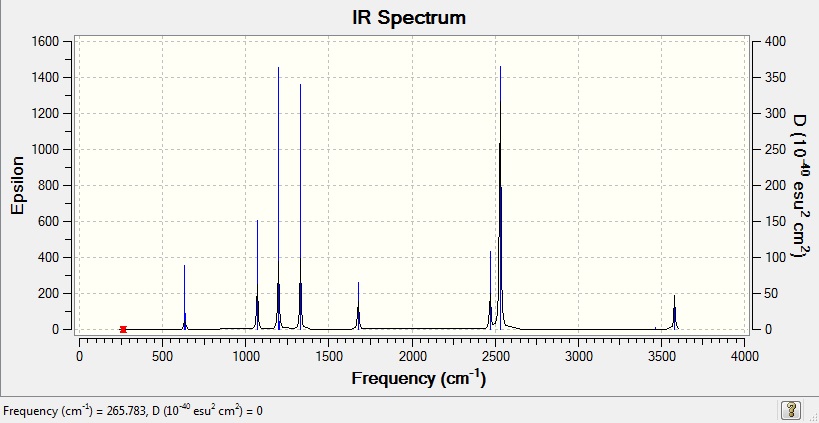
Vibrational spectrum for NH₃BH₃


Wavenumber (cm^-1)	Intensity	IR active?	Type
266	0	no	bend
632	14	slight	stretch
639	4	very slight	bend
639	4	very slight	bend
1069	41	yes	bend
1069	41	yes	bend
1196	109	yes	bend
1204	3	very slight	bend
1204	3	very slight	bend
1329	114	yes	bend
1676	28	slight	bend
1676	28	slight	bend
2470	67	yes	stretch
2530	231	yes	stretch
2530	231	yes	stretch
3463	3	very slight	stretch
3580	28	slight	stretch
3580	28	slight	stretch

Dissociation Energy of the NH₃BH₃ bond

E(NH₃)=-56.5577687 a.u.

E(BH₃)=-26.6153236 a.u.

E(NH₃BH₃)=-83.2246891 a.u.

ΔE=E(NH₃BH₃)-[E(NH₃)+E(BH₃)]=-0.0515968 a.u.=-135.47 kJ/mol

NH3BH3 has bond strength in between a strong bond like a covalent and weak bond like a hydrogen bond- thus is is a medium bond. The figure obtained is in the right ballpark for a bond energy and we would expect a range between 100-500 kj/mol^[4] for a covalent single bond and the figure here is in the right ballpark.

Comment on the dissociation energy

B and N are in the same period of the periodic table and are very similar in size.N is more electronegative than B and this difference contributes some ionic character to the B-N bond which decreases the valence orbital overlap.

Third Year Computational Lab- Part 2: Designer Solvents Mini Project

Ionic Liquids are liquids that comprise of ions. In this project, I shall be utilising computational methods to investigate properties of a selection of cations first through changing the central element, and then in the second part I shall look at the effect of adding electron donating and electron withdrawing groups.

Comparison of Onium Cations

Geometry data
	[N(Me)₄]⁺	[P(Me)₄]⁺	[S(Me)₃]⁺
r(E-Me)/Å	1.51	1.82	1.82
r(C-H)/Å	1.09	1.09	1.09
θ(Me-E-Me)/°	110.0	109.0	102.7
θ(H-C-H)/°	109.5	109.5	109.4

As you can see varying the central atom doesn't change the C-H bond length. The N-C bond is the shortest because N atom is the smallest atom and has shorter covalent radius- therefore it forms shorter and stronger bonds. P-C bond and S-C bond are in the same period of the periodic table and have roughly the same value for bond length. P and S atoms are both larger than N with larger covalent radii and so form longer and weaker bonds. As for the bond angles, the Me-E-Me bond angles are typical for tetrahedral molecules for both [P(Me)₄]⁺ and [N(Me)₄]⁺and as for [S(Me)₃]⁺ the bond angle is smaller. This molecule adopts a trigonal pyramidal structure due to the lone pair on the S. The H-C-H bond angles are roughly the same for all three molecules as there is no distortion in the tetrahedral methyl groups.

[N(Me)₄]⁺:B3LYP/6-31G (d,p)

The optimisation log file can be found here D-Space:DOI:10042/194005

Geometry

Summary Data

Convergence Table

Jmol

T_d

Item               Value     Threshold  Converged?
 Maximum Force            0.000023     0.000450     YES
 RMS     Force            0.000007     0.000300     YES
 Maximum Displacement     0.000042     0.001800     YES
 RMS     Displacement     0.000017     0.001200     YES
 Predicted change in Energy=-7.302671D-09
 Optimization completed.
    -- Stationary point found.

optimised molecule

B3LYP/6-31G(d,p)level

Frequency file: here D-Space:DOI:10042/194008

Table 19: summary of frequency data
summary data	low modes
	Low frequencies --- -0.0010 -0.0005 -0.0003 21.5583 21.5583 21.5583 Low frequencies --- 188.3214 292.5082 292.5082

B3LYP/6-31G(d,p)level

Vibrational Data

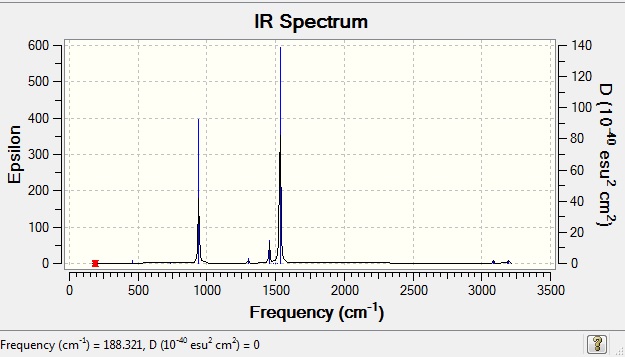
vibrational data
wavenumber	Intensity	IR active?	type
188	0	no	bend
293	0	no	bend
293	0	no	bend
293	0	no	bend
362	0	no	bend
362	0	no	bend
456	0	no	bend
456	0	no	bend
456	0	no	bend
736	0	no	symmetric stretch
941	22	yes (very slight)	bend
941	22	yes (very slight)	bend
941	22	yes (very slight)	bend
1078	0	no	bend
1078	0	no	bend
1078	0	no	bend
1185	0	no	bend
1185	0	no	bend
1306	11	yes (very slight)	bend
1306	11	yes (very slight)	bend
1306	11	yes (very slight)	bend
1456	5	yes (very slight)	bend
1456	5	yes (very slight)	bend
1456	5	yes (very slight)	bend
1487	0	no	bend
1487	0	no	bend
1487	0	no	bend
1502	0	no	bend
1502	0	no	bend
1512	0	no	bend
1532	54	yes	bend
1532	54	yes	bend
1532	54	yes	bend
3087	1	yes (very slight)	stretch (antisymmetric)
3087	1	yes (very slight)	stretch (antisymmetric)
3096	0	no	symmetrical stretch
3189	0	no	symmetrical stretch
3189	0	no	symmetrical stretch
3189	0	no	symmetrical stretch
3190	0	no	symmetrical stretch
3195	1	yes (very very slight)	symmetrical stretch
3195	1	yes (very very slight)	symmetrical stretch
3195	1	yes (very very slight)	symmetrical stretch

IR spectrum

MO Analysis

Orbital Analysis
Orbitals	Comments
	This is completely bonding. The molecular orbital is completely delocalised and the interactions are completely bonding. The interactions are very strong, as there are no nodes and great overlap. The high electronegativity of the central element (nitrogen), means it pulls the electron density more into itself, and hence the orbital is more concave. S-orbitals are responsible for the bonding interactions. \|\|
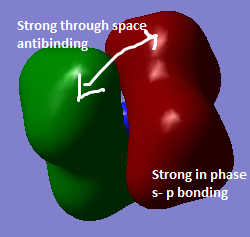	There is strong s-p overlap and 1 internuclear plane at the nitrogen atom. There is less overlap between the orbitals resulting in some strong through space antibonding interactions. Contribution from s orbitals from C and H and p-orbitals from N to bonding.
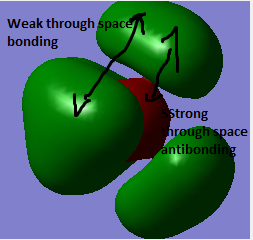	4 nodal planes on each C atom. This orbital has poor overlap between the orbitals which makes it less bonding, However there is strong overlap in the green region resulting in weak through space bonding interactions.
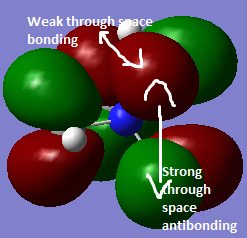	This orbital is less delocalised due to less overlap between the orbitals, relative to orbital's 1 and 2 and hence it is less bonding.However there is some overlap in the green and red regions.
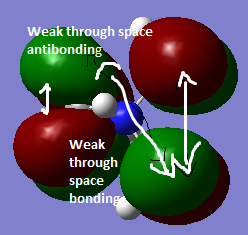	Due to the addition of more nodes, this MO is the least bonding compared to the orbitals above. However, nodal planes contribute less to the antibonding nature of the MO. The level of bonding is relatively less because the main contributions to the bonding is from p-p overlap. There is less s- contribution, therefore not as strong bonding as in the MO's above.This orbital is also less delocalised due to less overlap between the orbitals compared to the orbitals above, so it is the least bonding.

Pop analysis file

D Space:DOI:10042/150542

[P(Me)₄]⁺

B3LYP/6-31G(d,p)level

Optimisation Log file: here D-Space: DOI:10042/194010

Summary of optimisation data

Geometry

Summary Data

Convergence Table

Jmol

T_d

Item               Value     Threshold  Converged?
 Maximum Force            0.000000     0.000015     YES
 RMS     Force            0.000000     0.000010     YES
 Maximum Displacement     0.000001     0.000060     YES
 RMS     Displacement     0.000000     0.000040     YES

optimised molecule

B3LYP/6-31G(d,p)level

Frequency file: here D-Space DOI:10042/194011

Summary of frequency data
summary data	low modes
	Low frequencies --- -0.0009 0.0027 0.0030 24.3438 24.3438 24.3439 Low frequencies --- 159.2180 194.1231 194.1231

IR Analysis

Vibrational data

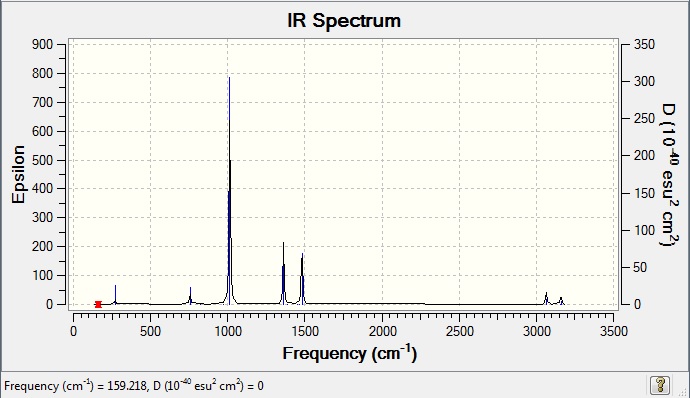
Summary of vibrational data
wavenumber	Intensity	IR active?	type
160	0	no	bend
195	0	no	bend
195	0	no	bend
195	0	no	bend
223	0	no	bend
223	0	no	bend
271	2	yes (very very slight)	bend
271	2	yes (very very slight)	bend
271	2	yes (very very slight)	bend
615	0	no	symmetrical stretch
756	4	yes (very very slight)	bend
756	4	yes (very very slight)	bend
756	4	yes (very very slight)	bend
824	0	no	bend
824	0	no	bend
824	0	no	bend
973	0	no	bend
973	0	no	bend
1013	78	yes	bend
1013	78	yes	bend
1013	78	yes	bend
1362	21	yes	bend
1362	21	yes	bend
1362	21	yes	bend
1389	0	no	bend
1454	0	no	bend
1454	0	no	bend
1454	0	no	bend
1462	0	no	bend
1462	0	no	bend
1481	26	yes	bend
1481	26	yes	bend
1481	26	yes	bend
3064	5	yes (very very slight)	asymmetric stretch
3064	5	yes (very very slight)	asymmetric stretch
3064	5	yes (very very slight)	asymmetric stretch
3066	0	no	symmetric stretch
3157	0	no	symmetric stretch
3157	0	no	symmetric stretch
3158	0	no	symmetric stretch
3158	0	no	symmetric stretch
3160	4	yes (very slight)	symmetric stretch
3160	4	yes (very slight)	symmetric stretch
3160	4	yes (very very slight)	symmetric stretch

MO Analysis

Pop analysis file: DOI:10042/194021

[S(Me)₃]⁺

B3LYP/6-31G(d,p)level

Optimisation file: here D-Space: DOI:10042/194012

Summary of optimisation data

Geometry

Summary Data

Convergence Table

Jmol

 Item               Value     Threshold  Converged?
 Maximum Force            0.000001     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000050     0.000060     YES
 RMS     Displacement     0.000016     0.000040     YES

optimised molecule

B3LYP/6-31G(d,p)level

Frequency file: here D-Space:DOI:10042/194013

Summary of frequency data
summary data	low modes
	Low frequencies --- -6.5180 -6.2165 -6.2124 -0.0030 0.0039 0.0113 Low frequencies --- 163.0240 200.5040 200.5041

Vibrational Data

Summary of vibrational data
wavenumber	Intensity	IR active?	type
162	0	no	bend
200	0	no	bend
200	0	no	bend
255	0	no	bend
255	0	no	bend
285	0	no	bend
624	2	yes (very very slight)	symmetrical stretch
704	1	yes (very very slight)	asymmetrical stretch
704	1	yes (very very slight)	asymmetrical stretch
918	0	no	bend
958	1	yes (very very slight)	bend
958	1	yes (very very slight)	bend
1071	11	yes	bend
1071	11	yes	bend
1076	12	yes	bend
1371	0	no	bend (umbrella motion of 2 methyl group)
1371	0	no	bend (umbrella motion of 2 methyl group)
1408	2	yes (very very slight)	bend (umbrella motion of all methyl group)
1452	0	no	bend (scissoring)
1464	10	yes	bend (scissoring of Me groups)
1464	10	yes	bend (scissoring of Me groups)
1473	25	yes	bend (scissoring of Me groups)
1473	25	yes	bend (scissoring of Me groups)
1485	42	yes	bend (scissoring of Me groups)
3074	0	no	symmetrical stretch
3075	3	yes (very very slight)	asymmetrical stretch
3075	3	yes (very very slight)	asymmetrical stretch
3184	0	no	symmetrical stretch
3185	8	yes	symmetrical stretch
3185	8	yes	symmetrical stretch
3187	3	yes (very very slight)	symmetrical stretch
3187	2	yes (very very slight)	asymmetrical stretch
3187	2	yes (very very slight)	asymmetrical stretch

IR Spectrum

IR spectrum comparison

An interesting observation is that the symmetric stretches increase in frequency on varying the central element. The frequency increases through N to P and then to S. This is similar to what was observed with B and Ga and is due to the increase in atomic size (see discussion of Ga and B IR spectra)

MO Analysis

DOI:10042/194017

NBO Analysis

Charge Distribution
	[N(Me)₄]⁺	[P(Me)₄]⁺	[S(Me)₃]⁺
Charge Distribution range
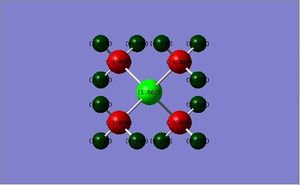
Charge distribution of atoms in molecule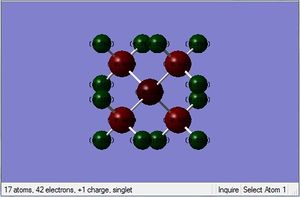

Charge Distribution Data
Atom	[N(Me)₄]⁺	[P(Me)₄]⁺	[S(Me)₃]⁺
C	-0.483	-1.05	-0.847
H	0.269	0.298	0.297
X	-0.295	1.667	0.919

NBO Analysis
	[N(Me)₄]⁺	[P(Me)₄]⁺	[S(Me)₃]⁺
Contribution from Carbon (%)	34	60	49
Contribution from Heteroatom (%)	66	40	51

Discussion

Looking at the charge distribution, carbon has the most electron density. This can be rationalised by considering the adjacent heteroatoms and their electronegativity relative to carbon. Although this is the case, the charge distribution goes against what we might expect, as carbon is more electron dense despite N being more electronegative. We can rationalise this by considering the neighbouring H atoms, in the C-H bond the carbon is more electronegative than hydrogen and this draws electron density towards the carbon atom.

Looking at the relative contributions we would expect the more electronegative atom to contribute most. This is indeed that case as we can see from the table. P contributes least to the C-X bond as it is less electronegative than C and this is also true for S. The results of the table of relative contributions, we would expect N to have the most negative charge however this is not the case, and infact C has the most negative charge despite N having the greatest contribution. This can be rationalized by considering the 3 neighboring H atoms which draw electron density towards the carbon. P is the most positive of the heteroatoms, followed by S. This can be explained as it contributes least to the C-X bond compared to N and S. P is also the least electronegative of the three. S is also partially positive, although less positive than P and again this can be explained because it contributes more to the C-X bond than P although both contribute less to the bond than carbon.

In general, as the charge on central atom decreases, the contribution of the central atom to the bond would increase. The charge on C atom is always negative in all 3 cases.

Traditional theory depicts the partial positive charge on the N atom when in reality this is shared between the H atoms. In N(CH₃)₄]⁺, the N atom has a slight negative charge of -0.29 which is inconsistent with the traditional theory and mechanism which predicts the positive charge on the N following donation of the lone pair. This discrepancy could be explained due to the high electronegativity of N. The charge distribution shows that the hydrogen atoms actually bear the positive charge not the nitrogen atom and this can be explained by the fact that the electrons in the C-H bond are drawn to the more electronegative carbon, and the carbon has its electrons drawn towards the more electronegative N atom in the C-N bond which leaves the H partially positive. Therefore the positive charge is actually shared between the 3 H atoms.

Discussion on [NR₄]⁺ (R=alkyl)

[NR₄]⁺ is traditionally depicted with a positive charge on N atom. Most mechanisms show that this species is obtained by the donation of a lone pair of electrons from NR3 to an alkyl group with one positive charge, forming a dative bond. As a result, 2 electrons in the new bond,would be equally shared between N and C atom, so the N atom would be short by one electron hence the positive charge would be placed on the N atom. However, the computational calculation indicated that the formal positive charge should be delocalised over all the H atoms since H atoms are the most electropositive atoms in this kind of species as shown through the NBO analysis. This discrepancy between traditional theory and the computational result can be accounted for as the computational methods take into account the relative electronegativities of the atoms.

Part 2: Influence of functional groups

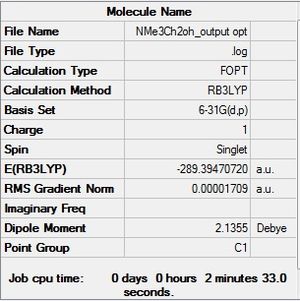
[N(Me)₃(CH₂OH)]⁺

Final Optimisation File: here D-Space: DOI:10042/194018

Summary of optimisation data

summary data

convergence

Jmol


         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000015     YES
 RMS     Force            0.000001     0.000010     YES
 Maximum Displacement     0.000016     0.000060     YES
 RMS     Displacement     0.000006     0.000040     YES

optimised molecule

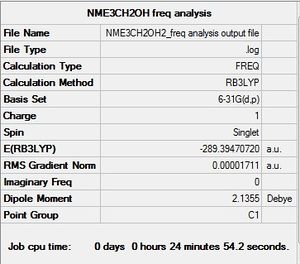
B3LYP/6-31G(d,p)level

Frequency file here: here

D-Space: DOI:10042/194019

Summary of frequency data
summary data	low modes
	Low frequencies --- -7.7885 -4.7712 -0.0004 0.0001 0.0008 2.9554 Low frequencies --- 131.2033 213.5539 255.6828

MO Analysis

Pop analysis file: DOI:10042/194020

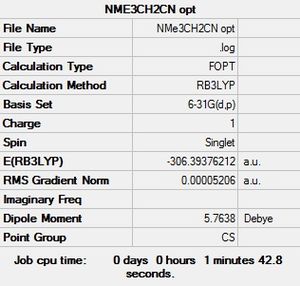
[N(CH₃)₃(CH₂CN)]⁺

B3LYP/6-31G(d,p)level

Optimisation file: here D-Space: DOI:10042/194014

Summary of optimisation data

summary data

convergence

Jmol

 Item               Value     Threshold  Converged?
 Maximum Force            0.000009     0.000015     YES
 RMS     Force            0.000003     0.000010     YES
 Maximum Displacement     0.000052     0.000060     YES
 RMS     Displacement     0.000015     0.000040     YES

optimised molecule

[N(CH₃)₃(CH₂CN)]⁺

B3LYP/6-31G(d,p)level

Frequency file: here D-Space: DOI:10042/194015

Summary of frequency data
summary data	low modes
	Low frequencies --- -3.4483 0.0005 0.0006 0.0010 4.3524 5.5928 Low frequencies --- 92.1416 154.3245 212.1231

MO Analysis

DOI:10042/194016

NBO Analysis

NBO Analysis of [N(Me)₃CN]⁺ and [N(Me)CH₂OH]⁺
	[N(Me)₃CN]⁺	[N(Me)CH₂OH]⁺
Charge Distribution range
Charge Distribution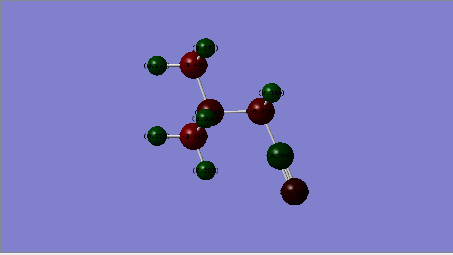

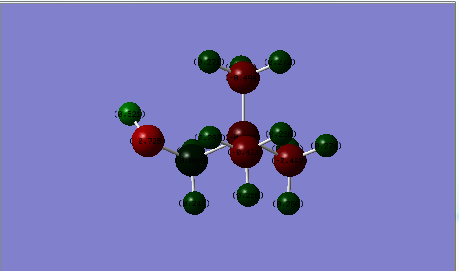
Charge Distribution Table

Cation	Charge on N atom	Charge on C atoms	Charge on H atoms	Charge on O atom
[N(CH₃)₃(CH₂OH)]⁺	-0.322 central atom	0.088 ('CH₂OH), -0.491 ~ -0.494 (CH₃)	0.521 (OH), 0.237, 0,249 (CH₂OH), 0.262-0.282 (CH₃)	-0.725
[N(CH₃)₃(CH₂CN)]⁺	-0.289 central atom, -0.186(CN)	-0.358(CH₂CN),0.209, (CN), -0.358 ~-0.489 (CH₃	0.269-0.282 (CH₃, 0.309 (CH₂CN)	N/A
[N(CH₃)₄]⁺	-0.295 central atom	-0.483	0.269	N/A

HOMO/LUMO

Energies

HOMO/LUMO comparison
	[N(Me)₄]⁺	[N(CH₃)₃(CH₂OH)]⁺	[N(CH₃)₃(CH₂CN)]⁺
HOMO
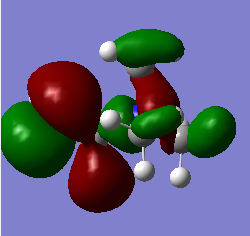LUMO

Energy Analysis
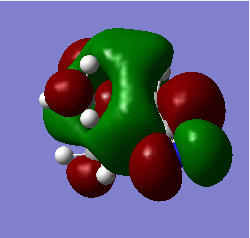
Molecule	HOMO (A.U.)	LUMO (A.U.)	Energy Gap (A.U.)
[N(CH₃)₄]⁺	-0.57933	-0.13308	0.44626
[N(CH₃)₃(CH₂OH)]⁺	-0.48765	-0.12460	0.36302
[N(CH₃)₃(CH₂CN)]⁺	-0.50049	-0.18182	0.31862

Q OH is an electron donating group and CN is an electron withdrawing group, What effect have these groups had on the charge distribution?

The electron withdrawing CN group has drawn electron density away from the adjacent carbons and this is shown when comparing the charges of the adjacent carbons: the methyl groups in proximity to the CN are more positive than those in proximity to the OH. The methyl carbons in proximity to the OH group are actually more negative than those in [N(CH₃)₄]⁺ which highlights the electron donating effects of the OH group. It is interesting to see however, that the OH also draws electron density away from the adjacent carbons as these are most positive at 0.08. This is because although OH group is electron donating through resonance, it is inductively electron withdrawing and draws electron density away from the carbons directly adjacent to this group.

Q Compare and contrast the HOMO and LUMO of[N(CH₃)₄]⁺ [N(CH₃)₃(CH₂OH)]⁺ and [N(CH₃)₃(CH₂CN)]⁺ has the energy of these orbitals moved?

The HOMO-LUMO gap decreased with the addition of the CN and OH groups respectively. This makes electron promotion from HOMO - LUMO easier and increases the reactivity of the molecule. [N(CH₃)₄]⁺ is the most stable as it has the largest HOMO-LUMO gap. The HOMO goes up for both OH and CN groups and this could be due to the increase in antibonding interactions.

Q How has the shape of the orbitals changed?

We can see that [N(CH₃)₄]⁺ has the most stable HOMO as it has the most bonding interactions. The HOMOs for [N(CH₃)₃(CH₂OH)]⁺ and [N(CH₃)₃(CH₂CN)]⁺ are less stable in comparison due to the increase in antibonding interactions and with the HOMO of [N(CH₃)₃(CH₂OH)]⁺ being highest in energy as it has the most nodes. The LUMO of [N(CH₃)₄]⁺ is also the most stable as it is the most delocalised and has greater overlap. The LUMOs of the most electrom withdrawing groups are lowering in energy which is why [N(CH₃)₃(CH₂CN)]⁺ 's LUMO is lower in energy than the LUMO of [N(CH₃)₃(CH₂OH)]⁺. This also decreases the HOMO-LUMO gap and explains why [N(CH₃)₃(CH₂CN)]⁺ is the most reactive.

Q What chemical impact could these changes have?

These changes can affect the chemical reactivity of a molecule:the smaller the energy gap between the HOMO and the LUMO, the more reactive the molecule. In this case, [N(CH₃)₃(CH₂CN)]⁺ has the smallest HOMO- LUMO gap and so is the most reactive of the three.

Conclusion

In conclusion we have utlised various computational methods to analyse small molecules. It has been shown that using a higher basis set increases the accuracy of calculations. We have also seen the effects of changing both the central atom and ligands on physical properties of bonds and angles. In the mini project: Ionic Liquids, we have utlised computational methods to analyse small cations and have investigated the effects of adding electron donating and electron withdrawing groups to [NME4]⁺.

Acknowledgements

I would like to thank Dr Patricia Hunt for her guidance and advice throughout this project. I would also like to thank all the demonstrators,Bryan Ward and Precious Ugbogmah, for their help and support.

References

[1] http://staff.ustc.edu.cn/~luo971/2010-91-CRC-BDEs-Tables.pdf

[2] http://www.huntresearchgroup.org.uk/teaching/year2_mos.html#lecture4

[3] http://www.wiredchemist.com/chemistry/data/bond-energies-lengths

[4] Pauling, L. (1960) The Nature of the Chemical Bond. Cornell University Press. p.340-354

[5]Blanksby, S. J.; Ellison, G. B.; (2003). "Bond Dissociation Energies of Organic Molecules". Acc. Chem. Res. 36 (4): 255–263. doi:10.1021/ar020230d. PMID 12693923.

Third Year Computational Lab- Part 1

EX3 Section

BH3:B3LYP/3-21G

Optimization log file

BH3:B3LYP/6-31G (d,p)

GaBr3:B3LYP/LANL2DZ

Optimization log file

BBr3:B3LYP/6-31G(d,p)LANL2DZ

Optimization log file

Further Optimisation

BH3 Frequency Analysis:B3LYP/6-31G(d,p)

Vibrational spectrum for BH3

GaBr3 Frequency Analysis

Vibrational spectrum for GaBr3

BH3Molecular Orbitals

NH3 NBO Analysis

NH3:B3LYP/6-31G (d,p)

NH3 Frequency Analysis:B3LYP/6-31G(d,p)

Vibrational spectrum for NH3

NBO Analysis

NH3BH3:B3LYP/6-31G(d,p) level

NH3BH3 frequency analysis: B3LYP/6-31G(d,p)

Vibrational spectrum for NH3BH3

Dissociation Energy of the NH3BH3 bond

Comment on the dissociation energy

Third Year Computational Lab- Part 2: Designer Solvents Mini Project

Comparison of Onium Cations

[N(Me)4]+:B3LYP/6-31G (d,p)

B3LYP/6-31G(d,p)level

B3LYP/6-31G(d,p)level

Vibrational Data

IR spectrum

MO Analysis

Pop analysis file

[P(Me)4]+

B3LYP/6-31G(d,p)level

B3LYP/6-31G(d,p)level

IR Analysis

Vibrational data

MO Analysis

[S(Me)3]+

B3LYP/6-31G(d,p)level

B3LYP/6-31G(d,p)level

Vibrational Data

IR Spectrum

IR spectrum comparison

MO Analysis

NBO Analysis

Discussion

Discussion on [NR4]+ (R=alkyl)

Part 2: Influence of functional groups

[N(Me)3(CH2OH)]+

B3LYP/6-31G(d,p)level

MO Analysis

[N(CH3)3(CH2CN)]+

B3LYP/6-31G(d,p)level

[N(CH3)3(CH2CN)]+

B3LYP/6-31G(d,p)level

MO Analysis

NBO Analysis

Charge Distribution Table

HOMO/LUMO

Energies

Conclusion

Acknowledgements

References

EX₃ Section

BH₃:B3LYP/3-21G

BH₃:B3LYP/6-31G (d,p)

GaBr₃:B3LYP/LANL2DZ

BBr₃:B3LYP/6-31G(d,p)LANL2DZ

BH₃ Frequency Analysis:B3LYP/6-31G(d,p)

Vibrational spectrum for BH₃

GaBr₃ Frequency Analysis

Vibrational spectrum for GaBr₃

BH₃Molecular Orbitals

NH₃ NBO Analysis

NH₃:B3LYP/6-31G (d,p)

NH₃ Frequency Analysis:B3LYP/6-31G(d,p)

Vibrational spectrum for NH₃

NH₃BH₃:B3LYP/6-31G(d,p) level

NH₃BH₃ frequency analysis: B3LYP/6-31G(d,p)

Vibrational spectrum for NH₃BH₃

Dissociation Energy of the NH₃BH₃ bond

[N(Me)₄]⁺:B3LYP/6-31G (d,p)

[P(Me)₄]⁺

[S(Me)₃]⁺

Discussion on [NR₄]⁺ (R=alkyl)

[N(Me)₃(CH₂OH)]⁺

[N(CH₃)₃(CH₂CN)]⁺

[N(CH₃)₃(CH₂CN)]⁺