Rep:Mod:nsolomon3

Updates

• • The problem Mod:nfs08updates has been resolved as of 19.00 22/01/11. Any changes that have been made after 5pm 18/02/11 have only been to upload DOIs/log files. These have all been uploaded now.***

Objectives

This computational experiment aims to characterise transition structures on potential energy surfaces for the Cope rearrangement and Diels Alder cycloaddition reactions. Molecular orbital-based methods to numerically solving the Schrödinger equation and find the transition structures on potential energy surfaces will be used. This proves very powerful as reaction paths and activation energies for particular reactions can be calculated. The Hartree-Fock approximation methods will be primarily used as they are well suited for this level of structural complexity. In various instances a comparison will be made to the higher level density functional approach chiefly involving the B3YLP method and 6-31G* basis set. Discussion of these semi-empirical quantum mechanical methods has already taken place in Mod:nsolomon1 and Mod:nsolomon2 The user-friendly interface Gaussview and program Gaussian will be used to view and process calculations.

Part 1 - The Cope Rearrangement

Conformations of 1,5 hexadiene

(a) - (e)

We will first optimise the structures under the Hartree-Fock (HF) ab initio approximation. This is a purely theoretical approach in contrast to density functional theory (DFT) which is based on a series approximations used to match experimental evidence. The initial basis set used under HF will be 3-21G; this is a fairly small basis set used for quick calculations to gain an understanding of simple molecules.

We will adopt a convention of labelling the carbon atoms from left to right (1 to 6). For the gauche conformations we adopt a 60° between the ethylene substituents and for the anti arrangement we adopt 180°. We will then introduce variations in these structures to form different conformers by rotation the ethylene groups. Analysing the HF/3-21G energy calculations we find the the gauche 3 conformation is the most stable. We may attribute this to three general factors which are recurrent throughout the analysis.

1) Maximising the number pp hyper conjugative overlaps of σ* orbitals (C-H or C-C) with σ orbitals (C-H or C-C); this is usually achieved by having two gauche susbsituents (known as the gauche effect) which contradicts the expected steric hinderance which would otherwise raise the energy.
2) Minimising the repulsion of two σ orbitals; this is usually observed with two pp substituents.
3) The Van der Waal effect: This is when two atoms are located at a distance apart that maximises the Van der Waal attraction. For H-H interactions this is 2.4-2.6 Å and for C-H this is ca 2.7-2.8 Å.

The energies and structures calculated of the conformers match those in Appendix 1 exactly.

Conformer	Structure	Point Group	Energy/Hartrees HF/3-21G	Relative Energy/kJ/mol	Energy/Hartrees DFT/6-31G*	Relative Energy/kJ/mol
gauche1	Molecule 9	C2	-231.69153 DOI:10042/to-7237	2.97	-234.61048 DOI:10042/to-7240	3.46
gauche2	Molecule 9	C2	-231.69167 DOI:10042/to-7242	2.59	-234.61068 DOI:10042/to-7243	2.93
gauche3	Molecule 9	C1	-231.69266 DOI:10042/to-7245	0.00	-234.61133 DOI:10042/to-7244	1.24
gauche4	Molecule 9	C2	-231.68772 DOI:10042/to-7247	12.97	-234.60788 DOI:10042/to-7248	10.31
anti1	Molecule 9	C2	-231.69260 DOI:10042/to-7250	0.18	-234.61180 DOI:10042/to-7252	0.00
anti2	Molecule 9	C1	-231.69097 DOI:10042/to-7254	4.48	-234.61079 DOI:10042/to-7253	2.66
anti3	Molecule 9	C2h	-231.68907 DOI:10042/to-7257	10.83	-234.60962 DOI:10042/to-7258	5.72
anti4	Molecule 9	Ci	-231.69254 DOI:10042/to-7256	0.39	-234.61170 DOI:10042/to-7259	0.26

For the gauche 3 conformer we observe three H-H interactions across the two central carbons (3 and 4) at a distance of 2.53Å and 2.41Å which is energetically attractive. We also observe a distance of 2.84/2.86 Å separating carbon 2 and 5 from hydrogens on the central carbon atoms (3 and 4). Across carbons 3 and 4 we also see four anti-periplanar relationships. This leads to good overlap of the σ_CH with the σ*_CC. Very close to this we see the anti 1 conformer we see similar H-H gauche interactions but importantly the confomrer exhibits 4 app overlaps across carbons 3 and 4. This is σ_CC-σ*_CC interaction. The two interactions are so close in energy, 0.18kJ/mol apart, that we conclude that they are essentially equally low in energy. We may use similar arguments for the anti 4 conformer, 0.39kJ/mol above the gauche 3.

The gauche 2 is 2.59kJ/mol above gauche 3; we may rationalise this by considering the Van der Waal interaction. The distance between the hydrogen on carbon 2 and atom carbon 4 is 2.82Å and to carbon 5 it is 3.44Å which means that we are further away from the minimum of the potential well for the Van der Waal attraction. Similar arguments can be used for the gauche 1 conformation 2.97kJ/mol greater than gauche 3.

When considering the anti4 confromation, 4.48kJ/mol higher in energy than the gauche 3 conformation, on the onset there appears to be no apparent reason for the discrepancy as there equal number of favourable Van der Waal attractions (within 2.4 Å). To explain this we must take a more sophisticated MO approach. As can be seen in the diagrams below the gauche 3 conformation has, overall, a more bonding interaction as can be seen by the extension of the π bond across both double bonds. This is not observed nearly as much in the anti 2 conformation. As for the anti 3 and the gauche 4 conformations we see that they are 10.83 and 12.97 kJ/mol higher in energy than the gauche 3. This may be attributed to the repulsive antibonding interactions observed across the two central carbons. The effect happens to be greater for the gauche 4 conformation, primarily due to sterics. Interestingly the order of energies for anti2, anti3 and gauche 4 mirrors the absolute energies of the HOMOs (-0.36029, -0.35810 and -0.34768 a.u. respectively).

HOMOs: Conformers 1,5 hexadiene

gauche 3	anti2	anti3	gauche4

(f)-(g)

We will no extend the level of theory to the more sophisticated DFT calculation with a B3YLP method and 6-31G* basis set. Note the * indicates that we include the d-orbital contributions to the overall energy. This will allow our basis set to "better fit" the "floppy" nature of the molecule. The results are summarised in the above table.

Focusing on the anit4 conformation with Ci symmetry we observe subtle structural changes when applying the DFT calculation. The C-C bond length decreases from 1.51 to 1.50 Å and the C=C from 1.33 to 1.32 Å. The C-C=C angel moves insignificantly from 124.78 to 125.28°. These small changes in the geometry indicate that the HF method is very comparable to using the DFT method for structural properties of simple molecules. However the energy calculations indicate a different relative order for the conformers.

Gauche3 DFT calc.

Now denoting gauche=g and anti=a, we see that the lowest three conformers g3, a1 and a4 are now ordered a1,a4, and g3. The ordering observed after the DFT calculation for a1 and a4 can most probably be attributed to the error in the calculation (difference is 0.26kJ/mol). However, g3 which is higher than a1 by 1.24 kJ/mol may be attributed to an extra bonding interaction observed in the HOMO of the molecule. This is due to the additional functions included in the basis set. A similar MO argument can be used to rationalise the change in ordering for the next set of 3 conformers. i.e g2,g1 and a2 changes to a2,g2 and g1.

We will now run frequency calculations to confirm that we are indeed at a minimum. The frequency is essentially the second derivative of the potential energy surface and all positive frequencies will indicate that we are essentially at the minimum of the potential energy well and not at a transition state maximum. It is important that we use the same method and basis set to confirm the minima. These modes have been calculated and can be viewed in Gaussview:

Notice that in the .log output file we observe 6 "low frequencies" which are not classified as "real" vibrational frequencies as they correspond the the 3 degrees of freedom in translational and rotational motion. We can also extract vital information regarding the different types of energy of the molecule to enable comparison to the appropriate energy in the literature:

(i) "the sum of electronic and zero-point energies" corresponds to the potential energy at 0K + Zero pt. energy
(ii) "the sum of electronic and thermal energies" corresponds to the energy (1atm, 298.15K) inc. translational, vibrational and rotational contributions
(iii) "the sum of electronic and thermal enthalpies" effectively includes RT correction
(iv) "the sum of electronic and thermal free energies" is an effective freee energy, G = H - TS

These will prove useful in subsequent calculations.

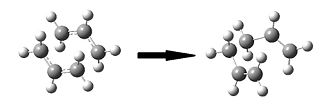
Optimizing the "Chair" and "Boat" Transition Structures

We will now try to model the two different transition states for the Cope rearrangement shown in Appendix 2. First we will need to establish a transition structure optimization by computing the force constants at the beginning of the calculation. The force constant is essentially the second derivative under the harmonic approximation that we are looking for. We are moving up the potential energy well this time until we reach a maximum (negative force constant)

(a)-(b)

A CH2CHCH2 and fragment is firstly optimized using the HF/3-21G method and basis set: DOI:10042/to-7306 . This is then copied and aligned as per the transition state shown in Appendix 2. We will firstly try to compute Hessian force constant matrix and optimise it to a transition state (Berny). The additional keyword Opt=NoEigen is added to prevent the calculation from crashing when the imaginary frequency is found. This method is carrying out two key parts to the calculation simultaneously: i) varying the distance between the fragments and ii) optimising the remaining part of the molecule. We will see later that it is not advantageous to choose this method as the calculations can get quite complex, especially for larger molecules. The result is a negative (imaginary) frequency at 818cm^-1 indicating the presence of a transition state. The resultant fragments have end to end distance of 2.02 Å and energy -231.6193 a.u.

1,5 hexadiene: chair TS DOI:10042/to-7307

chair_TS	Vibration

(c)-(d)

We will now adopt a different approach to computing the transition state. Firstly the coordinates will be freezed so that the molecule is 2.20 Å apart and the rest of the structure relaxed to move from the planar (input) fragments to slightly distorted out of plane fragments DOI:10042/to-7308 , DOI:10042/to-7309 :

chair_following_freeze

As can be seen the hydrogens are out of plane and point away from one another when considering both fragments. The structure has been relaxed and the inter-fragment length fixed at 2.20 Å. Now we will vary the distance between the two fragments and find search for the local maximum along the potential energy well.

The distance between the two fragments is 2.02 Å as calculated earlier using the method involving solely optimisation of the Hessian. This is an important verification that the result from both methods is identical, except as mentioned, the first method may take longer fore more complex molecules especially if the starting geometry is far from the transition state. The imaginary frequency is also 818cm^-1. The absolute energy is as expected equal to -231.6193 a.u. indicating that both methods give the same results.

(e)

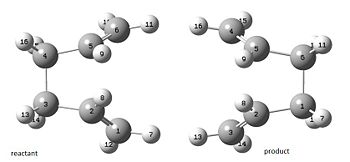
We will now attempt to optimise the "boat" transition structure using the QST2 method. Importantly we must pay special attention to the numbering of our atoms to ensure the numbering in the reactants matches that in the products. Hence:

Labelling 1,5 hexadiene

atomic labels	atomic lables

It turns out that with the current starting geometries the job fails DOI:10042/to-7310 . This highlights how much Gaussian relies on reasonable inital geometry. By inspection of the output file we see a distorted chair like structure. It is clear the one allyl fragment has simply been translated over the other and rotation about the central C-C bond has not been considered. We therefore choose to change the C2-C3-C4-C5 dihedral angle to 0o and the C2-C3-C4 and C3-C4-C5 angle to 100o and re-run the job.

Error output structure and new starting conformer: 1,5 hexadiene

chair_TS_error	boat rotated

The structure has converged to the boat transition structure with one imaginary frequency at 840cm^-1 and absolute energy of -231.6080 a.u. which is 30kJ/mol higher than the chair transition state DOI:10042/to-7311 . The reason for this is that in the chair structure the axial hydrogens are alternative and in the boat they are adjacent giving rise to a higher energy flagpole interaction. The literatre reports the energy difference is 45kJ/mol which is not too far from our estimate.

1,5 hexadiene: boat TS

boat_TS	Vibration

(f)

By solely considering the transition structures it is next to impossible to predict which conformers they lead to. We may loosely say that the chair state will lead to gauche 2 and the boat to gauche 3. We can verify this by computing the intrinsic reaction coordinate. Note: had time allowed computation using the more reliable QST3 method would have take place.

Intrinsic Reaction Coordinate (IRC) method

(f)-(g)

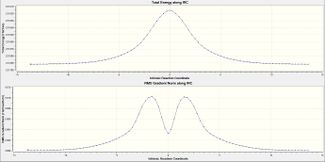
The IRC method allows us to follow the minimum energy path starting from the transition state structure to the minimum of the potential energy well. A series of points is created and the geometry is changed such that a move is made down the steepest (negative gradient) part of the slope. As the reaction is symmetrical we will only compute the IRC in the forward direction. We begin by considering 50 points along the IRC path.

IRC Chair 1,5 hexadiene DOI:10042/to-7296

IRC chair	RMS grad. chair	Start to end

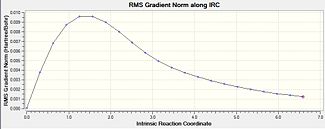The structure begins at -231.6193 a.u and after 22 steps move down 175kJ/mol to -231.6860 a.u. This energy change is of reasonable order of magnitude. However this is not the energy minimum expected as the RMS gradient ends at 0.0012, which on a computational level, is not close enough to zero.

The corresponding IRC for the boat is shown below:

IRC Boat 1,5 hexadiene DOI:10042/to-7297

IRC boat	RMS grad. boat	Start to end

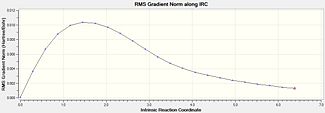The structure begins at -231.6028 a.u and after 22 steps move down 189kJ/mol to -231.6751 a.u. Similarly, this is not the energy minimum expected as the RMS gradient ends at 0.0012, which on a computational level, is not close enough to zero.

With the number of points chosen we have not yet reached the minimum geometry. To find the minimum geometry from the current lowest energy structure we can do one of three things:

(i) run a simple minimisation from where the IRC method ended. However this has the disadvantage that the wrong minimum may be computed if we begin far from the minimum required. (ii) re-run the IRC calculation specifying a larger number of points, say 200. However, if too many points are requested deviation from the required structure occurs.
(iii) re-run the IRC method, except this time compute the force constants at every step of the calculation. Often this is the most reliable out of the three except that it is not so feasible for larger systems.

We will investigate the effect of the the above changes.

Modification (i), (ii), (iii) summary

Modification:	Energy minimisation (i)	Increase to 200 steps (ii)	Force constants (iii)
Chair	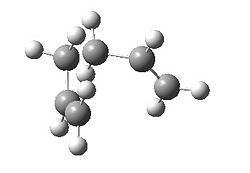E=-231.6917 a.u. DOI:10042/to-7312	-231.6860 a.u. DOI:10042/to-7298	-231.6917 a.u. DOI:10042/to-7300
Boat	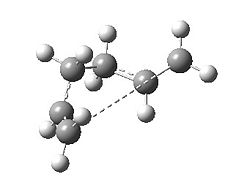E=-231.6927 a.u. DOI:10042/to-7313	-231.6750 a.u. DOI:10042/to-7299	-231.6857 a.u. DOI:10042/to-7301

Following (i) minimisation we observe that the minimum for the chair transition corresponds to the gauche 2 structure above with C2 symmetry and has identical energy of -231.6917 a.u. As for the boat, the energy is -231.6926 a.u. which is 2.4kJ/mol lower in energy than the product from the chair transition state. In fact, this corresponds to the gauche 3 structure above with C1 symmetry. By applying (ii), the 200 step cycle, the energies for the chair and boat pathway minima are -231.6080 and -231.6751 a.u. as expected as the process was only a 22 step process. By applying (iii) for chair, the run ends in 47 steps with energy -231.6917 a.u. which is identical to the minimisation indicating the effectiveness of this method. For the boat, the run ends in 52 steps with energy -231.6857 a.u. which like the chair, is identical to the minimisation carried out above.

(g)

We will now attempt to estimate the activation energies to these transition states at 298.15K and 350.0K. We will optimise the transition states using the B3YLP/6-31G* level of theory to enable comparison to the HF/3-21G level. The results are summarised below and are consistent with those in Appendix 2:

[Note: the utility program FreqChk was used to correct the energy for the higher temperature of 350.0 K. Also, a good control is to take one of the structures, say the (HF calc.)anti 4 conformation, and calculate the energies at 0K and 0.0 atm. The corrections to the "Sum of electronic and zero-point energies" and "Sum of electronic and thermal energies" should be the same as there is no thermal energy at 0K and 0.0 atm. This was carried out and all the corrections had equal value of 0.152995 a.u.]

Summary of energies (in hartree)

	HF/3-21G DOI:10042/to-7307 DOI:10042/to-7311 DOI:10042/to-7314				B3LYP/6-31G* DOI:10042/to-7302 DOI:10042/to-7303
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K	at 350 K		at 0 K	at 298.15 K	at 350 K
Chair TS	-231.619322	-231.466700	-231.461346	-231.459446	-234.556983	-234.414929	-234.408998	-234.406899
Boat TS	-231.602802	-231.450927	-231.445300	-231.443348	-234.543093	-234.402342	-234.396006	-234.393798
Reactant (anti4)	-231.692535	-231.539540	-231.532566	-231.530482	-234.611710	-234.469212	-234.461856	-234.459589

Summary of activation energies (in kcal/mol)

	HF/3-21G	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 350 K	at 0 K	at 298.15 K	at 350 K	at 0 K
ΔE (Chair)	45.70	44.69	44.58	34.06	33.17	33.06	33.5 ± 0.5
ΔE (Boat)	55.60	54.76	54.68	41.96	41.32	41.28	44.7 ± 2.0

The first observation to be made is that the activation energy via the boat transition state is 0.1 kcal/mol higher in energy than proceeding via the chair for the HF/3-21G; for the B3YLP/6-31G* this is 0.7-0.8 kcal/mol. We may initially suspect that these small energy differences are within the computational error of the experiment, however as we are comparing the energies relative to one another the error is effectively cancelled out. The sum of electronic and thermal energies includes the zero-point energy and is essentially a raw energy considering the effect of temperature (a function kinetic energy) in the system. Increasing the temperature from 0K --> 298.15 K --> 350.0 K decreases the activation energy, even if by a very small amount.

Part 2 - The Diels Alder Cycloaddition

In this part we will investigate the transition structures of two Diels-Alder reactions. Diels-Alder reactions are pericylic reactions where π orbitals of dieneophiles are used to form new σ bonds with the π orbitals of the dienes. Regioselectivity issues arise when considering the orbital overlaps or steric repulsions in many systems. In particular for the reaction of cyclohexa-1,3-diene reaction with maleic anhydride we will aim to predict the regioselctivity of the products chiefly based on MO considerations of the transition states. Two key requirements are needed for a Diels-alder reaction: i) There must be a HOMO from one reactant interacting with the LUMO from the other. ii) This interaction is only allowed if the orbitals are of identical symmetry.

We will use AM1 semi-empirical molecular orbital method for these calculations as they are quick and prove effective from reasonably simple pericylic reactions. Extension to more advance DFT-methods will be carried out should time permit.

Prototype reaction

We begin by considering the [4s + 2s] cycloaddition of ethylene to 1,3 cis-butadiene:

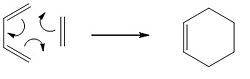
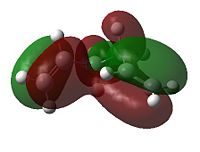
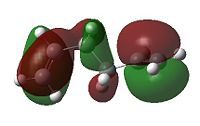
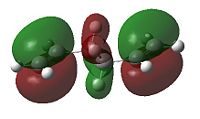
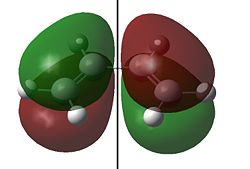
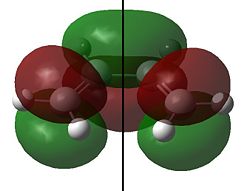
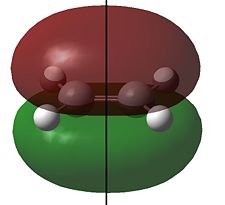
The HOMO and LUMO for cis-butadiene and ethylene are shown below:

AM1 optimisation - HOMO-LUMO cis-butadiene/ethylene DOI:10042/to-7315 DOI:10042/to-7316

HOMO cis-butadiene, E= - 0.34382 a.u.	LUMO cis-butadiene, E = 0.01709 a.u.	HOMO ethylene, E = -0.38777 a.u.	LUMO ethylene, E = 0.05284 a.u.

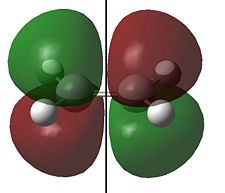Clearly the for cis-butadiene the HOMO is antisymmetric (a) and the LUMO is symmetric (s) with respect to the plane of symmetry shown; we have the opposite situation for ethylene. As we can pair up the HOMO from one molecule with the LUMO from the other by symmetry (i.e. both s or a) the reaction is allowed. We can therefore expect an interaction between the HOMO of butadiene with the LUMO of ethylene and an interaction of the HOMO of ethylene with the LUMO of butadiene and the

Computation of the Transition State geometry for the prototype reaction and an examination of the nature of the reaction path

The optimised fragments were taken and arranged as shown below with initial separation between the terminal carbons of about 2.0 Å. The semi-empirical AM1 method was used initially and then investigation with the higher level DFT-B3YLP/6-321G* method and basis set took place. The results are summarised below.

Summary TS (Berny)

Method	Structure	Animation	Frequency/cm-1
Semi-empirical AM1 DOI:10042/to-7317	Separation = 2.12 Å, C=C = 1.38 Å, C-C = 1.40 Å	Vibration	- 956
DFT-B3YLP/6-321g* DOI:10042/to-7295	Separation = 2.27 Å, C=C = 1.38 Å, C-C = 1.41 Å	Vibration	- 524

1st Positive freq. twist

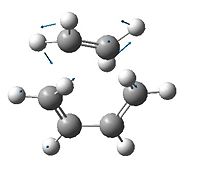
The imaginary frequency at -956cm^-1 for the for the semi-empirical AM1 method and -524cm^-1 for the DFT method indicates that we have a transition state where the bond forming is synchronous; comparison with the the 1st positive frequency indicates an asynchronous twist which is not associated with the formation of a new molecule. If a transition state had indeed been formed we would expect the σC-C forming bond to lie somewhere in between the C-C length (1.54Å) for and Sp³ σ_C-C bond and the sum of the Van der Waal radii (3.14Å) for two carbon atoms. This is indeed the case with the bond length of 2.12 Å for the AM1 and 2.27 Å for the more experimentally accurate DFT method. We also see that there is a difference between the single and double bonds in the fragments indicating that the we have an early transition state where the the transition structure is "reactant-like". The fragment double bonds are ca 1.40 Å which is longer than a Sp₂ C=C alkene bond (1.33 Å) consistent with the fact that this bond is in the process of breaking (i.e. it lengthens). Similarly the C-C single bond on the butadiene fragment is also ca 1.40 Å which is shorter than the standard 1.54 Å for C-C alkane bonds, suggesting a double bond is forming.

HOMO-LUMOs Transition state

Method	HOMO	LUMO
Semi-empirical AM1	HOMO	HOMO
DFT-B3YLP/6-321g*	HOMO	LUMO

Inspection of the a HOMO for the AM1 method indicates that the structure has formed by interaction of the a HOMO of cis-butadiene and a LUMO of ethylene. Likewise inspection of the s LUMO at this level of theory indicates contributions from the s LUMO of cis-butadiene and s HOMO of ethylene. The matching of the symmetry of the HOMO-LUMO fragments showing good overlap indicates the reaction is allowed. Considering the DFT results, although we can match the ethylene fragment part of the HOMO with the s HOMO of ethylene we cannot match the butadiene fragment with the HOMO or LUMO orbitals above; we may attribute this to the different ordering of the orbtials under the DFT method thus highlighting the importance of choice of method.

Diels Alder: cyclohexa-1,3-diene reaction with maleic anhydride

We will now investigate regioselectivity in the reaction of cyclohexa-1,3-diene reaction with maleic anhydride by analysing the transition states and orbital effects. Once again a semi-empirical AM1 method will be used due to its simplicity and effectiveness; in the interest of time as this system is more complex the AM1 method is appropriate. The fragments are first optimised and then computation of the transition states undertaken.

AM1 optimisation - HOMO-LUMO cyclohexadiene/maleic anhydride DOI:10042/to-7318 DOI:10042/to-7319

HOMO cyclohexadiene	LUMO cyclohexadiene	HOMO maleic anhydride	LUMO maleic anhydride

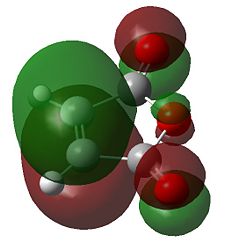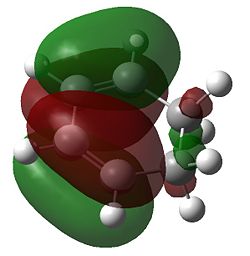
The HOMO and LUMO are respectively a and s with respect to the plane of symmetry down the C-C between the double bonds for cyclohexadiene. They will therefore combine with the a LUMO and s HOMO of maleic anhydride respectively to form a new HOMO and LUMO.

We begin by orientating the two fragments in such a way so as to increase the chances of finding the exo and endo transition states:

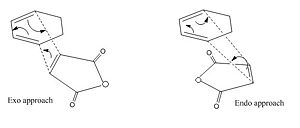
[Note that for the endo structure we require the -CH2CH2- region of the cyclohexadiene to be out-of plane for gaussian to locate the transition state; otherwise we observe strong repulsion of the two fragments]

Following this we optimise to a TS(berny). The results are summarised below:

Exo/Endo transition states

Approach	TS	Animation	Frequency/cm-1
Exo DOI:10042/to-7292	exo ts E = -0.050419 a.u.	Vibration "Z-like" TS	- 812
Endo DOI:10042/to-7290	endo ts E = -0.051505 a.u.	Vibration "U-like" TS	-806

To confirm the exo and endo transition states structures lead to the respective product an IRC was run with force constants calculated at all steps. The energies were -0.150991a.u. and -0.160170 a.u. giving an energy difference of 24.1kJ/mol.

Exo(left) DOI:10042/to-7293 / Endo(right) DOI:10042/to-7294

EXO	ENDO

Going back to the transitions states we observe two imaginary frequencies (one/per structure) indicating the presence of a transition state maximum. The C-C σ to π and π to σ forming bonds are in the region of 1.40 Å which lies in between an Sp₃ single and Sp₂ double bond. This helps verify that we are at a transition state in additon to the two synchronous imaginary frequencies of 812cm_-1 and 806cm_-1. By comparing the absolute electronic energies the endo form is 2.85kJ/mol more stable than the exo form. Why is this ? Initial inspection of the -(C=O)-O-(C=O)- fragment of the maleic anhydride to the (to be) bridging carbon of the cyclohexadiene for both structures gives very similar lengths; for the exo we see 2.94 Å and for the endo we see 2.89 Å. We can present a rather crude steric argument that the (to be) bridging carbons in the cyclohexadiene for the exo are "sp₃ hybridised", have 2 hydrogens, one of which is 2.75 Å away from the oxygen, compared to the planar hydrogen which points away at 3.45 Å for the endo form. However, if we were to go by the arguments presented in part one we would expect a stabilising Van der Waal attraction at the distance of 2.75 Å for the exo form. This suggests that there must be a different reason for the stability of the endo form. We therefore take consideration of the MOs.

HOMO-LUMOs Transition state

	HOMO	LUMO
Exo	HOMO	LUMO
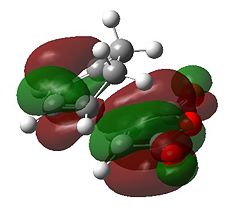Endo	HOMO	LUMO

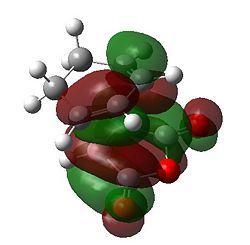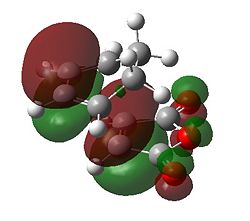
First of all it can be seen that the HOMO of the exo and endo forms has been formed from the a HOMO of cyclohexadiene and the a LUMO of maleic anhydride. This makes intuitive sense as the maleic anhydride acts as the dienophile where the electronegative oxygens lower the energy of the LUMO to enable a good reaction with the HOMO. The LUMO of the transition state appears to be formed from the LUMO for the maleic anhydride and another MO on the cyclohexadiene; this is not important for the discussion as this is unfilled. For both structures there is a nodal plane passing through the ring oxygen and two carbonyl groups. It appears that the antibonding interaction along this plane is identical for both transition states. There must be another reason for the stability of the endo form over the exo.

Secondary Orbital effects

There is much literature concerning secondary orbital effect in the Diels Alder reaction which account for the endo form being the kinetic product. An example of one of the many pieces of work carried out on this is that from Marye Anne Fox et al. who investigate the balance between steric effects and secondary orbital overlaps (SOO). Here they define a SOO as SOO is defined as "the positive overlap of a non active frame in the frontier molecular orbitals of a pericyclic reaction", i.e. an interaction of orbitals not involved in the primary bond forming overlaps. The SOO is not apparent for all Diels Alder reactions and the endo regioselectivity can also be overridden by sterics if for example there is a bulky group which increases the energy of an endo approach. Taking a Frontier Molecular Approach to considering these effects can prove quite effective in predicting the most favourable outcome of the reaction.

Exo/Endo orbital effects

Approach	FMO approach	Calculated HOMO-1
Exo	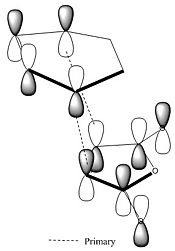exo orbital effects
Endo	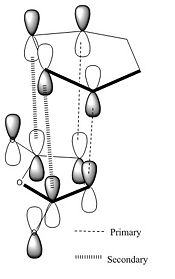endo obital effects

This stabilising secondary orbital overlap is possible for the endo form purely based on the approach it takes. It is apparent if we consider the HOMO-1 orbitals whereby the bottom half of the large lobe on the cyclohexadiene interacts with the antibonding orbitals on the dienophile. For the exo form no secondary orbital effect is observed.

Further Discussion

Had time permitted further work would have been undertaken involving varying the substituents on the reacting fragments to investigate the balance between steric influences and orbital contributions in the Diels-Alder reaction. Fundamentally, what has not been addressed has been the simple question "what affects a Diels-Alder reaction?" - to which there is a rather complex answer! Additional investigation into improving the method and basis sets used to explore the electron correlation effects on the molecules could be undertaken. This will help paint a more accurate picture as say a larger or more appropriate basis set, with additional functions to suit the particular molecule of interest could be tailored. However, within the scope of this experiments time-frame unfortunately this was not possible.

Conclusion

In conclusion, we have seen the effectiveness of computational studies in predicting the energies of various conformers and computing the transition states and reaction paths. Throughout the experiment the importance of a plausible initial geometry has been highlighted when considering the "chair" and "boat" paths. Activation energies have been estimated using two levels of theory and these are in good agreement with experimental data. Various techniques have been explored to compute transition states and compute the structures along the reaction path as well as generation of the MOs. This has proved valuable in predicting the regioselctivity for the Diels-Alder reaction involving cyclohexdiene and maleic anhydride. The task now is to apply the existing theory to more complex systems where perhaps a mix of crude methods such as the semiempiral AM1 and more sophisticated DFT methods can be used to balance the trade-off between time of experiment and accuracy.