Rep:Mod:nathanmarch

The following is a summary of work carried out using ChemBio3D Ultra 12.0, Guassian 09W and GaussView 5.0, Imperial College Chemistry Department - 3rd Year Computational Labs.

Conventions:

• #-ring indicates an n-membered ring
• References are grouped at the end of each module
• Jmol files for certain molecules have been included as clickable buttons that will open the jmol file in a separate window.
• Energies are displayed in Hartree units (E_h), where 1 E_h = 627.509391 kcal mol^-1

Module 1

The Hydrogenation of Cyclopentadiene Dimer

Introduction

Fig. 1.1.1 Dimerization of cyclopentadiene

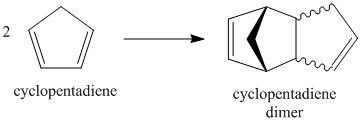
Cyclopentadiene undergoes self-Diels-Alder (Fig 1.1.1) to yield a dimer with two possible configurations: exo or endo (Fig. 1.1.2). Which isomer is favoured over the other is a matter of molecular orbital theory, and is governed by which approach produces the best overlap between the orbitals of the diene and the dienophile - this is largely a kinetic concern. Better overlap in the transition state will lower the activation energy and increase the rate at which the particular isomer is formed. The HOMO of the dienophile interacts more favourably with the LUMO of the diene if in the endo conformation and, regardless of product stability, the route with the lowest activation energy will predominate. Thus, in general, Diels-Alder reactions tend to favour the endo product.

Fig. 1.1.2 Endo and exo approaches

Fig. 1.1.3 Cyclopentadiene HOMO (left) and LUMO (right)

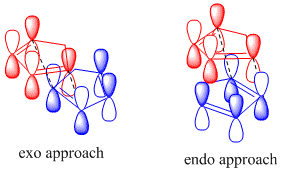
A molecular simulator like ChemBio3D can optimise the geometry of the different isomers and provide thermodynamic information about each - an appreciation of the kinetics depends on being able to simulate the transition state, which is not possible via molecular mechanics modelling. Simulated under identical conditions, the energies of the isomers can be directly compared and an appreciation of the thermodynamics can indicate the most energetically favourable configuration.

The dimer itself still contains unsaturated carbon-carbon bonds: these can be hydrogenated (e.g. via Pd/C), with the possibility that the resulting change in geometry will lower the overall energy. The C=C bonds will henceforth be labelled as being either on the 5- or the 6-ring - the 6-ring bond being the only such bond on a 6-membered ring in the dimer, despite also being part of a 5-ring if the bridge is taken into account.

Analysis

Table 1.1.1 - ChemBio3D optimization data
no dipole-dipole for 5 in output data
Parameter	Energy / 10-3Eh
Molecule:	1	2	3	4	A
Stretch	2.059	1.985	2.037	1.753	1.739
Bend	32.807	33.243	31.638	23.126	20.375
Stretch-bend	-1.341	-1.326	-1.329	-0.873	-0.751
Torsion	12.225	15.145	17.237	19.931	27.324
Non-1,4 VDW	-2.288	-2.404	-1.955	-1.675	-2.226
1,4 VDW	6.744	6.854	8.988	7.182	9.769
Dipole-dipole	0.602	0.709	0.258	0.224
Total Energy	50.809	54.207	56.874	49.669	56.229

Fig 1.1.3 Studied molecules

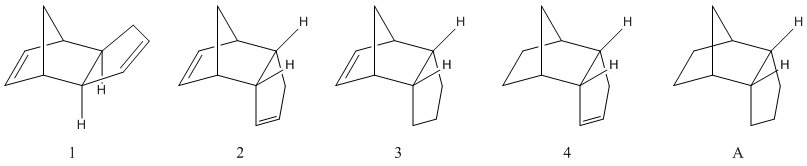
The endo dimer, in spite of the experimental preference, is thermodynamically disfavoured, with the major factor being the torsional strain brought about by the steric interaction between the bridge and the 5-ring (Tab. 1.1.1). The exo dimer is more stable than the endo dimer: the reaction between two cyclopentadiene molecules is kinetically controlled.

Hydrogenating on the 5-ring is a thermodynamically disfavoured process (raising the energy by a small, but not ignorable amount). On the other hand hydrogenation of the 6-ring carbon-carbon double bond reduces the energy by an appreciable amount, with one major reduction in the bend energy outweighing a sizeable increase in torsional stress. When hydrogenating the cyclopentadiene dimer it is therefore 3 that is the major product, if singular hydrogenation is the aim. Interestingly, hydrogenation of both positions yields a molecule (A) that is only slightly more stable than 3, despite the large stabilization achieved when moving from 2 to 4 (this squares with the extended periods required to produce the tetrahydro species).

Comparing the individual energy components for 3 and 4 shows that the stretching, bending and 1,4-Van der Waals energies are lower in the endo dimer (mildly, sizeably and reasonably respectively), while the torsional energy, as noted before, is much larger and the non-1,4-Van der Waals energy is marginally larger. The two significant contributions, bending and torsion, can be explained thus: hydrogenating the 5-ring double bond forces an eclispsed conformation between the hydrogens on the 5-ring, creating steric strain; hydrogenation on the 6-ring does not produce such a conformation as methyne hydrogens at the bridging point are gauche to the sp³ hydrogens on the 6-ring. Other energy differences are small but cumulatively important. Linking the specifics of the conformations with the relative energies is difficult when they are so small and distributed around each structure.

Stereochemistry of Nucleophilic Additions to a Pyridinium Ring (NAD⁺ Analogue)

Introduction

Fig. 1.2.1 Stereoselective methylation of prolinol derivative

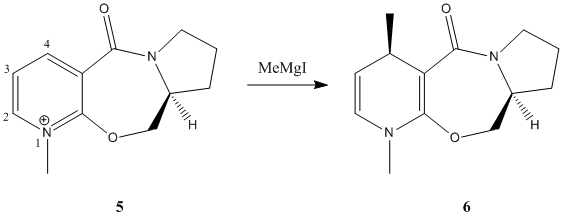
Pyridinium species (speices containing a cationic, protonated/alkylated pyridine ring) can be alkylated on the 4 position of the pryidinium ring by alkylating agents such as Grignards and organolithium reagents. 5 is such a species, however there is a degree of stereoselectivity seen when alkylating that must be accounted for in the production of 6. There is only one other stereocentre in 6, this has a hydrogen that is anti to the methyl on the other stereocentre.

Fig. 1.2.2 Stereoselective addition of aniline to prolinol derivative

Selectivities for this reaction with MeMgBr (and iodine as a counter-ion, 2 hr, -20°C) are about 19:1 (methyl-H trans:methyl-H cis). Bulkier Grignards favour higher selectivites, while organolithium reagents are almost regio- and stereorandom - this method is sufficiently selective in some cases to allow for direct crystallization of the enantiomer.

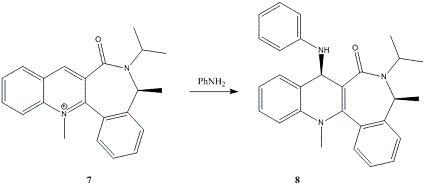
7 is another pyridiniuim species, that displays similar enantioselectivity when reacted with aniline.

Conformational analysis, via molecular mechanics modelling, should provide sufficiently enlightenment as to the 3D structure of 5 and 7 that a reasonable hypothesis as to the mechanism of each reaction can be reached. It is the conformation of the carbonyl relative to the plane of the ring that is likely to be of most interest as two possible effects could become important: a) the chelation of the nucleophile (or some portion of the nucleophile) could draw the nucleophile to the same side of the ring that the carbonyl occupies, or b) steric repulsion between the carbonyl and the attacking group favours addition to the other face of the pyridinium ring. For further discussion the 'upper-side' refers to the side anti to the chiral centre hydrogen, while the 'lower-side' refers to the side syn to the chiral centre hydrogen.

Results and Analysis

The optimized geometry of 5, using ChemBio3D (RMS Gradient = 0.100), has the carbonyl tilted slightly upward (anti to the chiral centre hydrogen). A molecular dynamics simulation, up to 2500 iterations, 300K, saw the carbonyl deviate back and forth but rarely passing below the ring and never by an appreciable amount. Simulating a number of starting configurations, and optimizing each under the same conditions, produced low energy conformations with the carbonyl above the plane of the pyridinium ring (p-ring) or high energy conformations with the carbonyl below (the one case where this did happen to an extreme degree had such exceptional geometry that it can be, for all intents and purposes, disregarded.

Table 1.2.1 - conformations of 5 before and after MM2 optimization
Configuration	1	2	3	4
Pre-optimization	automatic geometry produced when inputing structure	carbonyl placed far below the p-ring	carbonyl placed far below the ring with prolinol p-ring raised	structure widely dispersed, carbonyl placed below the p-ring
Post-optimization	carbonyl about 10° off the plane of the p-ring, anti-H	carbonyl about 10° off the plane of the p-ring, but highly strained prolinol ring	carbonyl about 90° below the p-ring, but highly excentric geometry	carbonyl about 10° below the p-ring, p-ring distorted
Energy / 10-3Eh	70.297	306.418	222.568	223.428

Fig. 1.2.3 Chelation mechanism for Grignard methylation of 5

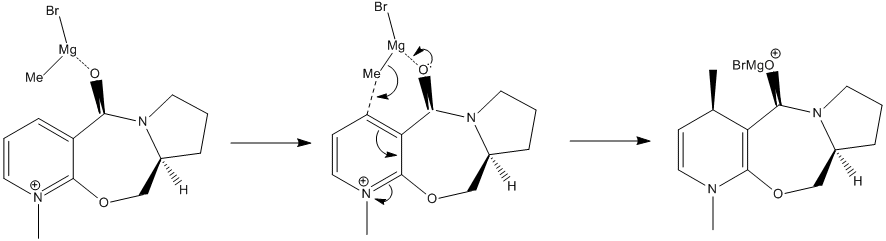
The only low-energy conformation has the carbonyl anti to the chiral centre hydrogen, while any structures where the carbonyl is below the ring are either of too high-energy to be of significance or have such exceptional geometries that they bear no resemblance to their real-world counterparts.It can be inferred from this that the mechanism of nucleophilic attack follows the first of those theorized above: the carbonyl is chelated by magnesium causing the methyl to be transferred to the upper face of the p-ring. This behaviour is to be expected with the electron-rich/electron poor (Lewis base/Lewis acid) pair.

Molecule 7, on the other hand, displays the other form of behaviour, the aniline attacking anti to the carbonyl:

Table 1.2.2 - conformations of 7 before and after MM2 optimization
Configuration	1	2	3
Pre-optimization	automatic geometry produced when inputing structure	carbonyl placed above the ring (syn to methyl), prolinol portion moved down	structure widely dispersed, carbonyl placed above the p-ring
Post-optimization	carbonyl about 10° below the plane of p-ring, anti to chiral centre methyl	carbonyl about 10° below the plane of p-ring	carbonyl about 10° below the plane of p-ring, strange orientation of benzyl hydrogen

Fig. 1.2.4 Steric mechanism for the anilination of 7

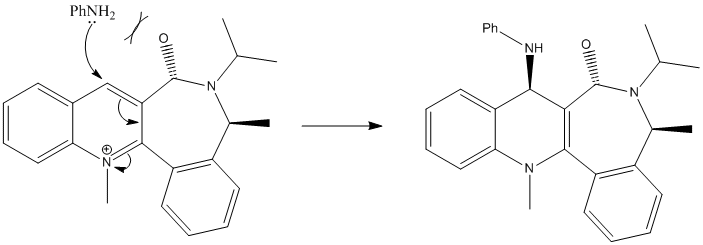
All input configurations optimized to yield the carbonyl syn to the chiral centre methyl group, though some structures did display some 'structural eccentricities' (these are likely a product of the extreme structures that were input). From the evidence one should conclude that the enantioselectivity of the anilination of 7 is a result of the second mechanism proposed in the introduction, that of steric repulsion between the carbonyl and the nucleophile leading to attack on the face anti to that of the carbonyl group. One would not expect the same sort of chelation behaviour between two Lewis bases.

These models could be improved by studying the transition states for the molecules, or calculating the molecular orbitals: if one were to analyse the shapes and characters of the HOMOs and LUMOs of 5 and 7, particularly about the carbonyl and reactive centre, one could have a more definitive indication of the degree to which attack on one face is favoured over the other. Studying the transition states, if sufficiently accurate, will give specific energies for each reaction and a good estimate of the kinetics. The stoichiometric ratios would therefore be determinable.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

Introduction

Fig. 1.3.1. Atropisomers of taxol total-synthesis intermediate

Atropisomerism arises in systems of general free rotation that are nevertheless contrained in one of a number of stable configurations that do not necessarily interchange at room temperature. Such stable conformers need not be equally stable, but need only a sufficiently large kinetic barrier to interconversion. Geometric reasons for such isomers include rings (being unsaturated or partially saturated) and 2,2'-6,6'-diphenyl species.

One of the synthetic intermediates on the road to paclitaxel (Taxol®) has two atropisomers: one has the carbonyl pointing 'upward' while the other has the carbonyl pointing 'downward' (Fig. 1.3.1); both are stable. One problem that arises from this is the difficulty is achieving highly selective addition to the carbonyl. The geometry of the neighbouring groups highly favour one Bergi-Dunitz trajectory for each atropisomer, but the trajectory is one the opposite face for each atropisomer. To achieve a fuller understanding of the outcome of an addition to the carbonyl group one can model each atropisomer, minimise and determine the energy, and therefore infer which atropisomer is the dominant form, designing the synthesis accordingly. One of the reasons behind the rigidity of this intermediate is the presense of a bridgehead alkene that provides a sufficiently rigid structure for the remainder of the molecule to deform around.

Results and Analysis

Conformations

Table 1.4.1 - Energies of successive conformations
Molecule	Conformation	Preparation	Post-Opt Energy / 10-3Eh	Notes
9	a	Carbonyl on 10a moved syn to bridge	86.207	6-ring in twist-boat conformation
	b	6-ring manipulated into chair conformation	86.207	6-ring returned to twist-boat conformation
	c	6-ring manipulated into other chair conformation	77.887	Conformation was stable
10	a	Structure drawn and optimized without manual alteration	76.772	Lower energy than 9a-c, 6-ring in twist-boat conformation
	b	6-ring manipulated into chair conformation	76.772	6-ring returned to twist-boat conformation
	c	6-ring manipulated into other chair conformation	70.557	Conformation was stable

Modelling the atropisomers started with inputing the clean structure into ChemBio3D. This structure was not modified prior to running an MM2 (minimise energy) calculation, and the product of the calculation was molecule 10 - already a good indication that it is the most stable conformer. Manually shifting the carbonyl to be above the ring, followed by a further MM2 optimization, yielded 9. The geometries of both 9 and 10 were altered to yield the lowest possible energy conformers; this was done in manual steps, by moving atoms around to visually better positions, followed by an MM2 energy minimisation (default settings) with a low RMS gradient (0.001) to finish with, when no further large reductions could be found (10c and 9c).

From the simulations, it seems that the 6-ring can be in either of the twist-boat or chair conformations, however only the chair conformation where the carbon β to the carbonyl is anti to the carbonyl - if syn, optimization results in a reversion to the twist-boat conformation. This is due to the steric interactions between the carbonyl and the hydrogens on the β-carbon destabilizing that chair conformation.

Alkene Stability

The two atropisomers are both examples of hyperstable alkenes. Hyperstable alkenes are labelled thus due to their unusual reluctance to undergo hydrogenation. A hyperstable alkene is thermodynamically more stable than it's hydrogenated derivative. This behaviour, contrary to conventional bond-enthalpy-informed wisdom, is due to the unique structures under examination; the strain present in the alkene is worsened by hydrogenation: the pressure exerted by the transformation of sp² carbons in sp³ carbons on the conformationally restricted system destabilizes the whole molecule, by a degree greater than bond formation can stabilize.

9 and 10 were 'hydrogenated' and had their energy minimised - both 9 and 10 were input to see how each atropisomer would respond however the response of ChemBio3D, which redrew each structure as it was changed, made any such efforts pointless. The various conformations were manipulated until the following, lowest-energy conformation, was produced, having an energy of 90.278 x 10^-3E_h. A thermodynamically disfavoured product will form in high yield only because the reaction is irreversible, but the reaction will always be slow unless higher temperatures are used.

Regioselective Addition of Dichlorocarbene

Introduction

Fig. 1.4.1 - Chloro-diene

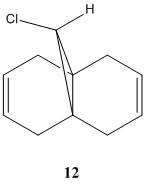
Certain reactions defy the conventional means for predicting the major products. Sterics, simple stereoelectronics, thermodynamics etc. are sometimes insufficient, making molecular mechanics of little use. Analyzing the molecular orbitals, however, can be eminently useful as this provides regiospecific information about the viability of electron donation or acceptance.

Dichlorocarbene, a potent electrophile, reacts with alkenes to yield 1,1-dichlorocyclopropane species. There are three adducts in the case of diene 12, the diadduct and the two regioisomers of the monoadduct. The molecular orbital approach has a number of different strengths of approach: the PM3 method yields sensible results, while more recents methods include RM1 and PM6. The difference between the methods is unimportant here, it is simply the method that yields the most realistic results that should be used; certain methods are not amenable to certain molecules, so it is important to appreciate the limits of any one method. PM6 is used here because it is the later version of a method that has already been shown to yield sound results.

Results and Analysis

Part 1 - Orbitals of an Assymmetric Diene

12 was modelled using the PM6 method via the ChemBio3D MOPAC interface. The HOMO-1, HOMO, LUMO, LUMO+1 and LUMO+2 were computed (among others), with the specific focus of interest in each being the presense of electron density on the carbon-carbon double bonds.

File:H Fig 1.4.2 - HOMO-1 of 12 '

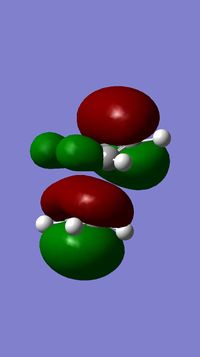Fig. 1.4.3 - HOMO of 12 majority of electron density on the syn double bond

Fig. 1.4.4 - LUMO of 12 majority of electron density on the anti double bond - highlights electron deficiency of that bond

Fig. 1.4.5 - LUMO+1 of 12

Fig. 1.4.6 - LUMO+2 of 12

Fig. 1.4.7 - LUMO of dichlorocarbene

The alkene most favoured in 12 in the HOMO is the endo alkene, having hugely more electron density associated with it. It is the HOMO that defines the alkenes' electrophilic activity, as it is electrons from the HOMO that will donate into the singlet carbene's p-orbital-based LUMO.

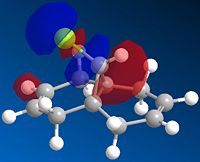
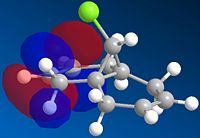
The symmetry of the CCl₂ LUMO matches the symmetry of the alkene HOMO if it approaches along the plane of the ring, perpendicular to the double bond. The anti double bond is very electron-poor (Fig. 1.4.3) compared with that syn to the chlorine - it will be far less reactive with the carbene, and will be the minor monoadduct in the reaction. The two approach trajectories for the carbene lack discrimating factors like sterics so the relative success of each mono-addition reaction can be understood solely from an MO perspective. Quantitative analysis would require transition state modelling but a qualitative approach like MO theory is sufficient in this case.

Part 2 - Vibrations of 12 and its Dihydro Derivative

• Vibrational analysis in this section was done with the aid of files provided by Georgina Gregory, in order to save computing time.

Fig. 1.4.8 - Anti dihydro derivative of 12

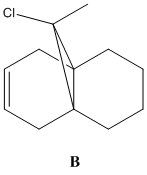
12 has a plane of symmetry, a single σ_h that is its only valid, non-identity symmetry operation - it is part of the C_s symmetry group. In terms of calculating the properties of 12 this is a great benefit as a program need only model half of the model to model the whole; it applies what has been determined on one half of the molecule, by symmetry, to the rest. The dihydro derivative of 12 has a buckled 6-ring (twist-chair conformation - Fig. 1.4.8)) that invalidates the plane of symmetry present in 12, and leaves B with C₁ symmetry.

Fig. 1.4.9 - π-σ* donation in 12 (left) and equivalent orbitals in B (right)

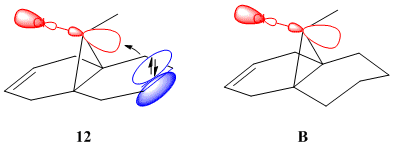
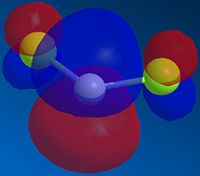
One of the novel effects that can be seen in this system is the increase in the vibrational energy of the chlorine-carbon bond as a result of hydrogenating the anti alkene bond. The computed vibrations of 12 consisted of the usual symmetrical and assymmetrical stretches, scissoring, rocking, wagging and twisting one would expect and need not be shown. What is important is the stretch of the C-Cl bond: this bond has a frequency of 770.92 cm^-1 in 12 and 774.96 cm^-1 in B. What can be inferred from the increase in energy of the C-Cl bond upon hydrogenation is that the bond is weaker in 12 than in B: as can be seen from Fig. 1.4.9, the theorized explanation of this behaviour is that the π_C=C,anti orbital donates electron density into the σ*_C-Cl orbital, weakening the C-Cl bond. In B the lack or an orbital of the correct symmetry with similar electron density precludes any such effect.

The C=C bond vibrations for 12 are 1737.13 cm^-1 for the anti alkene and 1757.37 cm^-1 for the syn alkene; this is confirmation of the nucleophilicity assigned in Part 1: the anti alkene bond has a weaker (lower energy) bond stretch that that of the syn alkene, and is therefore less electron-rich i.e. less nucleophilic.

B's alkene has a strech energy of 1758.06 cm^-1, basically the same as prior to hydrogenation. What effect the conversion of the anti carbons from sp² to sp³ has on the syn alkene is likely not a result of directly traceable electronic effects but has more to do with the altered geometry happening to distort the structure to the point where it is ever-so-slightly harder to distort the syn double bond.

Fig. 1.4.10 - Predicted IR spectrum of 12

Fig. 1.4.11 - Predicted IR spectrum of B

Mini-project: Alkene Selectivity in the Production of Regio-restricted Enol Silyl Ethers

Introduction

The purpose of this project was to explore how to distinguish between two isomers that are the outcome of a single reaction via computational methods, as an excercise to see how computational methods can be useful in informing the deconvolution of spectral data and providing insight into which methods of analysis might be useful.

The criteria for selection of a sample reaction for analysis were as follows:

• Produces two, and only two, isomers, whether regio-, stereo- or diasteroisomers: these will then be analyzed via computational methods to determine how, practically, one could distinguish between them.
• The starting materials and products should have literature-recorded ¹³C NMR data/spectra that can be used for comparisons with the computed spectra.
  • To that end, the reaction should be sufficiently variable in its output as to allow both isomers to be produced under different conditions such that spectral analysis is possible.

Fig 1.5.1 - Silyl ether derivatives of enolates of propiophenone

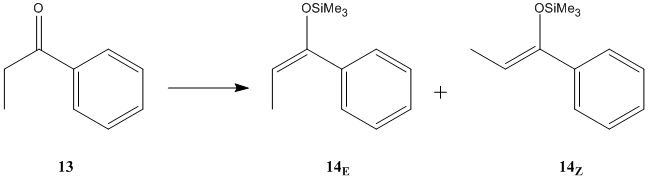
The reaction chosen is the enolization of propiophenone:

• An enolizable species that displays regioselectivity, having one hydrogen-baring substituent α to the carbonyl
• A small molecule, such that computing times will be minimized
• A reaction for which the products (the silyl ether derivatives to be precise) have literature ¹³C NMR data
• A reaction for which each isomer can be selected for:
  • Deprotonation of propiophenone with LDA, followed by reaction with trimethylsilyl chloride leads exclusively to the Z-alkene
  • Using lithium bis(trimethylsilyl)amide as a base yields a mixture of the E- and Z-alkenes in a ratio of 30:70 - HPLC can then be used to isolate the E-alkene

Selectivity in the formation of enolates has two problems, that of regioselectivity (usually expressed through kinetic or thermodynamic products, depending on proton acidity and the alkene substitution) and diastereoselectivity (whether the resulting alkene is E or Z). Using propiophenone is ideal due to the lack of α-hydrogens on the phenyl group, making the kinetic vs. thermodynamic discussion not pertinent. The silyl ether derivatives were chosen over the anionic enolates as the presense of formal changes would have made the analysis more difficult - not to mention that NMR data for the enolates would be with counter-ions, that could not be easily replicated in computational simulation, and that would affect the chemical shifts.

The most means most likely to distinguish between the two isomers is ¹³C NMR, specifically the NMR of the alkene methyl substituent, that in one conformation will be trans to a silyl ether and in the other will be trans to a phenyl group. ¹H NMR is another method that could yield good results but prediction of ¹H chemical shifts is less reliable than for ¹³C. Optical rotations will not be productive, ³J_H-H couplings will be unhelpful as they are not likely to change significantly (had the phenyl been, instead, a hydrogen ³J_H-H couplings would be an ideal method as trans- and cis-alkene ³J_H-H couplings vary by a number of Hz.

¹³C NMR

Fig. 1.5.2 - Nuclei for ¹³C NMR

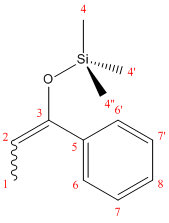
NMR data was calculated using the DFT-MPW1PW91 optimization,and is summarizied in Tab. 1.5.1.

Table 1.5.1 - NMR Data for 14E and 14Z
C#	14E (lit.)	14E (pred.)	14Z (lit.)	14Z (pred.)
1	13.0	181.3	11.6	182.8
2	104.8	88.7	105.2	89.3
3	149.6	48.8	149.9	47.7
4	0.1	195.9,195.9,196.9	0.5	194.0,194.3,197.4
5	137.5	61.6	139.2	58.6
6	127.7	71.5,72.1	127.3	74.5,74.6
7	128.3	71.9,73.1	128.0	72.0,72.2
8	127.4	72.6	125.2	72.9

The NMR predictions do not match the literature at all, though they are self-consistent. This would seem to indicate that a mistake was made in the input file - the data is shown to illustrate that the predicted NMRs for the two isomers are different. The largest differerences between the two isomers seen in the literature is with C5 (Δδ = 1.7 ppm), and C1 (Δδ = 1.4 ppm), but given the inaccuracies with the predicted data any analysis of the relative chemical shifts will not be productive for showing how one isomer could be distinguished from the other. What the prediction was supposed to do was corroborate the literature data, such that confident future analysis of other systems would allow non-literature-supported analysis to be done; too bad.

Fig. 1.5.3 - Predicted ¹³C NMR spectrum of 14_E

Fig. 1.5.4 - Predicted ¹³C NMR spectrum of 14_Z

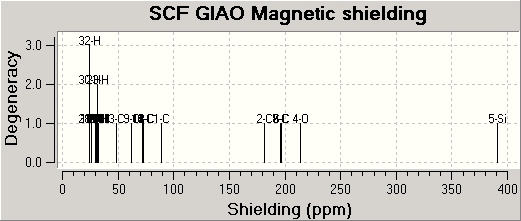
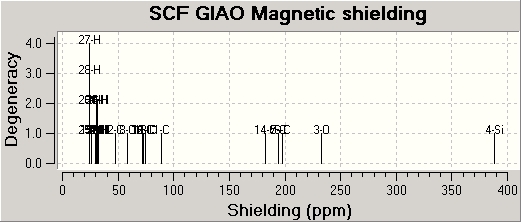
MO Calculations

The starting material was submitted, post-optimization, for MO calculations but failed to produce results. In it's place, ChemBio3D calculations of the molecular surface will have to suffice.

The reactant can be drawn in the form that it must take prior to forming the enolate, manual manipulation was required for this step but efforts were made to keep the bond lengths as true to life as possible.

Fig. 1.5.3 - LUMO of pre-E-alkene configuration of 13

Both structures were then subjected to a MOPAC/PM6 Molecular Surface calculation to see how much electron density resided on the antiperiplanar hydrogen (in the case of the Z-alkene precursor) or synperiplanar hydrogen (in the case of the E-alkene precursor). What was seen from that investigation was that the Z-alkene, the major product in both syntheses introduced in the introduction, had the largest orbital presense around the hydrogen that would need to be removed by base to form the enolate. The LUMO is examined because the reaction will proceed via the σ*_C-H orbital of the anti/synperiplanar hydrogen.

Fig. 1.5.4 - LUMO of pre-Z-alkene configuration of 13

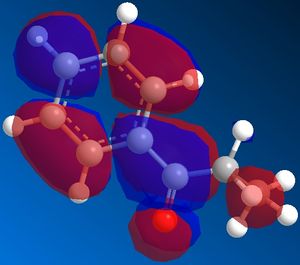
Conclusion

The molecule chosen displayed all the attributes required by the specification, with the particular benefit being its size, allowing DFT-MPW1PW91 geometry optimizations to take approximately one-and-a-half hours. Looking at the NMR data, it would have been better to choose a more conformationally resticted molecule/reaction, that is more amenable to computational methods. The choice of E-/Z-alkene isomerism would have been better had hydrogens been present on both sides of the alkene.

---