Rep:Mod:ka1510
Module 3
Introduction
Modelling transition states using computational methods is important in developing a deeper understanding of the mechanism of a reaction and in identifying its properties (e.g. rate of reaction).
The use of compuational programmes such as Gaussview 5.0 allows you to model the potential energy surface(PES) of a molecule by calculating the total energies and optimal structures of molecules involved in a chemical reaction using different calculaion types. The data obtained from the optimimal structures can be used to carry out further calculations involving the molecule such as calculating the potential gradient and frequency analysis at a certain point on the potential energy surface(PES) of the molecule.
This project involves analysing and carrying out calculations on the transition state structure for two key organic reactions. The structures will be characterised using GaussView 5.0. The two organic reactions which will be analysed in the following project will be:
1) The Cope Rearrangement
2) The Diels-Alder Reaction
The Gaussian programme works by using quantum mechanics to form a Born-Oppenheimer potential energy surface(PES) to represent the transition state structures by plotting the relative energies of each structure against the reaction coordinate. Gaussian defines the reaction coordinate as the path linking the minima optimum molecular structures with the stable intermediates and transition states in a reaction.
The Born-Oppenhemier potential energy surface formed by Gaussian uses some degree of approximation especially in the case of large molecule due to the fact that larger molecules contain too many degrees of freedom for a fully discrete surface. This potential energy surface is then used to characterise the structures involved in the reaction as it progresses.
Frequency analysis of each of the optimal transition state structures should show one large negative frequency. This negative frequency informs you that the structure is a maxima with respect to one particular direction on the potential energy surface.
Potential Energy Surface Diagram
Computational Analysis of Cope Rearrangement of 1,5-hexadiene
Introduction
The Cope rearrangement was discovered in 1940 by Arthur Cope. The rearrangement involves a 1,5-diene molecule undergoing a heat driven 3,3-sigmatropic rearrangement forming a more energetically stable equivalent regioisomer.
The rearrangement reaction below shows that both the reactants and the products are isoenergetic. This therefore suggests that the reaction rate and hence the equilibrium constants for both the forward and reverse reactions are the same. However, if substituents were added to various carbons on the reactant, the resulting products would be differenet in terms of their thermodynamic stability depending on which carbon the substituent lies. The thermodynamic stability of the product will determine which direction the equilibrium shifts.
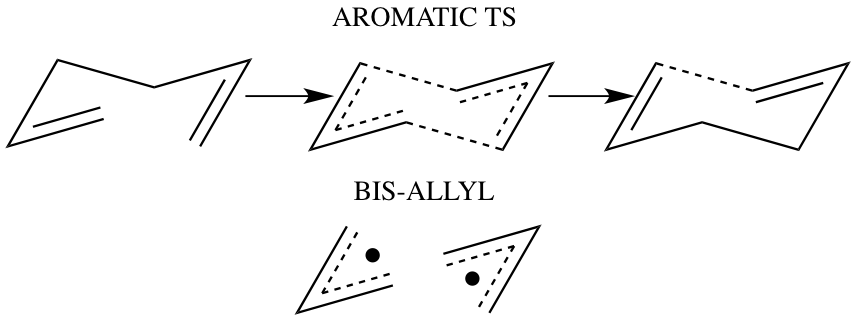
Cope Rearrangement
The rearrangement can proceed via either a chair or boat transition state by a concerted mechanism which occurs without the formation of an intermediate with the bonds formed and broken simultaneously., with the boat orientation transition state reported to have the higher energy:
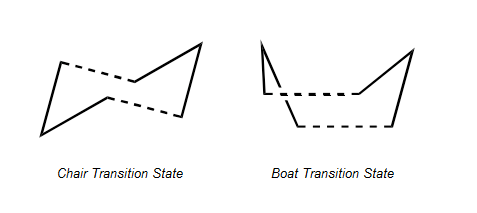
Chair and Boat Orientations
In this part of the project optimsiation calculations are going to be carried out on various low energy transition state structures and their geometries in order to discover the actual mechanism of the Cope Rearrangement.
Optimization and Analysis of 1,5 Hexadiene
"Anti-periplanar" 1,5-hexadiene molecule
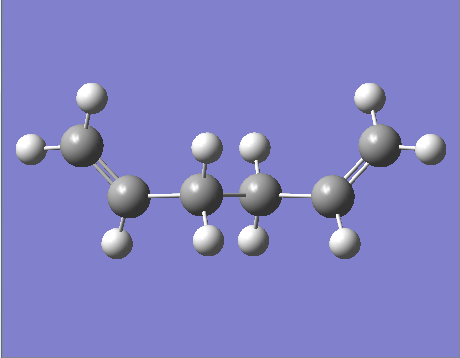
Figure 1. A Gaussview Image of an optimized "anti-periplanar" C6H10 molecule
A 1,5-hexadiene molecule with "anti-periplanar" linkage was created in GaussView and then optimised using a Hartree Fock 3-21G minimal level basis set on the HPC server.
Results from the Log. File1C6H10 and gaussview summary provided below:
D Space: http://hdl.handle.net/10042/24053
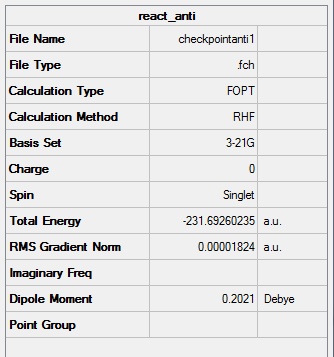
Figure 2. Gaussview Summary optimized "anti-periplanar" 1,5-hexadiene - 3-21G- HF
The following information was obtained following the optimization and symmetrizing of the "anti-periplanar" 1,5-hexadiene molcule:
Point Group: C2
Energy: -231.69260235 a.u
"Gauche" 1,5-hexadiene molecule
Figure 3. A Gaussview Image of an optimized "gauche" 1,5-hexadiene molecule
A 1,5-hexadiene molecule with "gauche" linkage was created in GaussView and then optimised using a Hartree Fock 3-21G minimal level basis set on the HPC server.
Results from the Log. File2C6H10 and gaussview summary provided below:
D Space: http://hdl.handle.net/10042/24059
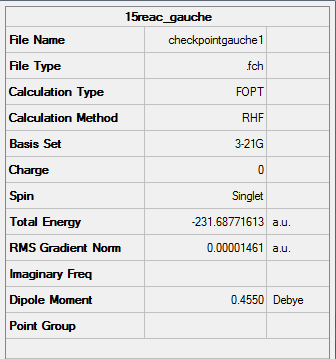
Figure 4. Gaussview Summary of an optimized "gauche" 1,5-hexadiene - 3-21G- HF
The following information was obtained following the optimization and symmetrizing of the "gauche" 1,5-hexadiene molecule:
Point Group: C2
Energy: -231.68771613 a.u
Comparison between a "gauche" 1,5-hexadiene conformation and a "anti-periplanar" 1,5-hexadiene conformation
It appears from the optimization data that the "gauche" conformer was found to have a slightly higher total energy than that of thw "anti-periplanar" conformer. This can be explained by the steric clash of the two C=C groups which can be seen in Figure. 2 above. These two C=C groups are much closer to each other in the "gauche" conformer in comparison to the "anti-periplanr" conformer and this results in the energy of the conformer being higher.
Lowest Energy Conformer
| Conformer | Structure | Point Group | Energy - 3-21G(HF)/a.u | Relative Energy/a.u |
|---|---|---|---|---|
| Gauche 1 |  |
C2 | -231.68772 | 3.10 |
| Gauche 2 |  |
C2 | -231.69167 | 0.62 |
| Gauche 3 |  |
C1 | -231.69266 | 0.00 |
| Gauche 4 |  |
C2 | -231.69153 | 0.71 |
| Gauche 5 |  |
C1 | -231.68962 | 1.91 |
| Gauche 6 |  |
C1 | -231.68916 | 2.20 |
| Anti 1 |  |
C2 | -231.69260 | 0.04 |
| Anti 2 |  |
Ci | -231.69254 | 0.08 |
| Anti 3 |  |
C2h | -231.68907 | 2.25 |
| Anti 4 |  |
C1 | -231.69097 | 1.06 |
Figure 5. Table of Low-Energy conformers of 1,5-hexadiene1
Ci "anti-periplanar" Conformation of 1,5-hexadiene
Figure 6. A Gaussview Image of an "anti-periplanar" Ci symmetry 1,5-hexadiene molecule
Ci symmetry "anti-periplanar" Conformation of 1,5-hexadiene Optimization (3-21G)
A Ci symmetry 1,5-hexadiene conformer with "anti-periplanar" linkage was created in GaussView and then optimised using a Hartree Fock 3-21G minimal level basis set on the HPC server.
Results from the Log. File3C6H10 and gaussview summary provided below:
D Space: http: http://hdl.handle.net/10042/24067
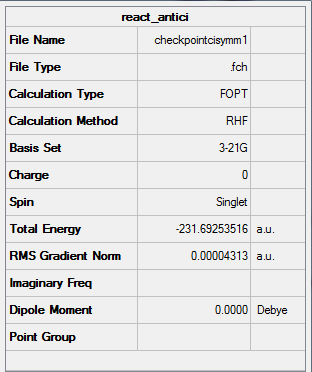
Figure 7. Gaussview Summary optimized "anti-periplanar" Ci symmetry 1,5-hexadiene - 3-21G - HF
The following information was obtained following the optimization (3-21G,Hartree Fock) and symmetrizing of the Ci symmetry "anti-periplanar" 1,5-hexadiene molecule:
Point Group: Ci
Energy: -231.69253516 a.u
C=C Bond Length: 1.32 Å (3.s.f)
C-C Bond Length: 1.51 Å (3.s.f)
C-H Bond Length: 1.07 Å (3.s.f)
Ci symmetry "anti-periplanar" Conformation of 1,5-hexadiene Optimization (6-31G)
A Ci symmetry 1,5-hexadiene conformer with "gauche" linkage was created in GaussView and then optimised using a DFT, 6-31G higher level basis set on the HPC server.
Results from the Log. File4C6H10 and gaussview summary provided below:
D Space: http: http://hdl.handle.net/10042/24083
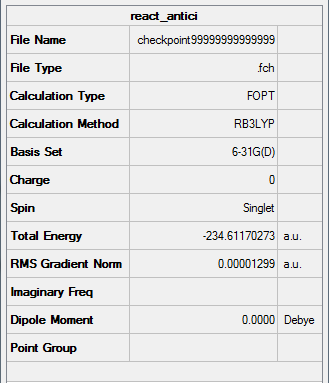
Figure 8. Gaussview Summary of an optimized "anti-periplanar" Ci symmetry 1,5-hexadiene - 6-31G - DFT
The following information was obtained following the optimization (6-31G,DFT) and symmetrizing of the Ci symmetry "anti-periplanar" 1,5-hexadiene molecule:
Point Group: Ci
Energy: -234.61170273 a.u
C=C Bond Length: 1.32 Å (3.s.f)
C-C Bond Length: 1.50 Å (3.s.f)
C-H Bond Length: 1.08 Å (3.s.f)
Ci symmetry "anti-periplanar" Conformation of 1,5-hexadiene Frequency Analysis
A frequency analysis was then carried out using the previously 6-31G(DFT) optimized Ci symmetry "anti-periplanar" conformation of 1,5-hexadiene. The frequency analysis enables you to find the minimum structure of the molecule on a potential energy surface.
The frequency calculation also produces the frequencies of vibration in an infrared spectrum which can be compared to literature values. This allows you to draw a conclusion as well as analyse the outcome of your frequencies with respect to the molecule.
In this particular case, the optimized Ci conformation underwent a frequency analysis claculation to confirm the presence of a minimum critical point on it's potential energy surface. This is proved by the positive vibrational frequency values which are indicated in the logfile of the frequency analysis.
Results from the Log. File1C6H10freq and gaussview summary provided below:
D Space: http://hdl.handle.net/10042/24085
Figure 9. Frequency Analysis for Ci Symmetry "anti-periplanar" Conformation of 1,5-hexadiene
The low frequency values have been extracted from the corresponding output file and show that the frequency calculation is complete:
Low frequencies --- -18.8356 -11.7240 -0.0006 -0.0003 -0.0002 1.7246 Low frequencies --- 72.7097 80.1378 120.0090
Zero-point correction= 0.142491 (Hartree/Particle) Thermal correction to Energy= 0.149847 Thermal correction to Enthalpy= 0.150791 Thermal correction to Gibbs Free Energy= 0.110881 Sum of electronic and zero-point Energies= -234.469212 Sum of electronic and thermal Energies= -234.461856 Sum of electronic and thermal Enthalpies= -234.460912 Sum of electronic and thermal Free Energies= -234.500822
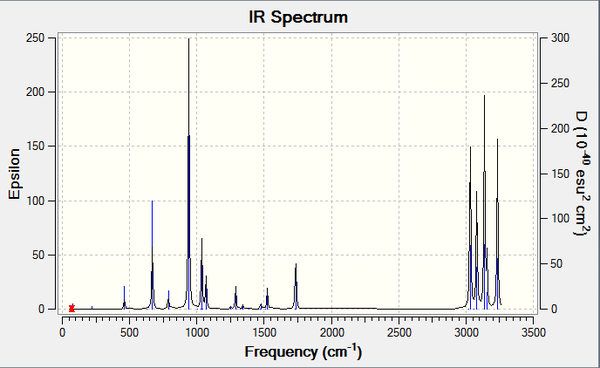
Figure 10. Infrared Spectrum of Vibrating Ci Symmetry "anti-periplanar" Conformation of 1,5-hexadiene
Optimizing the "Chair" and "Boat" Transition Structures
Chair Transition State
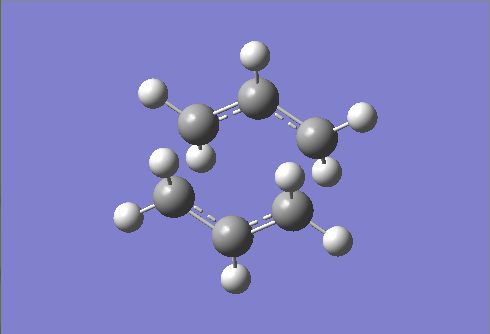
Figure 11. A Gaussview Image of a Transition State Optimization of Two Allyl Fragments with a Chair Orientation
Hessian Method
Figure 12. A Gaussview Movie Showing the Vibrations of an Optimized Chair Orientation (Hessian Method Method) - Opt+Freq
Two allyl fragments (CH2CHCH2) were drawn initially on Gaussview 5.0 and then the transition state was optimized using a 3-21G - (Hatree Fock) minimal basis set. Transition state optimizations are more difficult than minimizations because the calculation needs to know where the negative direction of curvature (i.e. the reaction coordinate) is.
For this reason the two molecules were placed in an orientation similar to that of a chair transition state which has an approximate distance of ~2.2Å between the terminal carbons of the two fragment molecules.
These two fragments were then optimized to a chair transition state using the Hessian Method and the force constants were recorded once the optimization had been complete.
Results from the Log. File1Chair and gaussview summary provided below:
D Space: http://hdl.handle.net/10042/24091
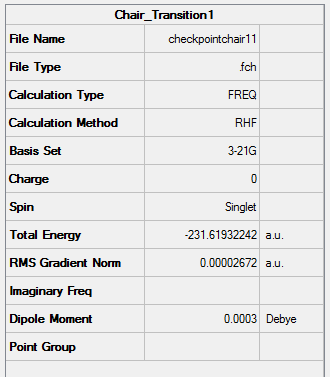
Figure 13. Gaussview Summary of Optimized Chair Orientation(Hessian Method Method) - Opt+Freq
The low frequency values have been extracted from the corresponding output file and show that the frequency calculation is complete:
Low frequencies --- -817.9780 -3.5381 -1.0455 0.0011 0.0011 0.0013 Low frequencies --- 1.1751 209.4810 395.9153 ****** 1 imaginary frequencies (negative Signs) ******
Zero-point correction= 0.152623 (Hartree/Particle) Thermal correction to Energy= 0.157982 Thermal correction to Enthalpy= 0.158927 Thermal correction to Gibbs Free Energy= 0.124116 Sum of electronic and zero-point Energies= -231.466700 Sum of electronic and thermal Energies= -231.461340 Sum of electronic and thermal Enthalpies= -231.460396 Sum of electronic and thermal Free Energies= -231.495206
An imaginary frequency was found to occur at -817.9780cm-1 which confirms the formation of the correct chair orientation transition state.
The following information was obtained following the optimization (3-21G, Hartree Fock) of a Transition State of two allyl fragments with a chair orientation:
Point Group: C2h
Energy: -231.61932242 a.u
Frozen Co-ordinated Method
Figure 14. A Gaussview image of a Transition State Optimization (Frozen Co-ordinated Method) of a Chair Orientation
The second optimization method involved freezing the transition state in the reaction co-ordinate and minimizing the remainder of the molecule which can sometimes result in a more accurate transition state structure. This is due to the fact that because the remainder of the molecule is fully relaxed after the initial optimization, the transition state optimization of the molecule can be started.
Similarly to the Hessian Method, two allyl fragments (CH2CHCH2) were initially optimized using a 3-21G - (Hatree Fock) minimal basis set. The two allyl fragments were then placed in an orientation similar to that of a chair conformation transition state with a distance of approximately 2.2Å between the terminal carbons of each fragment.
These two fragments were then optimized to a chair transition state using the Hessian Method and the force constants were recorded once the optimization had been complete.
The terminal forming/breaking bonds were frozen initially whilst the rest of the molecule was optimized and subsequently the terminal bond lengths were optimized in order to form a complete chair structure.
Results from the Log. File2Chair and gaussview summary provided below:
D Space: http://hdl.handle.net/10042/24128
Figure 15. Gaussview Summary of Optimized Chair Orientation(Frozen Co-ordinated Method) - 3-21G - Hartree Fock
Point Group: C2h
Energy: -231.61509647 a.u
Boat Transition State
QST2 Method
The optimization of a boat transition state requires a different approach to be taken in comparison to the chair transition state optimization.
Each of the two molecules of the previously optimized Ci symmetry anti-periplanar 1,5-hexadiene conformer were firstly numbered in a way that would suggest that one molecule represented the reactant and the other molecule represented the product.
Using Gaussview, an 'Opt+Freq' calculation was then ran on the two molecules with the suggested QST2 transition state optimization and a 3-21G - (Hartree Fock) minimal level basis-set.
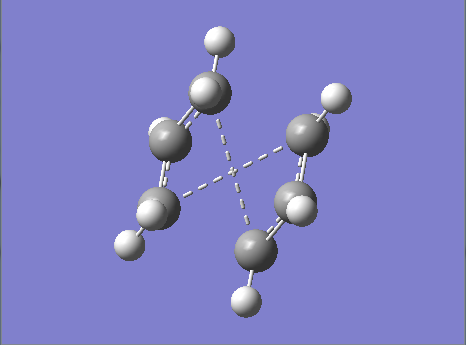
Figure 16. A Gaussview Image of a Transition State Optimization (QST2 Method) of a Boat Orientation - 3-21G - HF
It appears from the gaussview image in Figure.16 above that the optimization using the QST2 method failed as the geometries of both the reactant and product molecules were not close enough to the desired boat orientation transition state and as a result the gaussview programme simply relocated the top allyl fragment of the molecule without considering the possibility of rotation around the central bonds which make up the molecule as a whole.
This therefore resulted in a more chair-like orientation forming rather than the desired boat-like orientation as illustrated above in Figure.16.
Results from the Log. File1Boat and gaussview summary provided below:
D Space: http://hdl.handle.net/10042/24153
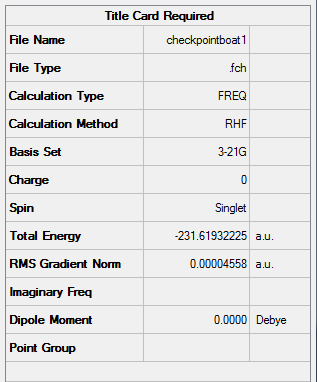
Figure 17. A Gaussview Summary of a Transition State Optimization (QST2 Method) of a Boat Orientation - 3-21G - HF
A further ammendment was made to the molecule to make the two fragments have a more boat like orientation and this involved fixing the geometries by adjusting the dihedral and bond angles of the central carbons. In particular the central C2-C3-C4-C5 dihedral angle was fixed to 0° and the two inner C2-C3-C4 and C3-C4-C5 angles were foxed to 100°.
Using Gaussview, an 'Opt+Freq' calculation was then ran on the two fragments with the new fixed geometries and with the suggested QST2 transition state optimization and a 3-21G(Hartree Fock) minimal level basis-set.
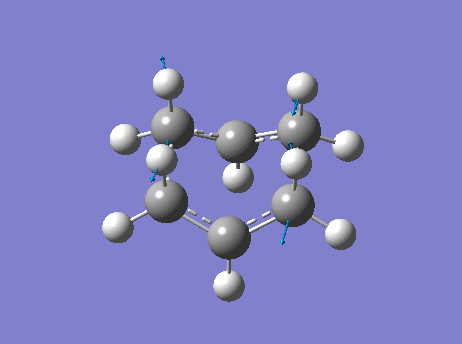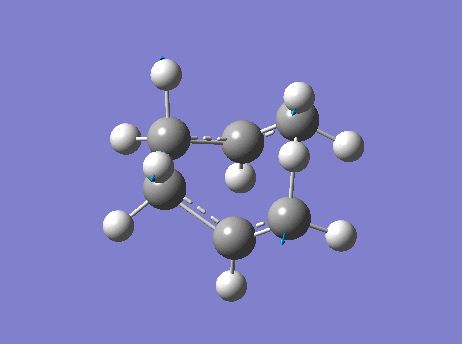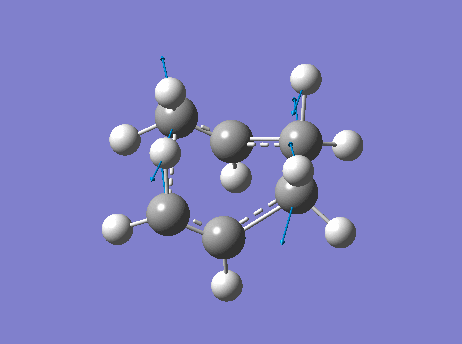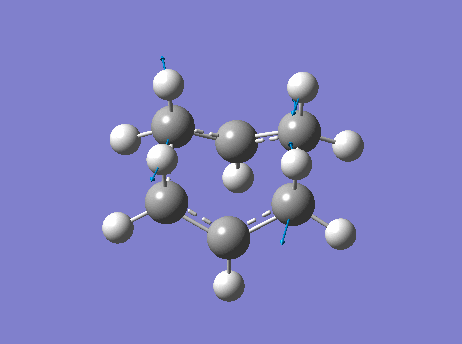
Figure 18. A Gaussview Movie of a Transition State Optimization (QST2 Method) of a Boat Orientation (Fixed Geometries)
Results from the Log. File2Boat and gaussview summary provided below:
D Space: http://hdl.handle.net/10042/24154
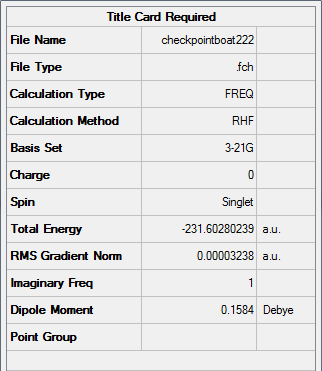
Figure 19. A Gaussview Summary of a Transition State Optimization (QST2 Method) of a Boat Orientation (Fixed Geometries)
The low frequency values have been extracted from the corresponding output file and show that the frequency calculation is complete:
Low frequencies --- -839.9283 -8.0756 -6.3114 -4.0797 -0.0009 -0.0006 Low frequencies --- 0.0004 155.0909 382.2138 ****** 1 imaginary frequencies (negative Signs) ******
Zero-point correction= 0.151880 (Hartree/Particle) Thermal correction to Energy= 0.157509 Thermal correction to Enthalpy= 0.158453 Thermal correction to Gibbs Free Energy= 0.123035 Sum of electronic and zero-point Energies= -231.450922 Sum of electronic and thermal Energies= -231.445294 Sum of electronic and thermal Enthalpies= -231.444349 Sum of electronic and thermal Free Energies= -231.479768
An imaginary frequency was found to occur at -839.9283cm-1 which confirms the formation of the correct boat orientation transition state.
The following information was obtained following the optimization (3-21G, Hartree Fock) of a Transition State of two allyl fragments with a boat orientation:
Point Group: C2v
Energy: -231.60280239 a.u
From the 'Opt+Freq' logfile. data above it is clear that the QST2 method has been a successful method in achieving an optimal transition state. There are however limitations which exist in the method such as the product and reactant structures which are inserted in the input file have to be closer to the believed transition state orientations.
An alternative more enhanced method which avoids the limitations of QST2 and is able to modify the user input files of the product, reactant and guess transition state structures relatively is called the QST3 method[2][3].
Intrinsic Reaction Co-ordinate(IRC)
It is evident from the optimised structures of the reactants and products as well as their transition state structures to distinguish whether they correspond to the 'gauche' or the 'anti-periplanar' 1,5-hexadiene structures.
An Intrinsic Reaction Co-ordinate analysis allows you to determine the local minimum point to the 'saddle' transition state. This is achieved by recording the minimum energy pathway from the transition state to this local minimum point.
The Intrinsic Reaction Co-ordinate is formed by fixing the geometry of the molecule following the section of the reaction profile with the steepest gradient potential energy surface. In this case was run on the previously optimised chair structure to determine which 1,5-hexadiene conformer the chair orientation corresponds to.
In the following optimized chair transition state analysis, the direction of the IRC was chosen due to the fact that the forward reaction of this reaction is symmetrical. For this calculation of the forward reaction, '50' steps was specified.
The calculation was then run on a HPC server - D-Space: http://hdl.handle.net/10042/24210
Chair Transition State Iteration Sequence - '50' Steps
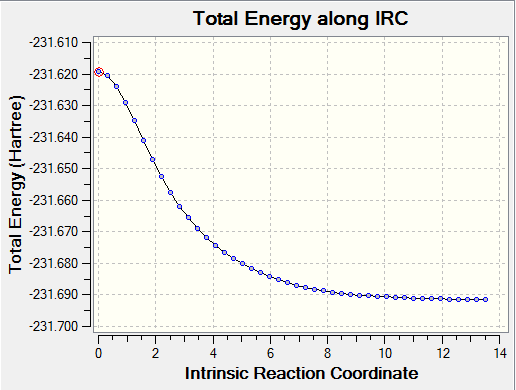
Chair Transition State Reaction Co-ordinate
The lowest Total Energy: -231.61933242 a.u
The Intrinsic Reaction Coordinate did not reach a minimum geometry using only 50 steps in this calculation and so the calculation was run again with 100 steps being computed along the reaction co-ordinate. The lowest energy resultant structure was optimized and then data from the analysis found some resemblance to the Gauche (2) conformer from Appendix 1[1].
The calculation was then run on a HPC server - D-Space: http://hdl.handle.net/10042/24221
Chair Transition State Iteration Sequence - '100' Steps
Chair Transition State Reaction Co-ordinate
The lowest Total Energy: -231.619332244 a.u
Activation Energies
In order to calculate the activation energies for the Cope rearrangement of 1,5 hexadiene via both chair and boat orientation transition structures, the structures must be reoptimized using the 6-31G - (B3LYP) higher basis set and then undergo freqency calculations.
Chair - B3LYP/6-31G(D) Optimization
Figure 20. A Gaussview Image of a Transition State Optimization of Two Allyl Fragments with a Chair Orientation - 6-31G
Results from the Log. File1Activation and gaussview summary provided below:
D Space: http://hdl.handle.net/10042/24170
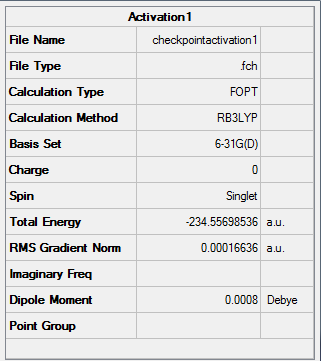
Figure 21. A Gaussview Summary of a Transition State Optimization of Two Allyl Fragments with a Chair Orientation - 6-31G
The following information was obtained following the optimization 6-31G - (Hartree Fock) of the 1,5-hexadiene molecule:
Point Group: C2h
Energy: -234.55698536 a.u
C-C Bond Length: 1.41 Å (3.s.f)
C-H Bond Length: 1.09 Å (3.s.f)
Chair - B3LYP/6-31G(D) Frequency Analysis
A vibrational analysis was carried out using the previously optimized chair orientation transition state (DFT, B3LYP, 6-31G (d)).
Results from the Log. File2ActivationFrequency and gaussview summary provided below:
D Space: http://hdl.handle.net/10042/24174
The low frequency values have been extracted from the corresponding output file and show that the frequency calculation is complete:
Low frequencies --- -564.9382 -0.0007 -0.0007 -0.0006 21.3168 26.5951 Low frequencies --- 39.4745 194.3347 268.6930 ****** 1 imaginary frequencies (negative Signs) ******
Zero-point correction= 0.142061 (Hartree/Particle) Thermal correction to Energy= 0.147980 Thermal correction to Enthalpy= 0.148924 Thermal correction to Gibbs Free Energy= 0.113178 Sum of electronic and zero-point Energies= -234.414924 Sum of electronic and thermal Energies= -234.409005 Sum of electronic and thermal Enthalpies= -234.408061 Sum of electronic and thermal Free Energies= -234.443808
The lowest "real" normal mode is found to occur at 39.4745cm-1
Boat - B3LYP/6-31G(D) Optimization
Figure 22. A Gaussview Image of a Transition State Optimization of Two Allyl Fragments with a Boat Orientation - 6-31G
Results from the Log. File2Activation and gaussview summary provided below:
D Space: http://hdl.handle.net/10042/24176
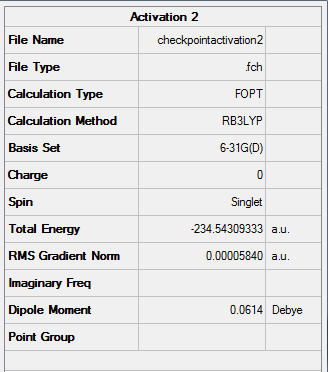
Figure 23. A Gaussview Summary of a Transition State Optimization of Two Allyl Fragments with a Boat Orientation - 6-31G
The following information was obtained following the optimization 6-31G - (Hartree Fock) of the 1,5-hexadiene molecule:
Point Group: C2v
Energy: -234.54309333 a.u
C-C Bond Length: 1.39 Å (3.s.f)
C-H Bond Length: 1.09 Å (3.s.f)
Boat - B3LYP/6-31G(D) Frequency Analysis
A vibrational analysis was carried out using the previously optimized boat orientation transition state (DFT, B3LYP, 6-31G (d)).
Results from the Log. File3ActivationFrequency and gaussview summary provided below:
D Space: http://hdl.handle.net/10042/24181
The low frequency values have been extracted from the corresponding output file and show that the frequency calculation is complete:
Low frequencies --- -530.3618 -8.3908 0.0002 0.0010 0.0010 15.4632 Low frequencies --- 17.6137 135.6121 261.7006 ****** 1 imaginary frequencies (negative Signs) ******
Zero-point correction= 0.140751 (Hartree/Particle) Thermal correction to Energy= 0.147086 Thermal correction to Enthalpy= 0.148030 Thermal correction to Gibbs Free Energy= 0.111341 Sum of electronic and zero-point Energies= -234.402342 Sum of electronic and thermal Energies= -234.396008 Sum of electronic and thermal Enthalpies= -234.395063 Sum of electronic and thermal Free Energies= -234.431752
The lowest "real" normal mode is found to occur at 17.6137cm-1
Energy Summary
A summary of the total energies in each system after each optimization at a given temperature:
[1 a.u. = 1 hartree = 627.509 kcal/mol]
| HF/3-21G | B3LYP/6-31G* | |||||
|---|---|---|---|---|---|---|
| Electronic energy (a.u.) | Sum of electronic and zero-point energies at 0 K (a.u.) | Sum of electronic and thermal energies at 298.15 K (a.u.) | Electronic energy (a.u.) | Sum of electronic and zero-point energies at 0 K (a.u.) | Sum of electronic and thermal energies at 298.15 K (a.u.) | |
| Chair TS | -231.619322 | -231.466705 | -231.461346 | -234.556983 | -234.414919 | -234.408998 |
| Boat TS | -231.602802 | -231.450929 | -231.445300 | -234.543093 | -234.402340 | -234.396006 |
| Reactant (anti2/Ci) | -231.692535 | -231.539539 | -231.5322566 | -234.611710 | -234.469203 | -234.461856 |
A summary of the activation energies in each system after each optimization at a given temperature in comparison to experimental values:
| HF/3-21G at 0 K (ΔE (kcal/mol)-1) | HF/3-21G at 298.15 K (ΔE (kcal/mol)-1) | B3LYP/6-31G* at 0 K (ΔE (kcal/mol)-1) | B3LYP/6-31G* at 298.15 K (ΔE (kcal/mol)-1) | Experimental Values [4](ΔE(kcal/mol)-1) | |
| ΔE (Chair) | 45.7 | 45.3 | 34.1 | 33.7 | 33.5 ± 0.5 |
| ΔE (Boat) | 55.6 | 50.3 | 42.0 | 37.6 | 44.7 ± 2.0 |
From the tabulated data above it is clear that the activation energies for the boat transition state are consistently alot higher than the actovation energies for the chair transition state.This therefore suggests that more thermal energy is needed for the reaction to occur via the boat structure.
Under thermodynamic conditions (high temperature), the system has the required amount of energy to equilibriate and react via the boat transition structure, but in contrast when the system is under kinetic control (low temperatures) the reaction goes via the chair transition state as this requires less energy and therefore the energy barrier is easier to overcome.
When molecules are at higher temperatures (289 K) the activation energy is lower due to the increased kinetic energy in the structures to overcome the transition state barrier compared to at lower temperatures (0 K) when only the zero point energy is available.
It is also clear from the data that the activation energy for the chair transition state is very close to the literature values. This shows the benefits and accuracy of using computational methods to carry out calculations in chemistry.
Another point worth mentioning from the data above is that the sum of electronic and zero-point energies of the structures are lower than the sum of electronic and thermal energies. This is as predicted in theory and arises because at 0K there are no thermal vibrations.
The Diels-Alder Cycloaddition
The Diels-Alder is usually used by synthetic chemists due to its specific regio- and stereo- selectivity. The Diels-Alder cycloaddition reaction is a concerted [4+2] cycloaddition involving a carbon-carbon bond forming. It occurs between a conjugated diene and an alkene dienophile and involves [4n+2] electrons forming a stable cyclic alkene.
Furthermore, the rate of these cycloadditions can be enhanced by the presence of and electrons withdrawing group on the dienophile. This electron withdrawing group lowers the energy of the π* orbital allowing overlap to be useful in this particular synthesis. This observation is built on the theory that the driving-force for a Diels-Alder reaction is responsible for the interaction of the HOMO of one reactant with the LUMO of another.
This part of the project involves studying two Diels-Alder reactions using Gaussian and GaussView 5.0 in order to carry out calculations and characterise their transition state structures as well as analyse their HOMO and LUMO orbitals. From this information, the idea of orbital symmetry and the extent of orbital overlap can be discussed and related back to each Diels-Alder cycloaddition reaction.
The two Diels-Alder reactions that will be analysed are:
1) The addition of ethylene to cis-butadiene
2) The addition of maleic anhydride to cyclohexa-1,3-diene
The Reaction of Ethylene with cis-Butadiene
Optimisation of the cis-Butadiene Fragment
Figure 24. A Gaussview Image of an Optimized cis-Butadiene Molecule - AM1
Cis-Butadiene was drawn in Gaussview 5.0 and then optimised using the AM1 semi-empirical molecular orbital method.
Results from the Log. File1Butadiene and gaussview summary provided below:
D Space: http://hdl.handle.net/10042/24236
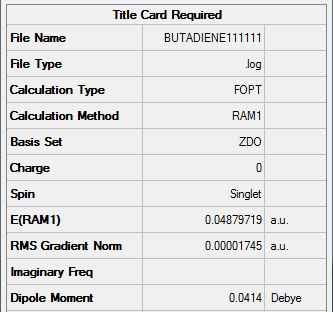
Figure 25. A Gaussview Summary of an Optimized cis-Butadiene Molecule - AM1
The data below shows the optimization has been completed:
Item Value Threshold Converged? Maximum Force 0.000030 0.000450 YES RMS Force 0.000011 0.000300 YES Maximum Displacement 0.000342 0.001800 YES RMS Displacement 0.000162 0.001200 YES Predicted change in Energy=-9.691128D-09 Optimization completed. -- Stationary point found.
The following data was gathered from the optimization:
Point Group: C2v
Energy (RAM1): 0.04879719 a.u.
Optimisation of the Ethylene Fragment
Figure 26. A Gaussview Image of an Optimized Ethylene Molecule - AM1
Ethylene was drawn in Gaussview 5.0 and then optimised using the AM1 semi-empirical molecular orbital method.
Results from the Log. File1Ethylene and gaussview summary provided below:
D Space: http://hdl.handle.net/10042/24238
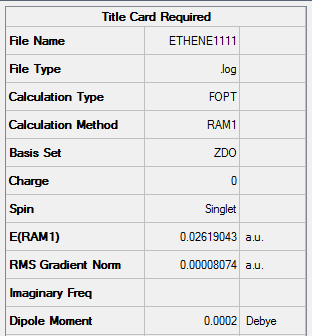
Figure 27. A Gaussview Summary of an Optimized Ethylene Molecule - AM1
The data below shows the optimization has been completed:
Item Value Threshold Converged? Maximum Force 0.000304 0.000450 YES RMS Force 0.000108 0.000300 YES Maximum Displacement 0.000833 0.001800 YES RMS Displacement 0.000390 0.001200 YES Predicted change in Energy=-1.887970D-07 Optimization completed. -- Stationary point found.
The following data was gathered from the optimization:
Point Group: D2h
Energy (RAM1): 0.02619043 a.u.
The Molecular Orbitals of Optimized cis-Butadiene and Ethylene
The Ethylene and cis-Butadiene molecules were optimized so that the symmetry for each of the reactants HOMO/LUMO could be analysed so and whether the reaction is allowed or not could be determined.
| Molecular Orbital | |
|---|---|
| cis-Butadiene HOMO | 
|
| Energy/a.u | - 0.344 |
| Symmetry | Antisymmetric |
| cis-Butadiene LUMO | 
|
| Energy/a.u | 0.017 |
| Symmetry | Symmetric |
| Ethylene HOMO | 
|
| Energy/a.u | - 0.388 |
| Symmetry | Symmetric |
| Ethylene LUMO | 
|
| Energy/a.u | 0.053 |
| Symmetry | Antisymmetric |
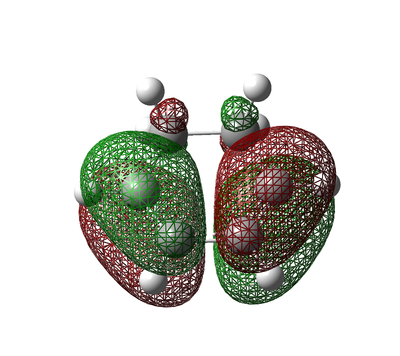
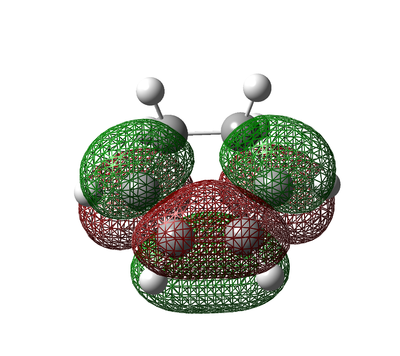
Figure 28. Ethylene and cis-Butadiene Molecular Orbitals
The table above shows how only HOMO-LUMO interactions are allowed/possible due to symmetry constraints. It is evident from the symmetries that a LUMO-LUMO interaction or a HOMO-HOMO interaction cannot occur due to a symmetry mismatch.
Fro further evidence, a frequency analysis caluclation was carried out on both the cis-Butadiene and Ethylene optimized structures. The Ethylene molecule frequency analysis showed no negative frequencies present. This confirmed that a minimum had been reached.
The cis-Butadiene molecule frequency analysis showed one negative frequency at -35.89cm-1. This negative frequency could have been caused by rotation about the backbone C-C bond that occurs readily at room temperature. The presence of a negative frequency suggests that the optimized structure is at a maximum, which in this case is expected, as the syn-periplanar arrangement results in an A1 strain.
This conformer of Butadiene may not necessarily be the most stable but as the table shows, it is the reactive conformer in respect to this particular Diels-Alder reaction.
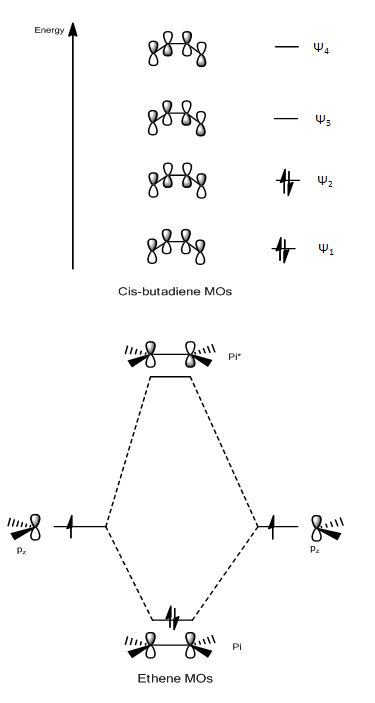
The molecular orbital diagrams above show symmetry and energy of the frontier orbital for each fragment. In order for the orbitals to overlap, the orbitals must have the same symmetry and also must be close in energy.
The symmetries of the molecular orbitals suggest that the HOMO of cis-Butadiene can overlap with the LUMO of Ethylene since both molecular orbitals are asymmetric. Similarly the HOMO of Ethylene can overlap with the LUMO of cis-Butadiene since both molecular orbitals are symmetric.
Based on the relative energy differences of the the HOMO-LUMO pairs, the antisymmetric orbitals could be deemed to overlap most strongly and therefore they can be viewed as the orbitals which contribute greatest to the transition state. However, the energy differences are fairly close (0.40484 a.u and 0.39665 a.u) and therfore it is necessary to analyse the transition state further.
Diels Alder Reaction Transition State Optimization and Frequency Analysis
Having carried out both the frequency anaylsis and optimization calculations both of the optimized structures (Cis-Butadiene and Ethylene) were orientated 2.2Å away from each other in Gaussview 5.0.
The Frozen Co-ordinate method was the used. This resulted in the terminal carbons of each molecule being frozen and the transition state being optimised using the AM1 semi-empirical molecular orbital method. After the optimization calculation had been carried out, the bond co-ordinates were unfrozen and the hessian force constant matrix was computed using a berny transition state optimization method to perform an Opt+Freq calculation using a silmilar basis set.
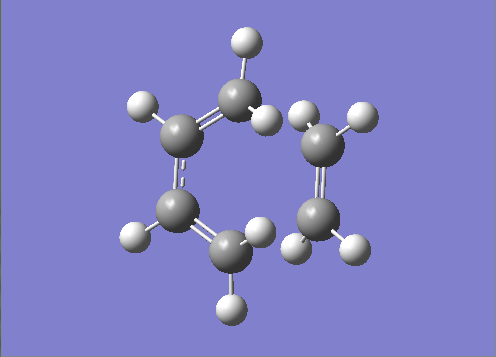
Figure 29. A Gaussview Image of the Newly Orientated cis-Butadiene and Ethylene Molecules - AM1
Results from the Log. File1Mix and gaussview summary provided below:
D Space: http://hdl.handle.net/10042/24250
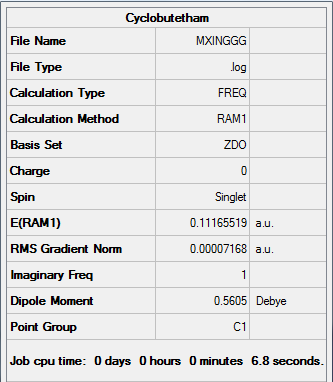
Figure 30. A Gaussview Summary of Optimized cis-Butadiene and Ethylene Fragments - AM1
The low frequency values have been extracted from the corresponding output file and show that the frequency calculation is complete:
Low frequencies --- -955.0032 -7.6989 -5.8876 -0.0049 -0.0031 0.0205 Low frequencies --- 4.1403 146.5954 246.8236 ****** 1 imaginary frequencies (negative Signs) ******
Zero-point correction= 0.141621 (Hartree/Particle) Thermal correction to Energy= 0.147800 Thermal correction to Enthalpy= 0.148744 Thermal correction to Gibbs Free Energy= 0.112357 Sum of electronic and zero-point Energies= 0.253276 Sum of electronic and thermal Energies= 0.259455 Sum of electronic and thermal Enthalpies= 0.260399 Sum of electronic and thermal Free Energies= 0.224012
The following data was gathered from the optimization:
Point Group: C1
Energy: 0.11165519 a.u
An imaginary frequency was found to occur at -955.00cm-1 which suggests the formation of a transition state structure.
Figure 31. A Gaussview Movie of the Imaginary Frequency at -955.00cm-1
From the imaginary frequency movie above it is clear how the ethylene molecule comes in from below the butadiene in order to align the HOMO/LUMO orbitals of each molecule which have the same symmetry allowing them to interact to form bonds.
Figure 32. A Gaussview Movie of the Lowest Frequency Real Vibration at -146.59cm-1
The lowest frequency real vibration is found at 146.57cm-1 and corresponds to a twist about the terminal 'C-C bond' of each molecule.
Bond Length Comparison
The transition state terminal bond length of the two fragments together was found to be relatively large in comparison to the literature values [6], showing that a C-C bond has not yet formed between the two fragments. The terminal bond lengths however waere found to be less than double the Van der Waals radius of a carbon atom suggesting that there is some interaction between the orbitals. This proides further evidence to suggest that this is the transition state for the Diels Alder [4+2] cycloaddition reaction.
| S-E/AM1 | Literature Values [7] | |
|---|---|---|
| Terminal Bond Length (Å) | 2.12 | 2.27 |
| cis-Butadiene C-C Bond Length (Å) | 1.41 | 1.39 |
| Ethylene C-C Bond Length (Å) | 1.39 | 1.38 |
Figure 33. Comparison of Transition State Structures with Literature
Comparing the bond lengths of the calculation methods allows you to determine the nature of the transition state produced in the Diels-Alder cycloaddition reaction.
The terminal atoms of each molecule in the transition state eventually form a new single sigma bond between each other forming one molecule. From literature, the typical bond length of a sp3-sp3 C-C bond is 1.53 Å[6]. The DFT transition state terminal bond length is clearly longer than the semi-empirical transition state terminal bond length.
The large difference between the transition state bond lengths and the product bond lengths suggests that the DFT transition state structure is an earlier transition state than the semi-empirical transition state. In the semi-empirical transiton state, as expected, the double bonds of the Ethylene and cis-Butadiene fragments are longer than typical carbon-carbon double bond [1.34 Å[6]] with a value of 1.38-1.39 Å but not as long as a carbon-carbon single bond.
In the product state the central carbon-carbon cis-Butadiene single bond will correspond to a carbon-carbon double bond. It is therfore expected for this bond length to shorten in the transition state structure. The bond lengths in the table above are much closer to the product form indicating the transition states are late and are more likely to be in the product channel than the reactant channel.
Diels Alder Reaction Transition State Molecular Orbitals
| Molecular Orbital | |
|---|---|
| Mixed HOMO | 
|
| Energy/a.u | - 0.324 |
| Symmetry | Antisymmetric |
| Mixed LUMO | 
|
| Energy/a.u | 0.023 |
| Symmetry | Symmetric |
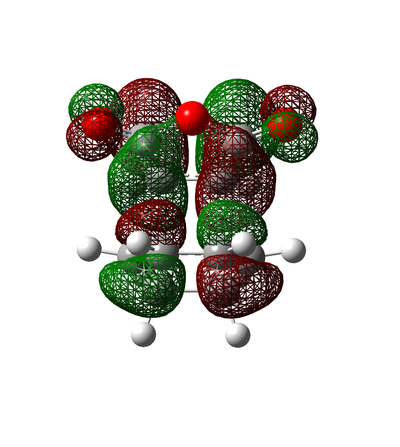
Figure 34. Combined Ethylene and cis-Butadiene Molecular Orbitals
The molecular orbital symmetry infers that the fragment orbitals used to constitute the molecular orbital as a whole are both symmetric with respect to the plane of symmetry. By analysing the molecular orbitals generated before each of the fragments were optimized and comparing them to the molecular orbitals formed once the two fragments were combined can help make an estimation for which orbitals they integrate into.
It is evident from the HOMO molecular orbital that it is antisymmetric and as a result of the overlap of the HOMO of cis-Butadiene and the LUMO of Ethylene of this transition state. The images above of the HOMO molecular obrital shows the C-C σ bonding orbitals formed in the reaction.
The LUMO on the other hand is symmetric with respect to the plane of symmetry as a result of the combination of the HOMO of ethylene and the LUMO of cis-butadiene and has more modal nodes present than that of the HOMO molecular orbital and hence has a more anti-bonding interaction. The images of the LUMO molecular orbital shows the formation of the σ* antibonding orbitals formed in the reaction.
The Reaction of Cyclohexa-1,3-diene with Maleic Anhydride
The second Diels-Alder cycloaddition reaction involved reacting Cyclohexa-1,3-diene with Maleic Anhydride. This reaction typically proceeds to give an endo and exo product. The endo product forms under kinetic control as the major product (99:1 ratio [8]). The exo product therefore being the thermodynamic product has a higher energy tranisiton state than the endo product. The use of computational calculations and analysis via Gaussian and Gaussview 5.0 will be used to why the endo adduct is the preferred product.
Figure 35. Reaction Co-ordinate for Reaction of Cyclohexa-1,3-diene with Maleic Anhydride
Optimization of the Cyclohexa-1,3-diene Fragment
Figure 36. A Gaussview Image of an Optimized Cyclohexa-1,3-diene Molecule - AM1
Cyclohexa-1,3-diene was drawn in Gaussview 5.0 and then optimised using the AM1 semi-empirical molecular orbital method.
Results from the Log. FileCyclo1 and gaussview summary provided below:
D Space: http://hdl.handle.net/10042/24298
Figure 37. A Gaussview Summary of an Optimized Cyclohexa-1,3-diene Molecule - AM1
Data below shows calculation went to completion.
Item Value Threshold Converged? Maximum Force 0.000151 0.000450 YES RMS Force 0.000037 0.000300 YES Maximum Displacement 0.000628 0.001800 YES RMS Displacement 0.000184 0.001200 YES Predicted change in Energy=-1.353767D-07 Optimization completed. -- Stationary point found.
The following data was gathered from the optimization:
Point Group: C2v
Energy (RAM1): 0.02795805 a.u.
Optimization of the Maleic Anhydride Fragment
Figure 38. A Gaussview Image of an Optimized Maleic Anhydride Molecule - AM1
Maleic Anhydride was drawn in Gaussview 5.0 and then optimised using the AM1 semi-empirical molecular orbital method.
Results from the Log. FileMaleic1 and gaussview summary provided below:
D Space: http://hdl.handle.net/10042/24299
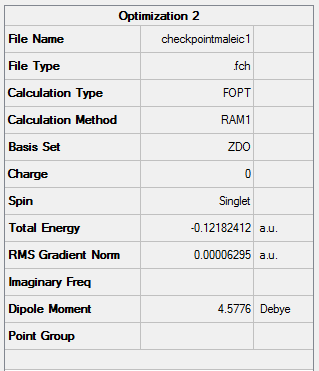
Figure 39. A Gaussview Summary of an Optimized Maleic Anhydride Molecule - AM1
Data below shows calculation went to completion.
Item Value Threshold Converged? Maximum Force 0.000159 0.000450 YES RMS Force 0.000050 0.000300 YES Maximum Displacement 0.001002 0.001800 YES RMS Displacement 0.000269 0.001200 YES Predicted change in Energy=-1.399772D-07 Optimization completed. -- Stationary point found.
The following data was gathered from the optimization:
Point Group: C2v
Energy (RAM1): -0.12182412 a.u.
Molecular Orbitals of Optimized Cyclohexa-1,3-diene and Maleic Anhydride
The Cyclohexa-1,3-diene and Maleic Anhydride molecules were optimized so that the symmetry for each of the reactants HOMO/LUMO could be analysed so and whether the reaction is allowed or not could be determined.
| Molecular Orbital | |
|---|---|
| Cyclohexa-1,3-diene HOMO | 
|
| Energy/a.u | - 0.321 |
| Symmetry | Antisymmetric |
| Cyclohexa-1,3-diene LUMO | 
|
| Energy/a.u | -0.059 |
| Symmetry | Symmetric |
| Maleic Anhydride HOMO |
|
| Energy/a.u | - 0.442 |
| Symmetry | Symmetric |
| Maleic Anhydride LUMO | 
|
| Energy/a.u | 0.053 |
| Symmetry | Antisymmetric |
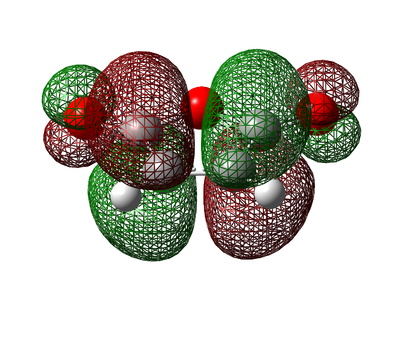
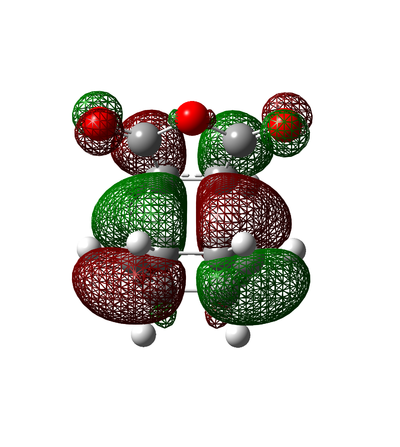
Figure 40. Cyclohexa-1,3-diene and Maleic Anhydride Molecular Orbitals
Similarly to the case of cis-Butadiene & Ethylene, only orbitals of the same symmetry can interact. This means the cyclohexadiene LUMO and the maleic anhydride HOMO can interact to form an overall symmetric product or suqsequently the cyclohexadiene HOMO and the maleic anhydride LUMO can interact to form an overall antisymmetric product. Both interactions form a plausible transition state.
The energies of the molecular orbitals indicate that the LUMO of the maleic anhydride is low lying as a result of the large HOMO-LUMO gap of maleic anhydride and as a result is able to accept electron density from the HOMO of the cyclohexadiene.
On the other hand the cyclohexadiene cannot accept electron density from the maleic anhydride as easily as theory would suggest. Nevertheless, this favourable HOMO-LUMO interaction is also allowed due the orbitals having the same symmetry also a similar energy.
Diels Alder Reaction Transition State Optimization and Frequency Analysis
Having carried out both the frequency anaylsis and optimization calculations both of the optimized structures (Cyclohexa-1,3-diene and Maleic Anhydride) were orientated 2.2Å away from each other in Gaussview 5.0.
The Frozen Co-ordinate method was the used. This resulted in the terminal carbons of each molecule being frozen and the transition state being optimised using the AM1 semi-empirical molecular orbital method. After the optimization calculation had been carried out, the bond co-ordinates were unfrozen and the hessian force constant matrix was computed using a berny transition state optimization method to perform an Opt+Freq calculation using a silmilar basis set.
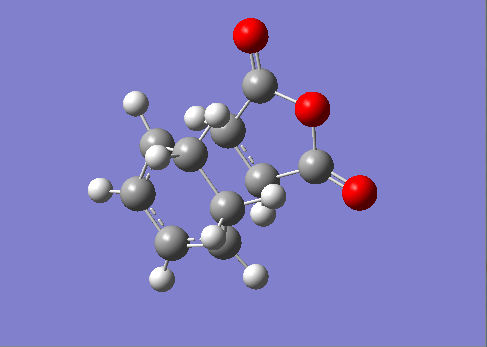
Figure 41. A Gaussview Image of the Newly Orientated Cyclohexa-1,3-diene and Maleic Anhydride Molecules - AM1
Exo Transition State
Results from the Log. File1EXO and gaussview summary provided below:
D Space: http://hdl.handle.net/10042/24304
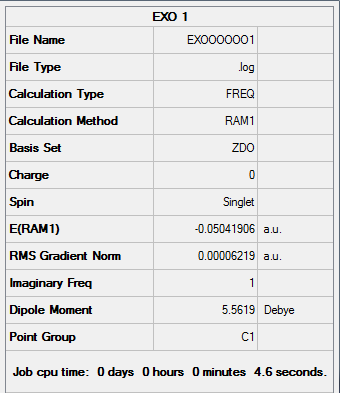
Figure 42. A Gaussview Summary of Exo Transtion State - AM1
The low frequency values have been extracted from the corresponding output file and show that the frequency calculation is complete:
Low frequencies --- -812.5227 -0.3597 -0.1544 -0.0048 2.9187 4.0604 Low frequencies --- 5.5351 61.0283 124.0240 ****** 1 imaginary frequencies (negative Signs) ******
Zero-point correction= 0.185301 (Hartree/Particle) Thermal correction to Energy= 0.195300 Thermal correction to Enthalpy= 0.196244 Thermal correction to Gibbs Free Energy= 0.149543 Sum of electronic and zero-point Energies= 0.134882 Sum of electronic and thermal Energies= 0.144881 Sum of electronic and thermal Enthalpies= 0.145825 Sum of electronic and thermal Free Energies= 0.099124
The following data was gathered from the optimization:
Point Group: C1
Energy: -0.05041906 a.u
"Forming" Bond Length: 2.17Å
An imaginary frequency was found to occur at -812.52cm-1 which suggests the formation of an Exo transition state structure.
Figure 43. A Gaussview Movie of the Imaginary Frequency at -812.52cm-1
Exo Transition State IRC
In the following optimized Exo transition state analysis, the direction of the IRC was chosen due to the fact that the forward reaction of this reaction is symmetrical. For this calculation of the forward reaction, '50' steps was specified.
The calculation was then run on a HPC server - D-Space: http://hdl.handle.net/10042/24306
Exo Transition State Iteration Sequence - '50' Steps
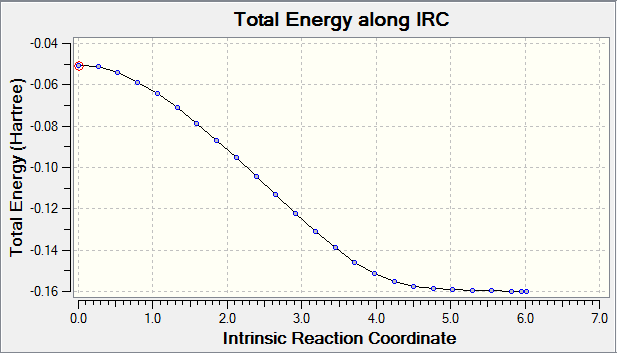
Exo Transition State Reaction Co-ordinate
Endo Transition State
Results from the Log. File1ENDO and gaussview summary provided below:
D Space: http://hdl.handle.net/10042/24308
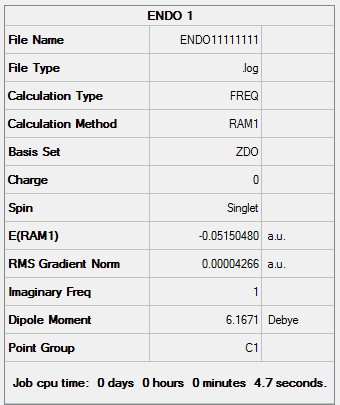
Figure 44. A Gaussview Summary of Endo Transtion State - AM1
The low frequency values have been extracted from the corresponding output file and show that the frequency calculation is complete:
Low frequencies --- -807.1405 -0.8736 -0.2615 -0.0104 0.8959 1.7321 Low frequencies --- 2.4989 62.4809 111.7886 ****** 1 imaginary frequencies (negative Signs) ******
Zero-point correction= 0.185000 (Hartree/Particle) Thermal correction to Energy= 0.195188 Thermal correction to Enthalpy= 0.196132 Thermal correction to Gibbs Free Energy= 0.148858 Sum of electronic and zero-point Energies= 0.133495 Sum of electronic and thermal Energies= 0.143683 Sum of electronic and thermal Enthalpies= 0.144627 Sum of electronic and thermal Free Energies= 0.097353
The following data was gathered from the optimization:
Point Group: C1
Energy: -0.05150480 a.u
"Forming" Bond Length: 2.16Å
An imaginary frequency was found to occur at -807.14cm-1 which suggests the formation of an Endo transition state structure.
Figure 45. A Gaussview Movie of the Imaginary Frequency at -807.14cm-1
Endo Transition State IRC
In the following optimized Endo transition state analysis, the direction of the IRC was chosen due to the fact that the forward reaction of this reaction is symmetrical. For this calculation of the forward reaction, '50' steps was specified.
The calculation was then run on a HPC server - D-Space: http://hdl.handle.net/10042/24322
Endo Transition State Iteration Sequence - '50' Steps
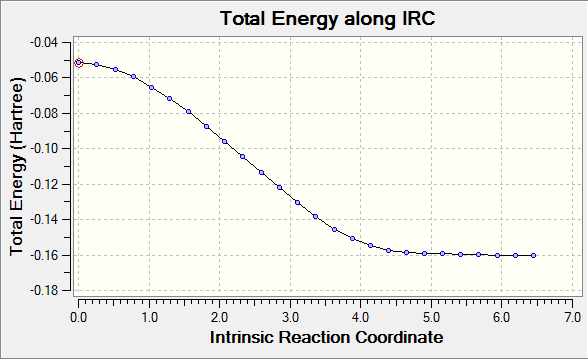
Endo Transition State Reaction Co-ordinate
Comparison Between the Endo and Exo Transition States
Bond Lengths
The image below compares the set of bond lengths for the Endo adduct and the Exo adduct:
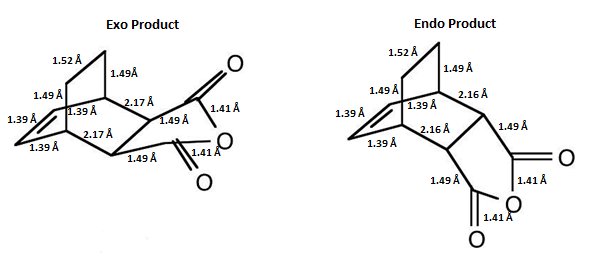
The only difference in bond length is that of the carbon joining the Cyclohexa-1,3-diene and Maleic Anhydride molecules and the carbon adjacent to it which makes up the Cyclohexa-1,3-diene molecule(inter-fragment bond length). In the Exo adduct the carbon-carbon bond length is 2.17Å whereas in the Endo adduct the carbon-carbon bond length is 2.16Å. This small difference in bond length is due to the different orientations of the Maleic Anhydride in each adduct. This slight difference in geometry is important in explaining why the Exo adduct is thermodynamically favoured and why the Endo adduct is the kinetic product. This difference is expected in the transition states of each adduct but it is difficult to define whether the Exo and Endo adducts are early or late transition states due to fact that there is some discrepancy with the adduct bond lengths and those reported in literature.
The reason why the Exo adduct is thermodynamically favoured over the Endo adduct can be explained by the through space distance between the Cyclohexa-1,3-diene molecule and Maleic Anydride in the transition states. It is clear that the distance between the Cyclohexa-1,3-diene molecule and Maleic Anydride molecules is longer in the Exo adduct trasition state in comparison to the Endo adduct transition state (2.17 Å compared to 2.16 Å ). This indicates that the Exo adduct experiences less steric repulsion between the two fragments and hence it is more stable(lower energy).
Despite the fact that the Exo adduct is thermodynamically favored, the Endo adduct is predominately favored in the Diels-Alder reaction. This is beacuse the Endo transition state adduct is the kinetic product and therefore the activation energy of its energy pathway is lower than that of the Endo transition state adduct.
Activation Energies
| Parameter | Exo | Endo |
|---|---|---|
| Activation Energy/a.u | -0.05041906 | -0.05150480 |
| Activation Energy/kCal mol-1 | 34.30 | 33.71 |
Figure 46. Activation Energies of the Endo and Exo Transition States
The activation energy values reflect the amount of energy required to overcome the energy barrier in order for product to form.
The fact that the Exo adduct transition state activation energy is higher than that of the Endo adduct transition state suggesting that the rate of formation of the Endo adduct would be much faster. This also helps explain the reasoning behind the regioselectivity of this reaction under kinetic control.
The reason for the enhanced stability of the Endo adduct transition state is due to secondary orbital overlap (SOO) in the frontier molecular orbitals. In the Endo adduct transition state there is much more secondary orbital overlap (SOO) compared to the Exo adduct and as a result there is much greater stability.
The image below displays how secondary orbital interactions are only present in the Endo adduct transition state and help stabilise it causing it to be lower in energy.
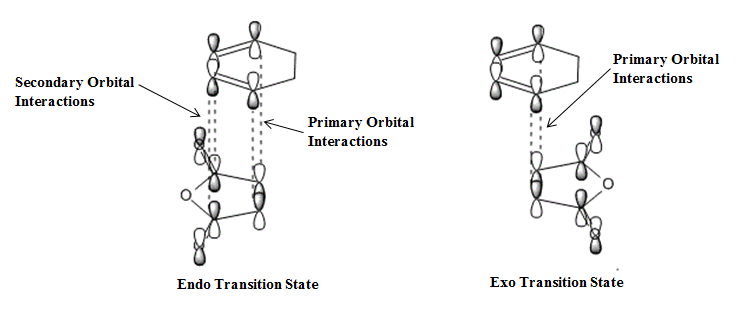
Figure 47. Endo and Exo Transition State Orbital Interactions
These secondary orbital overlaps can also be seen in the HOMO of the Exo and Endo adducts below in Figure.48.
Four of the π orbitals on HOMO of the cyclohexadiene interact with the LUMO of Maleic Anhydride in the Endo adduct transition state compared to the main bonding orbitals interacting in the Exo adduct transition state. The Endo adduct transition state is therefore stabilised resulting in the formation of the Endo product being more favourable regardless of other factors associated with the products such as ring strain and steric repulsion.
Molecular Orbitals
| Molecular Orbital | |
|---|---|
| Exo Adduct HOMO | 
|
| Energy/a.u | - 0.343 |
| Symmetry | Antisymmetric |
| Exo Adduct LUMO | 
|
| Energy/a.u | -0.040 |
| Symmetry | Antisymmetric |
| Endo Adduct HOMO | 
|
| Energy/a.u | - 0.345 |
| Symmetry | Antisymmetric |
| Endo Adduct LUMO | 
|
| Energy/a.u | -0.036 |
| Symmetry | Antisymmetric |
Figure 47. Exo and Endo Molecular Orbitals
Itis evident form the table above that the HOMO of Cyclohexa-1,3-diene interacts with the LUMO of Maleic Anhydride as both of the molecular orbitals are antisymmetric.
The energies of the molecular orbitals suggest that the Exo adduct is the preferred product over the Endo adduct since the Exo adduct is lower overall in energy and doesn't have the unfavorable interactions that the Endo product has. This is despite the fact that the Endo transition state is lower in energy than the Exo transition state.
The HOMO molecular orbital for the endo adduct is higher in energy due to the fact that the antibonding π* orbitals on the oxygen atoms in the carbon-oxygen double bond are seen to be interacting repulsively with the antibonding π* orbitals of the carbon-carbon double bonds on cyclohexadiene fragment. This is the reason how the endo adduct adopts it's shape and the reason why there is increased strain on the molecule.
In comarison, the Exo adduct doesn't have this repulsive interaction and therefore as suggested by theory it should be the more stable adduct (thermodynamic product). Although the Exo adduct is more stable it has a higher activation energy due to it's higher energy transition state and lower energy final product. Under kinetic control, the pathway with the lowest activation energy and the most stable transition state forms fastest and in the case of this reaction this is the Endo adduct even though it is the least stable product.
Conclusion
The use of computational methods to predict transition state structures has proven to very useful in research as transition state structures cannot be seen using ordinary scientific metods. Observing the optimisation and frequency analysis data from transition state structures obtained from computational methods allows chemists to predict the outcome of various reactions. The data obtained from the transition states has consequently proven key in understanding the various kinetic and thermodynamic observations in reactions such as reaction rates and reaction enthalpies.
The first reaction in this project involved carrying out calculations and analysing the Cope Rearrangement. The calculations carried out on the rearrangement reaction showed that the Cope Rearrangement proceeds via a stabilised chair transition state.
The second reaction in the project involved carrying out calculations and analysing the Diels-Alder reaction. The first Diels-Alder reaction between Ethylene and cis-Butadiene was shown to proceed via an enveloped transition state and the reaction pathway of this reaction was dependent on the structures of the HOMO/LUMO molecular orbitals. The concept of orbital overlap was further reinstated in the second reaction between Cyclohexa-1,3-diene and Maleic Anhydride reaction where it was discovered that the endo structure predominates under kinetic conditions due to favoring secondary orbital overlap stabilising the transition state.
Overall the use of computational chemistry is extremely useful in allowing you to predict and analyse transition states, vibrational frequencies and reaction pathways for all types of reactions.
Ammendments
Possible ammendments include considering the solvent effects, temperature and pressure, since these factors were ignored when carrying out the calculations using gaussian. This will help explain whether the temperature and solvent effects on the secondary orbital interactions help stabilise the transition states.
It may also have been useful to run the calculations using other methods (e.g DFT, Hartree Fock) in order to compare the results and decide whether the energy pathway changes.
References
1. 'Labscript'
2. C. Peng and H. B. Schlegel, "Combining Synchronous Transit and Quasi-Newton Methods to Find Transition States," Israel J. of Chem., 33, 449 (1993).
3. C. Peng, P. Y. Ayala, H. B. Schlegel and M. J. Frisch, "Using Redundant Internal Coordinates to Optimize Equilibrium Geometries and Transition States," J. Comp. Chem., 17, 49 (1996).
4. 'Labscript'
5. http://www.chem.wayne.edu/~hbs/chm6440/PES.html
6. N.C. Craig, P. Groner, D.C. McKean, J. Phys. Chem. A., 2006, 110, 7461-7469.
7. Goldstein, E.; Beno, B.; Houk, K. N.; J. Am. Chem. Soc., 1996, 118, 6036-6043.
8. N.C. Craig, P. Groner, D.C. McKean, J. Phys. Chem. A., 2006, 110, 7461-7469.