Physical Computational Chemistry

Introduction

This computational experiment is about characterising the transition structures for the Cope rearrangement and Diels Alder cycloaddition reactions. In this experiment, the transition structures in larger molecules (such as the transition structure of orto-thalic acid anhydride) were shown and studied. The Schrodinger equation was solved numerically, using the molecular orbital-based method, by locating the transition state structures (based on the local shape of the potential energy surface). Reaction paths and activation energies were also be calculated in this experiment.

Hart-tree optimisation

1,5-hexadiene (anti)

The total energy for the "anti" linkage of 1,5-hexadiene is -231.69253 a.u. and the point group for the structure is C_i.

This is the Hart-Tree optimised 1,5-hexadiene (anti) file: opt_anti.

Summary table

Summary	Results
File name	1,5-hexadiene_optimisation_anti2
File type	.log
Calculation Type	FOPT
Calculation Method	RHF
Basis set	3-21G
Charge	0
Spin	Singlet
E(RHF)	-231.69254 a.u.
RMS Gradient Norm	0.00003 a.u.
Imaginary Freq
Dipole moment	0.00 Debye
Point Group	C_i

1,5-hexadiene (gauche)

The gauche conformation should be higher in energy because the hydrogens are nearer to each other in the gauche confromation - this means that the hydrogens are in a sterically less favourable position in this conformation. This is indeed the case; the total energy for the gauche conformation is -231.68916 a.u. (in comparison to -231.69254 for the - previous - anti-conformer). The point group for the gauche conformer is C₁.

This is the Hart-Tree optimised 1,5-hexadiene (gauche) file: opt_gauche.

Summary table

Summary	Results
File name	1,5-hexadiene_optimisation_gauche
File type	.log
Calculation Type	FOPT
Calculation Method	RHF
Basis set	3-21G
Charge	0
Spin	Singlet
E(RHF)	-231.68916 a.u.
RMS Gradient Norm	0.00000 a.u.
Imaginary Freq
Dipole moment	0.54 Debye
Point Group	C₁

1,5-hexadiene (anti)

This is the Hart-Tree optimised 1,5-hexadiene (anti) file: opt_anti_new.

This anti conformer has a total energy of -231.69097 a.u. and a point group of C₁.

Summary table

Summary	Results
File name	1,5-hexadiene_optimisation_anti
File type	.log
Calculation Type	FOPT
Calculation Method	RHF
Basis set	3-21G
Charge	0
Spin	Singlet
E(RHF)	-231.69097 a.u.
RMS Gradient Norm	0.00001 a.u.
Imaginary Freq
Dipole moment	0.30 Debye
Point Group	C₁

Lowest energy conformer of 1,5-hexadiene

The lowest energy conformer will have the two ethene groups anti-periplanar with respect to each other. The total energy of the lowest energy conformer is -231.6926 a.u. and the point group of the structure is C₂.

This is the Hart-Tree optimised lowest energy conformer of 1,5-hexadiene file: opt_lec.

Summary table

Summary	Results
File name	1,5-hexadiene_optimisation_anti1
File type	.log
Calculation Type	FOPT
Calculation Method	RHF
Basis set	3-21G
Charge	0
Spin	Singlet
E(RHF)	-231.69260 a.u.
RMS Gradient Norm	0.00002 a.u.
Imaginary Freq
Dipole moment	0.20 Debye
Point Group	C₂

DFT optimisation of anti2

The basis set for the (DFT) optimisation was changed from 3-21G to B3LYP/6-31G(d). The total energy changed from -231.69254 a.u. to -234.61171 a.u.. The point group for the two anti2 structures is still C_i, but the structure that was derived with higher level of theory is lower. The (tetrahedral) angle is 109.40 degrees, for the Hart-tree optimised anti2 conformer, and 109.61 degrees, for the DFT optimised conformer; the larger tetrahedral angle for the DFT optimised anti2 conformer is the reason for why it calculates a lower energy (there's less steric repulsion).

This is the DFT optimised anti2 conformer of 1,5-hexadiene file: opt_anti2.

This is the frequency file: freq_anti2.

Summary table

Summary	Results
File name	1,5-hexadiene_frequency_anti2_B3LYP6-31Gd
File type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis set	6-31G(d)
Charge	0
Spin	Singlet
E(RB3LYP)	-234.61171 a.u.
RMS Gradient Norm	0.00000 a.u.
Imaginary Freq
Dipole moment	0.00 Debye
Point Group	C_i

Comparison with appendix

The anti-periplanar conformer with a total energy of -231.69254 a.u. is the anti2 conformer; the anti-periplanar conformer with a total energy of 231.69260(236) a.u. is the anti1 conformer; the gauche conformer shown is the gauche6 conformer; and the anti-periplanar conformer with a total energy of -231.69097 a.u. is the anti4 conformer.

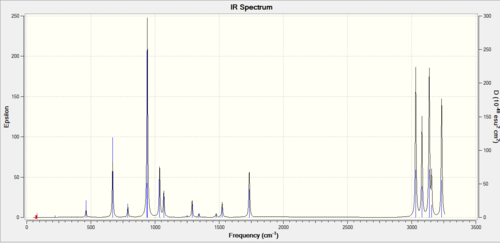
Low frequencies

Low frequencies ---   -9.2018   -0.0006   -0.0005   -0.0005    3.4135   13.2274
Low frequencies ---   74.4382   81.0434  121.4893

Item table

Item                        Value     Threshold  Converged?
 Maximum Force            0.000019     0.000450     YES
 RMS     Force            0.000006     0.000300     YES
 Maximum Displacement     0.000239     0.001800     YES
 RMS     Displacement     0.000076     0.001200     YES
 Predicted change in Energy=-3.992139D-09
 Optimization completed.
    -- Stationary point found.

IR spectrum

Thermochemistry at 298.15 K

Sum of electronic and zero-point Energies= -234.469203 (Hartree/Particle)
Sum of electronic and thermal Energies= -234.461858(Hartree/Particle)
Sum of electronic and thermal Enthalpies= -234.460913(Hartree/Particle)
Sum of electronic and thermal Free Energies= -234.500775(Hartree/Particle)

Thermochemistry at 0 K

Sum of electronic and zero-point Energies= -234.469203 (Hartree/Particle)
Sum of electronic and thermal Energies= -234.597023(Hartree/Particle)
Sum of electronic and thermal Enthalpies= -234.597023(Hartree/Particle)
Sum of electronic and thermal Free Energies= -234.595898(Hartree/Particle)

The Hart-tree optimisation of the "Chair" and "Boat" Transition Structures

Chair

This is the Hart-tree optimised anti2 conformer of 1,5-hexadiene file: opt_chair.

Summary	Results
File name	chair_ts_ally_fragments_optimisation
File type	.log
Calculation Type	FREQ
Calculation Method	RHF
Basis set	3-21G
Charge	0
Spin	Singlet
E(RHF)	-231.61932 a.u.
RMS Gradient Norm	0.00005 a.u.
Imaginary Freq
Dipole moment	0.00 Debye
Point Group	C_2h

Optimising using the frozen coordinate method

Summary	Results
File name	CHAIR_TS_ALLY_FRAGMENTS_OPTIMISATION_REDUNDANT
File type	.log
Calculation Type	FOPT
Calculation Method	RHF
Basis set	3-21G
Charge	0
Spin	Singlet
E(RHF)	-231.61611 a.u.
RMS Gradient Norm	0.00510 a.u.
Imaginary Freq
Dipole moment	0.01 Debye
Point Group	C₂

opt_chair_redundant.

Summary table for the Hessian optimised chair transition state

Summary	Results
File name	CHAIR_TS_ALLY_FRAGMENTS_OPTIMISATION_hessian
File type	.log
Calculation Type	FOPT
Calculation Method
Basis set
Charge	0
Spin	Singlet
E	-231.50884 a.u.
RMS Gradient Norm	0.02035 a.u.
Imaginary Freq
Dipole moment	0.28 Debye
Point Group	C₁

opt_chair_hessian.

Comparison between the "Hessian" optimised transition state and the "NoEigen" optimisation of the chair transition state.

The "Hessian" optimised transition state structure has an energy of -231.5088 a.u., this is higher in energy than the total energy of the "NoEigen" optimisation of the transition state (which has a total energy of -231.6913 a.u.). The NoEigen optimisation structure has a point group of C_2h, while the Hessian optimised structure has a point group of C₁. The bond forming/breaking lengths for the Hessian structure is 2.1587 and 2.2560 Å; the bond forming/breaking lengths for the NoEigen structure are both 2.0187 Å.

Boat

Summary table

Summary	Results
File name	QST_optimised
File type	.log
Calculation Type	FREQ
Calculation Method	RHF
Basis set	3-21G
Charge	0
Spin	Singlet
E(RHF)	-231.60280 a.u.
RMS Gradient Norm	0.00011 a.u.
Imaginary Freq	1
Dipole moment	0.16 Debye
Point Group	C_2v

This is the failed job file: opt_freq_failed_chair.

This is the successful job file: opt_freq_successful_chair.

Item table

Item                      Value       Threshold    Converged?
 Maximum Force            0.000216     0.000450     YES
 RMS     Force            0.000052     0.000300     YES
 Maximum Displacement     0.001770     0.001800     YES
 RMS     Displacement     0.000482     0.001200     YES
 Predicted change in Energy=-6.861800D-07
 Optimization completed.
    -- Stationary point found.

Low frequencies

Low frequencies --- -839.1802   -9.2984   -0.0003    0.0007    0.0009    4.5924
Low frequencies ---    6.3001  154.7768  381.3735

QST3

This is the imaginary vibrational mode (at -840 cm^-1) for the boat transition state.

The difference between the QST2 method and the QST3 method is that QST2 requires two molecule specifications, for the reactant and product, as its input, while QST3 requires three molecule specifications: the reactant, the product, and an initial structure for the transition state (in that exact order).

The QST3 optimised boat conformer has an imaginary vibrational mode at -840 cm^-1; the QST2 optimised boat conformer, as mentioned previously, has an imaginary vibrational mode at -839 cm^-1; the total energy of the QST3 optimised boat conformer is the same as that of the QST2 optimised boat conformer (-231.60280 a.u.).

Summary table

Summary	Results
File name	QST3_optimised
File type	.log
Calculation Type	FREQ
Calculation Method	RHF
Basis set	3-21G
Charge	0
Spin	Singlet
E(RHF)	-231.60280 a.u.
RMS Gradient Norm	0.00002 a.u.
Imaginary Freq	1
Dipole moment	0.16 Debye
Point Group	C_2v

QST3‎

Item table

Item                          Value      Threshold     Converged?
Maximum Force               0.000069      0.000450        YES
RMS Force                   0.000013      0.000300        YES
Maximum Displacement        0.001002      0.001800        YES
RMS Displacement            0.000221      0.001200        YES
Predicted change in Energy=-4.237594D-08
Optimization completed.
-- Stationary point found.

Low frequencies

Low frequencies --- -839.8438 -5.7454 -4.0603 -0.0008 -0.0006 -0.0005
Low frequencies --- 0.5241 155.1918 382.0328

Intrinsic reaction coordinate (Chair)

The intrinsic reaction coordinate method was done on the "opt=redundant" optimized chair transition structure (using 50 points along the IRC). The last point on the IRC was optimised using the HF/3-21G level of theory. The last point on the IRC (before optimisation) has a total energy of -231.69158 a.u.; the optimised form of this structure has a total energy of 231.69167 a.u. - this corresponds to the gauche2 conformer.

Summary table

Summary	Results
File name	optimisation_42_gauche2
File type	.fch
Calculation Type	FOPT
Calculation Method	RHF
Basis set	3-21G
Charge	0
Spin	Singlet
E(RHF)	-231.69167 a.u.
RMS Gradient Norm	0.00000 a.u.
Imaginary Freq	1
Dipole moment	0.38 Debye
Point Group	C₂

This is the unsuccessfully optimised job file: IRC_chair.

This is the successfully optimised job file: 42_chair.

Optimisation of the chair and boat transitions structures using the B3LYP/6-31G* level of theory

Boat

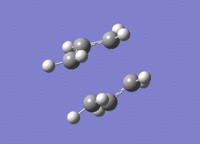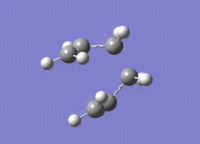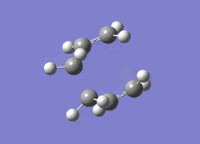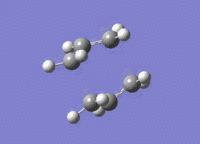
The structure of the boat transition state is the same as what it was using the previous level of theory (point group is still C_2v). The energy of the new transition state structure is -234.54309 a.u.; the structure is a transition state because the structure only has one imaginary vibrational mode at (-)530 cm^-1.

The difference in total energy between the reactants (two Hart-tree optimised allyl fragments) and the boat Hart-tree optimised transition state is (-)0.04328 a.u.; the energy of the individual allyl fragments is -115.82304 a.u..

The difference in total energy between the reactants (two DFT optimised allyl fragments) and the boat DFT optimised transition state is (+)0.02239 a.u.; the energy of the individual allyl fragments is -117.26035 a.u..

Summary table

Summary	Results
File name	BOAT_B3LYP6-31G_OPTIMISATION
File type	.log
Calculation Type	FTS
Calculation Method	RB3LYP
Basis set	6-31G(d)
Charge	0
Spin	Singlet
E(RB3LYP)	-234.54309 a.u.
RMS Gradient Norm	0.00000 a.u.
Imaginary Freq	1
Dipole moment	0.06 Debye
Point Group	C_2v

opt_boat and freq_boat.

Item table

Item                       Value      Threshold   Converged?
 Maximum Force            0.000009     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000141     0.001800     YES
 RMS     Displacement     0.000045     0.001200     YES
 Predicted change in Energy=-2.565747D-09
 Optimization completed.
    -- Stationary point found.

Low frequencies

Low frequencies --- -530.3604   -8.4039   -0.0002    0.0008    0.0012   15.4620
Low frequencies ---   17.6139  135.6118  261.6999

Summary of energies

B3LYP/6-31G*
	Electronic energy (a.u.)	zero-point energy (a.u.)	Sum of electronic and zero-point energies (a.u.)	Sum of electronic and zero-point energies (KCalmol^-1)	Thermal energy (a.u.)	Sum of electronic and thermal energies (a.u.)	Sum of electronic and thermal energies (KCalmol^-1)
		at 0 K	at 0 K	at 0 K	at 298.15 K	at 298.15 K	at 298.15 K
Boat TS	-234.54309	0.12567	-234.41742	-1.47099 x10⁵	0.13265	-234.41044	-1.47095 x10⁵
*Reactant (anti2)*	-234.61171	0.12724	-234.48447	-1.47141 x10⁵	0.13517	-234.47654	-1.47136 x10⁵

The activation energy at 0 K is the difference between the "sum of electronic and zero-point energies" for the boat transition state and the anti2 conformer. From the tabulated results above, the activation energy is 42 KCalmol^-1. Similarly, the activation energy at 298.15 K is the difference between the "sum of electronic and thermal energies" for the boat transition state and the anti2 conformer. From the tabulated results above, the activation energy is 41 KCalmol^-1. The activation energy calculated at 0 K gives us a result that is slightly closer to the experimental value of 44.7 ± 2.0 KCalmol^-1 (at 0 K).

Chair

The structure of the chair transition structure is the same as what it was using the previous level of theory (point group is still C_2h). The energy of the new transition state structure is -234.55698 a.u.; this structure is a transition state because it only has one imaginary vibrational mode at (-)566 cm^-1.

The difference in total energy between the reactants (two Hart-tree optimised allyl fragments) and the chair Hart-tree optimised transition state is (+)0.02676 a.u.; the energy of the individual allyl fragments is -115.82304 a.u..

The difference in total energy between the reactants (two DFT optimised allyl fragments) and the chair DFT optimised transition state is (+)0.03628 a.u.; the energy of the individual allyl fragments is -117.26035 a.u..

Summary table

Summary	Results
File name	CHAIR_TS_ALLYL_631GD
File type	.log
Calculation Type	FTS
Calculation Method	RB3LYP
Basis set	6-31G(d)
Charge	0
Spin	Singlet
E(RB3LYP)	-234.55698 a.u.
RMS Gradient Norm	0.00003 a.u.
Imaginary Freq	1
Dipole moment	0.00 Debye
Point Group	C_2h

opt_chair and freq_chair.

Item table

Item               Value     Threshold  Converged?
 Maximum Force            0.000053     0.000450     YES
 RMS     Force            0.000011     0.000300     YES
 Maximum Displacement     0.000988     0.001800     YES
 RMS     Displacement     0.000246     0.001200     YES
 Predicted change in Energy=-5.051083D-08
 Optimization completed.
    -- Stationary point found.

Low frequencies

 Low frequencies ---  -18.3528  -14.6266  -11.5337    0.0006    0.0008    0.0009
 Low frequencies ---   63.3097   97.1475  103.5644

Summary of energies

B3LYP/6-31G*
	Electronic energy (a.u.)	zero-point energy (a.u.)	Sum of electronic and zero-point energies (a.u.)	Sum of electronic and zero-point energies (KCalmol^-1)	Thermal energy (a.u.)	Sum of electronic and thermal energies (a.u.)	Sum of electronic and thermal energies (KCalmol^-1)
		at 0 K	at 0 K	at 0 K	at 298.15 K	at 298.15 K	at 298.15 K
Chair TS	-234.55698	0.12683	-234.43015	-1.47107 x10⁵	0.13338	-234.42360	-1.47103 x10⁵
*Reactant (anti2)*	-234.61171	0.12724	-234.48447	-1.47141 x10⁵	0.13517	-234.47654	-1.47136 x10⁵

The activation energy at 0 K is the difference between the "sum of electronic and zero-point energies" for the chair transition state and the anti2 conformer. From the tabulated results above, the activation energy is 34 KCalmol^-1. Similarly, the activation energy at 298.15 K is the difference between the "sum of electronic and thermal energies" for the chair transition state and the anti2 conformer. From the tabulated results above, the activation energy is 33 KCalmol^-1. The activation energies that were calculated at 0 K and 298.15 K are both equally as close to the experimental value of 33.5 ± 0.5 KCalmol^-1 (at 0 K) - and they are both within the region of uncertainty.

Final comments about the tutorial

No problems were encountered whilst undertaking this tutorial.

The Diels Alder Cycloaddition

1,3-Butadiene

HOMO and LUMO

Molecular Orbital	Diagram	Bonding or Antibonding?	Energy (a.u.)	Symmetry
HOMO		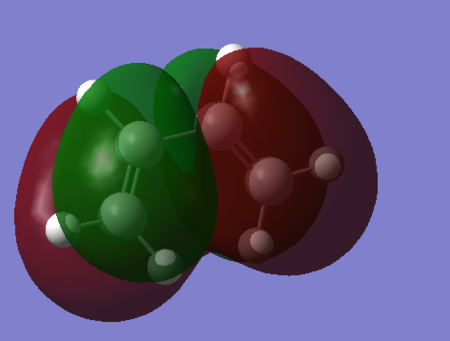Bonding.	-0.35322.	Symmetric.
LUMO		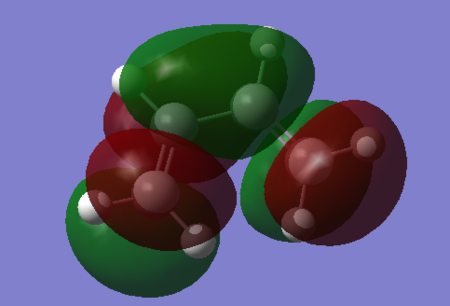Antibonding.	0.01136.	Antiymmetric.

Summary table

Summary	Results
File name	BUTADIENE_OPTIMISATION
File type	.log
Calculation Type	FOPT
Calculation Method	RPDDG
Basis set	ZDO
Charge	0
Spin	Singlet
E(RPDDG)	0.04591539 a.u.
RMS Gradient Norm	0.00003 a.u.
Imaginary Freq
Dipole moment	0.06 Debye
Point Group	C₂

opt_butadiene

Cyclohexene

HOMO and LUMO of the transition state

Molecular Orbital	Diagram	Bonding or Antibonding?	Energy (a.u.)	Symmetry
HOMO		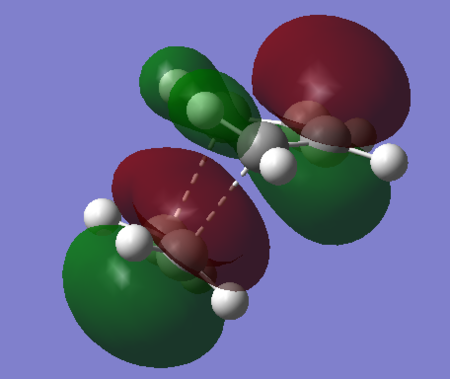Bonding.	-0.21896.	Symmetric.
LUMO		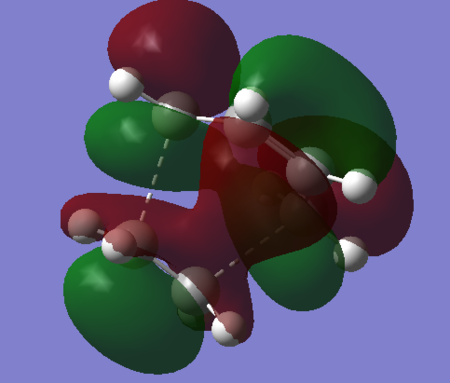Antibonding.	-0.00861.	Symmetric.

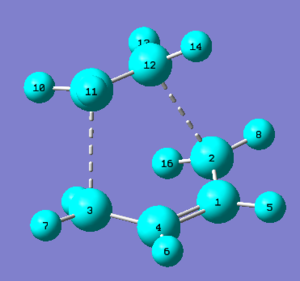
Structure

Summary	Results
File name	CYCLOHEXENE_OPTIMISATION_frequency
File type	.fch
Calculation Type	FOPT
Calculation Method	RB3LYP
Basis set	6-31G(d)
Charge	0
Spin	Singlet
E(RB3LYP)	-234.54390 a.u.
RMS Gradient Norm	0.00002 a.u.
Imaginary Freq	1
Dipole moment	0.39 Debye
Point Group

opt_freq_cyclohexene.

Bond lengths

Bond	Bond length (Å)	Hybridisation
C4-H6	1.08909.	sp² - H
C9-H11	1.08420.	sp³ - H
C9-H10	1.08628.	sp³ - H
C12-H11	1.08418.	sp³ - H
C12-H13	1.08628.	sp³ - H
C1-H5	1.08907.	sp² - H
C3-H7	1.08731.	sp^2.5 - H
C3-H15	1.08404..	sp^2.5 - H
C2-H8	1.08732.	sp^2.5 - H
C2-H16	1.08404.	sp^2.5 - H
C4=C1.	1.40722.	sp² - sp²
C9-C12.	1.38598.	sp³ - sp³
C4-C3.	1.38307.	sp² - sp^2.5
C1-C2.	1.38313.	sp² - sp^2.5
C9-------C3.	2.27207	sp³ - sp^2.5
C12-------C2.	2.27235	sp³ - sp^2.5

The typical sp³ - sp³ C-C bond length is 1.54 Å; the typical sp³ - sp² C-C bond length is 1.50 Å; and the typical sp² - sp² C-C bond length is 1.47 Å.^[1] The Van der Waals radius of a C atom is 1.70 Å.^[2] A covalent radius (twice the distance of a covalent bond) is generally smaller than the Van der Waals radius because the Van der waals radius is double the distance of closest approach between two non-bonded atoms (of the same element) that are merely colliding with one another without reacting to form a bond. This is the reason why the bond length of the partly formed σ C-C bonds in the transition state of cyclohexene is smaller than 3.4 Å.

Vibration

The formation of the two new bonds is synchronous. The vibration that corresponds to the reaction path at the transition state is a stretching vibrational mode, whereas the lowest positive frequency is a twisting vibrational mode; ethylene and s-cis butadiene vibrate as if they are already a single molecule in the lowest positive vibrational mode, whereas ethylene and s-cis butadiene vibrate as if they are separate molecules in the vibrational modes that corresponds to the reaction path at the transition state.

Low frequencies

 Low frequencies --- -525.1800 -5.3446 -0.0007 -0.0006 -0.0004 10.9440
Low frequencies --- 20.0558 135.8245 203.7598

Item table

Item                  Value         Threshold        Converged?
Maximum Force        0.000057        0.000450           YES
RMS Force            0.000009        0.000300           YES
Maximum Displacement 0.001795        0.001800           YES
RMS Displacement     0.000504        0.001200           YES
Predicted change in Energy=-4.090426D-08
Optimization completed.
-- Stationary point found.

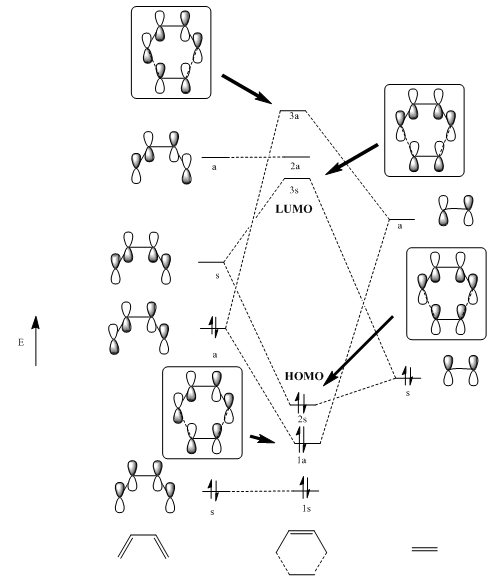
MO diagram

The reaction is allowed because, as illustrated on the MO diagram above, the HOMO of ethylene can interact with the LUMO of 1,3-Butadiene and the HOMO of 1,3-Butadiene can interact with the LUMO ethylene. Also, the electrons of the cyclohexene transition state are only occupying bonding (or non-bonding) MOs; the transition state is stabilised because no electron is occupying an antibonding MO.

Stereoselectivity of the Diels Alder Reaction

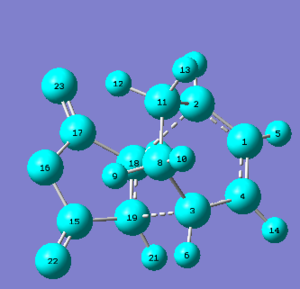
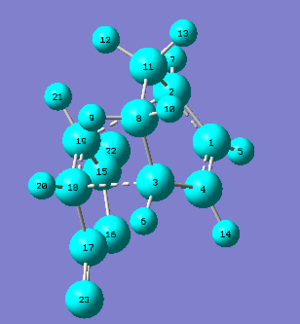
The exo Diels-Alder transition state adduct has a total energy of -612.67931 a.u., whileas the endo Diels-Alder transition state adduct has a total energy of -612.68340 a.u. - this means that the endo Diels-Alder product is the kinetic product. The C=O bonds of maleic anhydride are pointing in the direction of cyclo-1,3-hexadiene's pi-system in the endo transtion state, whileas the C=O bonds of maleic anhydride are pointing away from cyclo-1,3-hexadiene's pi-system in the exo transition state.

The exo transition state is less sterically strained because the substituents from maleic anhydride (the dienophile) is pointing towards the smaller bridge (and is pointing away from the larger bridge); the reason why the endo transitiion state is more sterically strained is because the substituents from the dienophile is pointing towards the larger bridge (and is pointing away from the smaller bridge).

The structures that are shown on the left are the transition structures for the Diels-Alder reaction because both structures only have one imaginary frequency mode.

HOMO and LUMO of the endo transition state

Molecular Orbital	Diagram	Energy (a.u.)	Symmetry
HOMO		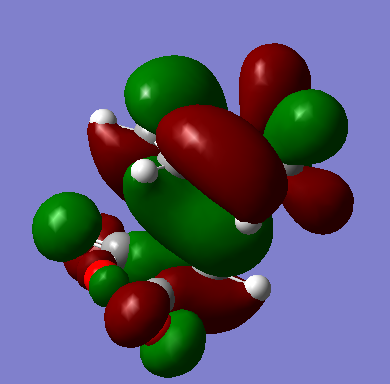-0.24230.	Antisymmetric.
LUMO		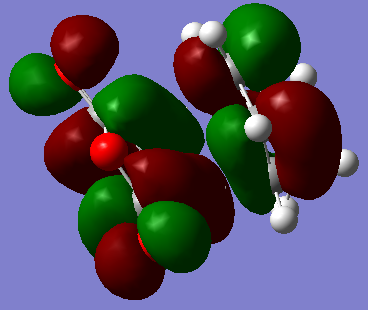-0.06773.	Antisymmetric.

Summary table

Summary	Results
File name	ENDO_DIELS_ALDER
File type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis set	6-31G(d)
Charge	0
Spin	Singlet
E(RB3LYP)	-612.68340 a.u.
RMS Gradient Norm	0.000008 a.u.
Imaginary Freq	1
Dipole moment	6.11 Debye
Point Group	C₁

opt_freq_endo.

Item table

Item                        Value     Threshold   Converged?
 Maximum Force            0.000023     0.000450     YES
 RMS     Force            0.000003     0.000300     YES
 Maximum Displacement     0.000455     0.001800     YES
 RMS     Displacement     0.000122     0.001200     YES
 Predicted change in Energy=-5.350598D-09
 Optimization completed.
    -- Stationary point found.

Low frequencies

Low frequencies --- -447.0370  -14.2013   -0.0007    0.0003    0.0004    4.6897
Low frequencies ---   11.2730   59.6773  118.3724

HOMO and LUMO of the exo transition state

Molecular Orbital	Diagram	Energy (a.u.)	Symmetry
HOMO		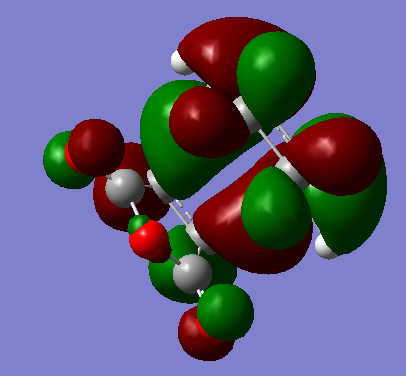-0.24215.	Antisymmetric.
LUMO		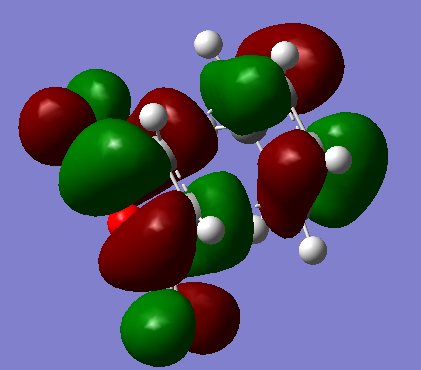-0.07842.	Antisymmetric.

Summary table

Summary	Results
File name	EXO_DIELS_ALDER
File type	.log
Calculation Type	FREQ
Calculation Method	RB3LYP
Basis set	6-31G(d)
Charge	0
Spin	Singlet
E(RB3LYP)	-612.679311 a.u.
RMS Gradient Norm	0.00002 a.u.
Imaginary Freq	1
Dipole moment	5.55 Debye
Point Group	C₁

opt_freq_exo.

Item table


 Item                     Value        Threshold  Converged?
 Maximum Force            0.000076     0.000450     YES
 RMS     Force            0.000009     0.000300     YES
 Maximum Displacement     0.001334     0.001800     YES
 RMS     Displacement     0.000367     0.001200     YES
 Predicted change in Energy=-1.689065D-08
 Optimization completed.
    -- Stationary point found

Low frequencies

 Low frequencies --- -448.2368  -13.9880  -11.9194    0.0002    0.0008    0.0010
 Low frequencies ---    3.1396   53.2571  109.0993

Bond lengths

Bond lengths for the exo adduct

Bond	Bond length (Å)	Hybridisation
C3-C8	1.51466.	sp^2.5 - sp³
C8-C11	1.55838.	sp³ - sp²
C11-C2	1.51451.	sp³ - sp^2.5
C19-C15	1.47939.	sp³ - sp²
C18-C17	1.47945.	sp³ - sp²
C1===C4	1.40352.	sp² - sp²
C4===C3	1.39138.	sp² - sp^2.5
C1===C2	1.39133.	sp² - sp^2.5
C19===C18	1.39785.	sp^2.5 - sp^2.5
C19-----C3	2.29117.	sp^2.5 - sp^2.5
C18-----C2	2.29056.	sp^2.5 - sp^2.5

The C-C through space distances between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the C atoms of the “opposite” -CH2-CH2- for the exo transition state is between 3.02801 (C17 and C11) - 3.02813 (C15-C8) Å.

Bond lengths for the endo adduct

Bond	Bond length (Å)	Hybridisation
C3-C8	1.51511.	sp^2.5 - sp³
C8-C11	1.55824.	sp³ - sp²
C11-C2	1.51507.	sp³ - sp^2.5
C19-C15	1.47948.	sp³ - sp²
C18-C17	1.47951.	sp³ - sp²
C1===C4	1.40307.	sp² - sp²
C4===C3	1.39125.	sp² - sp^2.5
C1===C2	1.39124.	sp² - sp^2.5
C19===C18	1.39398.	sp^2.5 - sp^2.5
C19-----C2	2.26837.	sp^2.5 - sp^2.5
C18-----C3	2.26829.	sp^2.5 - sp^2.5

The C-C through space distances between the -(C=O)-O-(C=O)- fragment of the maleic anhydride and the “opposite” -CH=CH- fragment for the endo transition state is 2.99007 Å.

Secondary orbital interactions

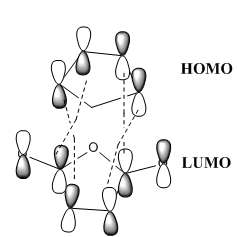
This is the secondary overlap orbital overlap effect that is present in the endo transition state.^[3]

The exo transition state is the thermodynamically favoured transition state because, as mentioned earlier, the exo transitiion state is less sterically strained. The endo transition state is the kinetically favoured transition state because of the so called “secondary orbital overlap effect”. As mentioned previously, the C=O bonds of maleic anhydride are pointing in the direction of cyclo-1,3-hexadiene's pi-system in the endo transtion state. The HOMO of cyclo-1,3-hexadiene is able to overlap with the LUMO of maleic anhydride - this lowers the energy of the transition state relative to that of the exo transition state; this interaction is not present in the exo transition state because the C=O bonds of maleic anhydride are pointing away from cyclo-1,3-hexadiene's pi-system.

The HOMO of the endo transition state has four strong σ bonding interactions between the p orbitals of the -(C=O)-O-(C=O)- fragment and the p orbitals from cyclo-1,3-hexadiene; the HOMO has four nodes in total. The HOMO of the exo transition state, on the other hand, has four strong σ antibonding interactions between the p orbitals of the -(C=O)-O-(C=O)- fragment and the p orbitals from cyclo-1,3-hexadiene; the HOMO has eight nodes in total.

In conclusion, the secondary orbital overlap effect helps to stabilise the endo transition state, this is not the case for the exo transition state; the strong σ antibonding interactions destabilise the exo transition state, relative to the endo transition state.

Further comments

Electronic effects (the secondary overlap orbital effect), steric effects, stereospecificity effects (the idea that the stereochemistry of the dienophile is always maintained because the diene undergoes a syn addition to the dienophile), and stereoselectivity (the endo being the favoured product) were all included in the calculations of the Diels-Alder transition states. The effect of electron donating groups on the diene facilitate reaction (regioselectivity) was neglected because both ethylene doesn't have any electron withdrawing substituents - such as a carbonyl group, an amine group etc., and maleic anhydride has two carbonyl groups, but the carbonyl groups are both the same distance away from the double bond (maleic anhydride is symmetric, with respect to the double dond). Also, 1,3-butadiene and cyclo-1,3-hexadiene don't have any electron releasing substituents. The regioselectivity effect is based upon the idea that the carbon (of the dienophile) that bears the most electron withdrawing substituent will bond to the carbon (of the diene) that bears the most electron releasing substituent, and vise versa.

The question of whether Diels-Alder reactions using a more electron rich version of the same diene can give lower or higher activation energies (and how do these transition structures vary, with respect to each other), when reacted with the same dienophile, was neglected. Similarly, The question of whether Diels-Alder reactions using a more electron poor version of the same dienophile can give lower or higher activation energies (and how do these transition structures vary, with respect to each other), when reacted with the same diene, was also neglected.

In conclusion, the results that were derived from this experiment can be explained using various theories within physical and organic chemistry.

References

↑ http://pubs.rsc.org/en/content/articlepdf/1987/p2/p298700000s1 F.H. Allen et al., Tables of bond lengths determined by X-ray and neutron diffraction. Part 1. Bond lengths in organic compounds, J. CHEM. SOC, 1987, 1-19.
↑ Rowland RS, Taylor R (1996). "Intermolecular nonbonded contact distances in organic crystal structures: comparison with distances expected from van der Waals radii". J. Phys. Chem. 100 (18): 7384–7391. doi:10.1021/jp953141
↑ Ian Fleming (1976), "Frontier Orbitals and Organic Chemical Reactions", Wiley-Blackwell, 120 - 160.

[1] ttp://pubs.rsc.org/en/content/articlepdf/1987/p2/p298700000s1 F.H. Allen et al., Tables of bond lengths determined by X-ray and neutron diffraction. Part 1. Bond lengths in organic compounds, J. CHEM. SOC, 1987, 1-19.

[2] Rowland RS, Taylor R (1996). "Intermolecular nonbonded contact distances in organic crystal structures: comparison with distances expected from van der Waals radii". J. Phys. Chem. 100 (18): 7384–7391. doi:10.1021/jp953141

[3] Ian Fleming (1976), "Frontier Orbitals and Organic Chemical Reactions", Wiley-Blackwell, 120 - 160.

[1]

[2]

[3]