The Cope Rearrangement Tutorial

Introduction

Developed in the 1940s by Arthur C. Cope ^[1], the Cope rearrangement is a pericyclic transformation involving a [3,3]-sigmatropic rearrangement of 1,5 dienes. Its mechanism has been intensely studied both experimentally and computationally; it is now accepted that a concerted mechanism (depicted below for 1,5-hexadiene) operates via either a "chair" or a "boat" transition structure.

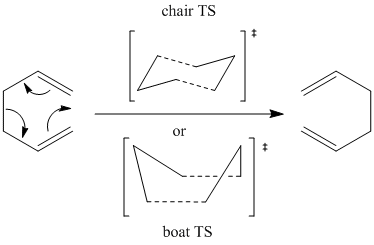
Mechanism for the Cope rearrangement of 1,5-hexadiene

The aim of this section is to use computational methods to investigate the low-energy minima and transition structures of the Cope rearrangement in order to establish the preferred reaction mechanism.

Optimizing the Reactants and Products

**HF/3-21G level of theory optimizations results**
	Conformation 1 (Anti 2)	Conformation 2 (Gauche 3)
Total energy / a.u.	-231.69253528	-231.69266122
RMS Gradient Norm / a.u.	0.00001896	0.00000704
Dipole moment / Debye	0.0000	0.3405
Point group	C_i	C₁
Relative energy / kcal mol^-1	0.08	0.00
Structure

1,5-hexadiene was drawn in GaussView using the builder. The structure was cleaned up, then the dihedral angle was set to 180^o, making the linkage between the central four C atoms "anti" (approximately antiperiplanar conformation) to generate conformation 1.
To generate conformation 2, the dihedral angle was set to 60^o to make the linkage between the central four C atoms "gauche".
The structures were optimized at the less accurate HF/3-21G level of theory in order to find the lowest energy state and optimize it further more accurately. An "Optimization" job was submitted in Gaussian under the Calculate menu (method: Hartree Fock, basis set: 3-21G). The calculations were repeated until obtaining convergence for both force and displacement. By inspecting the checkpoint file and the symmetry of the structures, the results summarized in the table on the right were found.

Output for Anti 2 optimization: (actual file uploaded here)

Item               Value     Threshold  Converged?
Maximum Force            0.000060     0.000450     YES
RMS     Force            0.000010     0.000300     YES
Maximum Displacement     0.000316     0.001800     YES
RMS     Displacement     0.000099     0.001200     YES
Predicted change in Energy=-1.847600D-08
Optimization completed.
   -- Stationary point found.

Output for Gauche 3 optimization: (actual file uploaded here)

        Item               Value     Threshold  Converged?
Maximum Force            0.000011     0.000450     YES
RMS     Force            0.000004     0.000300     YES
Maximum Displacement     0.000998     0.001800     YES
RMS     Displacement     0.000428     0.001200     YES
Predicted change in Energy=-1.196095D-08
Optimization completed.
   -- Stationary point found.

The energies obtained were compared to those shown in Appendix 1 of the lab script; these matched the energies of conformers Anti2 and Gauche3.

The orientation of the bonds was modified to generate the 8 other energetically distinct conformers shown in Appendix 1. All conformers required 2 optimizations, apart from Gauche 5 and Gauche 6, which needed 4, respectively 3 optimizations in order to reach convergence for both force and displacement. The table below summarizes these findings (click on the links for jmol structures).

**Other possible conformers**
	Gauche	Gauche 2	Gauche 4	Gauche 5	Gauche 6	Anti 1	Anti 3	Anti 4
Total energy / a.u.	-231.68771617	-231.69166702	-231.69153032	-231.68961576	-231.68916020	-231.69260236	-231.68907067	-231.69097057
RMS Gradient Norm / a.u.	0.00000543	0.00000303	0.00001871	0.00000323	0.00000328	0.00001297	0.00000301	0.00000229
Dipole moment / Debye	0.4557	0.3804	0.1281	0.4438	0.5361	0.2021	0.0001	0.2955
Point group	C₂	C₂	C₂	C₁	C₁	C₂	C_2h	C₁
Relative energy / kcal mol^-1	3.10	0.62	0.71	1.91	2.20	0.04	2.25	1.06
Actual output file	Here	Here	Here	Here	Here	Here	Here	Here
Structure

The average energy of the gauche conformers is 1.42 kcal mol^-1, higher than the average energy of the anti conformers, which is 0.86 kcal mol^-1. This is not surprising: in the gauche conformation, the two vinyl groups are 60^o apart, creating more steric clash than in the anti conformation, with 180^o distance and stabilizing hyperconjugation in operation.

The most stable conformer adopts, however, a gauche geometry, namely Gauche 3. Examination of the geometry of the structure reveals the close proximity of the double bonds, allowing a secondary orbital interaction between the π clouds of the two alkenes, providing additional stabilization to this conformer. The MOs of the structure were computed (Edit -> MOs -> visualize); the computed HOMO presents a favourable anterafacial overlap between the pi clouds of the two double bonds.
The Anti 2 conformation previously optimized at the HF/3-21G level of theory was re-optimized, this time using the DFT-B3LYP/6-31G* level of theory (by selecting DFT under the Method menu and the B3LYP function). The calculation succeeded after 2 optimizations:

        Item               Value     Threshold  Converged?
Maximum Force            0.000230     0.000450     YES
RMS     Force            0.000069     0.000300     YES
Maximum Displacement     0.001188     0.001800     YES
RMS     Displacement     0.000471     0.001200     YES
Predicted change in Energy=-8.054644D-07
Optimization completed.
   -- Stationary point found.

The output file is uploaded Here.

**Results comparison**
	HF-3-21G	DFT-B3LYP/6-31G(d)
Total energy / a.u.	-231.69253528	-233.33633752

A frequency analysis (2nd derivative of the potential energy curve) has to be conducted in order to confirm that a minimum has indeed been found. All vibrational frequencies need to be real and positive to have a convex potential energy curve. A transition state appears as a negative frequency, but if more than one negative frequencies are present, then the optimization has failed.
Under the Job Type tab, "Frequency" was selected and a calculation was run on the B3LYP/6-31G* structure (at the same level of theory). The log file was inspected; "vibrations" was selected under the results menu, showing all the vibrational frequency modes. The log file produced can be accessed here.
Only positive frequencies were obtained, confirming that a minimum was indeed achieved.

Thermochemical data was also computed:

Sum of electronic and zero-point Energies=           -231.539540
Sum of electronic and thermal Energies=              -231.532566
Sum of electronic and thermal Enthalpies=            -231.531622
Sum of electronic and thermal Free Energies=         -231.570914

Optimizing the "Chair" and "Boat" transition structures

The "chair" and "boat" transition states for the Cope rearrangement consist of C3H5 allyl fragments of C2h and C2v symmetry placed at ~2.2 Å apart. These transition structures will be examined using different computational methods to determine the most likely transition state structure.

Chair optimization

An allyl fragment (CH2CHCH2)was drawn and optimized (HF/3-21G level of theory; file here). Two such optimized fragments were used to construct a chair like transition state, setting the distance between the termini to 2.2 Å. Manual optimization using two different methods (Freeze coordinate and Berny) was then undergone.

Transition state (Berny) method

**Berny optimization results**
Parameter	Value
Energy / a.u.	-231.619322
Imaginary frequency/ cm^-1	-817.91
Point group	C_2h
Allyl fragment separation / Å	2.20

A reasonable guess of the transition state geometry is operated on in this case. The force constant matrix (Hessian) is computed. A MolGroup was created and the optimized guess structure was pasted into the window. A Gaussian optimization was set up: Opt+Freq was selected, Optimization was changed to a TS (Berny), the force constants were chosen to be calculated Once and Opt=NoEigen was typed at the bottom of the box (to prevent the calculation from crashing if more than one imaginary frequency is detected). Two calculations were undergone to achieve convergence; output file here.
The imaginary frequency animation indicates the concerted mechanism of bond forming and bond breaking.

Optimized structure	Imaginary frequency animation

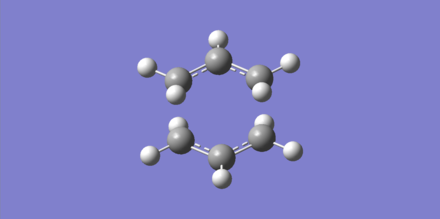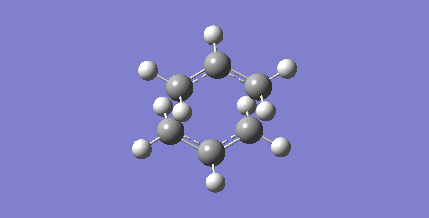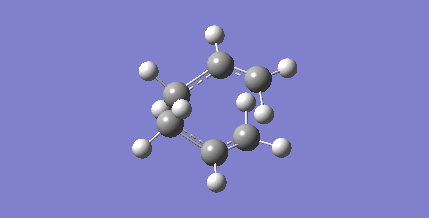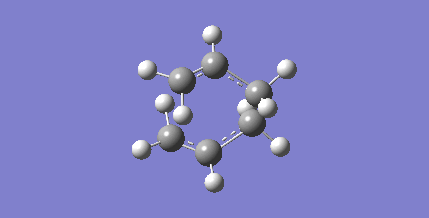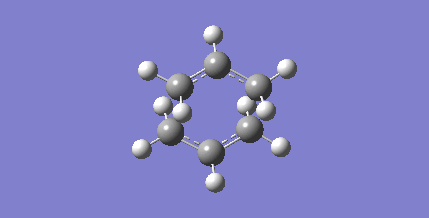Freeze coordinate method

The freeze coordinate method consists of freezing the reaction coordinate and minimizing the rest of the molecule. The guess structure was constructed and the Reduntant Coordinate Editor was selected from the Edit menu. "Bond" and "Freeze coordinate" were selected and the C termini pairs from the allyl fragments were selected. The optimization was set as if it was a minimum (keywords that appear: Opt=ModRedundant). The job was submitted, producing the following output:here.
When the job has finished, the chk file was opened. The bond breaking distances, fixed to 2.2 Å for the moment, were optimized. From the Redundant Coordinate Editor, the bonds that were previously frozen were selected; "bond" and "derivative" were selected. A transition state optimization was set up without calculating force constants (option = Never). Output file here.

Boat optimization

The QST2 method was used to optimize the boat transition structure. In this method, a transition state between the specified reactants and products is established. The reactants and products need to be numbered correctly in order for this to work, so manual numbering was performed.
Starting from the chk file of the optimized Ci reactant molecule (anti2), a MolGroup was created, 2 structures were copied and pasted, then manually edited from Atom List to establish a consistent numbering scheme.

Reactant	Product

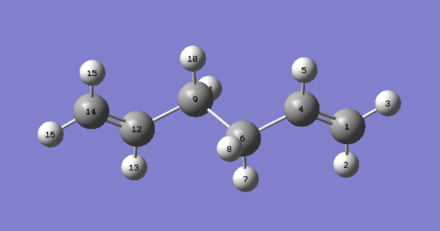A QST2 calculation was set up. An Opt+Freq job type was selected and optimization to a TS (QST2) set up. The job fails, producing a chair-like transition structure, but more dissociated. The possibility of rotation around the central bonds is not even considered. Manual editing is thus required. Log file here.

Gaussview procedure	Failed result

To edit the structures, the central C-C-C-C dihedral angles were changed to 0 and the inside C-C-C angles were reduced to 100 for both the reactant and product structure. A QST2 calculation was set up and the job was run again. Output file here. A boat transition structure was obtained, with an imaginary frequency at 840.28 cm-1. Therefore the QST2 method needs manually edited structure to produce a meaningful result.

Structures	Result

Intrinsic reaction coordinate method

It is impossible to predict which of the possible 10 conformers computed in the first section corresponds to the starting material leading to a certain transition state, hence the intrinsic reaction coordinate method can be employed to follow a minimum energy path from the transition structure down to its local minimum on a potential energy surface. A series of points (initially 50) is created by taking small geometry steps in the direction where the gradient or slope of the energy surface is steepest.

The Diels Alder Cycloaddition

Reaction Between Ethylene and Cis-Butadiene

The reaction between ethylene (dienophile) and cis-butadiene (diene) is one of the simplest Diels Alder cycloadditions. The AM1 semi-empirical molecular orbital method is used rather than Hartree-Fock and DFT.

Reactants optimization

Butadiene and ethylene were drawn and optimized (semiempirical, AM1; files: butadiene, ethylene). The HOMO and LUMO of each structure were inspected (Edit -> MOs, Visualize, Update). The HOMO of ethylene and LUMO of butadiene are both symmetric with respect to the reflection plane, while the HOMO of butadiene and LUMO of ethylene are antisymmetric. Therefore these pairs can interact.

Butadiene HOMO	Butadiene LUMO	Ethylene HOMO	Ethylene LUMO

AntiSymmetric	Symmetric	Symmetric	AntiSymmetric

Computation of the Transition State geometry

The transition state has an envelope type structure which maximizes orbital overlaps. First, the bicyclo system on the left was constructed by drawing a cyclohexane in the chair form, adding the double bond and the bridging -CH2-CH2- and using the clean function to clean up the structure. This structure was optimized (semiempirical, AM1) to produce this output. Two methylenes were deleted, the bonds to the bridge were removed and the distance between the termini was set to 2.2 Å. A minimization to a TS (Berny) was performed (force constant calculated once, additional keywords: opt=noeigen in case more than one imaginary frequency is detected). Output files: here, here. A transition state was indeed found, as confirmed by the imaginary frequency obtained at -956.21 cm-1.

Optimized structure	Imaginary frequency animation

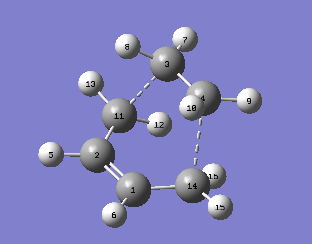**Transtion state optimization data**
Parameter	Value
Energy / a.u.	0.11165465
Imaginary frequency/ cm^-1	-956.21
C1-C14, C2-C11 bond length / Å	1.383
C1-C2 bond length / Å	1.397
C3-C4 bond length / Å	1.383
Fragment distance (C3-C11, C4-C14) / Å	2.119

The [4+2] cycloaddition (π4s + π2s, Hückel topology, suprafacial components) is allowed to proceed due to the possible interactions between the reactants (butadiene HOMO + ethylene LUMO, AS; butadiene LUMO + ethylene HOMO, S). The imaginary frequency animation illustrates the synchronous formation of two new sigma bonds, which is in agreement with the concerted nature of the mechanism of pericyclic reactions. The lowest positive frequency occurs at 147.27 cm-1 and corresponds to the asynchronous twisting of the fragments (animation here). The bond lengths give insight into the nature of the transition state; they are all close in value and intermediate between the length of a C-C single bond (1.54 Å) and a C=C double bond (1.34 Å); they are close to the length of a benzene bond (1.40 Å), which indicates the homo aromatic delocalized nature of transition state typical for pericyclic reactions. The distance between ethylene and butadiene is 2.119 Å, higher than a C-C single bond, but lower than the van der Waals radius of the carbons, which indicates that bonding is taking place.
The HOMO and LUMO of the transition state were computed; they are illustrated below.

HOMO	LUMO

AntiSymmetric	Symmetric

There is significant overlap between the pi clouds of the reactants, which supports the formation of new bonds.

Reaction Between Cyclohexa-1,3-diene and Maleic Anhydride

Cyclohexa-1,3-diene readily reacts with maleic anhydride as shown below. The transformation is stereospecific: only the endo product is formed. The reaction thus follows the endo rule, which states that the energy of the endo transition state is lower than for the exo isomer. Therefore under kinetic control, the endo isomer is most accessible and is formed first.

Reactants optimization

Cyclohexa-1,3-diene and Maleic Anhydride were drawn and optimized (semiempirical, AM1; files: cyclohexa-1,3-diene, maleic anhydride.The HOMO and LUMO of each structure were inspected (Edit -> MOs, Visualize, Update). The HOMO of cyclohexa-1,3-diene and LUMO of maleic anhydrideare both symmetric with respect to the reflection plane, while the HOMO of maleic anhydride and LUMO of cyclohexa-1,3-diene are antisymmetric.

Cyclohexa-1,3-diene HOMO	Cyclohexa-1,3-diene LUMO	Maleic Anhydride HOMO	Maleic Anhydride LUMO

AntiSymmetric	Symmetric	Symmetric	AntiSymmetric

Computation of the Transition State geometry

Two possible transition states exist, endo and exo.

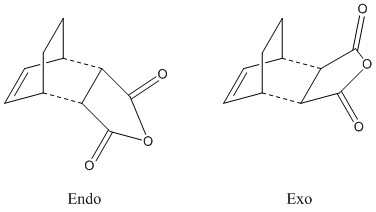
For both the endo and exo form, bicyclic structures were optimized first (semiempirical, AM1), then the new bonds were deleted, the distances were set to 2.2 Å and minimizations to a TS (Berny) were performed (force constant calculated once, additional keywords: opt=noeigen in case more than one imaginary frequency is detected).

Endo transition state

Output files: here, here.

Optimized structure	Imaginary frequency animation

The animation of the imaginary frequency (-806.43 cm-1) shows the concerted formation of the adduct, as expected.

HOMO	LUMO

Exo transition state

Output files: here, here.

Optimized structure	Imaginary frequency animation

The animation of the imaginary frequency (-812.21 cm-1) shows the concerted formation of the adduct, as expected.

HOMO	LUMO

Conclusion

Various computational methods have been used to localize transition states and prove the concerted nature of the mechanism of 3 pericyclic transformations (Cope rearrangement and two Diels-Alder reactions).

References

↑ Cope, A.C.; Hardy, E.M., J. Am. Chem. Soc. 1940, 62, 441.

[1] Cope, A.C.; Hardy, E.M., J. Am. Chem. Soc. 1940, 62, 441.

[1]