Rep:Mod:SJN2511

Simon Julien Nizard, S.A. RIdPEF

Hydrogenation of the Cyclopentadiene Dimer

The cyclopentadiene molecule is a popular compound in organometallic chemistry as a precursor to the cyclopentadienyl ligand, used in metallocene chemistry for its various hapticities. However, at room temperature, the colourless organic compound dimerizes to form dicyclopentadiene, via a Diels Alder cycloaddition (4 + 2) reaction, the scheme of which is shown below:

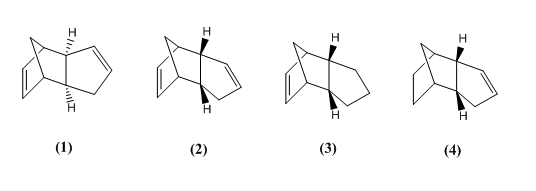
The preferred product is the endo- product, and as a first exercise, we shall endeavour to determine which isomer is the "lowest" in energy and attempt to rationalize the observations. The second part of the exercise shall consist of comparing the following 4 compounds: the endo (2) and exo (1) products, as well as the two monoene derivatives of the endo-dimer (3), (4).

To do so, the Chem3D program was used to analyse the molecules with molecular modelling. The molecules were sketched in the interface, and their energies were minimized using the MM2 force field calculation, which optimizes their geometries to an energy minimum and expressing the final energy as a sum of the bond length and angle strain, steric effects and van der Waals contributions. The results are shown in the table below:

MM2 minimization results on (1), (2), (3) and (4) (origins of energy contribution in kcal.mol^-1)

Compound	Stretch	Bend	Stretch-bend	Torsion	Non-1,4 v.d.Waals	1,4 v.d.Waals	Dipole/dipole	Total energy
(1)	1.29	20.58	-0.84	7.66	-1.42	4.23	0.38	31.88
(2)	1.25	20.85	-0.84	9.51	-1.54	4.32	0.45	34.00
(3)	1.28	19.86	-0.83	10.81	-1.22	5.63	0.16	35.69
(4)	1.09	14.52	-0.55	12.50	-1.07	4.51	0.14	31.15

Endo- vs exo- control

Exo dimer

Endo dimer

As can be seen from the results above, the most stable dimer is the exo-dimer, being more stable by 2.12 kcal.mol^-1 than the endo-product, mostly from torsional strain contribution. In the molecular representations on the left and right, the angles between the carbon bonds are highlighted to show the anti-periplanar conformation in (1) and a near-eclipsed conformation in (2) (in a loose sense analogous to chair and boat conformations of cyclohexane, the endo-dimer takes on a boat-like shape).

Since the endo-dimer is the known major product, it follows that the reaction occurs via kinetic control. Thus, the transition state of the endo-product is no doubt more stable/accessible than that of the exo-product, and the problem must be approached from an orbital theory angle, which is not covered by MM2 analysis.

Hydogenated endo-cyclopentadiene derivatives

In the hydrogenation of the endo-isomer of dicyclopentadiene, product (4) is less strained in the thermodynamic sense, by around 4.54 kcal.mol^-1, meaning it is easier to hydrogenate the double bond that is on the three-carbon bridge. The stretch and bend energies of (4) are lower, indicating less-strained bond angles (particularly on the sp₂ bonds). This makes sense, as the double bond closest to the bridge is the more strained, and is present in (3). Analysis of the angles shows 108° for the alkene bond in (3), and 113° for the alkene bond in (4). Normal sp₂ angles are usually 120°, which explains the greater strain in (3). Torsional strain is higher in (4) for similar reasons: the 3-carbon bridge/2-carbon bridge area is clearly the source of most of the torsion. Without the double bond there, the bridge attempts to to distort and causes strain on the more rigid part of the molecule. Van der Waals interactions are slightly higher in (3) by 1.12 kcal.mol_-1.

Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol

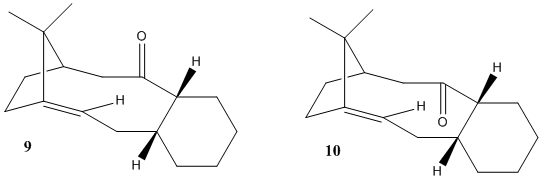
Taxol is an important cancer chemotherapy drug, isolated from the bark of the Pacific Yew Tree. Two possible conformations of a key intermediate of taxol are shown on the right, with the carbonyl group pointing either up or down. These are atropisomers, meaning that the demand for free rotation is too high and the molecules are "stuck" in one conformation or the other (energy minima). Working out which one is most stable will allow us to predict the stereochemistry at carbonyl. Our task will include sketching the molecules and minimizing their energy with molecular mechanics methods (MM2 and MMFF94 fields) as well as rationalizing the hyperstability of the bridgehead alkene bond that lies opposite the carbonyl.

The molecule was drawn with the cyclohexane ring in chair conformation to minimize the energy.

MM2 and MMFF94 energy calculations (Chem3D)

Compound 9 bond angles

Compound 10 bond angles

MM2 and MMFF94 minimization results on (9) and (10) (origins of energy contribution in kcal.mol^-1)

Compound	Stretch	Bend	Stretch-bend	Torsion	Non-1,4 v.d.Waals	1,4 v.d.Waals	Dipole/dipole	Total energy (MM2)	Total Energy (MMFF94)
(9)	2.78	16.54	0.43	18.25	-1.55	13.11	-1.72	47.84	70.53
(10)	2.57	13.44	0.31	17.67	-1.55	12.46	-1.59	43.31	61.04

The tabulated results above determine (consistent across both methods employed) that the "down" atropisomer (10) to be the most thermodynamically stable. This is in accordance with what the literature has reported: the "up" conformer (9) is less energetically favourable on account of inducing a higher-energy twist-boat conformation on the adjacent cyclohexane ring. Note that minimizing the energy of (9) was rendered difficult as a result, and required several minutes of tweaking in Chem3D to reduce it to a chair conformation.

The main part of the energy difference seems to stem from bend energy (3.10 kcal.mol^-1), which may be due to strain on the carbonyl sp₂ carbon: even assuming ideal C-C_carbonyl-C bond angle of 120° (it's usually a bit less), compound (9) exhibits 126°, compared to 120° for compound (10).

Rationalizing the hyperstability of the olefinic bridgehead

By running a comparative calculation on the saturated hydrocarbon derivative of compound 10 and compound 10 itself, we should be able to determine the olefinic strain energy as the total energy of the olefin minus the total energy of the saturated derivative. Below are the results of MM2 and MMFF94 optimizations of such a molecule.

MM2 minimization results on (10a hydrogenated) at olefinic bridgehead (origins of energy contribution in kcal.mol^-1)

Compound	Stretch	Bend	Stretch-bend	Torsion	Non-1,4 v.d.Waals	1,4 v.d.Waals	Dipole/dipole	Total energy (MM2)
(10a)	2.70	13.76	0.60	23.36	-2.68	16.89	-1.74	52.90

Compound 10a (saturated), bond angles and van der Waals distances

Note: the saturated derivative cyclohexane ring proved impossible to fit into a chair conformation, always twisting out into twist-boat conformation.

Thus, the olefinic strain for molecule 10 is 43.31 - 52.90 = -9.59 kcal.mol^-1. This is a negative value, meaning that the alkene is in fact more stable than the saturated compound, and would react very slowly with an electrophile. Overall, the sources of new energy in the saturated derivative are from torsion and van der Waals repulsion. The two go hand in hand: as the bridgehead alkene is saturated, the bridge takes on most of the added torsional strain, as can be seen on the diagram on the right, where sp₃ bond angles differ greatly from ideal 109.5°. In turn, the added torsion brings hydrogen atoms beneath and above the ring closer together (2.1 Å, down from 2.4 Å), increasing van der Waals repulsion and contributing to the overall strain (including the two new hydrogen atoms which also contribute).

Modelling Using Semi-Empirical Molecular Orbital Theory - Regioselective addition of Dichlorocarbene

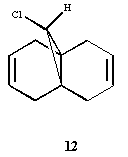
Consider the molecule on the left: 9-Chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene (12), which can undergo electrophilic attack from compounds such as dichlorocarbene. There are two potential sites for electrophilic attack, the two alkene bonds on either side of the bridge, and our task here is to determine which one is more favourable to electrophilic attack. As seen in the 1st chapter, molecular mechanics alone cannot handle analysis of "orbital control" of reactions. Thus, we shall use the MOPAC calculation method to determine the energy and geometries of molecular orbitals, particularly the HOMO, presumed to be the most reactive to electrophilic attack.

MOPAC/PM6 orbital calculations

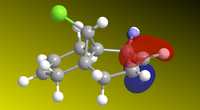
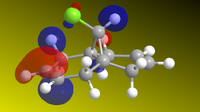
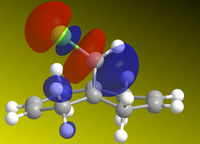
The molecule was sketched and roughly optimized using MM2 field, after which MOPAC/PM6methods were used to determine the HOMO-1, HOMO, LUMO, LUMO+1 and LUMO+2 and make them appear on the molecule. These are shown below. Heat of formation of 12 calculated to 19.74 kcal.mol^-1.

Calculated molecular orbitals for 9-Chloro-1,4,5,8-tetrahydro-4a,8a-methanonaphthalene (12)

HOMO-1	HOMO	LUMO	LUMO+1	LUMO+2

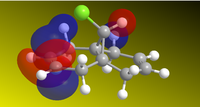From the HOMOs, we can see that HOMO-1 is located on the anti (or exo-) alkene bond (on the other side of the Cl), while the HOMO is located on the endo- alkene double bond, on the other side. This tells us that the endo-alkene is more nucleophilic (more open to electrophilic atack) by dichlorocarbene, as reported here. As if to further reinforce the point, the LUMO is located around the anti-alkene bond, meaning that this bond will more readily undergo nucleophilic attack instead of acting as an nucleophile. The LUMO+1 and LUMO+2 calculations serve to show that even the chlorine-carbon bond would undergo nucleophilic attack before the endo-alkene bond would.

12a derivative HOMO

Anti-monohydrogenated derivative of compound 12 and influence of the Cl-C bond on vibrational frequencies

The exo-hydrogenated (meaning the alkene bond anti- to the Chloride has been saturated) derivative 12a was subjected to MOPAC HOMO calculation to compare the heat of formation (-2.43110 kcal.mol^-1) with that of 12 and predict reactivity, as well as to analyze the influence of the Cl-C bond on the infrared vibrational spectrum. The first observation, purely from a HOMO point of view, is that it is not located on the alkene bond anymore, effectively lowering its reactivity.

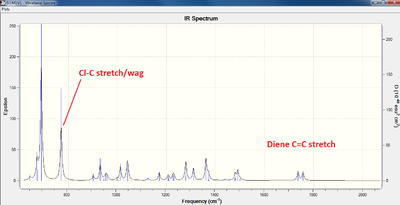
The molecules (12 and 12a) were analysed using the B3LYP/6-31G(d,p) Gaussian geometry optimization and frequency calculation, submitted to the SCAN machine. Below are the infrared spectra calculated for each molecule, as well as the relevant Cl-C and C=C stretching frequencies and their molecular representations: (data can be found here and here)

anti-alkene stretch (click to view)

endo-alkene stretch (click to view)

Cl-C stretch (click to view)

12 (diene)	12a (monoene)

Selected bond stretching frequencies

Bond type	12 (diene)	12a (monoene)
Cl-C stretch	770 cm-1	774 cm-1
endo- C=C stretch	1757 cm-1	1758 cm-1
exo- C=C stretch	1737 cm-1	n/a

From the diene results, it would appear that there is a correlation between the Cl-C bond's presence and the strength of the alkene bond: the exo-alkene bond is weaker as a result. This arises from the stabilising interaction of the σ*-Cl-C orbital on the exo-π-orbital which lowers the pi-bond's energy. Indeed, removal of the exo- bond by hydrogenation leads to a slight increase in energy of the Cl-C stretching frequency.

Monosaccharide Chemistry: Glycosidation

Neighbouring group participation

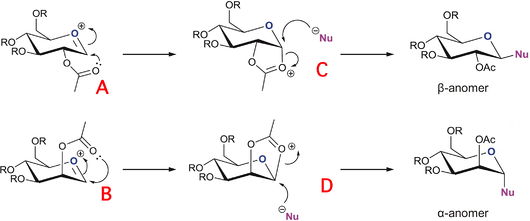
In the glycosidation of monosaccharides, the stereochemistry of the anomeric position (X on the diagrams) can be almost completely controlled by the "neighbouring group effect" from adjacent acetyl groups as outlined by the diagrams on the left. Depending on the position of the acetyl group (equatorial or axial), it attack on the bottom or top face (respectively), and generates the β- or α-anomer, respectively.

Our task to illustrate this diastereoisomery is to model the facial preferences, by using MOPAC/PM6 on top of MM2 field minimization and ascertaining which conformation is the most stable (thermodynamically). In our modelling, the 'R' groups used were Me (methyl) protecting groups, due to their conveniently small electron count and reduced propensity to hydrogen-bond to the rest of the molecule. This reduces computational load on the laptop, as well as reducing the margin for error (since the MOPAC calculations are only semi-empirical). The MM2 is clearly inferior for this job as it would not take into account electronic effects of the oxocarbenium and dioxolonium conjugated systems (the 5-membered or quasi-5-membered ring systems in the intermediates C and D)

MM2 and MOPAC/PM6 Results

Below are tables highlighting the energy difference between different conformers with both methods. Note that PM6 calculations automatically forced the protecting groups into "axial"-like positions.

PM6 and MM2 minimization results on conformers A-D (origins of energy contribution in kcal.mol^-1)

Compound	Comment	Stretch	Bend	Stretch-bend	Torsion	Non-1,4 v.d.Waals	1,4 v.d.Waals	Charge/Dipole	Dipole/dipole	Total energy [MM2]	Heat of Formation [PM6]
A	below plane	2.43	8.66	0.86	1.08	-3.34	18.79	0.31	5.06	33.85	-91.18
A`	slightly above plane	2.26	10.05	0.85	3.41	-2.63	19.63	-13.04	6.85	27.38	-85.75
B	above plane	2.37	10.46	0.87	1.32	-4.30	18.79	-1.20	4.43	32.75	-90.51
B`	slightly below plane	2.42	12.15	1.08	0.29	-2.33	16.81	11.77	5.40	47.58	-69.17
C	below plane	1.94	16.60	0.79	9.56	-2.09	17.27	-9.16	-1.31	33.59	-90.16
C`	slightly above plane	2.49	16.86	0.68	6.58	-2.89	19.31	2.04	-0.75	44.32	-66.88
D	above plane	2.01	13.52	0.70	7.45	-2.47	17.74	-10.47	-1.03	27.46	-91.66
D`	slightly below plane	2.51	19.02	0.60	4.30	-2.97	18.79	-1.51	-0.31	40.44	-59.16

Jmol images of conformers A-D

Method	A	A`	B	B`	C	C`	D	D`
MM2
PM6

As can be seen from the first table above, the main source of additional stability for A` (when compared to A) is in charge/dipole interaction between the polar carbonyl and the oxygen cation. This should have also been observed for B and B`, but somehow the value for the interaction energy came out positive. This charge/dipole interaction clearly serves to bring the acetyl group into a quasi-5-membered ring approach as the molecule moves from A to C/B to D.

For the intermediates C and D, they are much more stable than the strained C` and D`, it is apparent that the preferred conformation is with the dioxolenium ring causing as little strain on the sugar ring as possible, so as to afford the incoming nucleophile with the best angle of attack to form the anomer.

Mini-Project using DFT-based Molecular Orbital Methods: Stereoselective dissolving metal reductions

NOTE: DUE TO AN ERROR IN THE INITIAL SKETCHING OF THE MOLECULE, WHICH WENT UNDETECTED UNTIL FRIDAY, THE MOLECULE STUDIED IS SHORT OF ONE METHYL GROUP (IN BETWEEN THE RINGS). ALL DIAGRAMS AND CALCULATIONS IN THIS SECTION WERE CARRIED OUT ON THE ERRONEOUS MOLECULE

Introduction

In 1944, Birch reported the dissolving metal reduction of aromatic rings using sodium electride salt [Na(NH₃)_x]e⁻ and an alcohol. Unlike catalytic hydrogenation, this reaction hydrogenates only the 1,4 positions of a benzene ring, and electron directing substituents can influence the regiochemistry. In this report, we will analyse the reduction product of a cyclic ketone, which is reported to form an alcohol enantiomer. The reaction scheme and conditions are shown below :

We are interested in Step 2 in particular, and the characterisation of the alcohol (Structure 6 thereafter). A number of techniques can be employed to differentiate the ketone (Structure 5 thereafter) and 6. Infrared spectroscopy would pick up on the functional group difference between the two, and ¹H NMR spectroscopy would display an extra hydrogen shift. However, since the computational techniques used do not lend themselves to accurate prediction of ¹H NMR predictions, we shall confine ourselves to the ¹³C NMR spectrum calculation methods, and compare them with the literature. A brief molecular mechanics investigation will also be carried out using MM2 force-field on the two possible enantiomers of structure 6, as well as optical rotation calculations of the two, to be compared with the literature and discussed.

Vibrational spectrum calculation

The molecules (5 and 6) were analysed using the B3LYP/6-31G(d,p) Gaussian geometry optimization and frequency calculation, submitted to the SCAN machine. Below are the IR spectra obtained with significant differences highlighted. The stretching frequencies (calculated, corrected and compared with typical values are shown in the table below. Gaussian formatted checkpoint files can be found here and here. The correction factor used is that given in the module instructions (8%)

C=O stretch (click to view)

O-H stretch (click to view)

5 ketone	6 alcohol

Selected bond stretching frequencies

Compound	C=C stretch (calculated)	C=C stretch (corrected)	characteristic stretch	corrected value	typical frequency for FG
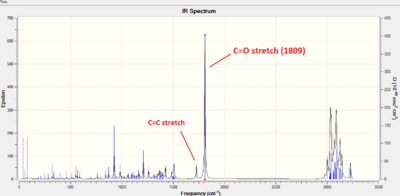
5 ketone	1725 cm-1	1594 cm-1	C=O 1809 cm-1	1675 cm-1	1700-1730 cm-1
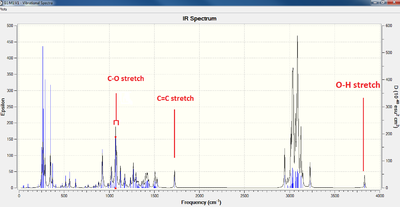
6 alchol	1725 cm-1	1594 cm-1	O-H 3832 cm-1	3548 cm-1	3200-3600

As is clearly indicated in the table above, differentiating the reagent from the starting material by infrared spectroscopy would be the simplest way of monitoring the progress of the ketone reduction. The C=O stretching peak is intense, making it easy to discern, and the O-H stretching peak, while not as intense, is isolated far upfield in the spectrum, making it also easily recognizable. The presence of the alkene bond in both products also indicates that the propylene group has not been reduced. IR does not, however, allow us to check if the reduction hasn't changed the structural integrity of the molecule - for this, a more in depth analysis is required, which brings us to ¹³C NMR.

¹³C and ¹H NMR spectroscopical calculations and analysis

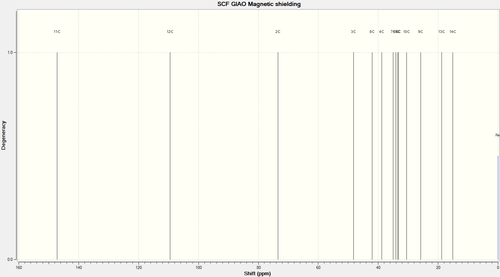
The geometries of molecules 5 and 6 were optimized using the DFT=MPW1PW91 method, and then submitted to the SCAN for NMR calculations [Basis set: 6-31G(d,p)]. Data for the these NMR calculations can be found here and here. Carbon numbering assigned automatically by Gaussview program:

5 ketone	6 alcohol

¹³C NMR calculated spectra and comparison with literature

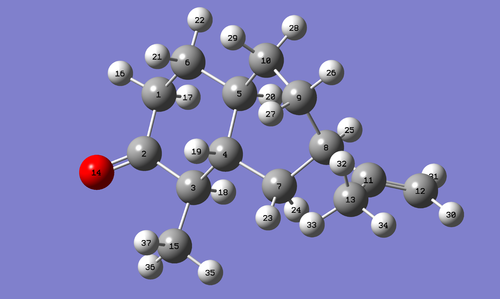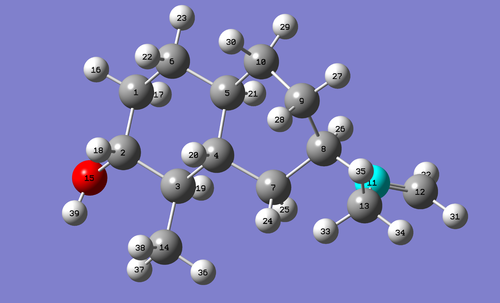Carbon number	Chemical Shift (ppm) Ketone (5)	Literature Value	Chemical Shift (ppm) Alcohol (6)	Literature value
C2	208.0 (corr: 212.7)	213.3	73.4	76.9
C11	146.7	146.3	147.2	147.1
C12	109.9	111.1	109.5	110.7
C3	52.2	45.66	48.2	43.2
C4	43.8	45.2	38.8	39.2
C8	42.2	41.7	42.0	39.9
C1	41.2	38.3	33.5	33.7
C7	37.1	38.2	35.0	38.9
C6	35.6	36.3	33.2	30.9
C5	33.6	34.0	34.2	37.1
C10	30.1	27.5	30.5	26.1
C9	25.8	23.0	25.8	23.1
C13	18.6	16.10	18.7	16.7
C14	13.6	11.18	15.1	14.9

The calculated NMR shifts for all carbons accord nicely with those reported in the literature. This would imply a conformationally stable molecule, especially for the alcohol product 6, where the stereochemistry of the OH group comes under scrutiny. A powerful tool for confirming which enantiomer would form would be by analysing the optical rotation of the product (see below). Another confirmation of the product conformation could come from predicting the 3JH-H couplings in Janocchio,, which uses the Karplus equation and a 3-D model of the molecule. Due to time constraint, this was not accomplished.

Optical Rotation

The DFT=MPW1PW91 optimized of the alcohol 6 and its , 6a, were input into the SCAN machine with the Cambridge variation of the B3LYP density functional method. The resulting optical rotations obtained were as follows (data: ) Structure 6: [α]₅₈₉ = 162°

Structure 6a: [α]₅₈₉ = 130°

This is way off the reported -11.6° value for the optical rotation, and might indicate the weakness of the conformational analysis method when more than 2 conformations are possible (as is often the case with 6-membered rings)

Molecular mechanics and investigation of the mechanism with semi-empirical MO methods

Proposed mechanism for the reduction of ketones by dissolved Lithium (M⁺)

Minimizing the energy and investigating the HOMO and LUMO of the 5 ketone structure could enable us to make a suggestion about the mechanism of reaction for the reduction of the ketone to the alcohol, as well as ascertaining which enantiomer would be formed

PM6 and MM2 minimization results on ketone 5 alcohol 6 and 6a (origins of energy contribution in kcal.mol^-1)

Compound	Stretch	Bend	Stretch-bend	Torsion	Non-1,4 v.d.Waals	1,4 v.d.Waals	Dipole/dipole	Total energy [MM2]	Heat of Formation [PM6]
5	1.46	3.15	0.28	10.94	-3.24	12.19	-1.66	23.13	-67.24
6	1.44	2.59	0.34	8.93	-3.78	12.39	0.01	21.94	-80.41
6a	1.43	2.82	0.36	9.90	-4.00	12.50	0.02	23.05	-81.20

Since the reaction is initiated by lone electrons solvated in the solutions, it stands to reason that the relevant orbital to look at is where the LUMO (most susceptible to nucleophilic attack) is located to begin rationalising a mechanism. The LUMO of ketone 5 was represented, as well as the relevant MOs of subsequent intermediate steps to propose a mechanism shown right (double e^- addition and double protonation).

Calculated molecular orbitals for initial ketone 5 and intermediates 1, 2 and 3

ketone LUMO	HOMO Intermediate 1	LUMO+1 intermediate 2	HOMO intermediate 3

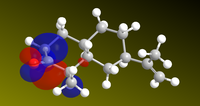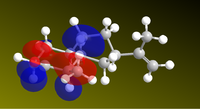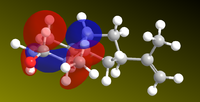Thus, the pi system around the carbonyl is the lowest unoccupied molecular orbital, which explains why the solvated electrons will perform nucleophilic attack on it rather than on the propenyl group. In intermediate 2, the LUMO+1 is a large orbital open to nucleophilic attack by a second electron. The calculations do not explain, however, why the HOMOs in intermediates 1 and 3 are located on the wrong atoms (they suggest that the oxygen is protonated before the carbon, which we know to be false. As a conclusion, this approach seems to be useful in rationalizing the sites of nucleophilic attack, but protonation is influenced by other forces in addition to those defined by molecular wave-functions.