Jump to content

Rep:Mod:HB9151

From ChemWiki

This is an exploration of molecules and reactions using GaussVeiw in order to understand the importance of computational inorganic chemistry.

Each molecule was draw in GaussVeiw and analysised computationally by solving the Schrödinger equation (EΦ=HΦ) under the Born-Oppenheimer approximation. Firstly the self-consistent field calculation is done for the starting bond lengths and angles giving the electronic wavefunction (Φ) that gives the lowest energy (for the fixed nuclei). The the distance is slightly shortened and the calculation repeated. This is continued until the lowest energy is found and this is the optimized structure. [1]

  1. ↑ http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year1/2_understand_opt_nh3.html

Once this structure is found the data given by the solutions can be used to explore many properties of the molecule such as the spectrum, molecular orbital and the overall energy of the molecule.


NH3

NH3

The optimisation file is liked to here

Proof of Structure Convergence


         Item               Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES
 Predicted change in Energy=-5.986294D-10
 Optimization completed.
    -- Stationary point found.


There is zero net force and displacement so the optimization has successfully converged and is complete.

Summary Information

NH3 Optimised Information
NH3
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
E(RB3LYP)/ au -56.55776873
RMS gradient / au 0.00000485
Point Group C3V
H-N bond length / A 1.01798
H-N-H bond angle / degrees 105.741

Molecule Vibrations


How many modes do you expect from the 3N-6 rule?

N represents the number of atoms in the molecule. For NH3 there are 4 molecules therefore; 3x4-6=6


Which modes are degenerate (ie have the same energy)?

Modes 2-3, and 5-6 are pairs of vibrations with the same energy (equal frequency).


Which modes are "bending" vibrations and which are "bond stretch" vibrations?

Modes 1-3 are bending and modes 4-6 are stretching. This is clear both from the animation and because bond stretching vibrations are higher in energy.



Which mode is highly symmetric?

Mode 4 is highly symmetric with no change in dipole.


One mode is known as the "umbrella" mode, which one is this?

Mode 1


How many bands would you expect to see in an experimental spectrum of gaseous ammonia?

There are four different vibrational energies suggesting four different bands. However there is only a minimal change in dipole for modes 4-6 so these would not be visible on a spectrum leaving only two bands.

Charge Distribution

Nitrogen has an electronegativity of 3.04 which is comparatively larger than hydrogen with 2.2. Therefore you would expect nitrogen to carry the negative charge. This is supported by the values calculated form the Schrödinger equation shown in the image below.


N2

N2


The optimisation file is liked to here

Proof of Structure Convergence


         Item               Value     Threshold  Converged?
 Maximum Force            0.000006     0.000450     YES
 RMS     Force            0.000006     0.000300     YES
 Maximum Displacement     0.000002     0.001800     YES
 RMS     Displacement     0.000003     0.001200     YES
 Predicted change in Energy=-1.248809D-11
 Optimization completed.
    -- Stationary point found.

There is zero net force and displacement so the optimization has successfully converged and is complete.

Summary Information

N2 Optimised Information
N2
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
E(RB3LYP)/ au -109.52412868
RMS gradient / au 0.00000365
Point Group D*H
N-N bond length / A 1.10550
N-N bond angle / degrees N/A

Molecule Vibrations

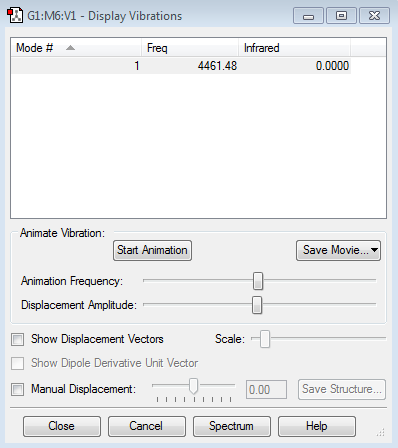
The 3N-5 rule used for linear molecules gives 3x2-5= 1. This is supported by the frequencies found from computational analysis as seen in the image above. This is due to the simple stretching of the bond.

Charge Distribution

Nitrogen has an electronegativity of 3.04. However when both atoms have the same electronegativity the charge is equally distributed across the molecule.


H2

H2


The optimisation file is liked to here

Proof of Structure Convergence


         Item               Value     Threshold  Converged?
 Maximum Force            0.000211     0.000450     YES
 RMS     Force            0.000211     0.000300     YES
 Maximum Displacement     0.000278     0.001800     YES
 RMS     Displacement     0.000393     0.001200     YES
 Predicted change in Energy=-5.852867D-08
 Optimization completed.
    -- Stationary point found.


There is zero net force and displacement so the optimization has successfully converged and is complete.

Summary Information

H2 Optimised Information
H2
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
E(RB3LYP)/ au -1.17853930
RMS gradient / au 0.00012170
Point Group D*H
H-H bond length / A 1.10550
H-H bond angle / degrees N/A

Molecule Vibrations

The 3N-5 rule used for linear molecules gives 3x2-5= 1. This is supported by the frequencies found from computational analysis as seen in the image above. This is due to the simple stretching of the bond.

Charge Distribution

Nitrogen has an electronegativity of 2.2. However when both atoms have the same electronegativity the charge is equally distributed across the molecule.


Haber-Bosch Process

Equation of Reaction

N2 + H2 -> NH3

Energy of Reaction

E(NH3)= -56.55776873 au

2*E(NH3)= 2*-56.55776873 = -113.1155375 au

E(N2)= -109.52412868 au

E(H2)= -1.17853930 au

3*E(H2)= 3*-1.17853930 = -3.5356179 au

ΔE = 2*E(NH3)-[E(N2)+3*E(H2)] = -113.1155375-[-109.52412868+-3.5356179]

ΔE = -0.05579092 au

ΔE = -0.05579092*2625.5 = -146.48 kJ/mol to 2.d.p


Stability of Reactants vs Products

ΔE is negative therefore the Haber process is exothermic and the product (NH3) is lower in energy and more stable than the reactants.


AlCl4-

AlCl4-

The optimisation file is liked to here

Proof of Structure Convergence


         Item               Value     Threshold  Converged?
 Maximum Force            0.000023     0.000450     YES
 RMS     Force            0.000014     0.000300     YES
 Maximum Displacement     0.000155     0.001800     YES
 RMS     Displacement     0.000093     0.001200     YES
 Predicted change in Energy=-7.051677D-09
 Optimization completed.
    -- Stationary point found.


There is zero net force and displacement so the optimization has successfully converged and is complete.

Summary Information

AlCl4- Optimised Information
AlCl4-
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
E(RB3LYP)/ au -2083.61641374
RMS gradient / au 0.00001174
Point Group TD
Al-Cl bond length / A 2.17703
Cl-Al-Cl bond angle / degrees 109.471

This is a much higher energy compound than that of N2 and H2.

Molecule Vibrations

The 3N-6 rule gives 3x5-6= 1. This is supported by the frequencies found from computational analysis as seen in the image above. Modes 7-9 are degenerate but in different directions. They are high energy due to the bending character creating a large change in dipole. Modes 3-5 are also degenerate bending vibrations but at a lower energy. Modes 1, 2 and 6 are all symmetrical vibrations that show no change in dipole and are therefore not visible on the spectrum as shown below.


Charge Distribution

Aluminum has an electronegativity of 1.61 which is comparatively smaller than that of chlorine with 3.16. Therefore you would expect aluminum to carry the positive charge. This is supported by the values calculated form the Schrödinger equation shown in the image below. Also with such a high difference in electronegativity of these two atoms more ionic character will be witnessed.


Molecular Orbitals

Images of the molecular orbitals can be visualised by GaussView. They represent each orbital solution to the Schrödinger equation, in other words the Φs, one for each MO energy level. [1]

  1. ↑ http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year1/10_mos_n2.html


There are over 90 orbitals found , 41 of which are occupied, and each can be described by the interactions of the atomic orbitals. Five have been explored here.


When looking at diatomic molecules the MOs are the simple interaction between the AOs. However when looking at larger molecule you talk about the MO fragments. This is the non-bonding Cl 2 p orbitals. They are too different in energy to interact with the Al orbitals so remain non-bonding. There are 12 with similar energies and shapes that can be attributed to the different orientations and phases of each orbital.


These two are a pair of MOs created by interactions between the same AOs; the s Cl fragmant and the s Al. However one is an in-phase interaction (left) which produces a filled bonding orbital and the other out of phase interaction (right) which produced an anti-bonding orbital which is also filled. Both are occupied so these are not the orbitals responsible for bonding in this molecule.


This is another bonding (left) and non-bonding (right) pair of MOs. These were caused by the interaction of the 3p Cl fragment and the 3p Al. The bonding is filled and the anti-bonding is empty so it is this orbital that is responsible for the bonds in this molecule.

S2

S2

The optimisation file is liked to here

Proof of Structure Convergence


         Item               Value     Threshold  Converged?
 Maximum Force            0.000039     0.000450     YES
 RMS     Force            0.000039     0.000300     YES
 Maximum Displacement     0.000067     0.001800     YES
 RMS     Displacement     0.000095     0.001200     YES
 Predicted change in Energy=-2.624039D-09
 Optimization completed.
    -- Stationary point found.

There is zero net force and displacement so the optimization has successfully converged and is complete.

Summary Information

S2 Optimised Information
S2
Calculation Method RB3LYP
Basis Set 6-31G(d,p)
E(RB3LYP)/ au -796.32599779
RMS gradient / au 0.00002267
Point Group D*H
S-S bond length / A 1.92952
S-S bond angle / degrees N/A

Molecule Vibrations

The 3N-5 rule used for linear molecules gives 3x2-5= 1. This is supported by the frequencies found from computational analysis as seen in the image above. This is due to the simple stretching of the bond.


Charge Distribution

Sulfur has an electronegativity of 2.58. However when both atoms have the same electronegativity the charge is equally distributed across the molecule.


Molecular Orbitals

Images of the molecular orbitals can be visualised by GaussView. They represent each orbital solution to the Schrödinger equation, in other words the Φs, one for each MO energy level. [1]

  1. ↑ http://www.huntresearchgroup.org.uk/teaching/teaching_comp_lab_year1/10_mos_n2.html

There are over 30 orbitals found , 16 of which are occupied, and each can be described by the interactions of the atomic orbitals. Some examples are given below.


3 s orbitals from each Sulfur atom forms a bonding (left), anti-bonding (right) pair of orbitals shown above.


The 3px from each sulfur interact to form a bonding (left) and an anti-bonding (right). However both are filled so no bond is formed from these MOs.

The 3pz from each sulfur interact to form a filled bonding (left) and a unfilled anti-bonding (right). Therefore this results in a sigma bond being formed between the two sulfur atoms.

The 3py from each sulfur interact to form a filled bonding (left) and a unfilled anti-bonding (right). Therefore this results in a pi bond being formed above and below the plane of the two sulfur atoms.

Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=Rep:Mod:HB9151&oldid=816925"