Rep:Mod:FourToDoomsday
Abstract
Hartree-fock and density functional theory calculations have elucidated the transition states, activation barriers and intrinsic reaction coordinates for two well known pericyclic processes. Convergence times of calculations was adequate although affected significantly by guess inputs and in many cases redundant coordinates had to be employed for transition states to be isolated. Rendered MOs correspond agreeably to that expected by qualitative orbital correlation methods. SCF energies confirm expected selectivites of these reactions/'chemical intuition' about their progression.

Sigmatropic Rearrangements
1,5-Hexadiene is both the reactant and product of the [3,3] sigmatropic rearrangement. Because of this the reaction is energetically neutral and we merely need to identify the energy and nature of the transition state to know the kinetic feasibility of it at any temperature. This precise reaction, the Cope rearrangement, has been the subject of some controversy and significant computational investigation to discern how it proceeds[1]; with some computational studies concluding the identity of the TS to be any of:
- A 1,4 diradical cyclohexane ring
- Two allyl radicals
- A singlet state aromatic pericyclic moiety.
Meanwhile, it should also be stated that the nature of substituents, which are not present here, greatly impact the placement of the transition state between these three extremes[2][3] In this work we will discount consideration of the former and assess the relative levels of the latter two in the simplest Cope rearrangement. First we must optimise the free molecule:
Due to its chain structure 1,5-hexadiene can adopt a range of mechanically stable conformations through rotations about carbon carbon bonds, and these can be cataloged most easily by whether the saturated midsection of the molecule is gauche (dihedrally carbons 2 and 5 occupy positions 60° from each other) or anti (180°). Hartree-fock calculations using a 3-21G basis set have identified some examples of both orientations. Somewhat surprisingly, the calculations returned a non-zero dipole for a conformation containing a centre of inversion (shown below), but this was found to be optimised out (so to speak) by B3LYP/6-31G(d) level calculations (the input coordinates were also symmetrised very tight to Ci beforehand). The same calculation also returned an energy that was quite drastically different (~50kcalmol-1 less negative, although of course they cannot be compared). This higher optimised structure will be useful in assessing the feasibility of transition state calculations later on.
Anti Conformations
|
| ||||||||||||||||||||||||||
|
|
The predicted IR spectrum of this conformation would be expected to be not drastically dissimilar to the literature, as it is the lowest energy anti conformation, and so a large population should adopt it at standard conditions. B3LYP/6-31G(d) frequency predictions are reasonably consistent with the known[4] spectrum, with deviations for the terminal CH2 and CH wagging modes of 28.4 and 39.4 wavenumbers. Low frequencies returned by the calculation are within adequate bounds.
Supplementary information
Sum of electronic and zero-point Energies= -234.469212 Sum of electronic and thermal Energies= -234.461856 Sum of electronic and thermal Enthalpies= -234.460912 Sum of electronic and thermal Free Energies= -234.500821
Low frequencies --- -18.6296 -11.7148 0.0003 0.0007 0.0009 1.8362 Low frequencies --- 72.7321 80.1450 120.0238
Gauche conformations
There are a larger number of possible gauche conformations, and several of them can also reasonably be described as chiral. This was initially thought useful for investigation however upon inspection the energies for the reported conformation 6 and it's enantiomer are identical to 5 decimal places (6.275*10-4kcalmol-1 error), and so this course of investigation was ceased.
|
|
Transition States
General comments
One can apply an approximation of conformational analysis to preemptively determine what is likely to be the lowest energy transition state of a reaction under consideration, lowering computation time. Since we are dealing with a circular arrangement of six carbon atoms here the conformations of cyclohexane are of importance. Hence further discussion will be split into the chair and boat form of the Cope rearrangement transition state.
Unless otherwise stated, calculations were done to the HF/3-21G level, and symmetrised (tight criteria) to the expected point group of their respective transition states. Opt=noeigen was specified and force constants were calculated once for all TS identification calculations and always for all IRC calculations.
Chair Transition State
Since the frequencies of a moiety as calculated by Gaussian are proportional to the second derivative of the energy, a negative value present in the output implies a maximum in potential, which is useful in determining the existence of a transition state. Standard optimisation (berny) algorithms have been found to converge on the chair-like TS easily, using two allyl fragments spaced 2.2Å apart as input. These were previously optimised to the HF/3-21G level. The frequency of the oscillation about the TS was returned as -817.79cm-1.
|
|
Further to this, a regular optimisation of the transition state at the same level, specifying frozen coordinates for the forming/broken bonds, was done to try and identify any minima in relation to the position of C2 and C5. This returned identical nuclear coordinates so it was concluded that this had already been achieved (The results table is identical to that shown above so is not deemed useful to reproduce it).
Further QST2 HF/3-21G calculations were conducted using the previously reported anti configuration as both reactant and product (atomic numbering had to be reordered to allow for the differing connectivity due to the rearrangement). Unfortunately this was acting under the assumption that dihedral rotation to the syn chair like atomic configuration would be identified by the optimisation. In fact the reactant and product moieties were too dissimilar to the transition state and this was found to not converge; The optimisation algorithm merely translated the two allyl fragments relative to each other (figure 2). As we will see later, an identical calculation with syn input coordinates (a very unstable conformation mechanically) was the first which identified a boat TS and this converged much easier.
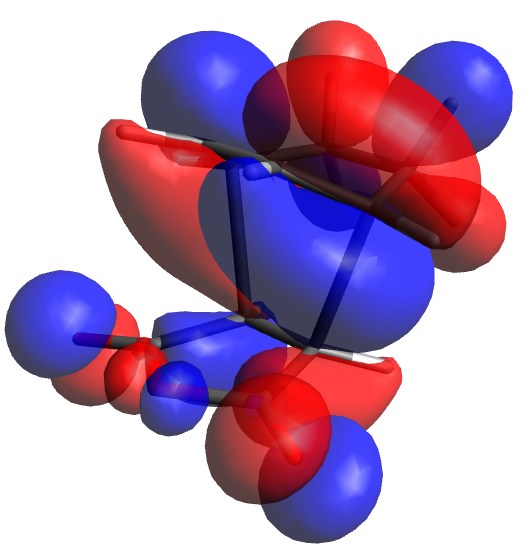
Returning to the previously successfully identified chair TS, redundant coordinates were altered to derivative (ie numerical hessian matrices were used) and a third optimisation (Berny) was done to the B3LYP/6-31G(d) level. As can be seen from the JMol pop-up this shortened the allyl-allyl distances as well as removed the dipole returned by the previous calculation.
| Result | Value |
|---|---|
| Calculation Type | FTS |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -234.55698303 |
| RMS Gradient Norm | 0.00001186 |
| Imaginary Freq | |
| Dipole Moment | 0.0000 |
| Point Group | C1 |
| Logfile | File:TS CHAIR BERNY 631.LOG |
| 3D View |
|
Having concluded that this TS had been successfully identified, an IRC was conducted with N=50 points in both directions[5]. As expected, the IRC path was entirely symmetrical. At the edges, it can be seen that the molecule begins rotating about the bonds immediately adjacent the newly formed one, appearing to move towards a C2 symmetric gauche conformation. Interestingly, calculations to the B3LYP/6-31G(d) level[6] produced a much less smooth IRC curve, with the most maximum point much higher than expected, seemingly due to C-H bond lengths spontaneously decreasing as one tracks over the transition state. Interestingly it is not confined to this IRC, with similar behavior identified during the Boat calculations. The only explanation that can be offered regarding its origins is that it is an effect of using d polarisation without concurrent p polarisation on H. As such, all discussion from now on will relate to the Hartree Fock optimised TS.
 |
 |
Boat Transition State
The boat transition state was identified using broadly the same methods as the chair ie. initially by placing two allyl fragments 2.2Å apart. The negative/complex frequency was in this case -839.95cm-1, and the energy is significantly higher than the chair optimised to the same theory level (10.37kcalmol-1). As mentioned earlier a QST2 calculation using syn-1,5-hexadiene was also done and as can be seen differs from these results only in the last decimal places i.e. gives essentially the same result. Upon inspection of the atomic displacements it was noticed that the oscillation associated with the transition state involves a quite substantial movement of the centre of mass of the system, () perhaps implying the larger energetic requirement (or rather, activation energy) is a manifestation of this. However upon inspection of the displacements returned in the log file this was found not to be true as the boat actually involves a smaller oscillation of these two carbons (0.12 vs 0.13Å). Hence we should conclude that the high energy of the boat transition state is a result of steric/pauli repulsions associated with that configuration, not of the coordinates immediately around it.
|
|
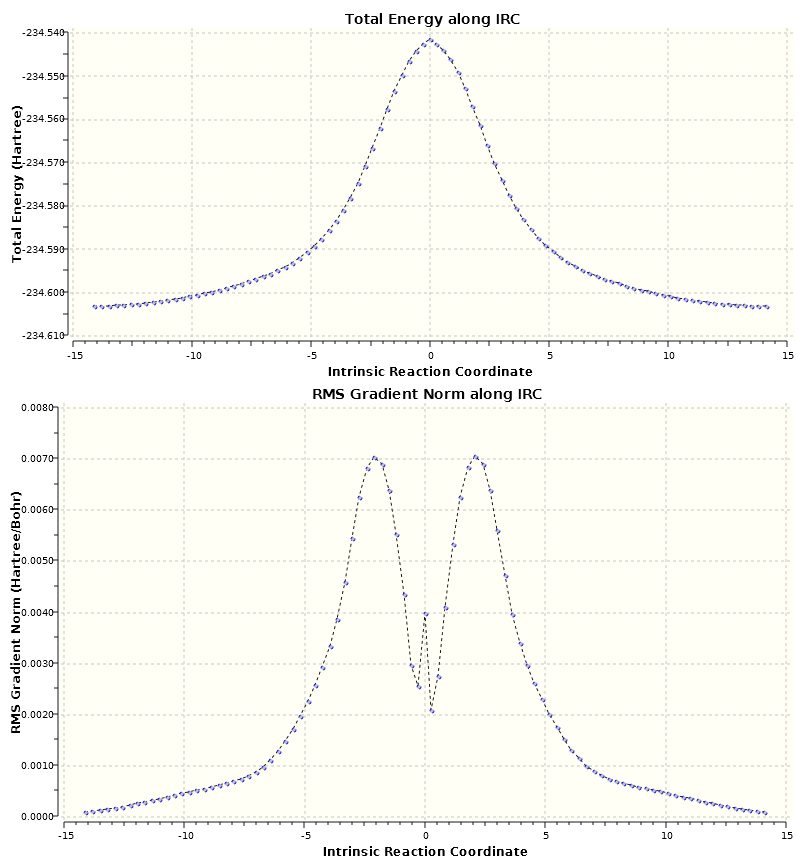
IRC calculations[7] using a 6-31G(d) optimised structure were non ideal (N=100, both directions), with the C-H bonds mysteriously shortening at precisely the transition state. It was discovered that this was the result of the input coordinates, as the calculation took precisely the bond lengths found at the apex rather than the geometries immediately surrounding it, implying the transition state was not being optimised. In an attempt to rectify this, bond lengths were manually altered to those found in the two adjacent IRC points. This somewhat alleviated the problem but once again it was not as smooth as the Chair IRC
 |
 |
|
Supplementary Information
Frequencies -- -839.9479
Red. masses -- 8.4533
Frc consts -- 3.5138
IR Inten -- 1.6218
Raman Activ -- 26.9998
Depolar (P) -- 0.7500
Depolar (U) -- 0.8571
Atom AN X Y Z
1 6 0.40 -0.06 0.03
2 1 0.02 0.01 0.03
3 1 -0.27 -0.06 0.03
4 6 0.00 0.12 0.00
5 1 0.00 0.05 0.00
6 6 -0.40 -0.06 -0.03
7 1 0.27 -0.06 -0.03
8 1 -0.02 0.01 -0.03
9 6 -0.40 -0.06 0.03
10 1 -0.02 0.01 0.03
11 1 0.27 -0.06 0.03
12 6 0.00 0.12 0.00
13 1 0.00 0.05 0.00
14 6 0.40 -0.06 -0.03
15 1 -0.27 -0.06 -0.03
16 1 0.02 0.01 -0.03
Discussion
The activation energies (relative to the lowest energy anti conformation) for the two TS geometries are 34.34kcalmol-1 and 43.05kcalmol-1, affording them relative errors of 2.2 and 3.7% from the provided values. This affords us certainty in one conclusion: Even assuming both of these reaction pathways are accessible, the rate of reaction via the chair TS at r.t. will be a factor of faster than that via the boat, confirming the 'conformational' treatment that the chair is the known geometry.
The dichotomy mentioned in the introduction between describing the TS as a diradical or a fully aromatic system cannot be resolved in favour of the former merely because the returned transition states are singlet; homolytic cleavage of the C3-C4 bond will not change the spin state of the overall system. However in light of the short bond lengths it is unlikely electrons are localised on the allyl fragments. Additionally, using the Aufbau principle we can say that the most likely biradical system is one in which the HOMO/LUMO are energetically degenerate, however at this theory level this is strictly not the case (0.44Ha gap for the boat, 0.14 for chair).
References
- ↑ R.V. Williams, Chem. Rev., 2001, 101, 1185
- ↑ J.J. Gajewski, Acc. Chem. Res., 1980, 13, 142
- ↑ J.J. Gajewski, N.D. Conrad, J. Emrani and K.E. Gilbert, ARKIVOC, 2002, 4, 19
- ↑ K.O. Patten, A. Lester, J. Am. Chem. Soc., 1985, 107(20), 5594
- ↑ S. Ingram, 2014 DOI:10042/28125
- ↑ S. Ingram, 2014 DOI:10042/28126
- ↑ S. Ingram, 2014 DOI:10042/28127
Diels Alder Reactions
Ethene + Butadiene
Reactant Studies
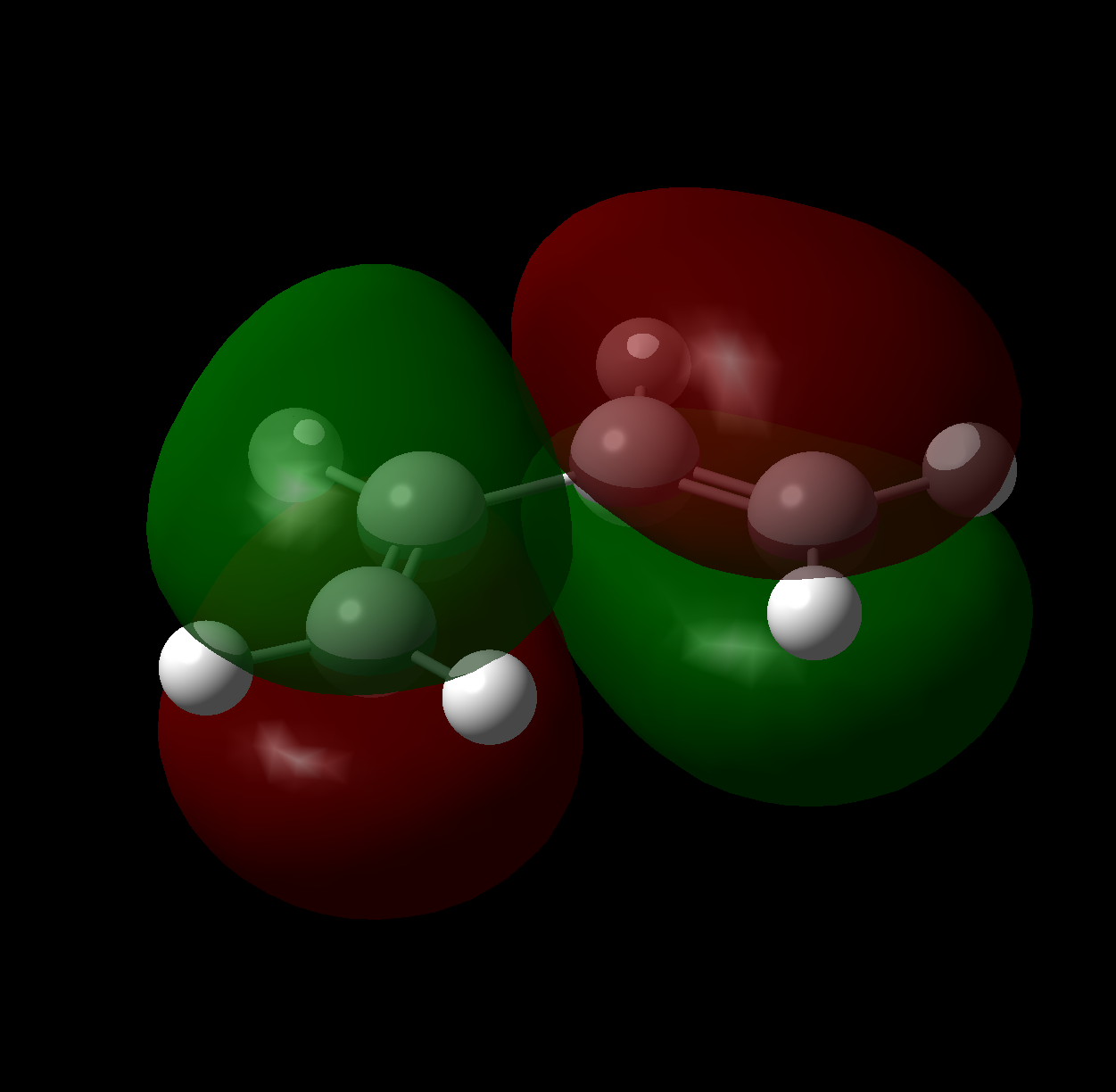
It is well known that the movement of electrons during pericyclic reactions can be described by the Woodward-Hoffman selection rules and through orbital correlation. The thermal 4+2 cycloaddition of ethene and cis-butadiene offers a computationally non-intensive method to study this. To begin with the molecular orbitals of cis-butadiene were calculated to the AM1 level, as shown in the figures below.
|
 |
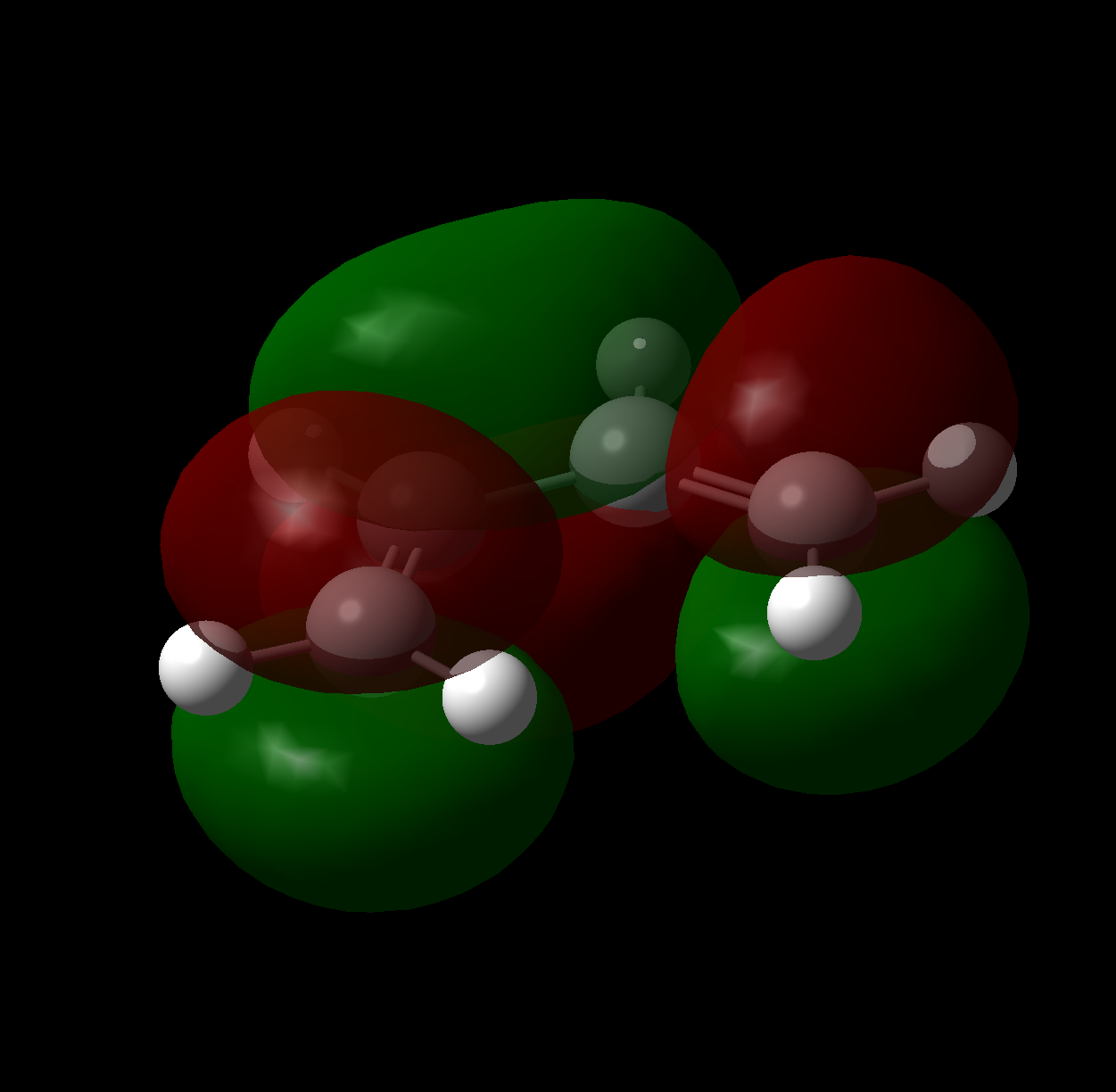 |
Due to the Hückel topology of the transition state it is useful to define the behavior of orbitals relative to a plane of symmetry intersecting the second and third carbons. Under this treatment the HOMO is antisymmetric with respect to reflection and the LUMO is symmetric. Of course this is a rather basic model of the conformational structure of butadiene in solution, and is in fact a maximum in energy (negative frequencies present in subsequent Opt+Freq calculation File:CIS BUTADIENE MOS 631.LOG confirm this), but nicely illustrates the orbital symmetry for comparison later.
Transition State
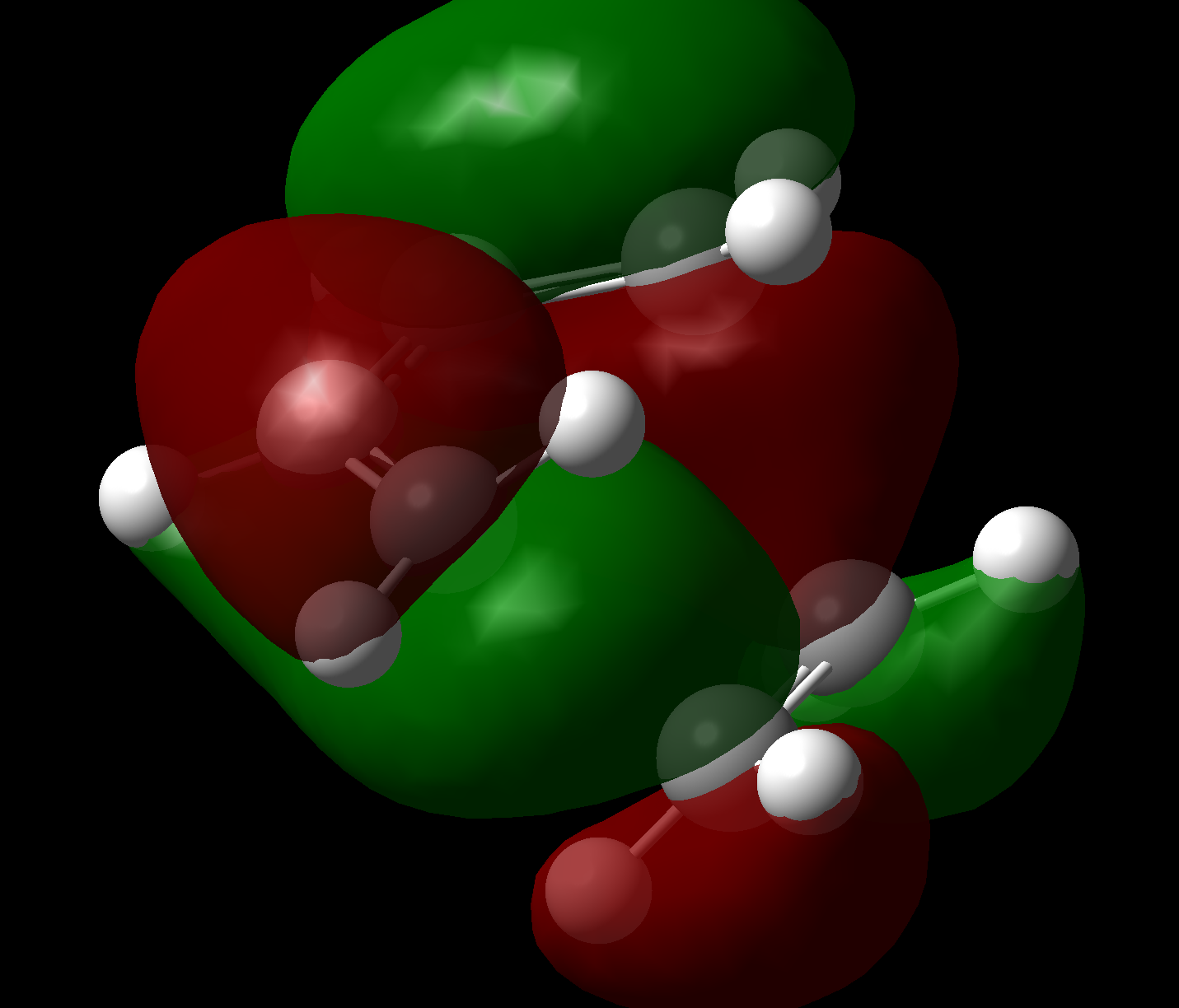
Transition states in which ethene approaches from the top or bottom face are identical for this reaction due to the lack of stereo/regiochemistry in the reactants. QST2 isolation of the maximum was done from the product backwards (so to speak), by taking the coordinates of a molecular mechanics (MMFF94s) optimised [2,2,2] bicyclic system (with one bridge containing an olefin), replacing one of the C2H4 bridges with two hydrogens, and setting the remaining C-CH2 bond lengths to 1.8Å. Once again, opt=noeigen was specified although in this case geom=connectivity was also found to be required.
 |
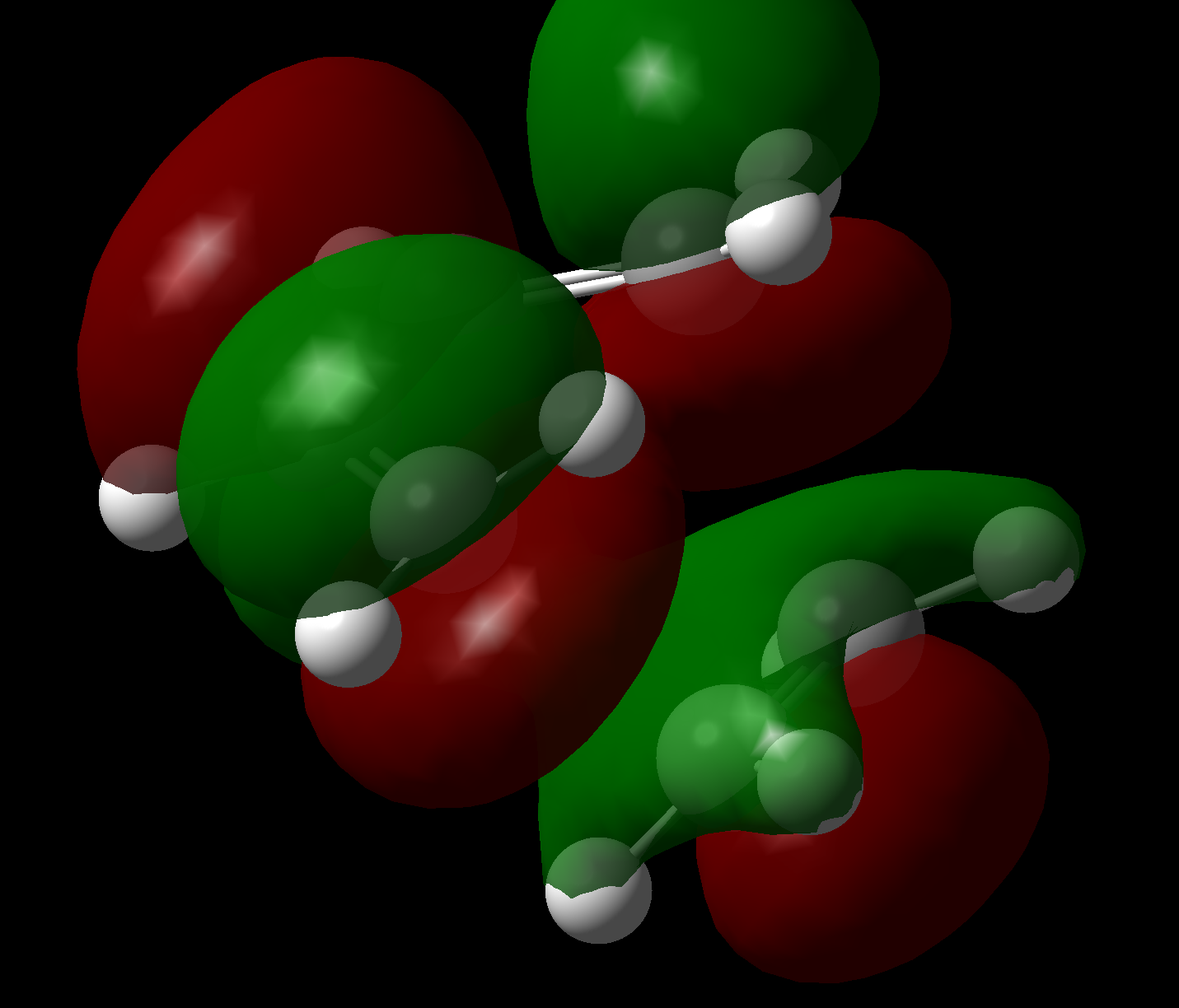 |
It becomes immediately obvious that the cis-butadiene MOs are the overriding factor in the ordering of the transition state orbitals, in that the HOMO remains antisymmetric and the LUMO remains symmetric. This is not thought to be controversial given that:
- simple Hückel theory tells us that butadiene's HOMO and LUMO will be energetically between those of ethene's (due to them arising from combinations of two ethene-like fragments);
- for both molecules there is no difference in orbital coefficient magnitude on any carbon between the HOMO and LUMO - merely the signs of the atomic orbitals comprising them are inverted
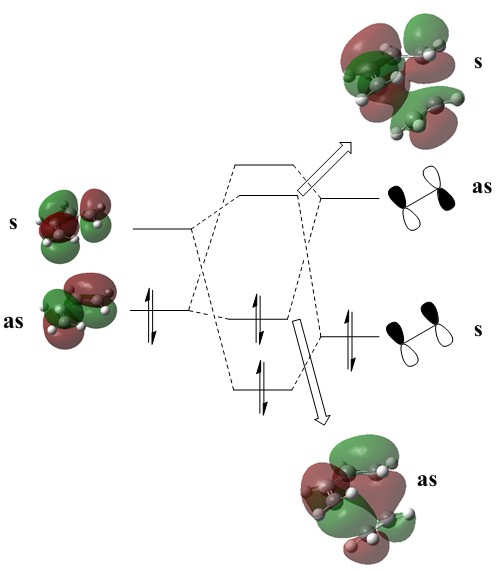
Hence, combining these two factors, the electronic stabilisation relative to the butadiene MOs will be approximately minimal in the case of the HOMO and maximal in the case of the LUMO, and the energy gap between the two should increase slightly (figure 9). This was adequately found to be the case at the B3LYP/6-31G(d,p) theory level (a new MO set was generated for butadiene), where HOMO-LUMO gaps were found to be 0.147 and 0.159Ha respectively.
The internuclear distances for the forming bonds are 2.271 and 2.273Å, implying some small degree of asymmetry in the reaction as it proceeds. However, given that both the TS as calculated is within the 'Loose' tolerance for the Cs point group and that the animation of the complex frequency (which occurs at -525.18cm-1) is highly plane symmetric (ie the bonds form synchronously), we may assume this to be an instance of accrued errors in the calculation rather than a physically meaningful conclusion.
| Result | Value |
|---|---|
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -234.54389635 |
| RMS Gradient Norm | 0.00003917 |
| Imaginary Freq | 1 |
| Dipole Moment | 0.3940 |
| Point Group | C1 |
| Logfile | File:DIELS ALDER TS 3RD.LOG |
| 3D View |

To determine the extent of bonding in the transition state a search for the cyclohexene motif was conducted on the Cambridge Crystal Structure Database, specifying bond distances for the C-C bonds on the appropriate ring positions. The results show the majority occur between 1.52 and 1.54Å and the largest is 1.78Å (peaks at longer distances are for fused ring systems and have been discounted). Hence the bonds present in the product are not explicitly formed at this stage, although it should be noted that the distance is below twice the carbon VdW radius (1.70Å[1]), and so there is certainly an attraction present. This is corroborated by the lowest real frequency predicted during the calculation (fig. 12), which can be described as a bending oscillation about the forming C-C bonds. This implies that the calculation is treating them as real bonding interactions with associated force constants.
 |
 |
The simplistic nature of conducting calculations on just transition states results in the means of activation not being considered quantum mechanically. Due to this it was feared that isolation of a (photochemically induced) Möbius transition state was possible in this case, however given the relative ease of isolation of the Hückel TS it became clear this would likely require meticulous computations using more exotic theories. Another interpretation of the identity of the transition state found herein is the notion that Möbius topology pericyclic reactions are more complex than reactant > transition state > product and involve radical processes. In either case, no further investigation was conducted on this.
1,3-Hexadiene + Maleic Anhydride
The reactants studied presently have a larger extent of planar delocalisation in their ground states than those modelled in the previous section. This introduces the possibility of more complex electronic effects on the stereochemistry of the product, of which the the endo- and exo-adducts may be identified. The conventional explanation for the selective formation of the endo product in most cases of 4+2 cycloadditions is secondary orbital overlap[2] of the p functions localised on carbons that are not immediately taking part in the reactions, but which nevertheless occur during the frontier orbital encounter which drives the reaction; specifically that identified in the previous section as the diene HOMO and dienophile LUMO.
However it has been proposed since 1987[3] that sterics are as important a factor in favouring the endo form in reactions in which maleic anhydride (hereinafter MA) is the diene. The qualitative justification is that two saturated rings stacked parallel engender a less bad steric clash than a ring and an aliphatic bridge (although this is only relevant when the product is a bicyclic molecule). This was recently verified in the case of reaction of Cyclopentadiene with MA[4] using very high level calculations.
Herein we wish to; first, replicate the observed selectivity of the reaction using DFT calculations; and second, probe the feasibility of these two explanations.
Exo Transition State
This transition state was found to be much easier to identify than the corresponding endo. The product input geometry was first optimised to the AM1 level (not symmetrised), and the 'reactant' guess taken by adjusting bond orders appropriately (as geom=connectivity was specified) and forcing planarity about all sp2 carbons. The forming C-C bond was set to to 2.0Å. A QST2 calculation was done with these inputs and isolated the transition state in 39 steps. Force constants were calculated once.
| Result | Value |
|---|---|
| Calculation Type | FREQ |
| Calculation Method | RB3LYP |
| Basis Set | 6-31G(d) |
| Charge | 0 |
| Spin | Singlet |
| E(RB3LYP) | -612.67931092 |
| RMS Gradient Norm | 0.00000992 |
| Imaginary Freq | 1 |
| Dipole Moment | 5.5499 |
| Point Group | C1 |
| Logfile | File:SI Exo QST2.log |
| 3D View |
Inspection of the computed MOs showed them to be not unlike those of the prototypical Diels Alder reaction studied earlier, with the HOMO being antisymmetric with respect to plane reflection. Interestingly, there is little to no electron density on the carbons α to where the new bonds are forming, and where the strongest overlap expected in the endo form would occur (we will return to this later). There is, however, an in phase interaction between the oxygen p orbitals and the C-H σ bonds directly above them, which can be more easily demonstrated by reducing the isosurface value to 0.1. Although it is not a п-п interaction it is still believed to be correct to refer to this feature as 'secondary orbital overlap'. Nonetheless it is an unexpected result given the importance attached to orbital effects when explaining the relative instability of this transition state.
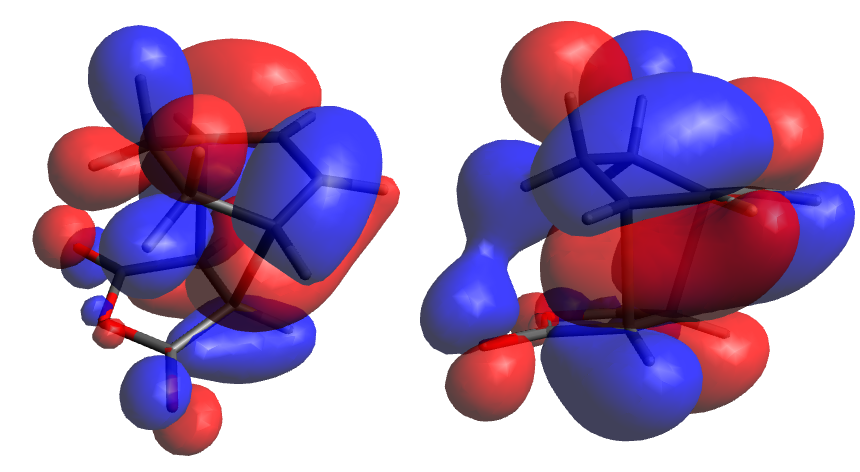
Oddly, electron density present on the central oxygen fragment appears to be inhabiting a p orbital perpendicular to those on the carbonyls. While this is consistent with the plane asymmetry of the MO, it is a strange occurence as it cannot interact either constructively or destructively with the frontier orbitals it is immediately directed towards.
Supplementary Information
Item Value Threshold Converged? Maximum Force 0.000031 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000980 0.001800 YES RMS Displacement 0.000256 0.001200 YES Predicted change in Energy=-1.225920D-08 Optimization completed.
Sum of electronic and zero-point Energies= -612.498013 Sum of electronic and thermal Energies= -612.487662 Sum of electronic and thermal Enthalpies= -612.486718 Sum of electronic and thermal Free Energies= -612.534264
Endo Transition State
As eluded to earlier, this proved considerably more problematic to isolate. A brief overview of the methods attempted is reported below:
- Initial calculation using precisely the same method as the Exo (AM1 optimised product guess, 2.0Å C-C bond length reactant guess):
# opt=(calcfc,qst2) freq b3lyp/6-31g(d) geom=connectivity
did not converge on the TS after 138 steps[5]. - Of the intermediate steps, the one closest to the expected geometry was symmetrised to the highest available point group (Cs in this case) and a berny optimisation was attempted. No geom keyword was specified. The calculation output returned that virtual bonds had to be added between seemingly inconsequential atoms (ie two hydrogens that had a somewhat close approach) before stopping. Redundant coordinates were appended such that the forming bonds were specified as such and the suggested non physical bonds were removed. After this returned the same error it became clear that geom=connectivity would have had to be specified for this precise calculation to be continued. However this was non ideal, as the bond orders could not be assumed to be the same as the exo TS and would likely lead to a prohibitive number of optimisation steps.
- To attempt to isolate the TS at a lower level, the d polarisation was removed from the basis set, as was the frequency calculation. Force constants were changed to be calculated always.
- This succeeded in finding the TS[6] and so a regular optimisation was conducted by freezing the C-C bonds under modredundant (with d polarisation added). All discussion hereinafter will be with reference to the output of this[7] calculation.
As expected, the HOMO of the system arises from combinations of the same MA and 1,3-cyclohexadiene frontier orbitals as the other transition state, and hence contains little in the way of secondary orbital interactions; indeed, the carbonyl oxygen orbitals are exactly out of phase with respect to the diene fragment, and the only section of the dieneophile that can share electrons in the HOMO (the central oxygen p orbital) does not encounter the π system above isosurface values of 0.07, implying not much electron density is exchanged and there is a quite weak energetic benefit from it.
Nonetheless this transition state is, as expected, more negative in energy and so the experimental result has been replicated. The implication is that the sterics of the approach of MA with a saturated bridge strain the system less.
Supplementary Information
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000004 0.001800 YES RMS Displacement 0.000001 0.001200 YES Predicted change in Energy=-1.497927D-11 Optimization completed.
Sum of electronic and zero-point Energies= -612.502143 Sum of electronic and thermal Energies= -612.491790 Sum of electronic and thermal Enthalpies= -612.490846 Sum of electronic and thermal Free Energies= -612.538330
Discussion
The energy difference between the two isolated transition states is 10.73kJmol-1. No studies containing the relative energy difference computed to this theory level were found (B3LYP/6-31G(d,p) is more often employed). Using this and the Arrhenius/Boltzmann equation a theoretical selectivity at standard conditions may be deduced (assuming the reaction has gone to completion the relative rates will correlate precisely with the concentrations):
Activation energies may be easily calculated from computational outputs of the reactants but are not needed in this case. Nevertheless this implies 98.7% endo, actually less than that usually found experimentally, which is in excess of 99%. Although the error relative to the observed is small, larger energy differences will not drastically increase the predicted selectivity as the relationship is one over the exponent. Under this treatment the 'final' 0.3% would correspond to an extra 2.7kcalmol-1 energy difference between the two transition states. It is concluded that this is a sufficiently small deviation to still draw conclusions from these calculations.

Due to the complications experienced in isolating the endo transition state, some skepticism was extended over the validity of the geometry provided, especially considering it lies on the most useful reaction profile of the two. An IRC[8] was concluded the best method to confirm this. As shown in fig. 15, the local reaction coordinates about the peak (only one direction was computed) are extremely smooth, confirming a successful optimisation has been done. Interestingly, the peak of the RMS gradient occurs past half way through the reaction progression, and the steepness increases thereafter. This feature cannot be ascribed to insufficient points being calculated , and hence the horizontal axis not extending far enough, since it only ran to 18 of the specified 50. Appending irc=tight and int=ultrafine (as suggested by the Gaussian manual) actually returned fewer points[9] (only 17) so the calculation must be assumed to be complete.
More qualitatively, we may compare the bond lengths to those computed in the literature to check the efficacy of the calculated geometries. A meta study[10] of retro Diels Alder transition states (which will, in theory, be identical to those for the forward reaction) has been found, mostly computed to the B3LYP/6-31G(d,p) level. The addition/removal of p polarisation is unlikely to affect the simulation of Carbon-Carbon bonds with this theory and so a comparison of bond lengths/mechanical properties is not inappropriate here. The 'separation' at the forming bonds have relative errors of 0.04% and 0.09%, and the energy difference between TS and product (or activation energy in this case as the referenced work relates to retro Diels Alder reactions) deviates by 5.06% (45.8 vs 43.6kcalmol-1). Interestingly (but perhaps coincidentally), this is very similar in magnitude to the energy difference mentioned earlier that was required to replicate the observed endo:exo selectivity. It would, however, be presumptuous to assign this over prediction as the origin of that error.
In light of both the further calculations (IRC) and ostensible agreement with reported literature (selectivity and activation barriers), the relative SCF energies arrived at presently can be described as credible, and hence any intuitive conclusions reached regarding the electronics of these reactions (from MO geometry etc.) are justified.
Returning to which, the indication that there is a comparable favourable overlap in both transition state geometries can be more rigorously defined; Non Covalent Interaction surfaces have been produced (using the method provided here) from the formatted checkpoint files of both transition states, and neatly confirm this prediction. As can be seen in the figures, attractive (green) forces stabilise the anhydride moiety which arise from both the saturated and unsaturated bridges. Indeed, the stabilisation appears larger in the case of the exo (the multicoloured surfaces about the forming bonds are a characteristic of the calculation and may be ignored).
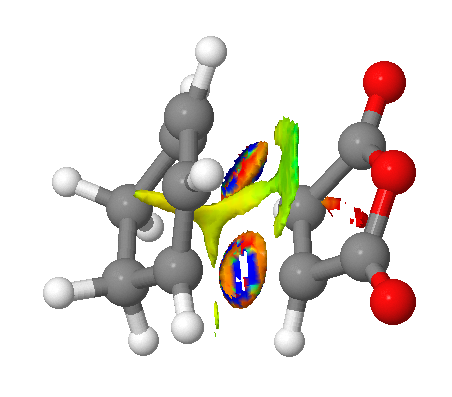 |
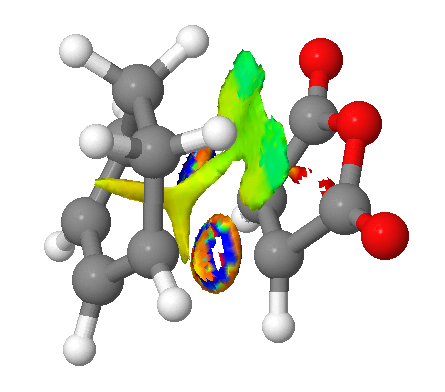 |
This is entirely consistent with that found in reference 4 ie. that the orbital contribution to the endo selection rule is minimal in comparison to steric effects, and is not a trivial conclusion given the differing nature of the dienes (cyclopentadiene vs 1,3-cyclohexadiene) in these two works.
- ↑ A. Bondi, J. Phys. Chem., 1964, 68(3), 441
- ↑ R. Hoffmann, R.B. Woodward, J. Am. Chem. Soc., 1965, 87, 4388
- ↑ M.A. Fox, R. Cardona and N.J. Kiwiet, J. Org. Chem., 1987, 52, 1469
- ↑ I. Fernández, F.M. Bickelhaupt, J. Comp. Chem., 2014. 35(5), 371
- ↑ S. Ingram, 2014, DOI:10042/28187
- ↑ S. Ingram, 2014, DOI:10042/28188
- ↑ S. Ingram, 2014, DOI:10042/28190
- ↑ S. Ingram, 2014, DOI:10042/28202
- ↑ S. Ingram, 2014, DOI:10042/28205
- ↑ D. Birny, D. K. Lim, J.H.P. Koh, B.R. Pool and J.M. White, J. Am. Chem. Soc, 2002, 124, 5091
Conclusions/Outlook
Pericyclic transition states have been located for three six electron processes. The Cope rearrangement may proceed through one of two transition states that adhere to the relative energies predicted by the cyclohexane conformations, although their geometry procludes description as a diradical. Orbital distributions in the Diels Alder reaction of butadiene with ethylene have been found to exhibit non contraversial arrangements. This is in contrast with that of Maleic Anhydride and Cyclohexadiene in this work, which suggests orbital overlap/electronic interactions in general do not factor as much in the stability of the transition states (or factor with similar magnitudes) as sterics.
Beyond these conclusions further calculations would be beneficial to understanding these reactions: solvent effects (or at least their simulation with reasonably non intensive Density Functional Theory) on the transition states can be analysed; NMR prediction of a ghost atom placed in the centre of the [3,3] sigmatropic rearrangement transition state could settle the extent of aromaticity present; and asymmetry can be introduced into the systems (via isotopic labelling, or merely substitution of functionality) would allow us to check the stereochemical outcome is in alignment with that predicted by the dis-rotatory nature of the Diels-Alder transition state.