Rep:Mod:FolarinModule3

Characterisation of transition structures on potential energy surfaces for the Cope Rearrangement and Diels Alder cycloaddition reactions

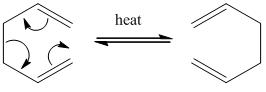
According to the reference, the Cope rearrangement is a [3,3]-sigmatropic rearrangement, with only carbon atoms in the ring. The main theme of this tutorial is to observe the boat and chair transition states of a Cope rearrangemenet, and observe whether the reaction occurs in a concerted fashion. 'This reaction involves two non-conjugated pi bonds that have to overlap across space and a sigma bond in the chain joining the two pi bonds'. As this is a pericyclic reaction, there are no intermediates involved, only a transition state, whose energy determines the overall rate of the reaction.

The Cope Rearrangement Tutorial

Optimizing the Reactants and Products :

The computational methods involved in this exercise are based on the Hartree Fock approach as well as Density Functional Theory. Essentially, density functional theory is one in which ground state molecular properties are calculated based on electron density, which can be measured experimentally by X-ray diffraction or electron diffraction techniques. The Hartree Fock approach is essentially quite different from the density functional approach as it relies on wavefunctions. The trial functions used in the Hartree Fock approach are essentially products of one electron wave functions. The best energy that can be obtained using this technique is called the Hartree Fock limit.

Exploring Conformations of 1,5 Hexadiene.

General Procedure: At the HF/3-21G level of theory, a variety of conformations of 1,5 Hexadiene were successfully optimised. These models were built by generating chemdraw models, which were then visualised in three dimensions using ChemBio3d Ultra 12.0, after which a quick MM2 force field minimisation calculation was run. Any models containing atoms which were improperly located could be fixed with the 'move objects' icon, and then another MM2 calculation carried out. The MM2 minimised models were then saved as Gaussian input files, to be re-opened for HF/3-21G optimisation in Gaussview 3.09. Good use was made of the appendix(lab manual) in generating starting geometries to be fed into in ChemBio3D Ultra 12.0, before optimisation in Gaussian, via Gaussview 3.0.9.

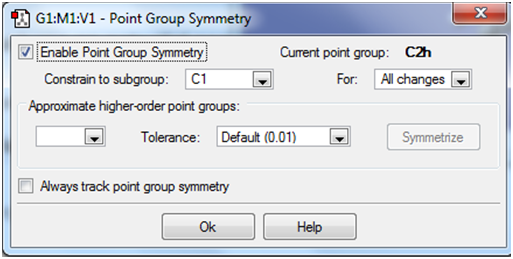
Optimising 'anti' conformations The first conformation to be optimised was one in which the central four carbon atoms had an approximately 'anti' linkage. Four such conformers were generated in total, with their Energies in Hartrees noted, along with their point group symmetry. Total energies were noted from the 'Results' section in the main Gaussview toolbar under 'Summary'. Point group symmetries assigned, were they are not given as C₁ are in fact approximate higher order point groups. This was determined by selecting the 'Point Group' option under the 'Edit' option within the main toolbar. Enabling point group symmetry and clicking 'Symmetrize' enables the higher order point group to be read off as shown below:

JMOL links have been included below:

anti 1:

anti 2:

anti 3:

anti 4:

LOG file links have also been included below:

anti 1:OPTIMISATIONLOGFILE

anti 2:OPTIMISATIONLOGFILE

anti 3:OPTIMISATIONLOGFILE

anti 4:OPTIMISATIONLOGFILE

A table of key results is shown below.

Conformer	Point Group	Energy/Hartrees	Relative Energy/kcal/mol
anti 1	C2	-231.69260	0.04
anti 2	Ci	-231.69254	0.08
anti 3	C2h	-231.68907	2.25
anti 4	C1	-231.69097	1.06

Optimising 'gauche' conformations: Using the same procedure as described above, models with gauche linkages for the central four carbon atoms were successfully optimised.

JMOL links have been included below:

gauche 1:

gauche 2:

gauche 3:

gauche 4:

gauche 5:

gauche 6:

LOG file links have also been included below:

gauche 1:OPTIMISATIONLOGFILE

gauche 2:OPTIMISATIONLOGFILE

gauche 3:OPTIMISATIONLOGFILE

gauche 4:OPTIMISATIONLOGFILE

gauche 5:OPTIMISATIONLOGFILE

gauche 6:OPTIMISATIONLOGFILE

A table of results is shown below

Conformer	Point Group	Energy/Hartrees	Relative Energy/kcal/mol
gauche 1	C2	-231.68772	3.10
gauche 2	C2	-231.69167	0.62
gauche 3	C1	-231.69266	0.00
gauche 4	C2	-231.69153	0.71
gauche 5	C1	-231.68962	1.91
gauche 6	C1	-231.68916	2.20

A brief note on the relative energies of the conformers: Comparing the energies of 'Gauche 2' and 'Anti 2' for instance, it seems intuitively reasonable that the anti 2 model should be of lower energy than the gauche model given the greater distance between the double bonds within the anti model. It is appreciated however, that this is a very approximate method of determining relative stability and that Hartree Fock calculations are much more detailed. It was predicted that the lowest energy conformer would in fact be this 'anti 2' conformer largely based on the relatively large distance between the double bonds and the anti-periplanar relationship between the central four carbon atoms. A notable weakness of this approach is the lack of orbital overlap considerations. The lowest conformer found was in fact the gauche 2 conformer. Note: Relative energy values have been taken from the appendix in the lab manual.

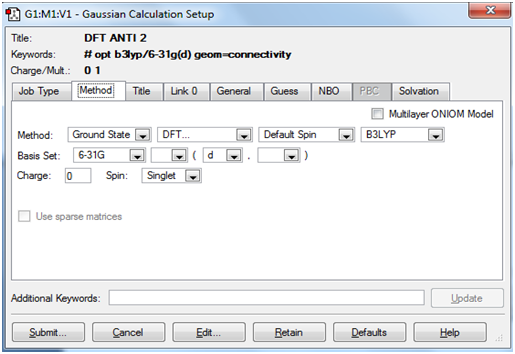
Introducing a higher level of theory for minimisations: The HF/3-21G optimised 'anti 2' conformer was selected to B3LYP/6-31G(d) minimisation

Below is a screenshot of the 'Method tab' within Gaussview showing how the calculation was set up.

A JMOL of the B3LYP/6-31G(d) minimised can be found below:

A LOG file link for the DFT mimimised structure is indicated below:

OPTIMISATIONLOGFILE

It was noted that there was no significant change in the overall geometry,as can be seen from the JMOL model.

A frequency calculation was also carried out on the B3LYP minimised 'anti 2' model. A frequency calculation essentially finds the second derivative of the potential energy surface, and since all of the frequencies located were real and positive, it was confirmed that the B3LYP minimised model was indeed at a mimimum on the potential energy surface.

The screenshot below shows the job and method tabs for the frequency calculation.

Job Tab:

Method Tab:

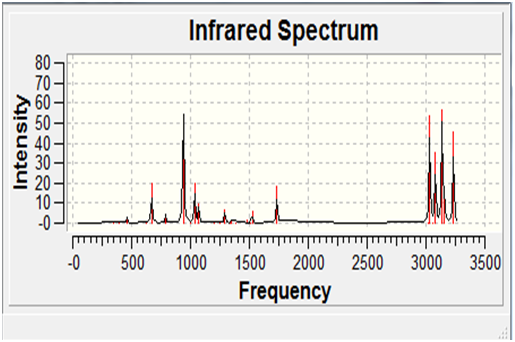
The result of the simulation of the infra-red spectrum is given below:

The LOG file link for the frequency calculation has been indicated:

FREQUENCYLOGFILE

The LOG file link for the HF/B3LYP method frequency calculation output has also been indicated:

FREQUENCYLOGFILE

A summary of the relevant information is given below

Hartree Fock Calculation

Electronic Energy/Hartrees	Sum of electronic and zero point energies/Hartrees at 0K	Sum of electronic and thermal energies/Hartrees at 298.15K
-231.692535	-231.539542	-231.532571

Density Functional Theory Calculation

Electronic Energy/Hartrees	Sum of electronic and zero point energies/Hartrees at 0K	Sum of electronic and thermal energies/Hartrees at 298.15K
-234.611721	-234.469187	-234.461837

Optimising the 'Chair' and 'Boat' Transition Structures

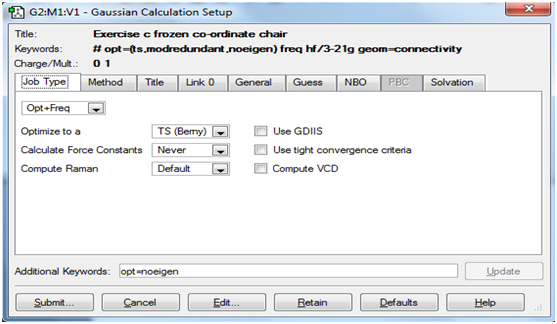
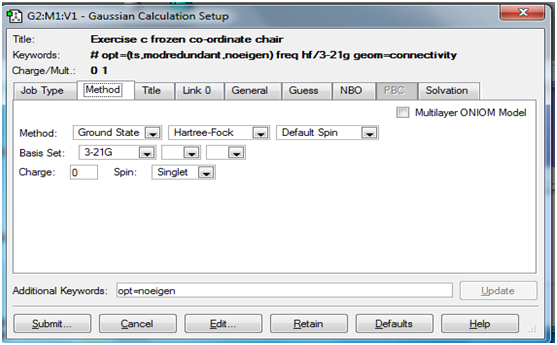
First, optimisation of the chair transition state by computing the force constants at the beginning of the calculation was carried out. Theory(lab manual): A transition state is a maximum on the potential energy surface of the reaction. The procedure in use involves the calculation of a force constant matrix or Hessian in the first step of the optimisation, which is then updated as the reaction proceeds from a reasonable guess of the transition state structure. It is very important to note that the fact that a single imaginary frequency is generated does not mean that we have obtained the correct transition state. The imaginary frequency must be visualised and evaluated as to whether it corresponds to the reaction taking place. As stated in the lab manual, if the guess structure for the transition state is far from the exact structure, then this approach may fail as the curvature of the surface may be significantly different at points far away from the transition structure. A general disadvantage of this approach is the fact that force constant calculation may be an expensive process in terms of computational power.

Method: The allyl(C₃H₅) fragnments required for use in this exercise started off as chemdraw ketches which were then pasted in ChemBio3D Ultra 12.0 and minimised using an MM2 force field calculation. A gaussian input file was saved, and then re-opened in Gaussview 3.09. The allyl fragment was then subjected to HF/3-21G minimisation at which point the delocalisation of the Pi electrons became apparent. Two copies of this minimised structure were placed in the same Gaussview window with the distance between the terminal ends of the allyl fragments given as 2.2Å each(2 sig. fig.) Frequency analysis revealed a single imaginary frequency of 818cm^-1, confirming the successful location of the chair transition state.

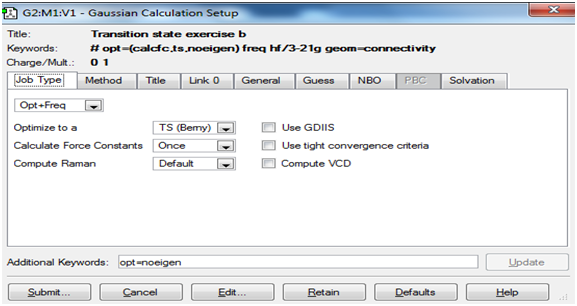
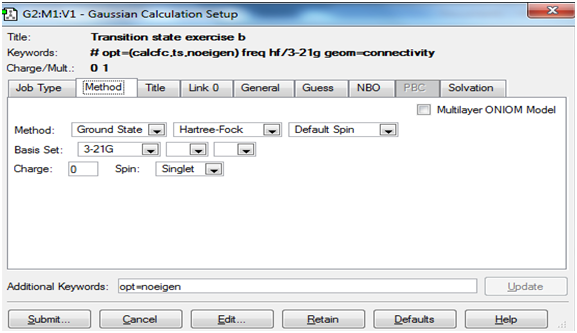
The screenshots below show the 'Job' and 'Method' tabs for setting up the transition state and frequency calculations in Gaussview.

Job tab:

Method tab:

A JMOL link for the HF/3-21G optimised chair transition state is given below:

The LOG file link for the optimisation and frequency calculation is given below:

OPTIMISATIONPLUSFREQUENCYLOGFILE

The Frozen co-ordinate technique: The frozen co-ordinate technique essentially involves two parts.

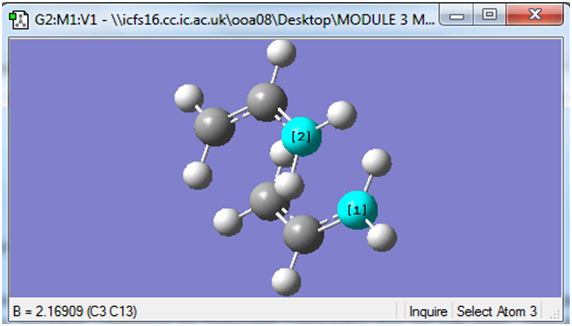
Part 1: Here, based on a guess of which atoms approach each other in the transition state, we set the distance between these atoms to specified value, in this case 2.2Å and optimise the rest of the structure as though carrying out a mimisation.

The screenshot below shows the atoms between which the distances were set to a specified value during the optimisation process.

Note: This procedure was carried out on the other pair of terminal carbons of the allyl fragments.

Below is a link to the LOG file for the output of the minimisation process:

http://hdl.handle.net/10042/to-8047

Part 2: We now carry out the process of optimising the entire output structure to a transition state, and observe, the calculated frequencies. The bonds which had previously been set to a specified value will now be optimised as well by the following procedure:

-Openining the Redundant Coord Editor from the Edit menu.

-Selecting Bond in place of Unidentified and Derivative in place of add(for both previously frozen co-ordinates).

The Job and Method tabs for this calculation are illustrated below:

Job Tab:

Method Tab:

A transition state optimisation was confirmed by the observation of a single imaginary frequency of magnitude 818cm^-1.

The LOG file link for the final output is shown below:

http://hdl.handle.net/10042/to-8050

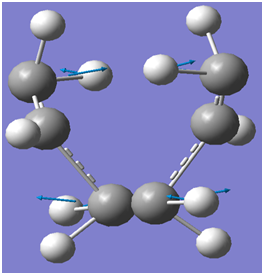
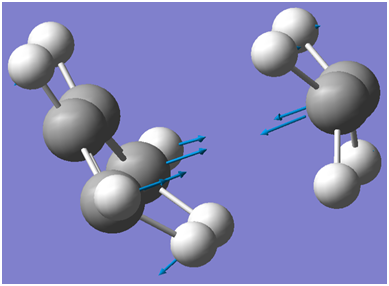
An illustration of the imaginary frequency corresponding to the Cope Rearrangement is shown below:

Optimisation of the boat transition structure: This was carried out based on the QST2 method where the products and reactants were specified and the transition state was determined by interpolation between these two structures. This however requires careful labelling of the atoms of the reactant and product molecules, effectively monitoring where each atom ends up in the product as a result of the re-arrangement.

Procedure for the calculation:

-The checkpoint file corresponding to the optimised 'anti 2' was opened

-The optimised model was copied into a new window, then File-New-Add to MolGroup was specified.

-The reactant molecule was again copied and pasted, this time in window 2.

-The reactant and product molecules could be viewed side by side by making use of the icon showing two molecules side by side.

-Selecting the Labels option under the View menu resulting in numbering of the individual atoms.

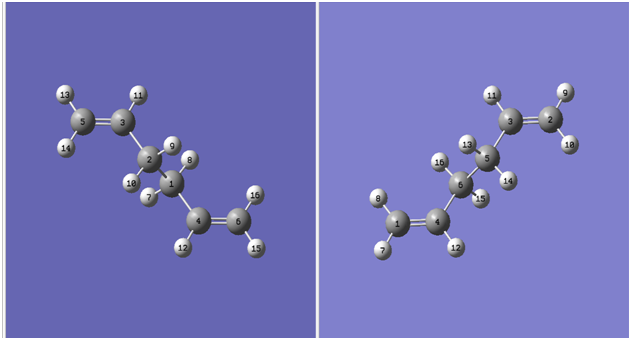
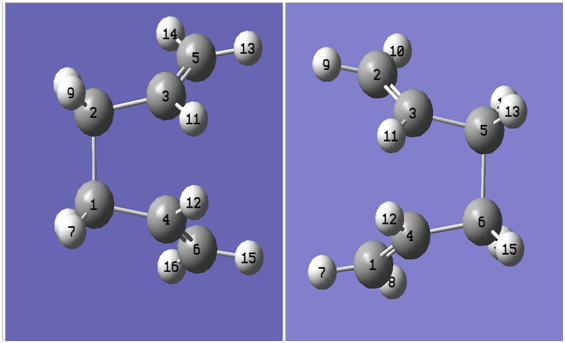
Based on the eventual position of the atoms in the reactant within the product molecule as a result of the Cope rearrangement. The reactant and product molecules were labelled as shown below:

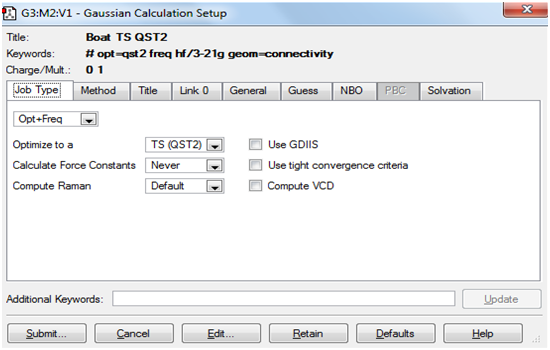
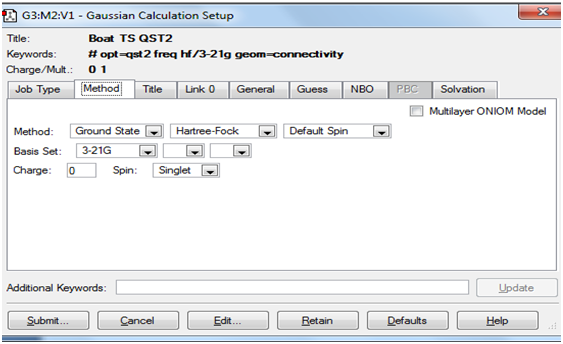
The Screenshots below indicate how the QST2 calculation was set up.

Job tab:

Method tab:

However, the calculation was seen to be unsuccessful as indicated below:

A LOGFILE link of the unsuccessful calculation output is indicated below:

UNSSUCCESSFULOPTIMISATION

Explanation for the failure of the calculation: According to the lab manual, the calculation simply translated the top allyl fragment and did not even consider the possibility of rotation around the central bonds.

The geometries of the reactant and product molecules were then altered as indicated below:

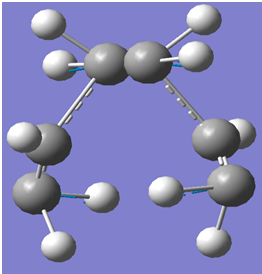
The boat transition state was confirmed by the presence of a single imaginary frequency in the calculation which corresponded to the cope rearrangement.

A screenshot of the boat transition state is indicated below:

A LOG file link for the successful transition state optimisation and frequency calculation is shown below:

OPTIMISATIONPLUSFREQUENCY

An illustration of the cope re-arrangement is illustrated below(based on the imaginary frequency of the boat transition state):

Both the chair and boat transition states were re-optimised using the B3LYP/6-31G(d) level of theory

The D-space link for both optimisations has been given below:

Chair Transition state:http://hdl.handle.net/10042/to-8068

Boat Transition state:http://hdl.handle.net/10042/to-8069

Below is a summary of key results of the computational process

Chair Transition state Density Functional Calculations

Electronic Energy/Hartrees	Sum of electronic and zero point energies/Hartrees at 0K	Sum of electronic and thermal energies/Hartrees at 298.15K
-234.556983	-234.414931	-234.409010

Chair Transition state Hartree Fock Calculations

Electronic Energy/Hartrees	Sum of electronic and zero point energies/Hartrees at 0K	Sum of electronic and thermal energies/Hartrees at 298.15K
-231.619322	-231.466702	-231.461342

Boat Transition state Density Functional Calculations

Electronic Energy/Hartrees	Sum of electronic and zero point energies/Hartrees at 0K	Sum of electronic and thermal energies/Hartrees at 298.15K
-234.543091	-234.402343	-234.396011

Boat Transition state Hartree Fock Calculations

Electronic Energy/Hartrees	Sum of electronic and zero point energies/Hartrees at 0K	Sum of electronic and thermal energies/Hartrees at 298.15K
-231.602802	-231.450927	-231.44298

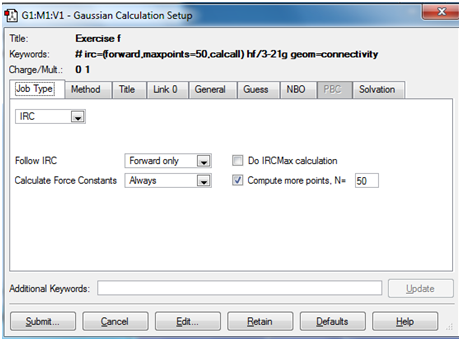
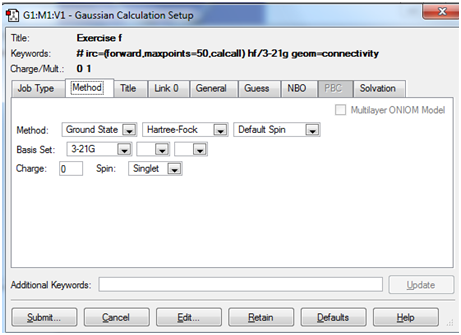
Intrinsic Reaction Co-ordinate Method: The objective here is not to optimise a transition state, but to predict which product is formed from a given transition state. According to the laboratory manual the Intrinsic Reaction Coordinate method generates a series of points by taking small geometry steps in the direction where the slope of the energy surface is steepest.

Here, it was seen that the gauche 2 conformer was generated from the B3LYP optimised transition state. This was done by computing the force constants`at every step of the computation

The Job and Method tabs for this calculation have been illustrated below:

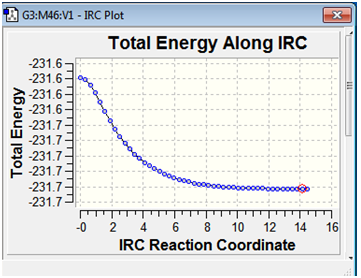
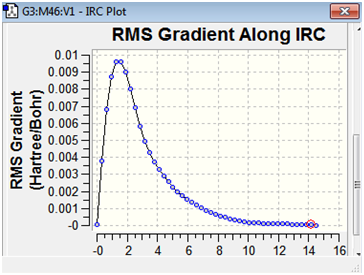
The energy profile along the IRC path suggests that no energy minima have been missed out by selecting the geometries of the final few intermediates along the IRC path for further minimisation.

The variation of energy along the IRC reaction co-ordinate is illustrated below

The RMS gradient along the IRC has also been illustrated below.

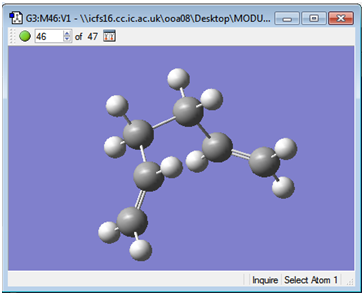
Selection of the intermediate illustrated below and subjection to HF/3-21G minimisation yielded the 'gauche 2' conformation

Below is a D-space link to the files used for the IRC calculation:

http://hdl.handle.net/10042/to-8071

Below is a summary of calculated activation energies:

Chair transition state Hartree Fock Calculations

Temperature/K	Activation energy/kcal/mol
0.00	45.71
298.15	44.70

Chair transition state Density Functional Calculations

Temperature/K	Activation energy/kcal/mol
0.00	34.05
298.15	33.15

The experimental value at 0K is given(lab manual) as 33.5K ± 0.5K. The Density functional calculations agree much better with experiment as expected of a higher level of theory.

Boat transition state Hartree Fock Calculations

Temperature/K	Activation energy/kcal/mol
0.00	55.60
298.15	54.76

Boat transition state Density Functional Calculations

Temperature/K	Activation energy/kcal/mol
0.00	41.95
298.15	41.31

Once again, the Density funtional calculations are in better agreement with the experimental value of 44.7 ± 2.0K at 0K. Based on the above results, it can be predicted that the reaction proceeds more slowly via a boat transition state. It was also noted that the overall accuracy of the calculations seems to be lower in the case of the boat transition state calculation. The relative stability of the chair transition state may be explained using secondary orbital interactions.

The Diels Alder Cycloaddition

The reaction between cis butadiene and ethene: The Diels Alder reaction is a pericyclic reaction in which the π orbitals of the dienophile are used to form new σ bonds with the π orbitals of the diene. According to the lab manual, the reaction may occur in a concerted stereospecific reaction if the HOMO of one reactant can interact with the LUMO of another reactant(in which case the interacting orbitals have the same symmetry properties and there is significant overlap density).

A good starting point therefore is to consider the HOMO and LUMO of cis butadiene as well as the HOMO and LUMO of ethene.

Note: Models were optimised and molecular orbitals visualised using the B3LYP/6-31G(d) method.

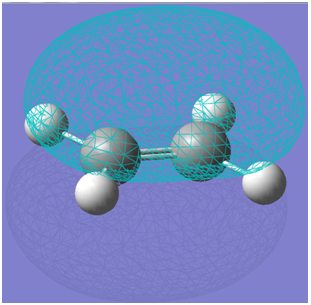
The HOMO of ethene is visualised below.

The LUMO of ethene is visualised below.

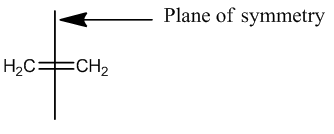
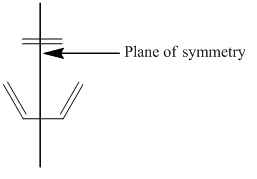
It can be seen that the HOMO is symmetric with regard to the plane of symmetry while the LUMO is antisymmetric with regard to the plane of symmetry. The plane of symmetry of interest is indicated below:

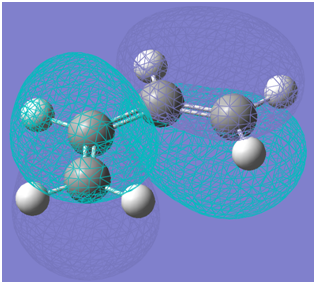
The HOMO of cis-butadiene is visualised below:

The LUMO of cis-butadiene is visualised below:

It can be seen that the HOMO is antisymmetric with respect to the plane of symmetry while the LUMO is symmetric with respect to the plane of symmetry. The plane of symmetry of interest is indicated below:

Given these symmetry considerations it is therefore conceivable that the HOMO of ethene may interact with the LUMO of cis-butadiene and that the HOMO of cis-butadiene may interact with the LUMO of ethene.

Transition state optimisation for this reaction was successfully carried out.

A link to the optimised transition state model is given below

http://hdl.handle.net/10042/to-8058

The geometry of the transition state structure is shown in the screenshot below:

A JMOL link for the transition state structure has also been included.

The length of the partly formed sigma C-C bond lengths was measured as 2.27Å. According to the literature, the Van der Waals radius of a carbon atom is 1.70Å, while typical C-C bonds(sp³) are 1.54Å in length, while a typical C=C bond(sp²) measures 1.34Å. We can conclude from this data that the Van der Waals radii of the carbon atoms has been penetrated within the transition state, indicating that there is some sharing of electron density and that a reaction is taking place. However, the length of the partially formed bond within the transition state is considerably less than that of an sp³ or sp² carbon-carbon bond, indicating that the interaction has not yet reached a stable minimum, which is reasonable given that a transition state is under examination.

Below is an illustration of the vibration that corresponds to the reaction path at the transition state. It can be seen that the formation of the two new C-C bonds is synchronous.

The lowest positive frequency clearly does not allow for synchronous formation of two new sigma bonds as it does not allow for simultaneous sigma orbital overlap between the p orbitals of the terminal carbon atoms of cis-butadiene and ethene.

Below is a link to the LOG and checkpoint files in order to visualise the vibrations:

http://hdl.handle.net/10042/to-8058

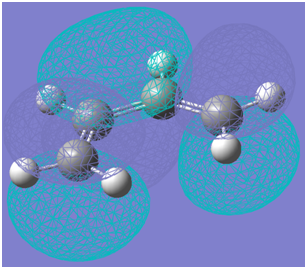
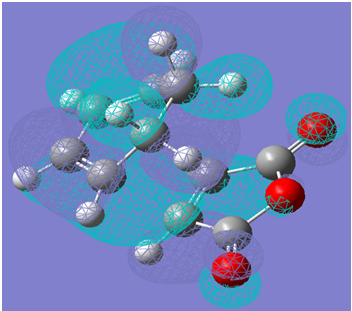
The HOMO of the transition structure is illustrated below:

The HOMO of the transition structure is symmetric with respect to the plane of symmetry illustrated below:

Therefore, by symmetry considerations, the HOMO of the transition structure was likely formed by the HOMO of ethylene and the LUMO of cis-butadiene. Therefore, as the HOMO of one reactant can interact with the LUMO of the other due to the presence of significant overlap density as a result of the similarity of their symmetry properties, the reaction may occur in a concerted stereospecific fashion as suggested by the transition state imaginary vibration.

The reaction of cyclohexa-1,3-diene with maleic anhydride

The aim of this exercise is to study the regioselectivity of the above reaction.

Using the B3LYP/6-31G(d) method, a transition state optimisation and frequency calculation was successfully carried out for the endo transition state.

A link to the output files for this calculation has been indicated below:

http://hdl.handle.net/10042/to-8111

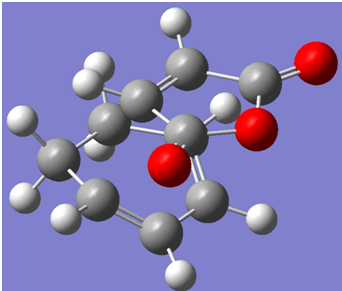
Below is a screenshot of the endo-transition state.

A JMOL link to the transition state structure has been indicated below:

The electronic energy of the endo transition state structure was calculated to be -612.683396 a.u

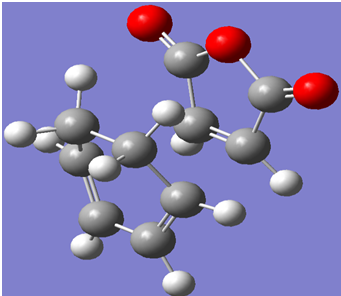
A screenshot of the exo-transition state calculated using the same method, along with a JMOL link have been indicated below:

The link to the input and output files for this calculation is:http://hdl.handle.net/10042/to-8112

The electronic energy of the exo transition state structure was calculated to be -612.679311 a.u.

These calculated energies confirm a known experimental fact about the endo product of the Diels-Alder reaction, that it is the kinetic product of the reaction. This can be deduced given that the endo-transition state is lower in energy. The exo transition state is potentially more strained given the eclipse of the -(C=O)-O-(C=O)- fragment in the anhydride ring by two sp³ carbons in the exo transition state as opposed to two sp² carbons in the endo transition state.

It is also noteworthy that substituents possessing pi orbitals that can interact with the new double bond that is being formed in the product may stabilise the regiochemistry of the reaction.

Secondary orbital effects will now be studied within the reaction.

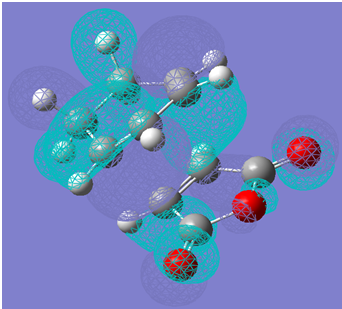
First, a screen shot of the HOMO of the endo transition state is shown below.

A link to the checkpoint file used to visualise this HOMO is given below.

http://hdl.handle.net/10042/to-8066

The HOMO of the exo transition state has been visualised below:

A link to the checkpoint file used for the visualisation process is indicated below:

http://hdl.handle.net/10042/to-8067

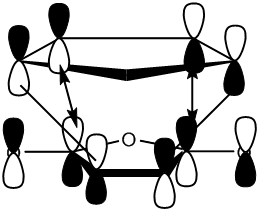
According to the reference there is a stabilising interaction interaction between the carbonyl groups and the newly forming pi bond within the endo transition state which stabilises the endo transition state with respect to the exo transition state.

This stabilising interaction is better visualised by observing the LUMO of the endo transition state.

This is consistent with the Frontier Orbital Picture suggested by the reference and illustrated below:

Primary interactions are illustrated with double headed arrows, while secondary interactions are illustrated with black lines that have no arrowheads.

Such a stabilising interaction is not possible within the exo transition state due to it's geometry.

Thus it can be concluded that secondary orbital interactions contribute to the stabilisation of the endo transition state relative to the exo transition state.

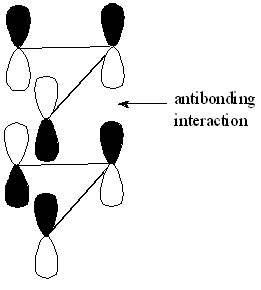
These secondary orbital interactions also provide a means of explaining the relative stability of the chair transition state in Cope re-arrangement studied earlier.

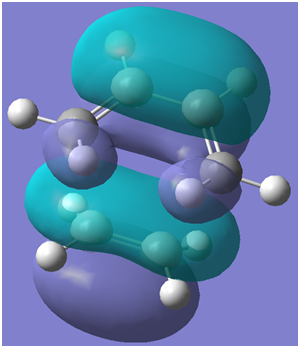
This is illustrated below:

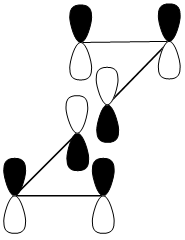
This unfavourable antibonding interaction, seen in the boat transition state is absent in the chair transition state as illustrated

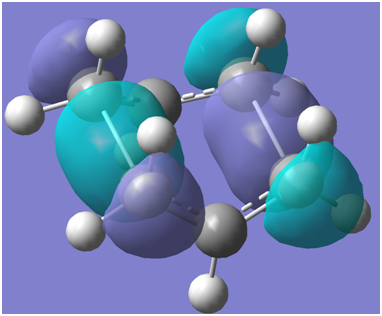
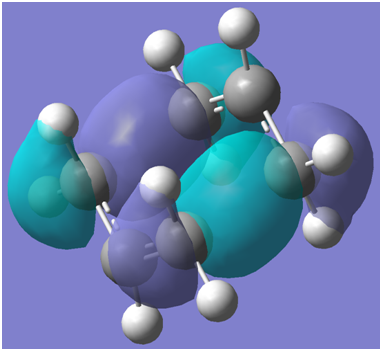
These interactions may be correlated to the following calculated HOMO-1 plots

Boat:

Chair:

The output files confirm that the chair HOMO-1 is lower in energy than the boat HOMO-1 structure. Chair HOMO-1 visualisation link: http://hdl.handle.net/10042/to-8176 Boat HOMO-1 visualisation link:http://hdl.handle.net/10042/to-8177

It is worth noting however, that these calculations have not taken solvent effects into account.

Note on calculations:

Cis butadiene and ethene were initially optimised using the AM1 semi empirical molecular orbital method.

Cis butadiene LOG FILE:OPTIMISATIONLOGFILE

Ethene LOG FILE: OPTIMISATIONLOGFILE

Cis butadiene was optimised using DFT B3LYP/6-31G(d)

Cis butadiene LOG FILE:OPTIMISATIONLOGFILE

Frequency calculations were carried out on the cis-butadiene models to ensure successful optimisation had occurred.

Cis butadiene frequency calculation link:FREQUENCYLOGFILE

The transition state for the reaction between cis-butadiene and ethene was located using the frozen-co-ordinate tachnique.

The same procedure was used in the computational process for the reaction between maleic anhydride and cyclopentadiene.

Maleic anhydride AM1 optimisation link:OPTIMISATIONLOGFILE

Maleic anhydride DFT optimisation link:OPTIMISATIONLOGFILE

Maleic anhydride frequency analysis link:FREQUENCYLOGFILE

Cyclopentadiene AM1 optimisation link:OPTIMISATIONLOGFILE

Cyclopentadiene DFT optimisation link:OPTIMISATIONLOGFILE

Cyclopentadiene frequency analysis link:FREQUENCYLOGFILE