Rep:MOD:KVM125133
Week 1
EX3 Optimisation
Three molecules with EX3 were generated in GaussView and optimised using various methods and basis sets. The calculated bond lengths and angles of the optimised molecules were then compared. The optimisation calculation involves making slightly adjustments to the nuclear positions in order to lower the total energy of the molecule. Only the nuclei are adjusted because the electrons are considered to adjust their positions instantaneously with the movement of the larger, heavier nuclei (Born-Oppenheimer approximation). The optimisation is complete once the global energy minimum for the molecule has been found.
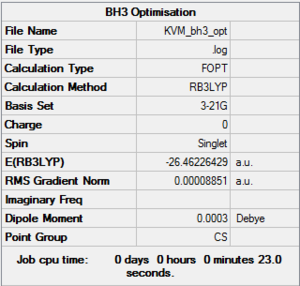
BH3:B3LYP/3-21G
A molecule of BH3 was generated in GaussView. The three B-H bonds were set to different lengths to break the symmetry of the molecule: 1.53 Å, 1.54 Å and 1.55 Å. The molecule was optimised in Gaussian using the B3LYP method and 3-21G basis set. The results from the optimisation are given below.
Optimisation file: here
The point group symmetry of the optimised molecule is not D3h as was expected. This is because by setting the initial bond lengths to different values, the rotational symmetry of the molecule was broken. The optimised molecule has slightly different B-H bond lengths for each bond, with differences at the 4th decimal place.
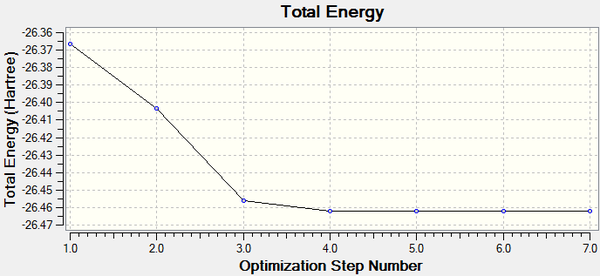
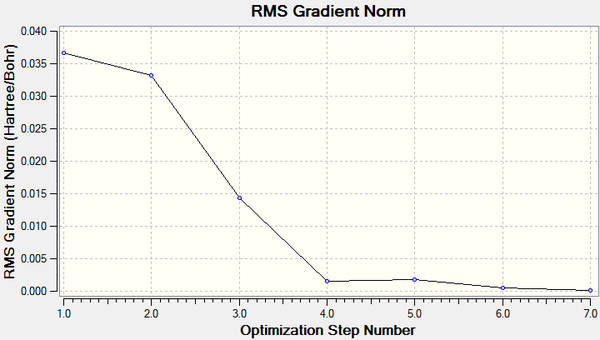
The change in total energy and RMS gradient during the optimisation are shown below. The final structure has the most negative total energy and smallest gradient of the steps.
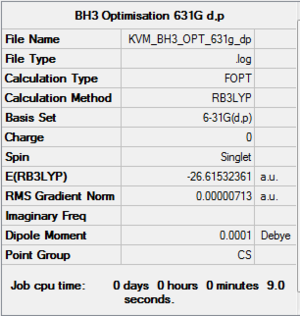
BH3:B3LYP/6-31G(d,p)
The optimised structure of BH3 was re-optimised using the same method with a higher level basis set: 6-31G(d,p). Higher level basis sets use fewer approximations and therefore deliver better results, but require more computing power and time.
Optimisation file: here
| summary data | convergence | Jmol | |||
|---|---|---|---|---|---|
|
Item Value Threshold Converged? Maximum Force 0.000012 0.000450 YES RMS Force 0.000008 0.000300 YES Maximum Displacement 0.000063 0.001800 YES RMS Displacement 0.000039 0.001200 YES |
|
The molecule still does not have the expected D3h symmetry due to minor differences in the bond lengths and angles.
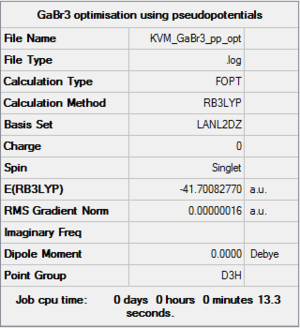
GaBr3:B3LYP/LANL2DZ
A molecule of GaBr3 was generated in GaussView. The symmetry of the molecule was constrained to the D3h point group with very tight tolerance. A medium level basis set (LanL2DZ) was chosen for the optimisation and the same B3LYP method used. The higher level basis set was required for this optimisation because Ga and Br are both third row heavy atoms. The Lan2DZ basis set uses pseudo-potentials on heavy elements. This means the core electrons are assumed not to be involved in bonding and so are using a pseudo-potential function.
optimisation file: DOI:10042/195134
| summary data | convergence | Jmol | |||
|---|---|---|---|---|---|
|
Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000003 0.001800 YES RMS Displacement 0.000002 0.001200 YES |
|
The summary data and results file indicate that the optimisation was successful. The symmetry was constrained prior to optimisation so the molecule belongs to the D3h point group.
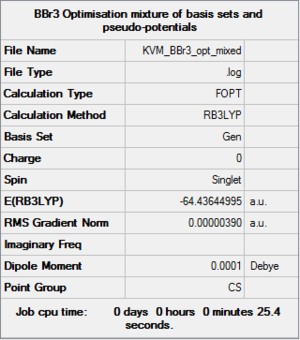
BBr3:B3LYP/6-31G(d,p)LANL2DZ
The optimised BH3 molecule was modified to give a BBr3 molecule by replacing the H atoms with Br atoms. This molecule was then optimised using a mixture of basis-sets and pseudo-potentials because it contains a mixture of light and heavy atoms. Pseudo-potentials should only be used to model heavy atoms, so the 6-31G(d,p) basis set was used for the light B atom, and LanL2DZ pseudo-potentials for the heavy Br atoms.
optimisation file: DOI:10042/195143
| summary data | convergence | Jmol | |||
|---|---|---|---|---|---|
|
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000035 0.001800 YES RMS Displacement 0.000024 0.001200 YES |
|
The summary data and convergence indicate that the optimisation was successful. The symmetry had not been constrained prior to optimisation so the minor differences in bond lengths and angles mean that the final molecule has not been assigned D3h symmetry.
Geometry Comparison
| BH3 | GaBr3 | BBr3 | |
|---|---|---|---|
| r(E-X) Å | 1.19 | 2.35 | 1.93 |
| θ(X-E-X) degrees(º) | 120.0 | 120.0 | 120.0 |
Changing the ligand from H to Br increases the bond length from 1.19 Å to 1.93 Å. H and Br both form a single σ bond to B so the difference is not due to bond order. Bromine has an atomic radius of 94 pm, while Hydrogen is much smaller with a radius of 53 pm. This accounts for part of the increase in bond length but not all.
Hydrogen and Bromine bond through different valence atomic orbitals. H bonds through its 1s orbital which is compact and close to the nucleus. Br bonds through the much larger and more diffuse 4p orbital. The central Boron atom also has small, dense valence orbitals and therefore has better overlap with Hydrogen than with Bromine.
Boron has a Pauling electronegativity of 2.04, Hydrogen of 2.20 and Bromine of 2.96. A larger electronegativity difference makes the bond more ionic than covalent in nature and increases the bond strength. This would be expected to shorten the B-Br bond length but the orbital overlap and atomic radius effects override any electronegativity difference.
Changing the central element also change the bond length. Ga and B are both group 13 elements but Ga is further down the group and therefore its valence electrons reside in larger, more diffuse orbitals. Ga and Br are both in the same row so their orbital overlap is better than that of B with Br. Ga and Br also have a large electronegativity difference (Ga has a Pauling electronegativity of 1.81). Ga has an atomic radius of 130 pm and therefore still forms longer bonds to Br than B with an atomic radius of 85 pm.
A bond is a force of attraction between two or more atoms, involving the sharing or transfer of electrons between them. In covalent bonds the negatively charged electrons have an attractive electrostatic interaction with the nuclei of both their own and the other atom. Formation of the bond lowers the total energy of the system. A certain amount of energy is released upon formation of the bond and is required to break the bond. Bonds drawn as a line between two atoms do not always provide an accurate description of bonding in a molecule, because orbital mixing in molecular orbitals generates lobes of electron density in phase or out of phase with one another. In phase overlap of electron density creates bonding interactions between atoms, which are often simplified to 2-centre-2-electron bonds when most of the electron density lies along the axis between the two atoms.
An example of strong bond is the triple bond in N2 which has a bond energy of 941 kJ/mol. Single bonds are much weaker than triple bonds: an example of weak bond is the N-N single bond which has an energy of only 160 kJ/mol. C-C bonds can be classified as medium, with an average bond energy of 347 kJ/mol.
GaussView draws bonds based on the distance between two atoms. If the distance is consistent with a particular bond order, the relevant bond will be drawn. It does not take into account attractive interactions between the two atoms. If two atoms are further than would be expected for a bond to form, GaussView will not draw a bond between them.
Frequency Analysis
Frequency analysis can be used to confirm that the optimised structure is a minimum. If so, all frequencies should be positive. If there is one negative frequency, the structure is a transition state and if there are multiple the calculation has not completed correctly.
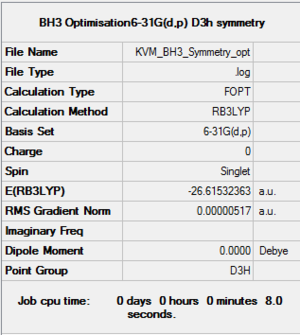
BH3: B3LYP/6-31G(d,p)
The molecule was constrained to D3h symmetry then optimised at the B3LYP/6-31G(d,p) level.
Optimisation file: here
| summary data | convergence | Jmol | |||
|---|---|---|---|---|---|
|
Item Value Threshold Converged? Maximum Force 0.000220 0.000450 YES RMS Force 0.000106 0.000300 YES Maximum Displacement 0.000709 0.001800 YES RMS Displacement 0.000447 0.001200 YES |
|
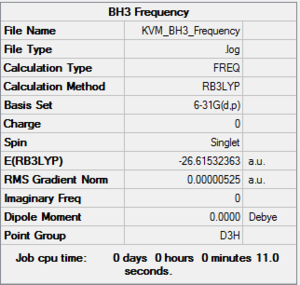
The frequency calculation was then carried out on the optimised molecule using the same method and basis set.
Frequency file: here
| summary data | low modes |
|---|---|
|
Low frequencies --- -4.8294 -1.2074 -0.0055 1.0243 9.1094 9.1890 Low frequencies --- 1162.9789 1213.1709 1213.1736 |
The motions of the centre of mass of the molecule, listed in the top row of the table above are all within the ±15 cm-1 range. As expected, they are much smaller than the frequencies of the first vibrations, listed in the second row. All vibrational frequencies are positive so the optimisation to a minimum was successful.
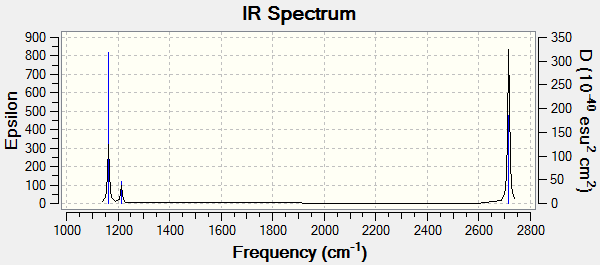
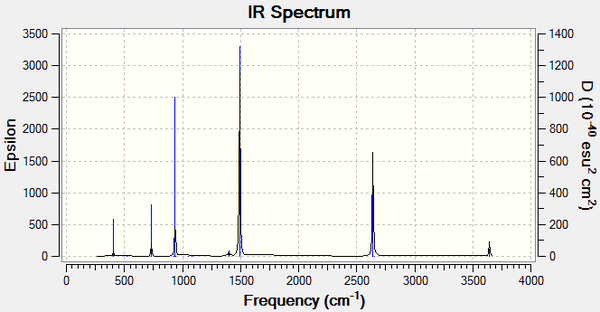
Vibrational spectrum for BH3
The frequency analysis also computes the vibrations of the molecule. The frequencies, intensities and nature of the 6 vibrations of BH3 are listed below.
| wavenumber (cm-1) | Intensity | IR active? | type |
| 1163 | 93 | yes | bend |
| 1213 | 14 | very slight | bend |
| 1213 | 14 | very slight | bend |
| 2582 | 0 | no | stretch |
| 2716 | 126 | yes | stretch |
| 2716 | 126 | yes | stretch |
One of the six vibrations has zero intensity and will not be observed on the spectrum. This is because the vibration does not change the dipole moment of the molecule, so it is IR inactive. Degenerate vibrations will appear as single peaks with a higher intensity so the two stretches at 2716 cm-1 appear as one peak, as do the two degenerate bends at 1213 cm-1. Only three peaks are therefore observed on the spectrum despite the six different vibrations of the molecule.
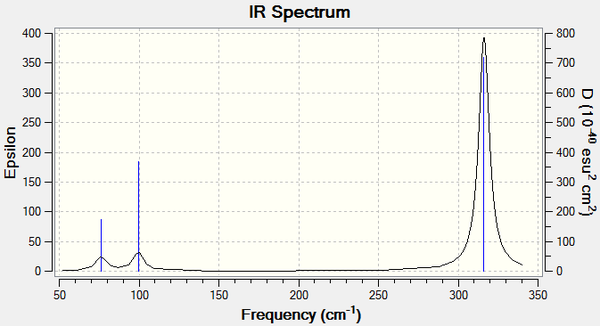
GaBr3: B3LYP/LANL2DZ
The frequency analysis was carried out on the molecule optimised earlier, continuing to use the LanL2DZ basis set.
Frequency file: DOI:10042/195151
| summary data | low modes |
|---|---|

|
Low frequencies --- -1.4878 -0.0015 -0.0002 0.0096 0.6540 0.6540 Low frequencies --- 76.3920 76.3924 99.6767 |
Despite constraining the molecule to D3h symmetry in the optimisation, the summary of the frequency calculation show the point group of the molecule as C3h. The low frequencies are nonetheless still in the expected range and the vibrational frequencies are all positive, confirming the optimisation has reached a minimum.
Vibrational spectrum for GaBr3
| wavenumber (cm-1) | Intensity | IR active? | type |
| 76 | 3 | very slight | bend |
| 76 | 3 | very slight | bend |
| 100 | 9 | no | bend |
| 197 | 0 | no | stretch |
| 316 | 57 | yes | stretch |
| 316 | 57 | yes | stretch |
Both molecules have D3h symmetry and 3N-6=6 vibrational modes, 3 bends and 3 stretches. The frequencies of the vibrations are much higher in BH3 than GaBr3. This is because vibrational frequency ν is related to both bond strength k and the reduced mass μ.
ν = (k/μ)1/2
Since Ga and Br are much heavier than B and H, the reduced mass of Ga-Br is much larger than that of B-H. The frequencies of the GaBr3 vibrational modes are therefore much lower than those of BH3. The intensities of the modes also vary between the two molecules. Overall, the intensities are lower in the GaBr3 molecule.
The modes are also reordered. In GaBr3 the lowest vibrational frequency corresponds to two degenerate in-plane bending motions that involve displacement of all four constituent atoms. The next-lowest frequency is the out-of-plane bend. In BH3 these degenerate motions have a higher frequency than the out-of-plane bend and do not involve movement of the central B atom. The three stretches occur in the same order for the two molecules. No difference between the two is observed for the zero-intensity IR-inactive stretch. For the degenerate stretches, the H atoms show the greatest displacement in BH3 whereas the Ga atom moves the most in GaBr3.
The reordering of the frequencies and change in motion is explained by the difference in relative masses between the atoms of the molecule. A B atom is approximately 10 times as heavy as a H atom, whereas Br is 1.15 times heavier than the central Ga atom. The result of this discrepancy is minimal movement of the central B atom because the light H atoms are easily displaced, and greater movement of the central Ga atom because it is moved as easily as the outer Br atoms. This is apparent in the A2" umbrella motion, which has the lowest frequency vibration in BH3 but the third-lowest in GaBr3. In the former, the central B has no displacement vector, whilst in the latter the central Ga has a larger displacement vector than the Br atoms.
The method and basis set chosen will use a number of approximations in the calculation. These approximations must be consistent across the optimisation and frequency calculations or the accuracy of the results would be compromised.
The frequency analysis serves two main purposes. It calculates IR and Raman modes that can be compared with experimental data to verify the accuracy of the model. It can also be used to confirm that the optimisation has reached a minimum structure, in which case all frequencies will be positive. A single negative frequency is indicative of optimisation to a transition state, and multiple indicate the optimisation has failed.
The first row of low frequencies represent the motions of the centre of mass of the molecules, of which there are three translational and three rotational. These six motions can be thought of as the -6 term in 3N-6, the number of vibrational modes of a non-linear molecule. The frequencies are closer to zero for better computational methods. The frequency analysis can therefore also show the quality of the optimisation method.
Molecular Orbitals of BH3
Calculations were carried out on the .chk file of the optimised BH3 to give computed molecular orbitals. This was done as an energy calculation using the B3LYP method and 6-31G(d,P) basis set.
File: DOI:10042/195152
The diagram below shows the molecular orbitals derived from LCAO as well as the occupied and the lowest few unoccupied molecular orbitals calculated above.
The real and LCAO molecular orbitals are in good agreement in both ordering and shape. The lowest energy orbital is the 1a1 but it is too low in energy to be involved in mixing and not shown on this diagram. The 2a1' MO is all-bonding and next-lowest in energy. The HOMO is in both cases the doubly degenerate 1e' with in-phase overlap between the B and H3 fragments. The LUMO is the non-bonding 1a2". Qualitative MO theory therefore accurately predicts the shape and ordering of molecular orbitals in simple molecules such as BH3.
The relative ordering of the 3a' and 2e' are difficult to evaluate using qualitative theory because s-s interactions are stronger than s-p, which would lead to the 3a' being higher in energy. However, the a1' are lower than e' which would make the 3a1' lower. Energy calculations show that the 3a1' is lower in energy. Qualitative MO theory does therefore have some limitations.
NBO Analysis of NH3
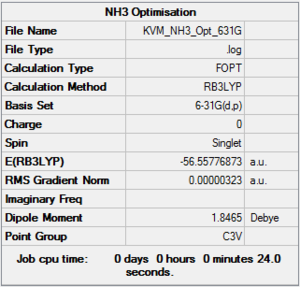
Optimisation of NH3:B3LYP/6-31G(d,p)
A molecule of NH3 was created and optimised using the B3LYP method and 6-31G(d,p) basis set.
Optimisation file: here
| summary data | convergence | Jmol | |||
|---|---|---|---|---|---|
|
Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000012 0.001800 YES RMS Displacement 0.000008 0.001200 YES |
|
The optimisation has converged to a minimum. The optimised molecule has the expected C3v symmetry despite not having been constrained prior to optimisation. The bond angles are 105.7° and the N-H bond lengths are 1.02 Å.
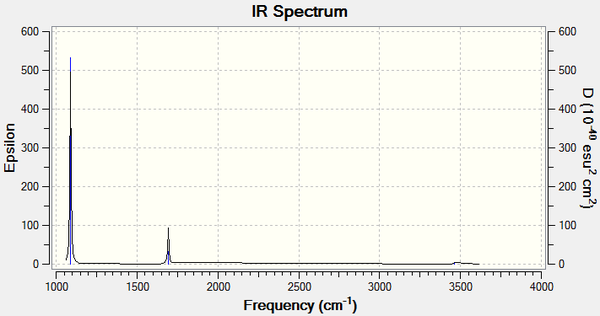
Frequency NH3:B3LYP/6-31G(d,p)
A frequency calculation was carried out on the optimised molecule using the same method and basis set. The point group was constrained to C3v.
Frequency file: here
| summary data | low modes |
|---|---|
|
Low frequencies --- -0.0130 -0.0016 0.0014 7.0747 8.1044 8.1047 Low frequencies --- 1089.3849 1693.9369 1693.9369 |
The low frequencies are within an acceptable range and the vibrational frequencies are all positive. C3v symmetry has been preserved.
Vibrational spectrum for NH3
| wavenumber (cm-1) | Intensity | IR active? | type |
| 1089 | 145 | yes | bend |
| 1694 | 14 | very slight | bend |
| 1694 | 14 | very slight | bend |
| 3462 | 1 | no | stretch |
| 3590 | 0 | no | stretch |
| 3590 | 0 | no | stretch |
Charge Distribution of NH3

A population analysis was carried out on the NH3 molecule, still using the B3LYP method and 6-31G(d,p) basis set. The charge distribution of the molecule was viewed over the range -1.125 (bright red) to +1.125 (bright green). The N atom carries a charge of -1.125 and each H atom a charge of +0.375.
This can be seen in the summary of natural population analysis:
Summary of Natural Population Analysis:
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
N 1 -1.12514 1.99982 6.11104 0.01429 8.12514
H 2 0.37505 0.00000 0.62249 0.00246 0.62495
H 3 0.37505 0.00000 0.62250 0.00246 0.62495
H 4 0.37505 0.00000 0.62250 0.00246 0.62495
=======================================================================
* Total * 0.00000 1.99982 7.97852 0.02166 10.00000
The orbital occupancies, types and hybridisation can all be determined using an NBO analysis. The table below shows the 5 occupied orbitals. The first three are NH bonds. They all have 2 electron occupancy, of which 69% of the electron density is contributed by N and 31% byH. The N orbitals involved are sp3 hydridised while the H orbital is s. The fourth is a core orbital on N with 100% s character: it is the 1s atomic orbital. The fifth is sp3 hybridised but localised entirely on N: it is the nitrogen lone pair.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.99909) BD ( 1) N 1 - H 2
( 68.83%) 0.8297* N 1 s( 24.87%)p 3.02( 75.05%)d 0.00( 0.09%)
-0.0001 -0.4986 -0.0059 0.0000 0.8155
0.0277 0.2909 -0.0052 0.0000 0.0000
-0.0281 0.0000 0.0000 -0.0032 0.0082
( 31.17%) 0.5583* H 2 s( 99.91%)p 0.00( 0.09%)
-0.9996 0.0000 -0.0289 -0.0072 0.0000
2. (1.99909) BD ( 1) N 1 - H 3
( 68.83%) 0.8297* N 1 s( 24.87%)p 3.02( 75.05%)d 0.00( 0.09%)
0.0001 0.4986 0.0059 0.0000 0.4077
0.0138 -0.2909 0.0052 0.7062 0.0240
-0.0140 0.0076 -0.0243 -0.0033 0.0031
( 31.17%) 0.5583* H 3 s( 99.91%)p 0.00( 0.09%)
0.9996 0.0000 -0.0145 0.0072 -0.0250
3. (1.99909) BD ( 1) N 1 - H 4
( 68.83%) 0.8297* N 1 s( 24.87%)p 3.02( 75.05%)d 0.00( 0.09%)
0.0001 0.4986 0.0059 0.0000 0.4077
0.0138 -0.2909 0.0052 -0.7062 -0.0240
-0.0140 -0.0076 0.0243 -0.0033 0.0031
( 31.17%) 0.5583* H 4 s( 99.91%)p 0.00( 0.09%)
0.9996 0.0000 -0.0145 0.0072 0.0250
4. (1.99982) CR ( 1) N 1 s(100.00%)
1.0000 -0.0002 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.0000 0.0000
5. (1.99721) LP ( 1) N 1 s( 25.38%)p 2.94( 74.53%)d 0.00( 0.10%)
0.0001 0.5036 -0.0120 0.0000 0.0000
0.0000 0.8618 -0.0505 0.0000 0.0000
0.0000 0.0000
The summary of occupied NBOs and their energies is in the table below. It shows that all N-H bonds are of equal energy. The core orbital is much lower in energy than the bonding orbitals formed from valence atomic orbitals. The lone pair is higher in energy than the bonding orbitals.
The molecule has a pyramidal structure not trigonal planar as in BH3 because of the lone pair on nitrogen occupying a fourth place in nitrogen's coordination sphere. The H-N-H angle is smaller than the normal tetrahedral angle of 109.5° because of electron-electron repulsion between the lone pair and the N-H bonds.
Principal Delocalizations
NBO Occupancy Energy (geminal,vicinal,remote)
====================================================================================
Molecular unit 1 (H3N)
1. BD ( 1) N 1 - H 2 1.99909 -0.60417
2. BD ( 1) N 1 - H 3 1.99909 -0.60419
3. BD ( 1) N 1 - H 4 1.99909 -0.60419
4. CR ( 1) N 1 1.99982 -14.16767
5. LP ( 1) N 1 1.99721 -0.31754
Association Energies: Ammonia-Borane
Optimisation of NH3BH3:B3LYP/6-31G(d,p)
A molecule of NH3BH3 was created and optimised using the B3LYP method and 6-31G(d,p) basis set.
Optimisation file: here
| summary data | convergence | Jmol | |||
|---|---|---|---|---|---|
|
Item Value Threshold Converged? Maximum Force 0.000001 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000016 0.000060 YES RMS Displacement 0.000007 0.000040 YES |
|
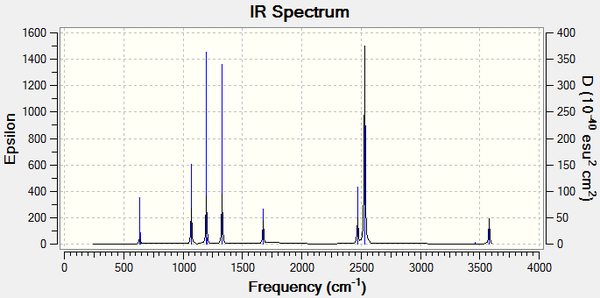
Frequency NH3BH3:B3LYP/6-31G(d,p)
A frequency calculation was carried out on the optimised molecule using the same method and basis set.
Frequency file: here
| summary data | low modes |
|---|---|
|
Low frequencies --- -2.3896 -0.0014 0.0006 0.0011 0.6433 5.2753 Low frequencies --- 263.4745 632.9579 638.4357 |
Vibrational Frequencies
| wavenumber (cm-1) | Intensity | IR active? | type |
| 266 | 0 | no | bend |
| 632 | 14 | very slight | stretch |
| 639 | 4 | very slight | bend |
| 639 | 4 | very slight | bend |
| 1069 | 40 | slight | bend |
| 1069 | 40 | slight | bend |
| 1196 | 109 | yes | bend |
| 1204 | 3 | very slight | bend |
| 1204 | 3 | very slight | bend |
| 1329 | 114 | yes | bend |
| 1676 | 28 | slight | bend |
| 1676 | 28 | slight | bend |
| 2470 | 67 | yes | stretch |
| 2530 | 231 | yes | stretch |
| 2530 | 231 | yes | stretch |
| 3463 | 3 | very slight | stretch |
| 3579 | 28 | slight | stretch |
| 3580 | 28 | slight | stretch |
Association Energy
All energies are total energies computed using the B3LYP method and 6-31G(d,p) basis set.
E(BH3) = -26.6153236 a.u.
E(NH3) = -56.5577687 a.u.
E(NH3BH3) = -83.2246889 a.u.
The energy of association is equal to the difference between the energy of the NH3BH3 acid base pair and that of the NH3 and BH3 on their own.
ΔE=E(NH3BH3)-[E(NH3)+E(BH3)]
ΔE= -0.0515966 a.u.
ΔE= -135.45 kJ/mol
The dative bond form upon association of NH3 and BH3 can be classified as a weak bond. Little energy input is required to dissociate the NH3BH3 adduct into NH3 and BH3.
Week 2: Aromaticity Project
Benzene
Optimisation & Frequency Analysis
A molecule of benzene was generated in GaussView and optimised using the D3LYP method and 6-31G(d,p) basis set with tight convergence. The symmetry was constrained to D6h.
Optimisation file: here
| summary data | convergence | Jmol | |||
|---|---|---|---|---|---|
|
Item Value Threshold Converged? Maximum Force 0.000001 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000001 0.000060 YES RMS Displacement 0.000000 0.000040 YES |
|
The frequency calculation was run on the optimised molecule. The low frequencies are within the acceptable range and the vibrational frequencies are all positive, indicating the optimisation to a minimum was successful.
Frequency file: here
| summary data | low modes |
|---|---|
|
Low frequencies --- -10.2549 -5.6651 -5.6651 -0.0056 -0.0056 -0.0008 Low frequencies --- 414.5451 414.5451 621.0429 |
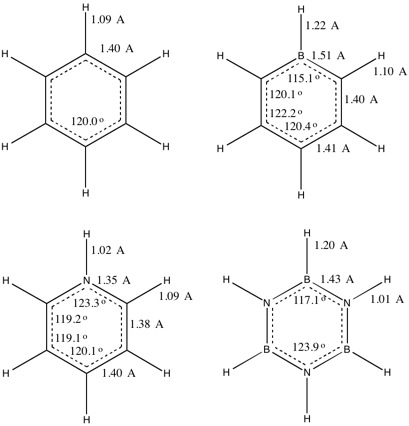
The Jmol files above show bonding in benzene as localised single and double bonds. The results file, however, shows equal bond lengths for all the C-C bonds (1.40 Å) and equal bond angles for all C-C and C-H bonds (120.0°) indicating delocalised double bonding, as would be expected in an aromatic ring. The bond length is intermediate between single C-C bonds at 1.54 Å and double bonds at 1.34 Å and matches the experimental value of 1.40 Å.
There are 3N-6 = 30 vibrational modes of which only 7 are IR active. There are 3 pairs of degenerate modes, so only 4 peaks are observed on the vibrational spectrum. Benzene is a highly symmetric molecule, so many of its vibrational modes do not involve a change in dipole moment and are IR inactive.
NBO Analysis
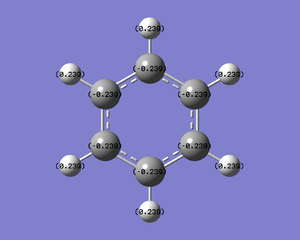
An energy calculation was run on the optimised molecule. The charge distribution shows carbon atoms with a charge of -0.239 and hydrogens with a charge of +0.239.
NBO file here
| Details | Charge Distribution | Charge Values |
|---|---|---|
|

|
|
Orbital 1 shown below is a σ bonding orbital between two carbon atoms. 35% s and 65 % p contribution indicate that the bond is formed from two sp2 hybridised orbitals. The bond is heteronuclear and therefore has equal electron contributions from each atom. The occupancy is 1.98, sufficiently close to 2 to indicate a 2-centre-2-electron bond. All six carbon atoms are linked by these bonding orbitals.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.98098) BD ( 1) C 1 - C 2
( 50.00%) 0.7071* C 1 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 0.7063
0.0300 -0.3840 0.0193 0.0000 0.0000
-0.0151 0.0000 0.0000 0.0069 -0.0109
( 50.00%) 0.7071* C 2 s( 35.20%)p 1.84( 64.76%)d 0.00( 0.04%)
-0.0001 0.5932 -0.0079 0.0006 -0.6857
0.0017 0.4197 0.0357 0.0000 0.0000
-0.0135 0.0000 0.0000 0.0096 -0.0109
Orbital 2 is a π bonding orbital between two carbon atoms. It is formed entirely from p orbitals with equal contribution from each atom. The occupancy is 1.66. Six π electrons are delocalised over six atoms, so an occupancy of 1 per C-C bond would be expected. The higher value is due to higher electron density in the aromatic π cloud.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
2. (1.66514) BD ( 2) C 1 - C 2
( 50.00%) 0.7071* C 1 s( 0.00%)p 1.00( 99.96%)d 0.00( 0.04%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.9997 -0.0133
0.0000 0.0096 -0.0170 0.0000 0.0000
( 50.00%) 0.7071* C 2 s( 0.00%)p 1.00( 99.96%)d 0.00( 0.04%)
0.0000 0.0000 0.0000 0.0000 0.0000
0.0000 0.0000 0.0000 0.9997 -0.0133
0.0000 -0.0195 -0.0002 0.0000 0.0000
Orbital 4 is a σ C-H bond formed from an sp2 hybridised carbon and the 1s orbital of hydrogen. At 70% p, the carbon sp2 orbital has slightly more p character than usual. 62% of the electron density is from the carbon atom and only 38% from hydrogen, explained by the greater availability of carbon valence electrons for bonding.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
4. (1.98306) BD ( 1) C 1 - H 7
( 62.04%) 0.7877* C 1 s( 29.57%)p 2.38( 70.39%)d 0.00( 0.04%)
-0.0003 0.5437 0.0126 -0.0010 0.0000
0.0000 0.8389 -0.0146 0.0000 0.0000
0.0000 0.0000 0.0000 -0.0166 -0.0105
( 37.96%) 0.6161* H 7 s( 99.95%)p 0.00( 0.05%)
0.9997 0.0014 0.0000 -0.0228 0.0000
The C-C σ bond, orbital 1, is lowest in energy. The two interacting orbitals are identical in size and energy and therefore have very good overlap. The C-C π bond, orbital 2, is highest in energy. Despite identical size and energy, p-p overlap is poor compared with s-s or s-sp2. The C-H σ bond, orbital 4 is between the two. There is reasonably good overlap between 1s and 2sp2 orbitals.
Principal Delocalizations
NBO Occupancy Energy (geminal,vicinal,remote)
====================================================================================
Molecular unit 1 (C6H6)
1. BD ( 1) C 1 - C 2 1.98098 -0.68189 108(g),110(g),114(v),120(v)
43(v),73(v),109(g),111(g)
42(v),72(v)
2. BD ( 2) C 1 - C 2 1.66514 -0.23791 113(v),118(v),45(v),75(v)
4. BD ( 1) C 1 - H 7 1.98306 -0.51227 110(v),117(v),32(v),72(v)
Molecular Orbitals
The core orbitals form the first six molecular orbitals which are very low in energy. They are not shown on this MO diagram since they are much lower in energy and not involved in mixing.
The σ framework forms the lower energy MOs shown on this diagram. The a1g all-bonding orbital is very low in energy because of the good overlap of C 2s and H 1s orbitals. All of the lower energy occupied MOs involve σ bonding between carbon and hydrogen, with an increasing number of nodal surfaces making the MOs higher in energy.
There are 3 bonding π MOs. The lowest in energy of them forms a bonding π cloud over the whole molecule with the only node in the plane of the ring. This MO takes the form most commonly associated with aromaticity, with its 2 electrons spread across all six carbon atoms. Two π MOs form the degenerate HOMO of benzene, each with two electrons. For one of them two pairs of 3 p orbitals are in phase: there are four bonding p-p interactions and two anti-bonding p-p interactions. Each electron is shared across three of the carbon atoms in the ring. They are therefore delocalised across two C-C bonds not all six. For the other there are two bonding p-p interactions and two weakly anti-bonding p-p interactions. These MOs also contribute to the π cloud of the ring. Each electron resides across a single C-C bond. These are higher in energy than σ bonding MOs because p-p overlap is poorer than s-s or s-p overlap.
The σ framework interleaves with the π framework because they are similar in energy, although on the whole σ MOs are lower in energy than π. The σ and π MOs are distinct because the σ bonding is all in the plane of the ring and the π bonding is orthogonal to it. This means the 6 electrons of the conjugated π system lay above and below the plane of the ring.
A molecule must obey four rules to be classified as aromatic: firstly, the molecule must be cyclic, as is the case with benzene. Secondly, the molecule must be planar. This is verified by the torsion angles of 0° in the optimised molecule. The molecule must be fully conjugated, which it is due to a singly occupied pz orbital on each carbon atom. Finally it must have 4n+2 π electrons, in this case 6π electrons satisfy the rule. The final rule ensures that the bonding π MOs, which can each contain 2 electrons, are filled whilst all of the anti bonding orbitals are empty, conferring the greatest possible stability to the molecule. The delocalisation of π electrons means the system can no longer be seen as a conjugated system of alternating C-C and C=C bonds. This is reflected in the equal bond lengths and strengths determined the NBO analysis. The σ framework already has equal bonding between all the atoms. The aromatic π system pushed the molecule into a planar conformation (cyclohexane is most stable in the chair conformation) adds stability to the molecule through the delocalised rings above and below the plane of the sigma framework. No change in conformation is possible without a very high energy input because it would break the aromaticity of the ring.
Boratabenzene
Optimisation and Frequency
On the optimised .log file of benzene, one carbon atom was replaced by a boron atom and the entire complex assigned a charge of -1. The molecule is isoelectronic with benzene. It was optimised at the B3LYP/6-31G(d,p) level with tight convergence.
Optimisation file: here
| summary data | convergence | Jmol | |||
|---|---|---|---|---|---|
|
Item Value Threshold Converged? Maximum Force 0.000003 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000016 0.000060 YES RMS Displacement 0.000005 0.000040 YES |
|
The frequency calculation was run on the optimised molecule. The low frequencies are within the acceptable range and the vibrational frequencies are all positive, indicating the optimisation to a minimum was successful.
Frequency file: here
| summary data | low modes |
|---|---|
|
Low frequencies --- -7.1296 0.0007 0.0007 0.0008 3.5040 4.6998 Low frequencies --- 371.3002 404.4179 565.0778 |
The molecule has C2v symmetry without being constrained prior to optimisation.
Boratabenzene also has 30 vibrational modes but many more are IR active than in benzene. This is because by removing many symmetry elements from the molecule, more vibrational modes change the overall dipole moment and are therefore IR active. Only 3 of the 30 modes are IR inactive (intensity of zero) but several more result in such small changes in the overall dipole that the intensity is too low to be easily observed on the IR spectrum. Modes that were degenerate in benzene are also no longer degenerate in the less symmetrical boratabenzene molecule.
NBO Analysis
An energy calculation was run on the optimised molecule.
NBO file here
| Details | Charge Distribution | Charge Values |
|---|---|---|
|

|

|
The charge distribution has changed greatly with the replacement of a carbon by a boron atom. The H attached to B now carries a slight negative charge unlike the positively charged Hs attached to C. The C atoms directly bonded to B are also much more negatively charged than the meta carbons, and the para carbon in between the two. With a Pauling electronegativity of 2.04, boron is the most electropositive atom in the molecule and replaces the more electronegative carbon (Pauling electronegativity of 2.55). This disrupts the pattern of the inner ring of negatively charged carbons and outer ring of positively charged hydrogens.
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
C 1 -0.58805 1.99901 4.57725 0.01178 6.58805
C 2 -0.25033 1.99910 4.23710 0.01413 6.25033
C 3 -0.34002 1.99907 4.32711 0.01384 6.34002
C 4 -0.25033 1.99910 4.23710 0.01413 6.25033
C 5 -0.58805 1.99901 4.57725 0.01178 6.58805
H 6 -0.09650 0.00000 1.09596 0.00054 1.09650
H 7 0.18385 0.00000 0.81397 0.00218 0.81615
H 8 0.17899 0.00000 0.81838 0.00263 0.82101
H 9 0.18574 0.00000 0.81227 0.00199 0.81426
H 10 0.17899 0.00000 0.81838 0.00263 0.82101
H 11 0.18385 0.00000 0.81397 0.00218 0.81615
B 12 0.20186 1.99906 2.78748 0.01160 4.79814
=======================================================================
* Total * -1.00000 11.99436 29.91623 0.08941 42.00000
The C-C σ bonding orbitals in boratabenzene differ slightly from those in benzene because the carbon atoms are no longer identical. One of the sp2 orbitals has more p character than the other and contributes less of the electron density. The C-C bonds are no longer all the same: orbital 1 shown below is between the ortho and meta carbons, orbital 5 is between the meta and para carbons. The main difference between the two bonds is the hybridisations of the interacting orbitals. In orbital 1 there is more p character to the orbital of the carbon bonded to boron, whereas in orbital 5 the two carbons have roughly the same hybridisation.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.98271) BD ( 1) C 1 - C 2
( 49.23%) 0.7017* C 1 s( 32.51%)p 2.08( 67.45%)d 0.00( 0.05%)
0.0000 0.5698 -0.0200 0.0010 0.0000
0.0000 -0.0028 0.0270 0.8201 0.0353
0.0000 0.0000 0.0006 -0.0020 0.0212
( 50.77%) 0.7125* C 2 s( 37.60%)p 1.66( 62.37%)d 0.00( 0.03%)
-0.0001 0.6131 -0.0079 0.0007 0.0000
0.0000 0.0575 0.0311 -0.7869 -0.0164
0.0000 0.0000 -0.0020 -0.0010 0.0179
5. (1.97969) BD ( 1) C 2 - C 3
( 49.96%) 0.7068* C 2 s( 35.53%)p 1.81( 64.43%)d 0.00( 0.04%)
-0.0001 0.5960 -0.0075 0.0006 0.0000
0.0000 -0.6872 -0.0034 0.4135 0.0325
0.0000 0.0000 -0.0146 -0.0133 -0.0016
( 50.04%) 0.7074* C 3 s( 35.87%)p 1.79( 64.10%)d 0.00( 0.04%)
-0.0001 0.5989 -0.0072 0.0010 0.0000
0.0000 0.7062 0.0327 -0.3754 0.0141
0.0000 0.0000 -0.0137 -0.0131 -0.0014
The π bonding is also no longer between identical carbons. The atom that contributes less of the σ bonding electron density donates more of the π bonding electrons. The occupancy of the C-C π bonding orbital is greater in boratazine than in benzene but there are only two. One C-B π bond would be expected if the delocalision is across all six atoms of the ring but none appears in the NBO analysis.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
2. (1.76874) BD ( 2) C 1 - C 2
( 51.88%) 0.7202* C 1 s( 0.00%)p 1.00( 99.97%)d 0.00( 0.03%)
0.0000 0.0000 0.0000 0.0000 0.9998
-0.0054 0.0000 0.0000 0.0000 0.0000
-0.0016 0.0185 0.0000 0.0000 0.0000
( 48.12%) 0.6937* C 2 s( 0.00%)p 1.00( 99.97%)d 0.00( 0.03%)
0.0000 0.0000 0.0000 0.0000 0.9996
-0.0213 0.0000 0.0000 0.0000 0.0000
-0.0031 -0.0171 0.0000 0.0000 0.0000
Two-thirds of the electron density on the C-B σ bond is in the carbon orbital, which has very high s character. This is because boron is more electropositive. The boron orbital has nearly perfect sp2 hybridisation.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
4. (1.96998) BD ( 1) C 1 - B 12
( 66.70%) 0.8167* C 1 s( 42.00%)p 1.38( 57.99%)d 0.00( 0.01%)
0.0000 -0.6479 -0.0159 -0.0012 0.0000
0.0000 0.6117 -0.0293 0.4525 0.0090
0.0000 0.0000 -0.0059 0.0070 0.0007
( 33.30%) 0.5771* B 12 s( 33.40%)p 1.99( 66.53%)d 0.00( 0.08%)
0.0000 -0.5779 0.0059 -0.0049 0.0000
0.0000 -0.7056 -0.0393 -0.4071 0.0096
0.0000 0.0000 -0.0230 0.0156 0.0005
Compared to the C-H bond in benzene, carbon contributes less electron density to the bond and its hybridised orbital has greater p character. In C-H bonds, carbon donates nearly 60% of the electron density of the bonding orbital, whereas in B-H bonds boron donates only 45%. In both cases it is the more electronegative atom's orbitals donating most of the electron density. The bond would also be expected to be more polarised towards the more electronegative atom.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
3. (1.98422) BD ( 1) C 1 - H 7
( 59.41%) 0.7708* C 1 s( 25.40%)p 2.93( 74.55%)d 0.00( 0.05%)
0.0003 -0.5040 0.0051 0.0025 0.0000
0.0000 -0.7905 0.0002 0.3470 0.0088
0.0000 0.0000 0.0111 0.0178 0.0070
( 40.59%) 0.6371* H 7 s( 99.95%)p 0.00( 0.05%)
-0.9998 -0.0005 0.0000 0.0191 -0.0100
14. (1.98608) BD ( 1) H 6 - B 12
( 55.09%) 0.7422* H 6 s( 99.97%)p 0.00( 0.03%)
0.9998 0.0001 0.0000 0.0000 0.0180
( 44.91%) 0.6702* B 12 s( 33.17%)p 2.01( 66.78%)d 0.00( 0.06%)
-0.0005 0.5758 0.0069 -0.0060 0.0000
0.0000 0.0000 0.0000 -0.8172 0.0016
0.0000 0.0000 0.0000 0.0016 0.0237
The C-C σ bond is still the lowest energy bonding orbital. The C-B σ bond is slightly higher in energy because the interacting orbitals are further apart in energy and do not have as good spatial overlap. As in benzene, the C-H σ bond is slightly higher in energy than the other σ bonds and the C-C π bond is much higher in energy than all the others.
Principal Delocalizations
NBO Occupancy Energy (geminal,vicinal,remote)
====================================================================================
Molecular unit 1 (C5H6B)
1. BD ( 1) C 1 - C 2 1.98271 -0.46502 110(g),111(g),114(v),112(g)
44(v),120(v),109(g),98(v)
43(v)
2. BD ( 2) C 1 - C 2 1.76874 -0.02908 21(v),22(v),45(v),100(v)
108(g)
3. BD ( 1) C 1 - H 7 1.98422 -0.28859 111(v),110(g),33(v),119(v)
97(v),107(g)
4. BD ( 1) C 1 - B 12 1.96998 -0.31755 107(g),112(v),118(v),109(g)
34(v),33(v),77(v),64(v)
119(g)
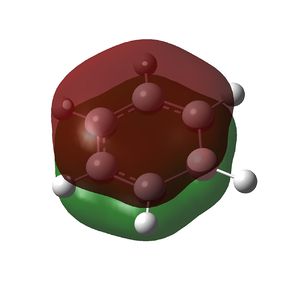
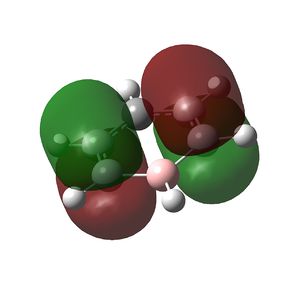
Despite the length of the C-B bond and lack of a C-B π bonding orbital in the NBO analysis, boratabenzene's aromaticity is verified by MO analysis. The molecule also obeys the rules of Huckel aromaticity: it is a planar conjugated ring system with 6π electrons. There are 3 occupied π bonding MOs shown below.
|
|
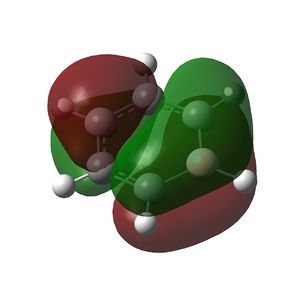
|
Population file here
Pyridinium
Optimisation and Frequency
On the optimised .log file of benzene, one carbon atom was replaced by a nitrogen atom and the entire complex assigned a charge of +1 so that it too is isoelectronic with benzene and boratabenzene. The molecule was optimised at the B3LYP/6-31G(d,p) level with tight convergence.
Optimisation file: here
| summary data | convergence | Jmol | |||
|---|---|---|---|---|---|
|
Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000005 0.000060 YES RMS Displacement 0.000002 0.000040 YES |
|
The molecule also has C2v symmetry.
The frequency calculation was run on the optimised molecule. The low frequencies are within the acceptable range and the vibrational frequencies are all positive, indicating the optimisation to a minimum was successful.
Frequency file: here
| summary data | low modes |
|---|---|
|
Low frequencies --- -9.3865 -3.0390 -0.0011 -0.0006 -0.0005 1.1195 Low frequencies --- 391.9013 404.3417 620.2000 |
Similarly to boratabenzene, there are 30 vibrational modes of which 27 are IR active and 3 are IR inactive. The molecule does not have many symmetry elements so there are few degenerate or IR inactive modes, resulting in many more IR peaks than in benzene. Many modes do not cause large charges in dipole moment though, so the intensities of many peaks are low.
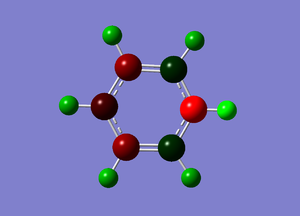
NBO Analysis
NBO file here
| Details | Charge Distribution | Charge Values |
|---|---|---|
|
|
|
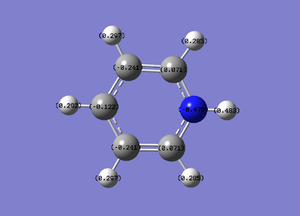
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
C 1 0.07102 1.99918 3.91065 0.01916 5.92898
C 2 -0.24107 1.99912 4.22863 0.01331 6.24107
C 3 -0.12238 1.99913 4.10938 0.01386 6.12238
C 4 -0.24107 1.99912 4.22863 0.01331 6.24107
C 5 0.07102 1.99918 3.91065 0.01916 5.92898
H 6 0.48278 0.00000 0.51476 0.00246 0.51722
H 7 0.28493 0.00000 0.71397 0.00110 0.71507
H 8 0.29720 0.00000 0.70178 0.00103 0.70280
H 9 0.29169 0.00000 0.70719 0.00113 0.70831
H 10 0.29720 0.00000 0.70178 0.00103 0.70280
H 11 0.28493 0.00000 0.71397 0.00110 0.71507
N 12 -0.47623 1.99937 5.46756 0.00929 7.47623
=======================================================================
* Total * 1.00000 11.99510 29.90895 0.09595 42.00000
As in boratabenzene, the C-C bonds are no longer identical. In each there are slight differences in relative contributions and in hybridisation as can be seen in orbitals 1 and 5 below. The difference between the hybridisations of the two carbons is greater in the bond between ortho and meta carbons (orbital 1) than between meta and para carbons (orbital 5).
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.98297) BD ( 1) C 1 - C 2
( 50.42%) 0.7100* C 1 s( 38.50%)p 1.60( 61.46%)d 0.00( 0.04%)
0.0001 -0.6204 0.0024 -0.0030 0.0000
0.0000 -0.0141 -0.0331 0.7831 0.0046
0.0000 0.0000 -0.0053 -0.0002 -0.0193
( 49.58%) 0.7042* C 2 s( 33.48%)p 1.99( 66.48%)d 0.00( 0.05%)
0.0000 -0.5785 0.0119 0.0002 0.0000
0.0000 0.0007 -0.0320 -0.8145 -0.0194
0.0000 0.0000 0.0047 0.0014 -0.0215
5. (1.98249) BD ( 1) C 2 - C 3
( 50.26%) 0.7089* C 2 s( 34.72%)p 1.88( 65.23%)d 0.00( 0.04%)
0.0000 0.5892 -0.0066 0.0009 0.0000
0.0000 -0.6898 0.0068 -0.4184 -0.0371
0.0000 0.0000 0.0122 -0.0159 -0.0045
( 49.74%) 0.7053* C 3 s( 34.45%)p 1.90( 65.51%)d 0.00( 0.04%)
0.0000 0.5869 -0.0086 0.0005 0.0000
0.0000 0.7063 0.0290 0.3934 -0.0234
0.0000 0.0000 0.0169 -0.0127 0.0004
Unlike in boratabenzene, there is a π as well as a σ bond between nitrogen and carbon. Both the bonds have greater electron density from the more electronegative nitrogen atom. The occupancy of the C-N π bond is greater than that of the C-C in benzene.
3. (1.98862) BD ( 1) C 1 - N 12
( 36.68%) 0.6057* C 1 s( 28.13%)p 2.55( 71.74%)d 0.00( 0.13%)
-0.0001 0.5293 -0.0334 -0.0013 0.0000
0.0000 -0.7417 -0.0277 0.4042 0.0563
0.0000 0.0000 -0.0252 -0.0247 -0.0070
( 63.32%) 0.7957* N 12 s( 36.56%)p 1.73( 63.41%)d 0.00( 0.03%)
-0.0001 0.6046 -0.0037 0.0006 0.0000
0.0000 0.7069 0.0132 -0.3659 0.0187
0.0000 0.0000 -0.0107 -0.0129 0.0007
4. (1.82446) BD ( 2) C 1 - N 12
( 28.54%) 0.5343* C 1 s( 0.00%)p 1.00( 99.83%)d 0.00( 0.17%)
0.0000 0.0000 0.0000 0.0000 0.9991
0.0132 0.0000 0.0000 0.0000 0.0000
-0.0394 0.0102 0.0000 0.0000 0.0000
( 71.46%) 0.8453* N 12 s( 0.00%)p 1.00( 99.98%)d 0.00( 0.02%)
0.0000 0.0000 0.0000 0.0000 0.9999
0.0036 0.0000 0.0000 0.0000 0.0000
0.0077 -0.0128 0.0000 0.0000 0.0000
The C-C π bonds have lower electron occupancy than both the C-N π bond and the C-C π bond in benzene. This can be explained by the more electronegative nitrogen atom drawing the delocalised electrons towards it.
6. (1.54875) BD ( 2) C 2 - C 3
( 54.28%) 0.7367* C 2 s( 0.00%)p 1.00( 99.94%)d 0.00( 0.06%)
0.0000 0.0000 0.0000 0.0000 0.9997
-0.0080 0.0000 0.0000 0.0000 0.0000
-0.0228 0.0086 0.0000 0.0000 0.0000
( 45.72%) 0.6762* C 3 s( 0.00%)p 1.00( 99.93%)d 0.00( 0.07%)
0.0000 0.0000 0.0000 0.0000 0.9997
-0.0036 0.0000 0.0000 0.0000 0.0000
0.0101 0.0241 0.0000 0.0000 0.0000
The N-H bond is more polarised towards N than the C-H bond is towards C because of the greater difference in electronegativities. The N orbital also has more p character than the C orbital.
13. (1.98154) BD ( 1) C 5 - H 11
( 64.26%) 0.8016* C 5 s( 33.44%)p 1.99( 66.52%)d 0.00( 0.04%)
0.0004 -0.5780 -0.0180 0.0017 0.0000
0.0000 0.6665 -0.0183 -0.4694 0.0193
0.0000 0.0000 0.0164 0.0089 -0.0030
( 35.74%) 0.5978* H 11 s( 99.94%)p 0.00( 0.06%)
-0.9997 -0.0018 0.0000 -0.0209 0.0128
15. (1.98630) BD ( 1) H 6 - N 12
( 25.41%) 0.5041* H 6 s( 99.88%)p 0.00( 0.12%)
0.9994 -0.0064 0.0000 0.0000 -0.0342
( 74.59%) 0.8637* N 12 s( 26.82%)p 2.73( 73.15%)d 0.00( 0.02%)
-0.0002 0.5178 0.0066 -0.0013 0.0000
0.0000 0.0000 0.0000 0.8553 -0.0091
0.0000 0.0000 0.0000 -0.0034 0.0153
The lowest energy bonding orbital is the C-N σ bond. Carbon and nitrogen have similar sizes so orbital overlap would be good, and the lower electronegativity of nitrogen would lower the bond energy. The C-C bond adjacent to nitrogen has slightly lower energy than the bond further away, both of which are lower energy than the bonds in benzene. The N-H bond is lower in energy than the C-H bond for the same reasons and C-N is lower in energy than C-C. The C-N π bond is also lower in energy than the C-C π bond.
Principal Delocalizations
NBO Occupancy Energy (geminal,vicinal,remote)
====================================================================================
Molecular unit 1 (C5H6N)
1. BD ( 1) C 1 - C 2 1.98297 -0.92652 120(v),114(v),110(g),43(v)
107(g),97(v),112(g),42(v)
108(g),96(v)
2. BD ( 1) C 1 - H 7 1.98154 -0.75116 119(v),110(v),32(v),106(g)
96(v)
3. BD ( 1) C 1 - N 12 1.98862 -1.06555 119(g),62(v),112(v),33(v)
118(v),63(v),106(g),120(g)
4. BD ( 2) C 1 - N 12 1.82446 -0.56810 116(v),111(v),64(v),36(v)
5. BD ( 1) C 2 - C 3 1.98249 -0.90379 107(v),117(v),106(g),24(v)
113(g),112(g),53(v),52(v)
114(g)
6. BD ( 2) C 2 - C 3 1.54875 -0.44892 109(v),116(v),26(v),56(v)
15. BD ( 1) H 6 - N 12 1.98630 -0.89233 106(v),115(v),22(v),62(v)
Multiple bonding in the ring is observed in the NBO analysis and aromaticity is confirmed by the presence of delocalised π orbitals. Again, the ring is planar and has conjugated π bonding of 4n + 2 = 6 π electrons so it satisfies Huckel's rules for aromaticity. The π-bonding molecular orbitals are shown below. The π cloud is larger around nitrogen due to the higher electron density on the more electronegative atom.
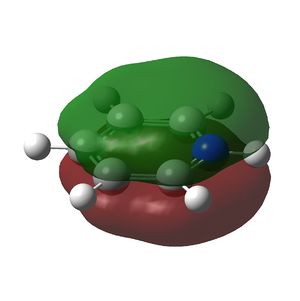
|
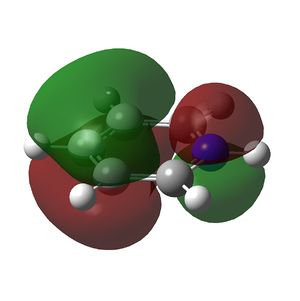
|
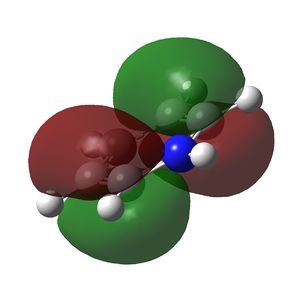
|
MO file here
Borazine
Borazine is a 6-membered ring formed of alternating N-H and B-H units. Boron has one electron less than carbon, and nitrogen one more, so the molecule is isoelectronic with benzene.
Optimisation and Frequency
Optimisation file: here
| summary data | convergence | Jmol | |||
|---|---|---|---|---|---|
|
Item Value Threshold Converged? Maximum Force 0.000001 0.000015 YES RMS Force 0.000000 0.000010 YES Maximum Displacement 0.000005 0.000060 YES RMS Displacement 0.000002 0.000040 YES |
|
The molecule has D3h symmetry.
The frequency calculation was run on the optimised molecule. The low frequencies are within the acceptable range and the vibrational frequencies are all positive, indicating the optimisation to a minimum was successful.
Frequency file: here
| summary data | low modes |
|---|---|
|
Low frequencies --- -4.0171 -3.0397 -0.0008 0.0002 0.0005 4.3402 Low frequencies --- 289.7186 289.7942 404.5430 |
Borazine also has 30 vibrational modes. It has 3-fold symmetry so fewer of these modes are IR inactive or degenerate than in benzene, but more than in boratabenzene or pyridinium.
NBO Analysis
NBO file here
| Details | Charge Distribution | Charge Values |
|---|---|---|
|
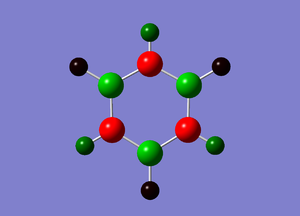
|

|
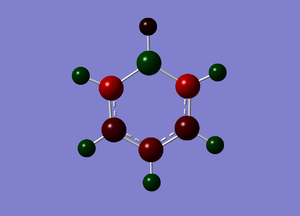
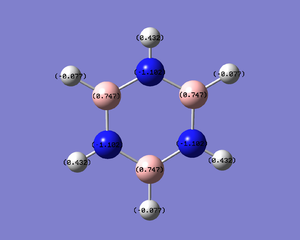
In the charge distribution above and the natural population summary below, it can be seen than all the N-H units are identical and all the B-H units are identical, confirming the 3-fold symmetry. The hydrogen atoms attached to the more electronegative nitrogens are positively charged, while those bonded to electropositive boron are negatively charged. The charges are distributed over a much larger range in borazine than the other molecules studied because of the large difference in electronegativites between nitrogen and boron.
Natural Population
Natural -----------------------------------------------
Atom No Charge Core Valence Rydberg Total
-----------------------------------------------------------------------
H 1 0.43200 0.00000 0.56571 0.00228 0.56800
H 2 -0.07654 0.00000 1.07584 0.00069 1.07654
H 3 0.43200 0.00000 0.56571 0.00228 0.56800
H 4 -0.07654 0.00000 1.07584 0.00069 1.07654
H 5 0.43200 0.00000 0.56571 0.00228 0.56800
H 6 -0.07654 0.00000 1.07584 0.00069 1.07654
N 7 -1.10240 1.99943 6.09820 0.00478 8.10240
N 8 -1.10240 1.99943 6.09820 0.00478 8.10240
N 9 -1.10240 1.99943 6.09820 0.00478 8.10240
B 10 0.74694 1.99917 2.23868 0.01521 4.25306
B 11 0.74694 1.99917 2.23868 0.01521 4.25306
B 12 0.74693 1.99917 2.23869 0.01521 4.25307
=======================================================================
* Total * 0.00000 11.99579 29.93530 0.06891 42.00000
The electrons are localised mainly on nitrogen in the N-H bond and mainly on hydrogen in the B-H bond. Boths bonds are polarised towards the more electronegative atom.
(Occupancy) Bond orbital/ Coefficients/ Hybrids
---------------------------------------------------------------------------------
1. (1.98494) BD ( 1) H 1 - N 7
( 28.08%) 0.5299* H 1 s( 99.91%)p 0.00( 0.09%)
0.9996 -0.0010 0.0000 0.0000 -0.0295
( 71.92%) 0.8481* N 7 s( 22.82%)p 3.38( 77.15%)d 0.00( 0.03%)
-0.0002 0.4776 -0.0114 0.0006 0.0000
0.0000 0.0000 0.0000 0.8782 0.0130
0.0000 0.0000 0.0000 -0.0042 0.0165
2. (1.98670) BD ( 1) H 2 - B 11
( 54.03%) 0.7351* H 2 s( 99.96%)p 0.00( 0.04%)
0.9998 0.0002 0.0000 -0.0166 -0.0096
( 45.97%) 0.6780* B 11 s( 37.47%)p 1.67( 62.47%)d 0.00( 0.07%)
-0.0006 0.6120 0.0129 -0.0016 0.0000
0.0000 0.6841 -0.0233 0.3950 -0.0135
0.0000 0.0000 0.0204 -0.0144 -0.0053
Similarly, the B-N bonds are all polarised towards nitrogen. This effect is more pronounced in the π bond (orbital 9) than in the σ bond (orbital 7). The presence of 3 B-N π bonding orbitals and identical N-H and B-H units suggests delocalised π bonding and aromaticity are also present in borazine. The π bonds in benzene are formed from overlap of carbon pz orbitals each with one electron. In borazine they are formed from delocalisation of electrons from the filled pz orbitals (lone pairs) on nitrogen into the empty pz orbitals on boron. It is therefore unsurprising that more electron density remains on nitrogen than on boron.
7. (1.98437) BD ( 1) N 7 - B 10
( 76.47%) 0.8745* N 7 s( 38.55%)p 1.59( 61.44%)d 0.00( 0.01%)
0.0000 -0.6209 -0.0043 0.0001 0.0000
0.0000 0.7071 -0.0001 0.3379 -0.0159
0.0000 0.0000 -0.0057 0.0096 -0.0005
( 23.53%) 0.4851* B 10 s( 31.25%)p 2.19( 68.50%)d 0.01( 0.25%)
0.0003 -0.5588 0.0174 -0.0032 0.0000
0.0000 -0.7259 -0.0213 -0.3933 -0.0538
0.0000 0.0000 -0.0360 0.0315 0.0134
9. (1.82089) BD ( 2) N 7 - B 11
( 88.21%) 0.9392* N 7 s( 0.00%)p 1.00(100.00%)d 0.00( 0.00%)
0.0000 0.0000 0.0000 0.0000 1.0000
-0.0003 0.0000 0.0000 0.0000 0.0000
0.0005 -0.0046 0.0000 0.0000 0.0000
( 11.79%) 0.3433* B 11 s( 0.00%)p 1.00( 99.62%)d 0.00( 0.38%)
0.0000 0.0000 0.0000 0.0000 0.9976
-0.0315 0.0000 0.0000 0.0000 0.0000
-0.0573 0.0220 0.0000 0.0000 0.0000
The same trends in bond energies are seen in borazine as in the other molecules studied. The N-B sigma bond is lowest in energy, followed by the N-H then the B-H. The pi bond is highest in energy.
Principal Delocalizations
NBO Occupancy Energy (geminal,vicinal,remote)
====================================================================================
Molecular unit 1 (H6B3N3)
1. BD ( 1) H 1 - N 7 1.98494 -0.61485 115(v),118(v),112(g),113(g)
76(v),86(v)
2. BD ( 1) H 2 - B 11 1.98670 -0.40387 112(v),116(v),46(v),56(v)
8. BD ( 1) N 7 - B 11 1.98437 -0.68877 112(g),108(v),106(g),111(v)
77(v),118(v)
9. BD ( 2) N 7 - B 11 1.82089 -0.27142 119(v),82(v),78(v),23(v)
Borazine is a planar ring with 6 π electrons in a conjugated system and also displays aromaticity as can be seen in the molecular orbitals below.
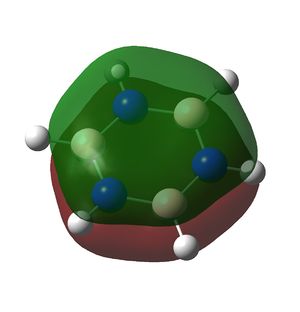
|
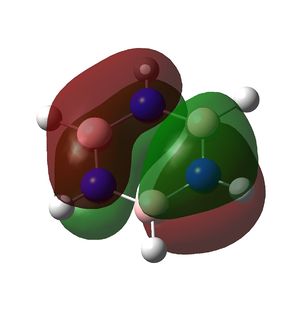
|
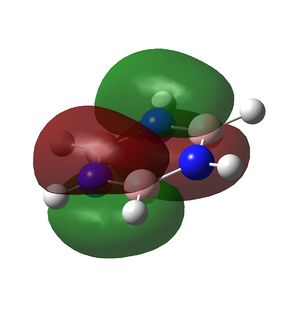
|
MO file here
Comparison of NBOs
Charge Distribution
Benzene has an even distribution of charge across all the carbon atoms and across all the hydrogen atoms. Likewise in borazine, all the nitrogen atoms have the same charge, as do all the boron atoms. All the hydrogens bound to nitrogen have the same charge, and all those bound to boron. Boratazine and pyridinium have much lower symmetry and this is reflected in their charge distribution. The introduction of a heteroatom on the ring changes the charge density of the ortho, meta and para carbons and hydrogens.
In boratazine, the H bound to B now bears a small negative charge. The carbon atoms directly bound to boron have the greatest increase in negative charge, and the para carbons the next greatest. The charge on the meta carbons increases by very little. The positive charge on the hydrogens bound to carbons have all decreased. The decrease is greater for the meta hydrogens.
In pyridinium, the H bound to N has a more positive charge. The hydrogens bound to carbon are slightly more positvely charged than those in benzene. The carbon atoms directly bound to nitrogen are now slightly positively charged and the negative charge on the para carbon has been approximately halved. Again, the introduction of a heteroatom has little effect on the charge of the meta carbons.
| Benzene | Boratabenzene | Pyridinium | Borazine |

|
|

|

|

|

|

|
|
The table above shows all the molecules with the charge distribution coloured across the same range -1.102 to 1.102. The difference in charges is much greater in borazine, where there is a large difference in electronegativity between boron and nitrogen, than in any of the other rings where the range of electronegativities is much smaller.
Bonding
Boratabenzene:
The introduction of a boron atom lengthens the bonds in the ring by different amounts and in doing so distorts the intrannular angles. The C-C bonding still appears to be delocalised across the 5 carbon atoms with a bond length of 1.40 - 1.41 Å. The C-B bonds are longer at 1.51 Å but this is explained by the larger covalent radius of boron than carbon. The torsion angles are still zero, confirming that the ring remains planar. The intrannular angle is compressed to 115.1° at boron so two other angles are extended to 122.2° to compensate. As expected, the C-B bond is weaker than the C-C bonds due to poorer overlap between carbon and boron atomic orbitals and due to the higher energy atomic orbitals of electropositive boron. Both the σ and π C-C bonds of this molecule are also weaker than those in benzene. The carbon atoms no longer have degenerate energies so the stabilisation energy from interaction would be lower, leading to weaker bonds.
Pyridinium:
The substitution of one carbon by nitrogen has the opposite effect. The C-N-C bond angle is wider at 123.3° and the N-C-C and C-C-C angles slightly smaller at 119-120° to accomodate the change. The C-N bonds are shorter than C-C bonds at 1.35 Å. This can be explained both by the smaller covalent radius of nitrogen and by the difference in electronegativity between carbon and nitrogen, making the bond stronger and more ionic. The C-C bonds are relatively unaffected, at 1.38 - 1.39 Å. The molecule is planar. Nitrogen is electronegative so it has lower-lying atomic orbitals. As a result, all the bonding orbitals in pyridinium lie lower in energy than those in benzene.
Borazine:
Its torsion angles are all 0°, indicating the molecule is planar. The B-N-B angles are all 122.9° and the N-B-N angles 117.1° so the shape is slightly distorted from the perfect hexagon of benzene. The bond lengths are all slightly longer at 1.43 Å, but between B-N single bonds (1.51 Å) and B-N double bonds (1.31 Å) indicating delocalisation. The delocalised electrons originate from the pz lone pair on each nitrogen. The nitrogen and boron bonds are further apart in energy and have worse spatial overlap than any of the C-C, N-C or B-C bonds seen above so the bonds would be expected to be longer and weaker. The energies of the σ and π bonding orbitals between N and B are similar to those of the C-C bonds in benzene. N-H bonds are lower in energy and shorter than B-H bonds.
Comparison of Molecular Orbitals
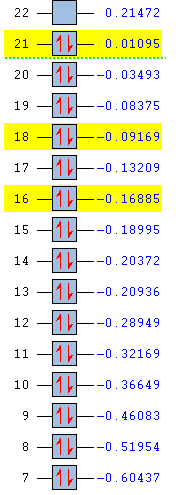
Three molecular orbitals were compared across the four molecules studied. As seen in the figure below, the MOs are all formed from linear combination of the same set of atomic orbitals. However, changing one or more substituent in the ring affects the energies of the atomic orbitals and therefore their relative contributions to the molecular orbital. This effects is minimal in the π bonding MO shown below where only small changes in the size and shape of the MO are seen. The effect is more pronounced in the MO in the middle row, where p and s orbitals interact: there are significant changes in the size of the lobes but not in their shape. The effect is greatest in the bottom row where different orbitals in phase combine to form lobes of different shapes and sizes. There are still three nodal surfaces in each MO but they have significantly different shapes from one molecule to the next. In benzene there is a flat central nodal surface and two u-shaped ones on either side. In the other three molecules, the nodal surfaces are all u-shaped and become progressively larger from one end to the other.
Modifying the atoms in the ring also changes the symmetry of the molecular orbitals. The π orbital studied here has e1g symmetry in benzene, which is reduced to a2 in borazine and b2 in pyridinium and boratabenzene. MO 19 of benzene (middle row) has e2g symmetry is benzene but only a1 in borazine, pyridinium and benzene. MO 16 in benzene, e1u likewise only has a1 symmetry in the other three molecules. This loss of symmetry affects all the molecular orbitals of the molecule not just the three studied here.
| Benzene | Pyridinium | Boratabenzene | Borazine |
|---|---|---|---|
|
|
|

|
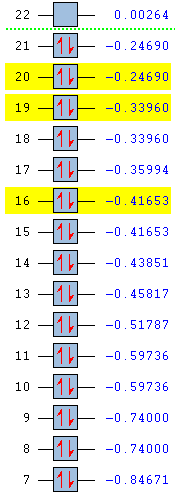
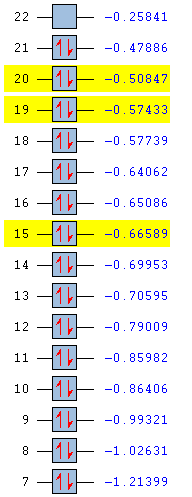
The energies are shown in the table above, with the MOs of interest highlighted in yellow. The energy values as well as their ordering differs between the molecules. The three orbitals studied are degenerate with another MO in benzene and borazine, but the reduction in symmetry in pyridinium and boratabenzene has removed all degeneracy.
Pyridinium has lower energy occupied MOs than benzene. Substitution of one carbon atom by nitrogen appears to have stabilised the molecule overall. This is also reflected in the stronger bonding in pyridinium. In removing the degeneracy, all three MOs have become lower in energy than their previously degenerate pairs. Nitrogen is more electronegative than carbon so its atomic orbitals are lower in energy. Its orbitals are included in the molecular orbitals shown above but not in their previously degenerate partners, hence the relative stabilisation.
All of the occupied MOs in boratabenzene are much higher in energy than those in benzene and the HOMO now has positive energy, suggesting the molecule might be less stable than benzene. This can be seen on the MO pictures above, where the in-phase areas are smaller. These higher energy MOs are expected due to weaker bonding in boratabenzene compared with benzene. Two of the three MOs (top and bottom) are now higher in energy than MOs with which they were previously degenerate. This could be due to the higher energy atomic orbitals on boron.
The degeneracy is maintained in borazine which still has three-fold symmetry. The orbital energies are also very similar to benzene, presumably because the low energy orbitals of electronegative nitrogen and higher energy orbitals of electropositive boron counteract each other. The top and middle MOs maintain their ordering with respect to benzene, but the lowest of the three orbitals studied has dropped below two other MOs. The nodal surfaces take on a completely different form than in benzene and the lobes incorporate different atoms, which must have a stabilising effect relative to the MOs similar in energy. Benzene has 6 pairs of non-core degenerate occupied molecular orbitals, boratabenzene and pyridinium have none and borazine has 5. This is due to benzene having the highest degree of symmetry, borazine having a lower degree and the other two molecules having very little symmetry.
The HOMO-LUMO gap is largest in benzene and smallest in boratabenzene. This is a good indicator of the stability of the molecule and indeed benzene is extremely stable while boratabenzene is highly reactive.
The main effect these substitutions have on the full MO diagram are the ordering, energy and degeneracy of all the MOs. The symmetry labels of many of the orbitals would change as the symmetry of the molecule is reduced. Some aspects of the MO diagrams would remain unchanged, such as the presence of 6 core orbitals very low in energy and of 3 valence π orbitals that form the aromatic π system. The overall occupancy would not change because the molecules are all isoelectronic, but the HOMO and LUMO orbitals differ across the molecules.