Mod:ts tutorial temp
Transition States Tutorial
Locating transition states with Gaussian
Transition States
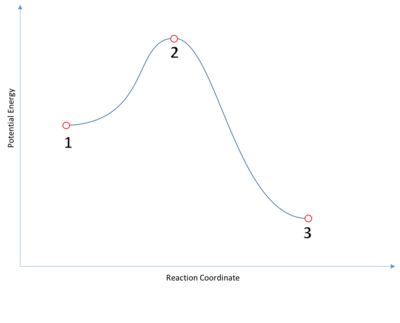
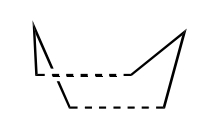
A transition state is the highest energy point along a reaction coordinate. It is therefore a stationary point (i.e. a gradient of zero) with a negative second derivative along the reaction coordinate. Locating transition states is an important step in confirming the mechanism of a reaction - for example, is a particular reaction stepwise or concerted? The following is a familiar depiction of a reaction coordinate, where a set of reactants (1) and products (3) are linked by a transition state (2).
Beyond 1D - The Potential Energy Surface
In reality, a chemical system undergoing a reaction will explore more than the reaction coordinate - it can be displaced away from its equilibrium position in any degree of freedom. The potential energy can be plotted against any one or a combination of these degrees of freedom or coordinates. Setting the system in equilibrium about every degree of freedom (minimising) and varying 1 coordinate yields an Energy Profile (above). Below, we see the result of varying 2 coordinates, commonly known as a Potential Energy Surface.
The above example shows the dimerisation of cyclopentadiene. In Coordinate 1 (bottom to top), the bonding atoms are brought closer together and sp3 hybridised. In Coordinate 2 (left to right), the cyclopentadiene molecules are rotated about the reaction centre (twisted). This PES shows some twisting is required to prevent the atoms getting too close to the highlighted methylene.
These coordinates are in fact the first two normal modes of the system. Recalling the number of normal modes of vibration = 3N - 6, this system with 22 atoms has 60 normal modes. You can have a look at some of the other vibrations in the example above by right clicking and selecting a model. Models 1-20 are steps of an optimisation calculation, and models 21-80 are the 60 normal modes. You should notice that the first normal mode has a 'negative' frequency. This negative is meant to depict an imaginary number, the result of calculating the frequency of a harmonic oscillator with a negative force constant (square of a negative).
At every transition state there must be only one imaginary frequency as all other coordinates are minimised. There are methods to resolve calculations that yield more negative frequencies than expected.
Check the Troubleshooting page if you are stuck and a demonstrator isn't available.
Locating Transition States with Gaussian
Make sure you are familiar with the table of controls in the Basic GaussView Tutorial before beginning this tutorial
This section makes use of the semi-empirical method PM6 to generate approximate structures, followed by the DFT method B3LYP. The reason to do this is speed - each step of a DFT calculation typically takes much longer and uses more computational resources than PM6, but yields better results.
Method 1
Advantages: Fastest method Disadvantages: Very unreliable. Requires knowledge of the TS Going straight for a TS optimisation is not recommended unless you are very sure that you are close to the TS. This can only really be used for very small systems. Often the calculation will fail, the wrong TS will be found or there will be multiple imaginary frequencies (shown as a negative number in GaussView and Gaussian). A converged structure with multiple imaginary frequencies is indicative of a higher order saddle point.
Step 2: Set up the calculation. In the Job Type tab, choose Opt+Freq. Optimise to a TS (Berny), set 'Calculate force constants' to 'once'*. In the Method window, choose 'Semi-empirical' (second dropdown box) and choose PM6 as the method. *Force constants are required for TS calculations. The algorithm must have the local curvature as an input to 'know' which direction the reaction path is. Step 3: Press 'Submit'. Note that using the Windows computers you can run into serious errors by running multiple jobs simultaneously. If the job succeeds, open the log file. If it doesn't, go to the Troubleshooting page. Hopefully it should look like the TS you were expecting. Right click on the window and select 'Results' then 'Vibrations'. Here you can check the number of vibrations and visualise them. If there is more than one negative frequency, go to the Troubleshooting section. If there is one, check that it is correct by choosing it and pressing 'Start Animation'. The vibration should correspond to the reaction coordinate (i.e. it should look like it's going between the reactants and products). Step 4: If the results are fine, you can now reoptimise with a more accurate method if necessary. Copy the structure to a new window (Shortcut: ctrl + (C, N, V) ). Using B3LYP/6-31G(d) as an example, repeat steps 2 and 3, but this time choose B3LYP as the method (Semi-empirical must be changed to DFT). For the basis set choose 6-31 and (d) for the polarisation function. The keywords line should now contain "b3lyp/6-31g(d)". With the new method and basis set you can optimise to a TS (Opt+Freq with calcfc). |
Practice: Cope Rearrangement
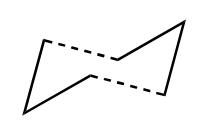
The classic example of a Cope rearrangement is the [3,3]-sigmatropic rearrangement of 1,5-hexadiene. Its mechanism has been debated for a long time (stepwise/dissociative/concerted) but it is now accepted that it rearranges in a concerted, pericyclic fashion via a diradical transition state. This TS bears similarity to either the cyclohexane boat or chair conformation:
|
| |
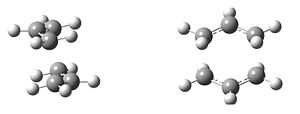
|
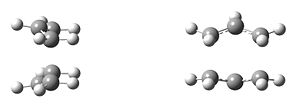
| |
| Chair Transition State | Boat Transition State |
Note that reoptimising from these steps works well as they are unimolecular. When there are two or more reactants, an optimisation becomes very difficult as the PES is bumpy and the gradients are small. This can yield reactants that are irrelevant to the reaction. Usually you can calculate the reactants separately, with the assumption that they react from infinite separation. |
Method 2
Advantages: Fastest reliable method Disadvantages: Requires knowledge of the TS This method requires drawing a guess TS structure and freezing the atoms directly involved in the reaction. Freezing atoms prevents them from moving, and the rest of the system is allowed to minimise. This ensures the system is as close as possible to the TS before the actual optimisation.
Step 2: Freeze the distances between the atoms involved in the reaction (note that GaussView and Gaussian refer to these distances as 'bonds' even though they might not be 'bonded'). To do this, click on 'Edit' then Redundant Coordinate Editor. On the molecular editor window, select the atoms of a bond to freeze. Go back to the Redundant Coordinate Editor and change 'Unidentified' to 'Bond', 'Add' to 'Freeze'. For each atom pair, you need to add a coordinate. Before closing the window, make sure there are no errors (shown at the bottom of the window) and that the correct pairs are frozen. Step 3: Set up the calculation. You should notice that the keywords line now contains opt=modredundant. Submit as normal (optimise to a minimum, not a TS). Force constants are not required. Step 4: When the job has terminated successfully, open the log file in GaussView. Check that the frozen 'bonds' have remained the same length. Now copy this geometry into a new window and follow Steps 2-4 of Method 1. Ensure that frozen bonds are removed in the TS calculation. Gaussian will behave unpredictably if you attempt to search for a TS with bonds still frozen. |
Practice: Cyclopentadiene Dimerisation
Familiarise yourself with Method 1 before attempting this exercise
If you've used cyclopentadiene in the lab, chances are you've needed to 'crack' it. The reason for this is that cyclopentadiene dimerises with a half-life of hours at room temperature, or more slowly at lower temperatures. This dimerisation is an example of a Diels Alder reaction. Cracking is the process of heating it to reverse the reaction back to the reactive monomer. This is due to the negative entropy of the reaction that disfavours dissociation, which becomes more significant at higher temperatures.
|
Method 3
Advantages: More reliable than previous methods. Doesn't require much knowledge of the TS. Disadvantages: Requires additional steps. Difficult if minima are far away in geometry from TS. There can be problems if you start from the products but your TS resembles the minima. This requires starting from either the reactants and products, and changing bond lengths to resemble the TS.
Step 2: Decide which lengths and/or angles will change during the reaction. Modify them using the appropriate editing tools. Often it's enough to just change the atoms directly involved in the reaction, but if this doesn't work, try altering neighbouring atoms to reflect the change in hybridisation they might undergo. In a classic Diels Alder reaction, for example, 3 double bonds become single bonds and one single bond becomes a double bond, so it might be worth changing these values to somewhere in between. The dienophile carbon atoms become sp3 hybridised, so the neighbouring atoms might need to be distorted a little to reflect this. Step 3: Follow Steps 2-4 of Method 2. |
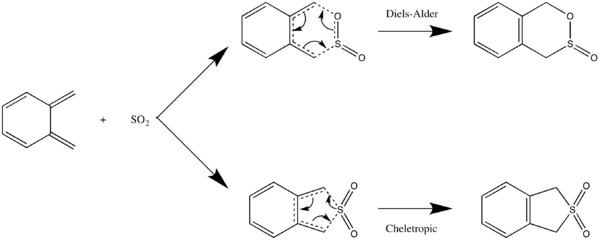
Practice: Xylylene-SO2 Diels Alder Cycloaddition
This is an example of a hetero-Diels Alder reaction, where SO2 is used as a dienophile. Without knowing the direction of approach of the SO2 or whether the barrier is early or late, it can be difficult to use Method 1 or 2. Therefore we'll start from the product.
|
Summary of Methods
Below is a flowchart summarising the 3 methods described above. Note that the green "Calculation" boxes show an example of the preview keywords line (shown at the top of the Gaussian Calculation Setup window) and exclude the method, basis set etc.
Appendix
Analysing the TS
Convergence
Check that the job has properly converged. For each step in optimisation, the gradient will be calculated to determine if the system is at a stationary point. To prove that a stationary point has been found, open the log file and scroll from the bottom to find a section that looks like this:
Item Value Threshold Converged?
Maximum Force 0.000098 0.000450 YES
RMS Force 0.000010 0.000300 YES
Maximum Displacement 0.001379 0.001800 YES
RMS Displacement 0.000379 0.001200 YES
Predicted change in Energy=-4.942954D-08
Optimization completed.
-- Stationary point found.
This job has landed on a stationary point. Compare to the following, which did not converge properly:
Item Value Threshold Converged? Maximum Force 0.000155 0.000450 YES RMS Force 0.000021 0.000300 YES Maximum Displacement 0.002340 0.001800 NO RMS Displacement 0.000561 0.001200 YES Predicted change in Energy=-2.681147D-07
Frequency Calculation
If you haven't already done so, run a frequency calculation on the job (remember to hold parameters the same - method, basis set, solvation etc). Check that you have one vibration and that it corresponds to the reaction by visualising the vibration (Results, Display Vibrations). This is a very good indication that you have the correct transition state structure.
IRC
From a successful vibration calculation (1 negative frequency that corresponds to the reaction), an Intrinsic Reaction Coordinate calculation may be set up. An IRC follows the minimum energy pathway to reactants and/or products on the PES. For a symmetric TS, it's wasted effort to perform the calculation in both directions, so this option can be changed to 'Forward only'. The next option is to calculate force constants. These are required as you'll be starting on a stationary point and the gradient alone isn't enough. Choosing Always can be used for difficult PESs.
By default, Gaussian will take 10 steps down the PES, but this often isn't enough, so choose a higher number such as 200 (note that Gaussian will stop once converged, so if you're seeking convergence, any number larger than the number of steps it takes to converge is fine).
These calculations take a long time if you use an expensive method and basis set (such as B3LYP/6-31G(d) ) while calculating force constants.
As this calculation - and similarly for a frequency calculation - operates on the PES, it must be calculated using the same method and basis set as the optimised TS geometry that it starts with. For example, if you want an IRC for PM6, use the PM6 TS.
Gaussian will often produce an IRC that seems reversed. This is normal and is the result of not providing information as to what the reactants and products are. It can be corrected by identifying a bond that will lengthen over the course of the reaction, for example a bond breaking, or a double bond becoming a single bond. Once the two atoms (N1 and N2) are identified, include this line in the IRC calculation replacing N1 and N2 with the atom numbers:
irc=(phase=(N1,N2))
| Example IRC | Notes/Solutions for errors |
|---|---|

|
A successful, asymmetric IRC.
Note that the gradient must be 0 at the TS, reactants and products (minima). |

|
Failed IRC as the initial geometry is not a TS.
This can happen when the method and/or basis sets are not consistent between the TS and IRC calculation. |
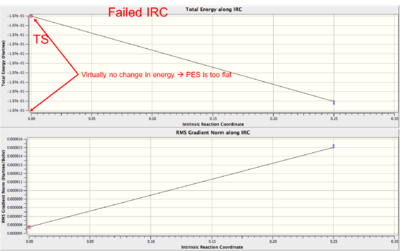
|
Failed IRC as the PES is too flat at the TS and the algorithm cannot decide which direction to move down.
See this page for a fix. |

|
Failed IRC at the first or last point on the IRC. The gradient is 0 here, but it fails as it is not a minimum.
See this page for a fix. |
Reaction Barriers and Reaction Energies
Barriers and reaction energies can be calculated at room temperature and 0K using information from the log file of a frequency calculation. You will need to run a frequency calculation for each of the optimised reactants, TS and products. Using Notepad or Notepad++, open each log file and search for a section named "Thermochemistry".
For 0K, the value to use is the "Sum of electronic and zero-point Energies".
For room temperature, the value to use is the "Sum of electronic and thermal Free Energies".
Useful Tips and information
Comparing results of jobs
When comparing energies between structures, it's important to ensure that the energies are calculated in the same way. In every case, make sure the computational method, basis set, solvation method, convergence criteria and grid are the same. This means if you are using "int=grid=ultrafine" or "opt=tight" in one calculation, it must be used in all calculations for structures that are being compared.
Bond types are ignored by Gaussian
In a quantum mechanical calculation, all Gaussian uses from the geometry is the distances between the atoms. This means specifying a bond type is meaningless and mostly aesthetic - it won't remove two hydrogens if you change a single bond to a double bond. However, they are very important in a molecular mechanical calculation! Check that the number of atoms is correct in all calculations.
Job Monitoring
For jobs that are expected to take a long time or are taking longer than expected, it's worth opening them in GaussView to see how they are doing. In GaussView, choose File then Open. Locate the log file of the job you want to monitor and make sure 'Read Intermediate Geometries is selected and open the file. Now you can periodically refresh the job with File, Refresh. Check that the job looks like it's converging to the correct geometry.
Creating a follow-up job manually
If a checkpoint file (.chk) exists for a file, Gaussian can read the output of it as the input of a new calculation. This has numerous advantages:
- A step in generating the guess wavefunction can be skipped (it's taken from the previous job)
- Force constants can be read into calculations such as IRCs
- Easier to be consistent between calculations
- Additional features, such as restarting previously failed calculations
The drawback is that it's much harder to get used to than GaussView. The general structure of a follow-up input file is:
%mem=<memory> %nprocshared=<processors> %oldchk=<old checkpoint path> %chk=<new checkpoint path> # <keywords> guess=read geom=allcheck <NEWLINE>
Note that all Gaussian inputs must finish with a new line - the parser will read sections until it encounters a newline character, and finish if it reaches the end of a file.
Create the file using Notepad ++. For the memory, choose 1GB to begin with. You might need more if the program runs out of memory. For processors, choose the number of physical processors that you want to run on, which will be up to 4 for the Windows computers. Direct %oldchk to the path of the checkpoint file you want to read from. Note that it should be an absolute path. Input the keywords as required. Save the file with the extension '.gjf'. In an Explorer window, drag the file into an instance of G09 and click Run.
Restarting failed jobs
Sometimes optimisations or IRC calculations fail for a variety of reasons. Create a follow-up input file. If you need to restart an optimisation, add into the keywords opt=restart, or for an IRC, add IRC=restart. Note that if the keywords opt or IRC already exist, you'll need to add restart into the existing keywords.
Troubleshooting
If you encounter errors or problems with any part of this lab, feel free to discuss them with any of the demonstrators. If a demonstrator isn't around, see this link for Gaussian troubleshooting.