Henry Rickard, Yr 2. Submission for Molecular Reaction Dynamics 2nd year computational lab.

Questions in bold quoted directly from the provided script.

Exercise 1: H + H₂ system

On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?

On the potential energy surface, the transition state is defined as the maximum on the minimum energy path across the surface. Being a point that is a local maximum on one axis and a local minimum on another, it can be described as a saddle point on the surface, distinguished from a local minimum by the fact it is also a maximum in one direction on the surface.

A minimal, but acceptable definition. Fdp18 (talk) 20:11, 20 May 2019 (BST)

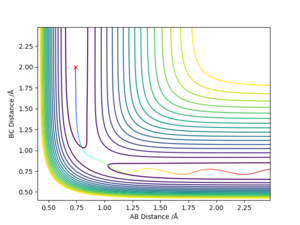
Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

r_ts ≈ {0.908,0.908}

Setting parameters "AB distance = 1, BC distance = 1"

Exporting the data and finding the state of maximum total kinetic energy (minimum potential in the path the system oscillates along) gives a small range of time-steps with different AB/BC distances due to rounding. Taking the mean of these distances gives 0.908 Å for the distance between each pair of atoms in the transition state, and hence the stated r_ts value. This concurs with the internuclear distance-time graph, where it is visible that the average for the A-C distance is slightly over 1.8 Å.

Interesting approach - you are swinging just at the 'edge of the mountain pass'. As a next step, you could start with your averaged values and see if the oscillations disappear. Fdp18 (talk) 20:13, 20 May 2019 (BST)

Comment on how the mep and the trajectory you just calculated differ.

The mep is a smooth line following the floor of the potential valley, whereas the trajectory taking account of dynamics shows the slight oscillation induced by the specified offset from the transition state. This makes sense, because the mep calculation does not conserve kinetic energy and aims to reach a minimum of potential (the valley floor), whereas the dynamics simulation does conserve the introduced small difference in total energy (from minimum potential), and shows the resulting periodic gain and loss of potential energy due to the osciallation of particles.

Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?

All with initial conditions:

AB Distance = 0.74

BC Distance = 2.0

p(AB)	p(BC)	E_tot	Reactive?	Description of the dynamics
-1.25	-2.5	-99.019	Yes	(AB) pair approach C, slow almost to a stop as A-B distance increase and B-C distance decreases. A then moves away from (BC), latter vibrating slightly.
-1.5	-2.0	-100.456	No	(AB) pair approach C, slowing down. Slow almost to stop, then (AB) and C both reverse direction and move away from each other.
-1.5	-2.5	-98.956	Yes	Very similar to the first reaction in this table.
-2.5	-5.0	-84.956	No	(AB) approach C quickly. B immediately associates with C, A moves away, but slows. (BC) oscillate strongly once, while A reverses direction. B then re-associates with A, and (AB) and C seperate again. (AB) vibrating strongly.
-2.5	-5.2	-83.416	Yes	Similar to above, but after B re-associating with A, it also oscillates strongly once before B associates with C again. A and (BC) seperate, with (BC) vibrating strongly.

State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

Transition State Theory (TST) assumes that in a chemical reaction, the trajectory described by the movements of the reacting species passes through a saddle point of potential energy (or the small region surrounding it) between the local minima describing the reactant and product states. The reactants must have enough total energy to overcome the barrier created by this saddle point for the interaction to be reactive and reach the product state.

You seem to have used your own words, which I highly appreciate. However, it would be nice to have the other statements of transition state theory - maybe together with a reference. Fdp18 (talk) 20:17, 20 May 2019 (BST)

For the first three reaction trajectories above, this works relatively well: the 1st and 3rd apparently have a greater (more positive) total energy than is required to reach the transition state and can reach the products (with "left over" energy remaining as vibrational energy in the diatomic product), while the 2nd does not have enough energy and so can not pass through the transition state to the products. For these, it may be expected that TST predictions should match well with experiment. However, for the 4th and 5th trajectories the theory is less successful. While they apparently do have enough energy to reach the transition state, they in fact surpass it and the trajectory is much less predictable. This is observed as a complicated pattern of the products reforming and breaking up again. This could be caused by these trajectories breaking the assumption of the reaction passing through the saddle point region of potential, and so the simple TST is less useful. For these reactions with a large amount of excess energy, TST-based predicitons will likely agreely more poorly with experiement.

Exercise 2: F-H-H system

By inspecting the potential energy surfaces, classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

Given that the F + H₂state is lower in energy than the H + HF state, the direction

F + H₂→ H + HF would be exothermic, and the reverse will be endothermic.

This corresponds to the H-F bond being stronger than the H-H bond, with the stabilisation gained from forming the former being greater than that lost by breaking the latter.

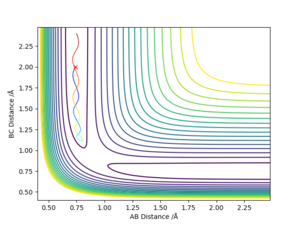
Locate the approximate position of the transition state.

A=B=H, C=F

Finally someone who defines what is what. Fdp18 (talk) 20:19, 20 May 2019 (BST)

Determined by analysing meps to find the 'direction' in which a pair of positions will result in (with the point seperating forward and reverse being the transition state), and the point approaching by the mep as part of the aforementioned analysis from a position of slightly elevated potential near it.

Distance AB = 0.7449 Å

Distance BC = 1.8094 Å

Report the activation energy for both reactions.

Describing F + H₂→ H + HF as the forward reaction:

E_ts= -103.75 units

...and what are these units? Fdp18 (talk) 20:25, 20 May 2019 (BST)

E(H+HF) = -133.92 units (Left equilibrating for 7500 steps at 0.02 units per step)

E(F+H₂) = -104.01 units (Left equilibrating for 100000 steps at 0.02 units per step)

E(forward activation) = 0.26 units

E(reverse activation) = 30.17 units

Calculating by performing an mep from a position slightly offset from the transition state on the side of the minimum being examined, and leaving to ‘equilibrate’ for a significant amount of time. The reactant required a very large amount of time to do so because the potential gradient between that local minimum and the saddle point (the reactants and the transition state) was extremely low.

Below are the graph used to establish these values. The whole plots are shown, although zooming in was used to determine more significant figures than are shown on the axes. Note the different scales on the energy-time graphs.

Very clear description of what you did that also shows a lot of understanding of what's going on. Fdp18 (talk) 20:27, 20 May 2019 (BST)

Direction	Contour Plot	Energy-Time Graph
Forward
Reverse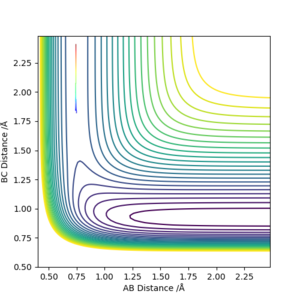

In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.

The difference in potential between the reactants and products is conserved as a change in kinetic energy of the product species; this kinetic energy may be either vibrational or translational. In bulk matter, this would be distributed throughout the reaction mixture as heat. Experimentally, this could be examined by measuring the temperature increase in the gas-phase reaction of fluorine radicals and hydrogen. The practical aspects and exact method of such an experiment would require further investigation than is performed here, but a possible procedure may involve photolytically producing the radical species as the gas was slowly introduced to a hydrogen atmosphere.

It is actually possible to conduct this experiment, and there is a 'practical application' - the hydrogen fluoride laser. Fdp18 (talk) 20:29, 20 May 2019 (BST)

Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

For conditions r(AB)=0.74, r(BC)=2.25, p(BC)=-0.5,

p(AB) = between 2.8499099990 and 2.8499099999 is transition between reactive and non-reactive in the simulation

also betweeen -2.87990 and -2.87995

very complicated association then disciation and reassociation when near transition

How long did it take you to get to that number? Though I appreciate the effort, this is not what was meant. The keyword to look for are Polanyi's principles and late/early transition states. Fdp18 (talk) 20:33, 20 May 2019 (BST)

No references given - these would be necessary when you include the other TST statements. Fdp18 (talk) 20:33, 20 May 2019 (BST)

Exercise 1: H + H2 system

Exercise 2: F-H-H system

Exercise 1: H + H₂ system