CP3MD

The software

Download the zip archive with the software and data files required for this experiment.

Extract the content of the archive and run the lepsgui.py file to start the program. Please see below if you are unable to run the file.

Running from the command line on Windows

Follow the steps:

1. Using the File Explorer navigate to the directory where the program files are.
2. On the File tab on the top of the window select "Open Windows PowerShell".
3. Type python lepsgui.py to run the program.

If the last step fails, there might be an issue with your python installation and the python interpreter is not in your PATH. In that case you will need to type the full path of the python.exe file on your system (if using Anaconda, this may look something like C:\Anaconda3\python.exe).

Running from the Anaconda prompt

If you are unable to get the above to work and are using Anaconda, start the Anaconda prompt from the Anaconda-Navigator. Navigate to the directory where the programs are using the 'cd' and 'ls' commands. On that directory type lepsgui.py.

On macOS or Linux

1. Open a terminal.
2. Using the commands 'cd' and 'ls', navigate to the directory where you extracted the zip archive.
3. Type python lepsgui.py to run the program.

Introduction

Objectives

The objectives of this exercise are to study the reactivity of triatomic systems, where an atom and a diatomic molecule collide, through calculating Molecular Dynamics trajectories.

This exercise is designed to make you think about transition states, reaction coordinates and potential energy surfaces, and how these affect the outcome of chemical reactions. We will be looking at collision and reaction between an atom and diatomic molecule in a linear configuration in the gas phase. If the reaction proceeds, it will form a new diatomic molecule and atom. You should discover that, for a chemical reaction to take place, having sufficient energy to overcome a barrier is not enough: the energy must also be in the right vibrational or translational modes at the right time.

The write-up Required

In this lab you will be writing a report of your results in the form of a wiki. You should explicitly address questions highlighted in blue in the script

and backup your answers with results and illustrations of calculations you perform using the program.

To start your report choose a URL of the form https://wiki.ch.ic.ac.uk/wiki/index.php?title=MRD:anything , insert it on the address bar of the browser and start editing. The URL you choose must be unique. All figure files you upload to the wiki must also have unique names. A good way of generating unique URLs and files names is by adding your CID or college login to them. Do not ignore any wiki warnings about file name clashes.

Using the wiki visual editor should be sufficient to write your report. If you want to edit the source of your wiki some general instructions are available, and you can also search the web.

After some time without saving your work (about 30 min) the wiki system might log you out and you may lose unsaved changes. To avoid this, choose the "Keep me logged in" option when you login or save your work regularly.

Submit the address of your wiki via Blackboard. Only edits completed before the deadline in the week you are scheduled to do the exercise will be considered.

Theory

Introduction

It is possible to simulate a chemical reaction by describing the relative motion of the atoms that occurs while the reaction takes place. Since the mass of the atoms is relatively large (compare with the mass of the electron for example), for many chemical reactions it is possible to assume that the motion of the atoms follow Newton's equations of motion, i.e. obey classical mechanics. This is an approximation, since it neglects the fact that molecular vibrations are quantized or quantum tunneling effects, but it is nevertheless a good approximation for most chemical reactions.

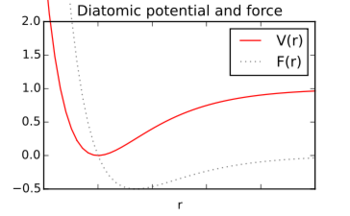
The relative motion of the atoms will depend on the interaction between them, which in turn depends on their relative position (for example, how far their nuclei are from each other). Interatomic interactions, as part of a molecule or not, are expressed as a potential energy surface V(r₁,r₂,...) which represent the potential energy of the system as a function of the atoms' relative positions defined by the different internal coordinates r_i. (For a diatomic molecule V(r) is just the usual potential energy curve that expresses the change in the energy as the two nuclei are displaced from their equilibrium positions by changing the interatomic distance – making the separation too small leads to a rapid rise in potential energy and increasing the bond length also leads to an increase in energy and eventually to dissociation).

Potential energy as a function of the interatomic distance for a diatomic molecule.

The force (variation of momentum p) acting on a given interatomic coordinate r_i will depend on the derivative of the potential energy surface with respect to that coordinate.

$\frac{d{p}_i}{dt}=-\frac{\partial V(r_1,r_2,...)}{\partial r_i}$

By solving the equations of motion we are able to determine the trajectory of the system, i.e. determine the relative position of the atoms at each instant in time r(t). The trajectory represents a path across the potential energy surface (you will see examples shortly), and can be used to gain insight on how the reaction might proceed.

Such simulations have many applications in chemistry and biology and you may well encounter these in higher level lecture courses in year 4.

Note that the program does all these calculations for you. You input bond distances and momenta for the atoms specified and the potential energy surface and the trajectory the system follows across the surface is calculated for you. Your job is to interpret the results.

Atom-Diatom Collisions

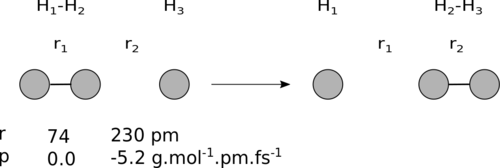
In this exercise we will apply this method to study atom diatom collisions. A typical example is depicted below.

In simple terms, the atom m₁ collides with the molecule and forms a new molecule with m₂, while m₃ is detached as a separate atom. 

If we think about how the distances r₁ and r₂ change during this process we can make several deductions. 

Before the collision/reaction:

• r₂ will be approximately constant (it will oscillate slightly if the molecule has vibrational energy).
• r₁ is decreasing steadily as m₁ gets closer to m₂.

After the collision/reaction:

• r₁ will now be approximately constant (but it will oscillate slightly if the molecule has vibrational energy).
• r₂ is increasing steadily as m₃ moves away from the molecule formed from m₂  and m_1.

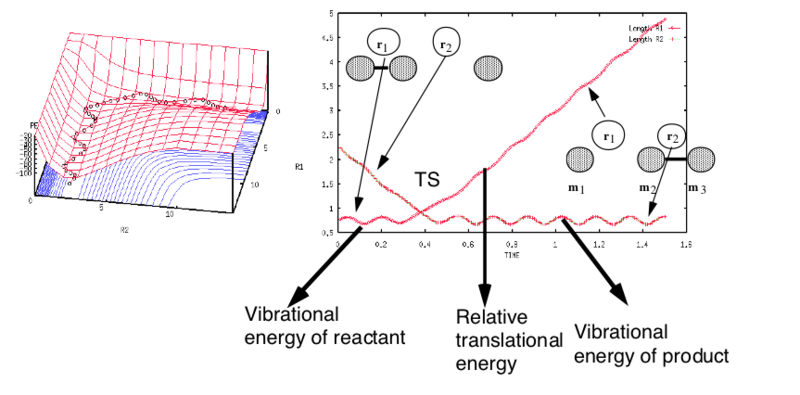
This means that instead of our simple picture of energy versus reaction coordinate we can map the progress of this reaction on a potential energy surface where potential energy is plotted as a function of both r₁ and r₂. A trajectory {r₁(t) r₂(t)} can then be drawn on this potential energy surface. In a first instance, one can think of this trajectory in terms of that a sphere rolling of potential energy shaped surface would follow. However this analogy in the r₁ and r₂ coordinates is not accurate, as the system is not really formed by a single rolling mass but several interacting masses. (As will be discussed further below, the rolling sphere analogy can be made accurate via a change of coordinates which distort the potential energy surfaces.)

An example of a reactive trajectory for an H + H₂ type potential surface. The small boxes indicate the reactants (r₁ large r₂ small), a transition structure where r₁=r₂, and the products (r₁ small r₂ large). (Note that the variation of potential energy along the combined r₂ and r₁ axes is the typical reaction profile curve you have seen before).

The general triatomic system depicted means we started with atom A and molecule BC and ended with molecule AB and atom C. A reactive trajectory that passes through the transition structure is shown as a wavy line. The transition structure is a saddle point in the potential energy surface. Notice that the trajectory shown involves vibration in r₂ (the molecule BC has vibrational energy) as the inter-fragment distance r₁ is decreased in the entrance channel (at the top left of the figure) and vibration in r₁ (the product AB has vibrational energy) as the inter-fragment distance r₂ is increased in the exit channel (at the right of the figure). An unreactive trajectory would bounce off the barrier or its surroundings and regenerate the reactants.   

For a given potential surface, the outcome of a dynamics simulation (i.e. the positions r₁(t), r₂(t) and the momenta p₁(t), p₂(t)) at some time t are determined by the initial conditions at time t=0 (i.e. r₁(0), r₂(0) and the momenta p₁(0), p₂(0)).

In the program you will use, you will run trajectories on different potential surfaces - corresponding to different triatomic chemical systems - for a variety of input conditions.  You will be able to animate the trajectory on the potential surface and examine the distribution of vibrational and translational energy in the products. 

You will first study the potential surface for an atom of H colliding with a molecule of hydrogen to illustrate the principles and to learn how to use the main features of the program. You will then move to look at other reaction examples.

EXERCISE 1: H + H₂ system

Before you begin experimenting with the different types of collision, note that the script makes reference to r₁ and r₂ whereas in the GUI the atoms are currently labelled A B and C and the distances are r_AB and r_BC. Since you run some trajectories in both forward and reverse directions it is hard to develop a consistent notation. Thus before you run a trajectory, check carefully what you have set up. Your initial molecule will be defined by which of the AB or BC distances you have set to be the bond distance. One distance will be short (the bond distance) and one will be long. 

Running and visualising a trajectory

In this part you are given a set of conditions such that the reaction depicted below will proceed.

We first set up the calculation of how the atoms position and momenta change with time, and then we will analyse the results of this calculation

The program has a set of initial conditions and will run with those when you first run lepsgui.py and should show you a contour plot.

• Change the initial condition in the settings window to run the example above: check the initial conditions that are shown in the menu agree with the figure (r₁(0) = 74 pm  r₂(0) = 230 pm  and the momenta p₁(0) = 0 g.mol^-1.pm.fs^-1 p₂(0) = -5.2 g.mol^-1.pm.fs^-1).

For p₁= = 0 g.mol^-1.pm.fs^-1, a negative value of p₂ corresponds to a decrease in the interatomic distance r₂.  By choosing these initial conditions, we are thus setting the system in motion in such a way as to initially decrease r₂ (refer to the diagram above).

In this case BC is the molecule with a bond distance = 74 pm and A is the atom that collides with it. Thus here r₁ = r_BC.

These initial conditions of the positions and momenta produce a reactive trajectory (like the example above). In other words, these conditions lead to the reaction taking place. As you will see in later sections, not all trajectories you run will be reactive.

The program updates the image on the separate dedicated window when you press the “Update Plot” button at the bottom left of the settings window. By default the program will show you the trajectory corresponding to the input initial conditions and the contour plot of the Potential Energy Surface (PES). To see other plots, such as plots of positions and momenta against time, or a 3D surface plot of the reaction, select that option from the "Plot Type" menu at the centre of the interface and press "Update Plot". Spend some time to have a look at the various options:

• Selecting "Skew Plot" will produce a potential energy contour plot on a different set of coordinates Q₁ and Q₂, where the oblique mesh defines the direction of the coordinates r_AB and r_BC. The new coordinates are defined as:

$$\begin{gathered} \begin{array}{rl}& Q_1=\sqrt{{\mu }_{A,BC}} \\ {r}_{BC}+\sqrt{{\mu }_{C,AB}} \\ {r}_{AB}\cos (\beta )\\ & Q_2=\sqrt{{\mu }_{C,AB}} \\ {r}_{AB}\sin (\beta )\end{array} \end{gathered}$$

with

$\begin{array}{rl}& {\mu }_{A,BC}=\frac{m_A(m_B+m_C)}{m_A+m_B+m_C}\\ & {\mu }_{C,AB}=\frac{m_C(m_A+m_B)}{m_A+m_B+m_C}\\ & {\cos }^2(\beta )=\frac{m_A{m}_C}{(m_A+m_B)(m_B+m_C)}\end{array}$

where β is the so called Skew angle setting the angle of the oblique mesh. The advantage of this set of coordinates is that the dynamics of the system can be analysed as a rolling sphere on a potential surface, where the force acting on the trajectory is orthogonal to the contour lines. (If you are interested in the details, check the further reading section.)

• Select “Surface Plot”, which gives you a plot of the PES in the r₁ and r₂ coordinates. You can have a better look at the surface plot by rotating it with the mouse. Try to identify the reactant and product channels and the maximum potential energy along the valley floor. The trail of black dots along the bottom of the potential is the trajectory followed by the system. Observe how the trajectory is wavy: this indicates that the diatomic molecule is vibrating. An important point to observe is conservation of energy: the system will always oscillate between energy contours with the same value.

• To animate the geometry, select the last option, “Animation”, in the "Plot Type" menu. You will see that initially r₂ decreases as H₃ approaches H₁-H₂, then after the transition state, H₁ leaves and H₂-H₃ is formed in a vibrationally excited state.

• This same information can be displayed in a different form by selecting “Internuclear Distances vs Time” in the same menu. In this graphical display the values of r₁(t), r₂(t) are given (Y axis) against time t (X axis). Notice that r₂ (r_AB here) decreases from the original value of 230 pm during the first 30 fs, then it has an oscillatory behaviour for the remainder of the trajectory corresponding to H₂-H₃ vibration.  In contrast r₁ (r_BC here) has a slight oscillatory behaviour initially, then after the transition state, it grows in value as H₁ leaves. Notice that r₁(t) = r₂(t) at ≈ 25 fs, and in this case is quite close to the transition state structure (this is not the case for all trajectories).

r₁(t) and r₂(t) are given (Y axis) against time t (X axis). Note that only two distances are shown on this plot. The GUI shows three.

• The "Internuclear velocities vs Time" option shows how the internuclear distances are changing in time (i.e. their velocity). An oscillation around zero corresponds to a vibration, while average positive or negative values correspond to two atoms distancing or approach each other respectively.

• Next, select “Energy vs Time” in the same menu.  It will show an oscillatory behaviour rising in energy until the transition state is reached. The potential energy then falls as the trajectory moves into the product / exit channel. The energy is continually switching from potential energy to kinetic energy during the trajectory. Total energy should be conserved, so if you see a decay in the total energy try using a smaller time step. At the turning point of a trajectory, one is at the maxima of the oscillations. At the bottom of the trough of the oscillations the potential energy is low and the molecule is moving faster so the energy has gone into kinetic energy. In this case the kinetic energy reaches its minimum value at the transition state.

• Finally the momenta p₁(t) and p₂(t),  can be displayed using “Momenta vs Time”. This result is not so easy to interpret because the momenta correspond to bond stretching displacements r₁ and r₂ , not the momenta of the atoms themselves.

Thus p₁ is the momentum in the coordinate r₁. Notice that the momentum in the atom 2 results from both momenta p₁ and p₂.   Thus if we want to collide atom 3 with 1-2 (by giving some p₂) in such a way that the diatom 1-2 does not vibrate, we must give some momentum in p₁ as well. Following the momentum distribution approaching transition state region and then distancing from it, provides some insight on the distribution of the kinetic energy on the different motions of the system, as we now discuss.

Initially p₁(0)= = 0 g.mol^-1.pm.fs^-1 and p₂(0)= = -5.2 g.mol^-1.pm.fs^-1.  At the beginning of the trajectory p₂(t) decreases in absolute value and p₁(t) takes on an oscillatory behaviour. p₁(t) oscillates because the initial momentum in p₂ also forces r₁ to change as shown by the picture above. After the reaching the transition state at t= 25 fs, p₁(t) rises rapidly and remains constant (corresponding to translation) as r₁ becomes large as H₁ leaves.  In contrast p₂ initially corresponds to translation. After the transition state p₂ oscillates (corresponding to vibration).           

Dynamics from the transition state region

Gradients at the transition state, as well as in the reactants and product regions.

The transition state is defined as the maximum on the minimum energy path linking reactants and the products. This point on the potential energy surface has the special property that ∂V(r_i)/∂r_i=0 (the gradient of the potential is zero), and the energy goes down most steeply along the minimum energy path linking reactants and products. Consequently, if one starts a trajectory exactly at the transition state, with no initial momentum, it will remain there forever.  However, if one changes the geometry by a small amount in the direction of the products it will roll towards the products (and similarly for the reactants).  One way of locating the transition state is to start trajectories near the transition state and see whether they "roll" towards the reactants or products.

On a potential energy surface diagram, how is the transition state mathematically defined? How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?

Trajectories from r₁ = r₂: locating the transition state

Since the H + H₂ surface is symmetric, the transition state must have r₁ = r₂. If we start a trajectory on the ridge r₁ = r₂ there is no gradient in the direction at right angles to the ridge, thus the trajectory will oscillate on the ridge and never fall off. This fact can be used to locate the TS geometry.

• Locate the transition state of the reactions by testing different initial conditions with r₁ = r₂, and p₁ = p₂ = 0.0 g.mol^-1.pm.fs^-1.

If you select “Animation” mode, you should see that the system undergoes a periodic symmetric vibration.

Report your best estimate of the transition state position (r_ts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectory.

Calculating the reaction path

The reaction path (minimum energy path or mep) is a very special trajectory that corresponds to infinitely slow motion (i.e. the momenta/velocities are always reset to zero in each time step). Once the transition state has been located, one may run the very special “trajectory” that corresponds to the mep.

• Set the initial conditions such that the system is slightly displaced from the transition state and zero initial momenta (i.e. the positions r₁ = r_ts+1 pm,  r₂ = r_ts and the momenta p₁ = p₂ = 0 g.mol^-1.pm.fs^-1), then change the calculation type from dynamics to MEP (you may need to increase the number and/or size of steps to obtain a complete mep).

You will see that the trajectory simply follows the valley floor to H₁+ H₂-H₃.

Trajectories from r₁ = r_ts+δ, r₂ = r_ts

While the mep is useful to characterise a reaction, it doesn't provide a realistic account of the motion of atoms during a reaction. Atoms have mass and in the gas phase (as we are studying here) their motion will be inertial.

• Repeat the calculation with the same initial conditions used to calculate the reaction path, but change the calculation type back to Dynamics.

Comment on how the mep and the trajectory you just calculated differ.

Look at the “Internuclear Distances vs Time” and “Momenta vs Time”. What would change if we used the initial conditions r₁ = r_ts and r₂ = r_ts+1 pm instead?

Take note of the final values of the positions r₁(t) r₂(t) and  p₁(t) p₂(t) for your trajectory for large enough t.

• Setup a calculation where the initial positions correspond to the final positions of the trajectory you calculated above, the same final momenta values but with their signs reversed.

What do you observe?

Reactive and unreactive trajectories 

Is there a general way to determine the conditions for a reactive trajectory that starts in the region of the reactants and passes near the TS region? From the previous calculations we can conclude that trajectories with initial conditions in the range r₁ =74 pm, r₂ = 200 pm, with -3.1 < p₁/ g.mol^-1.pm.fs^-1 < -1.6 and p₂ = -5.1 g.mol^-1.pm.fs^-1 are reactive (you can run trajectories yourself to confirm this statement). It would seem fair to assume that all trajectories starting with the same positions but with higher values of momenta (higher kinetic energy) would be reactive, as they have enough kinetic energy to overcome the activation barrier. Let us test this hypothesis.

• For the initial positions r₁ = 74 pm and r₂ = 200 pm, run trajectories with the following momenta combination and complete the table.

p1/ g.mol-1.pm.fs-1	p2/ g.mol-1.pm.fs-1	Etot	Reactive?	Description of the dynamics	Illustration of the trajectory
-2.56	-5.1
-3.1	-4.1
-3.1	-5.1
-5.1	-10.1
-5.1	-10.6

Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?

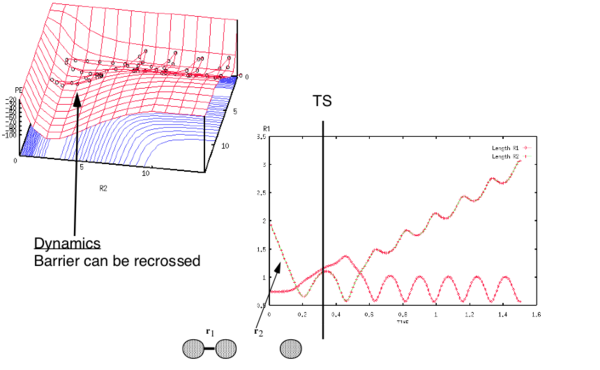
The penultimate set of conditions illustrates a case of barrier recrossing. The system crosses the transition state region, you should see the bond in the product actually forms (see “Animation”) but then the system reverts back to the reactants.

Trajectory that re-crosses the TS region

Transition State Theory

A powerful theory to rationalise and calculate the rate of chemical reactions based on the properties of the reactants and the transitions state structure is Transition State Theory (see further reading section). It predicts that the rate constant for a generic bimolecular reaction ${𝒜}{+}{ℬ}\to {𝒫}$ is

$k_{TST}=R_{cl}\frac{{Q_{{‡}^{\prime }}}^{\prime }/V}{(Q_{{𝒜}}/V)(Q_{{ℬ}}/V)}{e}^{-\frac{E_0}{k_{B}T}}$,

where V is the volume of the macroscopic system, $Q_{{𝒜}}$ and $Q_{{ℬ}}$ are the partition functions of the reactants (they may include translational, rotational, and vibrational components as appropriate. The electronic partition function is equal to 1.) ${Q_{{‡}^{\prime }}}^{\prime }$ is the partition function of the transition state structure, but where the vibrational component includes all coordinates orthogonal to the mep (in our case the symmetric vibration), but not the motion along the reaction coordinate/mep. E₀ is the activation energy.

R_cl is the average transmission rate/frequency with witch trajectories in the reactants side of the potential energy surface reach the dividing surface that passes through the transition state and is orthogonal to the reaction coordinate/mep, and nominally divides reactants and products. A crucial assumption of Transition State Theory in estimating R_cl is that all trajectories with a kinetic energy along the reaction coordinate greater than the activation energy will be reactive. By further assuming that the kinetic energy along the reaction coordinate follows the Boltzmann distribution, one obtain the conventional Transition State Theory rate constant expression:

$k_{TST}=\frac{k_{B}T}{h}\frac{{Q_{{‡}^{\prime }}}^{\prime }/V}{(Q_{{𝒜}}/V)(Q_{{ℬ}}/V)}{e}^{-\frac{E_0}{k_{B}T}}$,

where h is Planck's constant. Energy quantisation can be taken into account when calculating the partition functions, and differences between vibrational zero-point energies for reactants and transition state can be included in calculating E₀, but in Transition State Theory the motion of the system over the barrier, along the reaction coordinate, is considered classically (i.e. it is described by a trajectory with a velocity, not by a wavefunction).

Note that unlike in the Arrhenius equation, in Transition State Theory the pre-exponential factor depends on temperature, both via R_cl and the partition functions.

Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?

EXERCISE 2: F - H - H system

Select the F - H - H potential surface by changing the atom types in the GUI.

PES inspection

By inspecting the potential energy surfaces, classify the F + H₂ and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?

Locate the approximate position of the transition state.

Because the activation energy for one of the reactions is so small, it is not easy to locate the transition state immediately. Use the Hammond postulate to guide your search.

Report the activation energy for both reactions.

You will be able to report a reasonable estimate by performing a mep (with a sufficient number of steps) from a structure neighbouring the transition state, and choosing to plot the appropriate quantity as a function of "time".

Reaction dynamics

• Identify a set of initial conditions that results in a reactive trajectory for the F + H₂, and look at the “Animation” and “Momenta vs Time”. In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. Explain how this could be confirmed experimentally.

• Setup a calculation starting on the side of the reactants of F + H₂, at the bottom of the well r_HH = 74 pm, with a momentum p_FH = -1.0 g.mol^-1.pm.fs^-1, and explore several values of p_HH in the range -6.1 to 6.1 g.mol^-1.pm.fs^-1 (explore values also close to these limits). What do you observe? Note that we are putting a significant amount of energy (much more than the activation energy) into the system on the H - H vibration.

• For the same initial position, increase slightly the momentum p_FH = -1.6 g.mol^-1.pm.fs^-1, and considerably reduce the overall energy of the system by reducing the momentum p_HH = 0.2 g.mol^-1.pm.fs^-1. What do you observe now?

Let us now focus on the reverse reaction, H + HF.

• Setup initial conditions starting at the bottom of the entry channel, with very low vibrational motion on on the H - F bond, and an arbitrarily high value of p_HH above the activation energy (an H atom colliding with a high kinetic energy).

• Try to obtain a reactive trajectory by decreasing the momentum of the incoming H atom and increasing the energy of the H - F vibration. (It may be difficult to find the initial conditions that generate a reactive trajectory for this reaction. Using the inversion of momentum procedure for a trajectory starting on the transition state can be useful in this case. Working on the Skew Plot framework could also be helpful.)

The cases studied are an illustration of Polanyi's empirical rules. Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.

Background reading

Note that it is possible to start this exercise and run some trajectories very easily but reference to literature will be needed to understand the concepts introduced.

In the impossibility of browsing these books in the library, copies of sections of the first three references are available on the Leganto reading list.

Kinetics/reaction dynamics references

A good reference about transition state theory is chapter 10 of J. I. Steinfeld, J. S. Francisco, W. L. Hase Chemical Kinetic and Dynamics 2^nd ed., Prentice-Hall, 1998.

• Chapter 10: Statistical Approach to Reaction Dynamics: Transition State Theory
  • 10.1 - Motion on potential energy surfaces
  • 10.2 - Basic postulates and standard derivation of Transition State Theory
  • 10.3 - Dynamical derivation of Transition State Theory
  • 10.10 - Critique of Transition State Theory

Also interesting are sections:

• 9.4.2 - Some general principles concerning energy disposition in chemical reactions (A discussion of Polanyi's rules)
• 8.3.1 - Classical trajectory calculations (A somewhat high level discussion of dynamics and skewed coordinates)

A classic of chemical kinetics, itself with a rich bibliography, is K. J. Laidler Chemical Kinetics 3^rd ed., Harper-Collins, 1987. Most interesting for this experiment are sections

• 4.5 - Conventional Transition-State Theory
• 4.8 - Assumptions and Limitations of Conventional Transition-State Theory
• 12 - Reaction Dynamics
  • 12.3 - Features of Potential-Energy Surfaces (Includes a of Polanyi's rules even if not called by this name.)

This last section discusses in some detail several features of different triatomic reactions. It uses a somewhat confusing vocabulary of "repulsive" or "attractive" surface to refer to late or early transition-state reactions respectively.

A more advanced reference on the topic of molecular reaction dynamics is N. E. Henriksen and F. Y. Hansen Theories of Molecular Reaction Dynamics 2^nd ed., OUP, 2019. Several derivations of the transition state theory rate expressions can be found in the first sections of the chapter

• 6 - Bimolecular Reactions, Transition-State Theory

A somewhat simplified approach can be found in M. J. Pilling, P. W. Seakins Reaction Kinetics, 2^nd ed., OUP, 1995, in particular section:

• 3.4 - Transition State Theory
• 4.4 - Reaction dynamics and potential energy surfaces (with a discussion of skewed coordinates)
• 4.5 - Potential energy surfaces
• 4.6 - Calculation of kinetic properties from potential energy surfaces

A good high level reference for this experiment is D. M. Hirst Potential Energy Surfaces: Molecular Structure and Reaction Dynamics Taylor and Francis, 1985, in particular section:

• 6.3 - The relationship between reaction dynamics and potential surface (includes some discussion of Polanyi's rules and skewed coordinates)

Also interesting might be:

• 3.1 - Potential hypersurfaces for triatomic molecules
• 3.2 - Correlation diagrams
• 5.4.1 - The London-Eyring-Polanyi-Sato function (a description of the potential energy function we are using)
• 6.2 - Classical trajectory calculations

John C. Polanyi shared the 1986 Nobel prize of Chemistry for his contributions to molecular reaction dynamics, and his Nobel lecture J. C. Polanyi Science 236:680-690 (1987) provides an interesting overview and a summary of the rules that bare his name towards the end of the article.

For a comment on the derivation of Transition State Theory (or Activated Complex Theory) rate constant expressions see B. H. Mahan J. Chem. Educ. 51(11):709 (1974).

General references

Atkins, de Paula, Keeler: Physical Chemistry, 11^th Edition.

• Focus 17: Chemical kinetics
  • Section 17D.2 - The interpretation of Arrhenius parameters
• Focus 18 Reaction dynamics
  • Section 18A.1 Reactive encounters
  • Section 18C.1 The Eyring Equation (The treatment followed here is not the most relevant for the current experiment and can be confusing. You may want to skip this section and search another reference)
  • Section 18D.2 Reactive collisions
  • Section 18D.3 Potential Energy Surfaces (PESs)
  • Section 18D.4 Some results from experiments and calculations

A good reference is I. N. Levine, Physical Chemistry, McGraw-Hill (section numbers are from the 4th edition).

• Chapter 23: Theories of reaction rates
  • 23.2: Potential-Energy Surfaces
  • 23.3: Molecular Reaction Dynamics
  • 23.4: Transition State Theory for Ideal-Gas Reactions

If you don't find the reference above in the library, you can have a look at R. J. Silbey, R. A. Alberty, M. G. Bawendi Physical Chemistry, 4th ed., John Wiley & Sons, 2005.

• Chapter 19: Chemical Dynamics and Photochemistry
  • 19.2: Potential energy surfaces
  • 19.3: Theoretical calculation of a rate constant
  • 19.4: Transition State Theory