MRD:bss15
Molecular Reaction Dynamics
EXERCISE 1: H + H-H system
What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
The total gradient of the potential energy surface at the minimum and transition structure would be zero; however, their position on the graph are different. To distinguish the two points, the 2nd derivative can be looked at.
The 2nd derivative of the minima would be greater than 0 as the minima would be the lowest value on the 'valley' of a graph.
The 2nd derivative of the transition structure would be lower than 0 as the transition structure would be on a 'saddle' and would be the maximum of the minimum energy path; therefore, at the transition structure the trajectory would 'roll down' to either product or reactant depending of the initial conditions of the experiment.
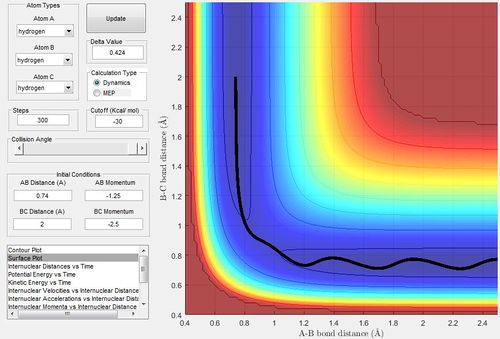
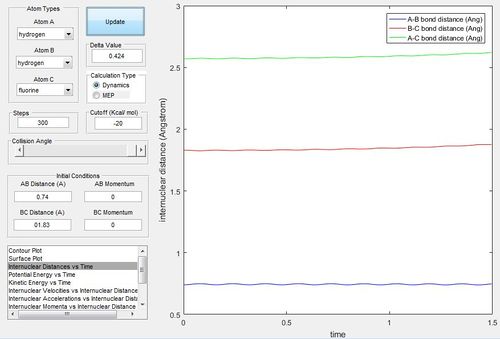
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” screenshot for a relevant trajectory.
The best estimate of the transition state position would be 0.908. As in equal distances, the protons would symmetrically vibrate as they try to achieve the transition structure; however, oscillate due to the momentum to achieve that position. At the transition state position, there would virtually be no vibration.
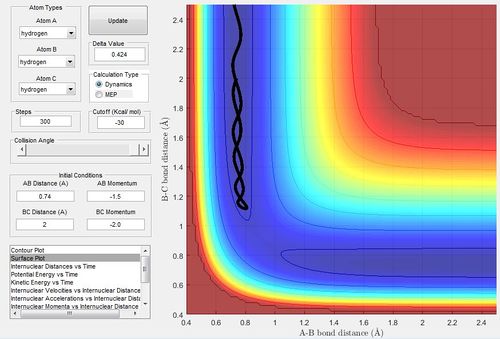
Comment on how the mep and the trajectory you just calculated differ.
The trajectory obtained through dynamic trajectory using (rts+0.01 with rts) would be different from the mep as the mep would give a straight line on the floor while the dynamic trajectory line would give a curvy line. This is because the dynamic trajectory would take into account the molecular interactions of vibrations so would give a curvy line.
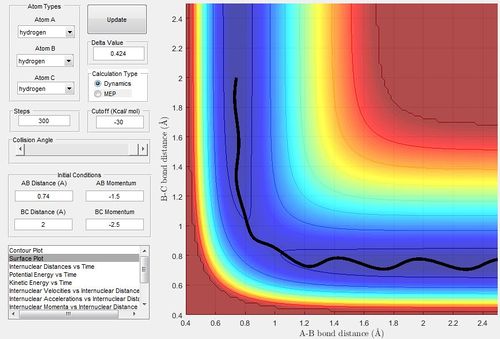
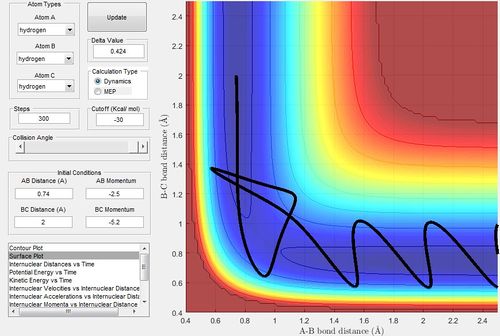
Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.
| Reaction No. | p1 | p2 | Does it React? | Description of Trajectory | Image of Trajectory |
|---|---|---|---|---|---|
| 1 | -1.25 | -2.5 | Yes | reacts successfully with enough momentum and energy to form a bond | 
|
| 2 | -1.5 | -2.0 | No | unable to react and drops back down the valley with excited vibration | 
|
| 3 | -1.5 | -2.5 | Yes | reacts successfully the product is more excited than that of the 1st reaction | 
|
| 4 | -2.5 | -5.0 | No | unreactive despite reaching the transition state region but rolls down towards the reactants | 
|
| 5 | -2.5 | -5.2 | Yes | reacts successfully and after reaching the transition state it deviates from the shape of the valley as the the atoms are highly excited | 
|
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
1) It assumes that the motion of atoms will follow classical mechanisms as the masses are large compared to electrons; therefore, the atoms follow the Newton's Laws.
The assumption ignores the possibilities of quantum tunneling and for reactions with low energy barriers, quantum tunneling would be more present; therefore, experimental values might be higher than TST predictions.
2) It assumes that the trajectory would pass the saddle point.
The assumption might not be true at higher temperatures when the molecules can take higher levels of vibrational modes and cannot estimate more complex systems correctly.
EXERCISE 2: F - H - H system
Classify the F + H-H and H + H-F reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved? Locate the approximate position of the transition state.
The floor of the valley of the graph is different between the two different bonds and the potential energy is lower (floor is lower) when the bond length of H-F is constant. This shows that H-F bond has a stronger bond strength than that of H-H.
Therefore,
F + H-H -> H-F + H is exothermic
H + H-F -> H-H + F is endothermic
rHF = 1.83 with rHH = 0.74 would be the approximate position of transition state.
Report the activation energy for both reactions.
Potential Energy for the Transition State = -103.7kcal/mol
Potential Energy for the H-H / F = -103.8kcal/mol
Potential Energy for the H-F / H = -133.9 kcal/mol
Thusly,
Ea for F + H-H = 0.1kcal/mol
Ea for H + H-F =30.1kcl/mol
Reaction Dynamics
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
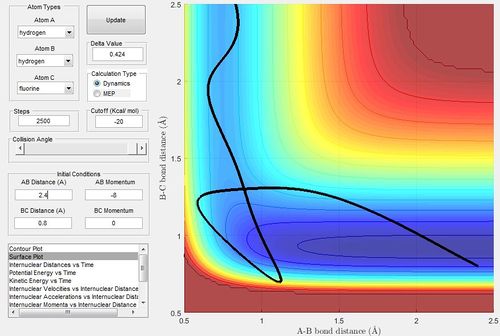
Identify the initial conditions of a reactive trajectory for F + H-H
For Distances,
rHH = 0.74
rHF = 2.30
For Momentum,
pHH = -1.00
pHF = -1.2
but the reaction needs to be observed for a long while (Steps needs to be changed to a higher value 2,500) as the mechanism of forming bonds can take a long while.
The 'Animation' reflects that the complex nature between the momentum, distance and the vibration of the system. It takes a long time on the 'Animation' to actually successfully form the H-F bond.
In the 'Internuclear momenta VS Time' graph, shows that complex interactions between the two bonds. The graph starts off with oscillations of the F against the H-H bond and after some time, it can be seen that the energy is stored in HF as excited high vibrational energy and H having some vibrations to having a straight line (translation). The simulation taking a long time reflects the time it take for the energy to transfer as vibration energy of the H-F bond
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
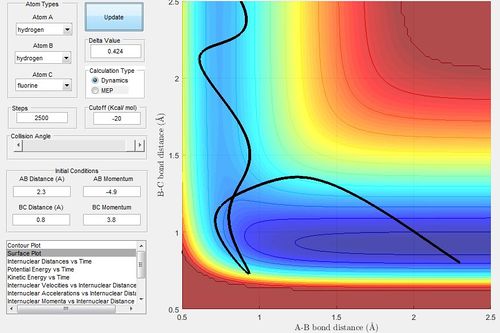
Setting up the initial conditions for the reverse reaction of H + H-F. We can set up different situations which supports the distribution of different modes (translation / vibration).
Set up 1:
Set up 2:
As set up 2 uses a promotes a lower vibrational energy
Polanyi's rules state that translational energy is less efficient than vibrational energy in promoting reactions with late transition states. Using the Hammond's Postulate, a late transition state would reflect endothermic reactions, since the transition state would be closer in energy to the products than the reactants. The conditions above that reflect that.
Thusly,
Set up 1 would require more energy than that of Set up 2.