MRD:YLS15
This report was plagiarised.João (talk) 16:38, 24 May 2017 (BST)
Exercise 1: H + H2 system
What value does the total gradient of the potential energy surface have at a minimum and at a transition structure? Briefly, explain how minima and transition structures can be distinguished using the curvature of the potential energy surface.
The total gradient of the potential energy surface is 0 both at the transition state and the minima. However, these can be distinguished using the value of the second derivatives.
The second derivative of the minima would be greater than zero as the minima is the lowest value on the potential energy surface.
The second derivative of the transition structure of the transition state would be less than zero. It would appear as a characteristic ‘saddle point’ on the potential energy surface.
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with an “Internuclear Distances vs Time” screenshot for a relevant trajectory.
Since the H+H2 surface is symmetric, the transition state must have r1 = r2.
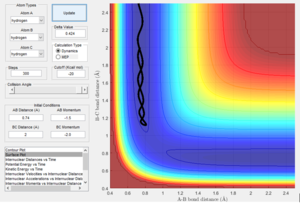
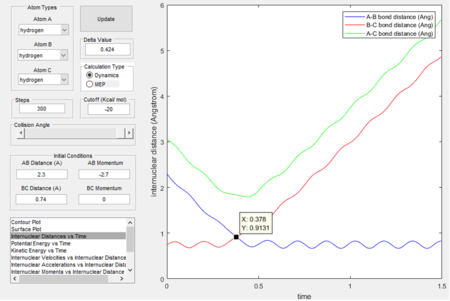
Figure 1 shows as the time goes the 0.378 time units, the internuclear distance rAB and rBC are the same (r1 = r2).
The value of the rts estimated to be 0.9131 Å at this point of intersection.
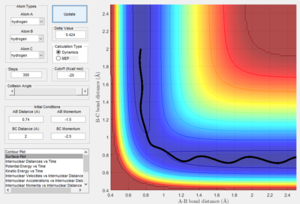
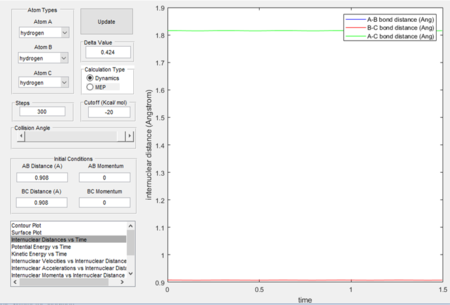
By testing different initial conditions where r1 = r2and p1 = p2 = 0, figure 2 shows the actual value of rts is determined to be 0.908 Å
Comment on how the mep and the trajectory you just calculated differ.
The minimum energy path (mep) always resets its velocity to zero.
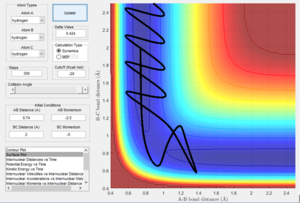
The trajectory follows the minima of the ‘valley’ towards the transition state. This gives a straight line trajectory where as in the dynamics calculations, the vibrational energies are considered so the trajectory by dynamic calculations follow an oscillating path.
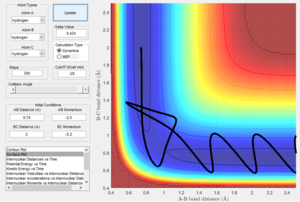
Complete the table by adding a column reporting if the trajectory is reactive or unreactive. For each set of initial conditions, provide a screenshot of the trajectory and a small description for what happens along the trajectory.
State what are the main assumptions of Transition State Theory. Given the results you have obtained, how will Transition State Theory predictions for reaction rate values compare with experimental values?
Transition State Theory assumes that the motion of the atoms follows classical mechanics as the mass of electrons are negligible compared to the atoms. However, this assumption ignores quantum effects such as quantum tunneling.
Exercise 2: F - H - H system
Classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic). How does this relate to the bond strength of the chemical species involved?
The reaction F + H2 is exothermic and H + HF is endothermic as the bond enthalpy of H-F is higher than H-H.
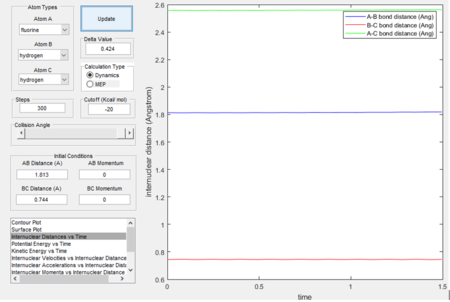
Locate the approximate position of the transition state.
According to Hammond’s postulate, in an exothermic reaction, the transition state resembles the reactants. Therefore, the transition state exists where rH-F = 1.813 Å and rH-H = 0.744 Å which is similar to the bond length of H-H (reactants).
Report the activation energy for both reactions.
Potential Energy for the Transition State = -103.75 kcal/mol
Potential Energy for the H-H / F = -104.0kcal/mol
Potential Energy for the H-F / H = -133.7 kcal/mol
Therefore;
The activation energy for H + HF is +30.05 kcal/mol
The activation energy for F + H-H is +0.25 kcal/mol
In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy. How could this be confirmed experimentally?
The reaction F + H2 is exothermic. Due to the conservation of energy the amount of energy given out should be the same magnitude as the amount of energy taken in by the reverse reaction of H-F + H.
To confirm this experimentally, the reverse reaction of H-F + H should be carried out and the magnitude of the energy take in should be recorded then compared to the energy given out by the F + H2 reaction.
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state.
Based on the Hammond's postulate, the exothermic reactions have early transition states. With the higher translational energy, the reactants can rearrange themselves to form the transition state more easily. Hence, higher reaction efficiency is achieved when there is more translational energy compared to vibrational energy.