MRD:EP01189257
This report has been plagiarised.
EXERCISE 1: H + H2 system
Dynamics from the transition state region
On a potential energy surface diagram, how is the transition state mathematically defined?:
The transition state is defined as the maxima on the minimum energy path linking reactants and products, hence a stationary point on the potential energy surface. At the transition state, the derivative of the potential energy is zero with respect to each Cartesian coordinate.
and
However, a local minima on the potential energy surface corresponding to a well would have the same result. Therefore, to distinguish between a minima and the transition state the second derivative is determined, which can be calculated by finding the determinant of the Hessian matrix shown below.
The Hessian matrix of a convex function is positive semi-definite. Refining this property allows one to test if a critical point (x,y) is a local maximum, local minimum or saddle point.
If < 0 (exactly one negative eigenvalue), then (x,y) is an isolated local maximum.
If > 0 (exactly one positive eigenvalue), then (x,y) is an isolated local minimum.
If the Hessian has both positive and negative eigenvalues then (x,y) is a saddle point.
In other words, when
and if , we have a saddle point at (x0, y0) on a potential energy surface
How can the transition state be identified, and how can it be distinguished from a local minimum of the potential energy surface?:
The transition state is the maximum on the minimum energy path linking reactants and the products.
Local minimumː If one starts a trajectory exactly at a local minimum with no initial momentum, it will remain there forever. If one changes the geometry by a small amount, the system will revert back to its original state (local minimum) if the change is small enough.
Transition stateː Conversely, if one starts a trajectory exactly at the transition state, with no initial momentum, it will remain there forever. However, if one changes the geometry by an infinitesimal amount in the direction of the products it will roll towards the products (and similarly for the reactants).
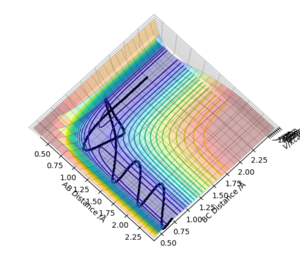
Report your best estimate of the transition state position (rts) and explain your reasoning illustrating it with a “Internuclear Distances vs Time” plot for a relevant trajectoryː
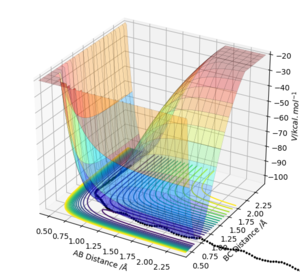
An initial estimate for the position of the transition state was made by observing the potential energy surface and was found to be 0.90 Å. At 0.90 Å, the internuclear distance against time plot showed that the internuclear distance was constantly oscillating. Therefore, the position of the transition state was further refined by increasing the number of decimal places until a horizontal line in the internuclear distance againt time plot was obtained.
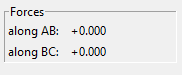
At rts = 0.907742 Å, the kinetic energy is 0. This means that HA and HBC are stationary, which is as predicted when the trajectory is started at the transition state with no initial momentum. Furthermore, the forces acting along AB and BC are 0 as should be the case in the transition state.
The internuclear distances (A-B, B-C and A-C) are constant over time, meaning that there is no change in geometry with respect to time, indicating a transition state position.
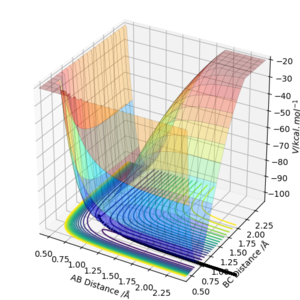
Comment on how the mep and the trajectory you just calculated differː
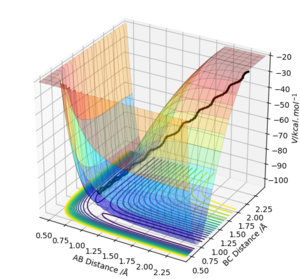
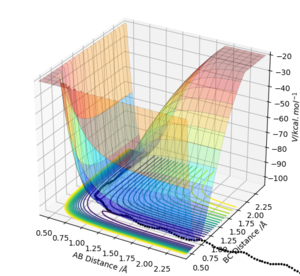
Both mep and the trajectory eventually resulted in H1+ H2-H3, where there is a steady increase in distance between H1 and H2.
MEP: Herein, the MEP method does not conserve total energy. There was no oscillation of the H2-H3 bond in mep and reaction path appears to be a relatively straight line indicating that the atoms are not vibrating (as shown below). The reactants change into the products in an infinitely slow motion, which is achieved by having the momenta/velocities reset to zero in each time step.
While the minimum energy path is useful in characterizing a chemical reaction, it does not provide a realistic representation of the motion of the atoms during the reaction. This is because the mass and inertia of the atoms have been ignored.
The trajectory: On the other hand, the reaction path is wavy indicating that the atoms are oscillating. Due to conservation of energy, kinetic energy and potential energy interchange, resulting in oscillation of the H2-H3 bond (as shown below).
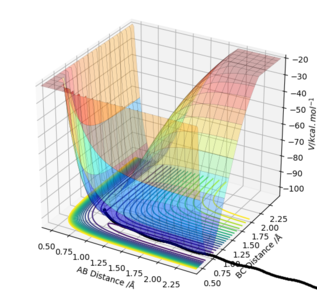
What would change if we used the initial conditions r1 = rts and r2 = rts + 0.01 instead?:
| At t = ∞ | r1 = rts + 0.01 and r2 = rts | r1 = rts and r2 = rts + 0.01 |
|---|---|---|
| r1/ Å | ∞ | oscillates at 0.73 |
| r2/ Å | oscillates at 0.73 | ∞ |
| p1/ kgÅs-1 | 2.5 | oscillates at 1.2 |
| p2/ kgÅs-1 | oscillates at 1.2 | 2.5 |
The system will end up with the formation of H1-H2 instead of H2-H3 bond (as shown below). For both mep and trajectory, values of r1 and r2 were swapped and so did p1 and p2. In summary, the reaction goes the opposite direction.
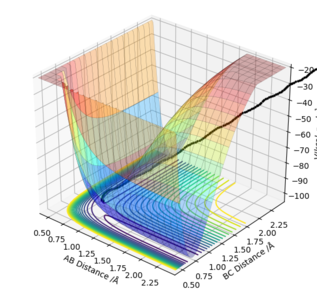
Setup a calculation where the initial positions correspond to the final positions of the trajectory you calculated above, the same final momenta values but with their signs reversed. What do you observe?:
By principle of microscopic reversibility,1 the opposite pathway occurs where the system returns back to the transition state. However, note that the system did not end up exactly at the transition state because the initial conditions (final conditions from previous calculations) used were not exact.
Reactive and unreactive trajectories
Complete the table above by adding the total energy, whether the trajectory is reactive or unreactive, and provide a plot of the trajectory and a small description for what happens along the trajectory. What can you conclude from the table?:
Reactants require enough kinetic energy to overcome the activation barrier to reaction. However, one must note that energy is not the only factor that can predict whether the trajectory is reactive. In the 2nd last example, despite its total energy being considerably higher than some of the other trajectories, it did not result in a reaction. Therefore, even if the atoms have sufficient kinetic energy to cross the activation energy barrier, barrier recrossing can occur if the atoms are too vibrationally excited, causing the trajectory to be unreactive.
State what are the main assumptions of Transition State Theory:
Main assumptions:1
- Electronic and nuclear motions are independent of each other (analogous to the Born-Oppenheimer approximation).
- The distribution of reactant molecules among the states correspond to the Boltzmann distribution.
- Once the molecular system crosses the transition state in the direction of products, it cannot turn around and reform reactants (fundamental assumption of TST).
- In the transition state, motion along the reaction coordinate may be decoupled from the other motions and regarded classically as a translation.
- Quasi-equilibrium between transition state and reactants
Given the results you have obtained, how will Transition State Theory (TST) predictions for reaction rate values compare with experimental values?:
The third assumption which forbids the 'recrossing' of the activation barrier and hence assumes that all reactants that reach the transition state will become product. However, based on the results obtained, it can be observed that not all trajectories that reach the transition state will result in a reaction because some may revert back to reactants, which Transition State Theory fails to take into account. A consequence of this is that TST overestimates the reaction values hence one would expect the experimental values to be lower.
For sake of completeness:
However, on the flipside, the TST breaks down for systems with light atoms such as hydrogens. In such systems, quantum effects become crucial. Quantum effects tend to increase the rate of the reaction for two reasons:
- particles lie in energy levels which are higher than the bottom of the potential energy well (there is additional zero-point energy).
- quantum tunneling through energy barrier
These two effects effectively lower the activation energy barrier. As a result, the rate of reaction predicted by TST could be less than what is obtained experimentally.
EXERCISE 2: F - H - H system
PES inspection
By inspecting the potential energy surfaces, classify the F + H2 and H + HF reactions according to their energetics (endothermic or exothermic):
F + H2 → HF + H: Exothermic
H + HF → H2 + F: Endothermic
How does this relate to the bond strength of the chemical species involved?:
The H-F bond (565 kJmol-1) is stronger than the H-H bond (432 kJmol-1) because of the polarization of charges in H and F resulting in stronger electrostatic attraction between them.2
Locate the approximate position of the transition stateː
Report the activation energy for both reactionsː
Using the same method as mentioned previously, the position of transition state and activation energy were found.
| Reaction | ratom/ Å
(distance between reactants) |
rdiatomic/ Å
(distance between atoms in diatomic molecule) |
Activation energy/ kcal mol-1 |
|---|---|---|---|
| F + H2 → HF + H | 1.8107 | 0.74488 | 0.258 |
| H + HF → H2 + F | 0.74488 | 1.8107 | 30.255 |
Reaction dynamics
Identify a set of initial conditions that results in a reactive trajectory for the F + H2, and look at the “Animation” and “Momenta vs Time”:
| rFH/ Å | rHH/ Å | pFH | pHH |
|---|---|---|---|
| 2.0 | 0.74 | 0 | -3 |
As seen from the figure below, the trajectory is reactive

In light of the fact that energy is conserved, discuss the mechanism of release of the reaction energy:


As seen from the two graphs above:
1. At the start of the reaction (t = 0 s):
- non-zero momentum for H-H (both translational and vibrational)
- zero momentum for F
- kinetic energy and potential fluctuate due to oscillation in H-H
2. At the transition state (t ~ 2.0 s): Two reactants meet at the transition state at before the momentum is redistributed to the two products (H and HF.
3. After the reaction:
- non-zero momentum for H (only translational)
- non-zero momentum for HF (both translational and vibrational)
- kinetic energy and potential fluctuate kinetic energy and potential fluctuate at larger amplitudes due to oscillation in H-F instead of H-H
In other words, translational and vibrational energy of H2 (reactant) has be released to vibrationally excite HF (product), resulting in:
- a vibrationally and translationally excited HF
- a translationally excited H
Explain how this could be confirmed experimentally:
Infrared spectroscopy can be used to obtain the IR spectrum of HF (IR-active 4460 cm-1).3 On the other hand H2 is not IR-active (no change in dipole moment) but is Raman active (change in polarizability) hence a Raman spectrum of H2 can be obtained. These spectra would shed light on the vibrationally excited states of HF and H2, and hence indicate transfer of vibrational energy from H2 to HF.
In addition, due to the heat released in this reaction, calorimetry could be used to monitor the progress of the reaction.
Discuss how the distribution of energy between different modes (translation and vibration) affect the efficiency of the reaction, and how this is influenced by the position of the transition state:
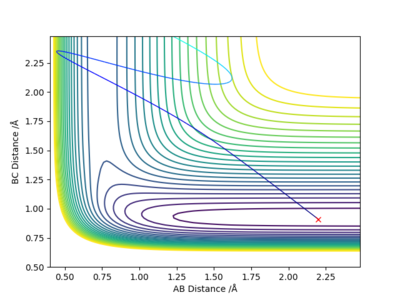
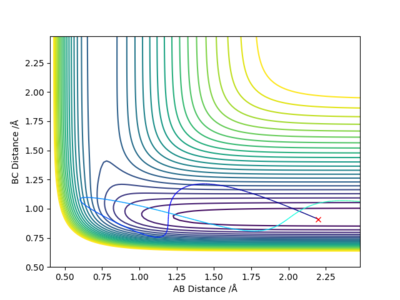
According to Polyani's rules, the location of the energy barrier (early/late transition state) heavily influences whether a certain initial distribution of reactant energy would lead to a reaction. It states that:4
- An early barrier (in an exothermic reaction) is most effectively crossed if reactants have high translational energy. On the other hand, high vibrational energy in the reactant may be ineffective for reaction.
- A late barrier (in an endothermic reaction) is most effectively crossed if reactants have high vibrational energy instead of the translational energy.
As F + H2 is an endothermic reaction with a late barrier, the first trajectory (with high vibrational and low translational energy) is reactive because, according to the Polyani's rules, the vibrationally excited molecules have the correct phase, which allows the system to surmount the barrier.
Conversely, the second trajectory (with low vibrational and high translational energy) is unreactive because the high translational energy of reactants results in the system simply 'slamming and bouncing off' the inner wall of the potential surface leading back into the reactant channel.
In conclusion, in order for a specific trajectory to be reactive, the vibrational energy of the reactants should be increased to promote an endothermic reaction with a late transition state while the translational energy of the reactants should be increased to promote an exothermic reaction with an early transition state.
References
1. Steinfeld, J. I., Francisco, J. S. & Hase, W. L. Chemical kinetics and dynamics. (Prentice Hall, 1999).
2. Libretexts. Bond Energies. Chemistry LibreTexts (2019). Available at: https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Chemical_Bonding/Fundamentals_of_Chemical_Bonding/Bond_Energies. (Accessed: 6th May 2019)
3. Hydrogen Fluoride, HF. Vibrational Modes of Hydrogen Fluoride Available at: http://www.chem.purdue.edu/gchelp/vibs/hf.html. (Accessed: 6th May 2019)
4. Hirst, D. M. (D. M. Potential energy surfaces: molecular structure and reaction dynamics. (Taylor & Francis, 1985)