MRD:01409469
Exercise 1: H + H2 system
Definition of a transition state
A potential energy profile results from plotting the potential versus reaction path.
The transition state is defined as the maximum on the minimum energy path linking reactants and products. This means that the transition state is a stationary point on the potential energy surface. Thus, at the transition state, the derivative of the potential energy is zero with respect to each Cartesian coordinate.
However, a local minimum on the potential energy surface corresponding to a well would have the same . Therefore, to distinguish between a local minimum on the potential energy surface and the transition state, the second derivative, is determined. This can be calculated by finding the determinant of the Hessian matrix shown below.
The Hessian matrix of a convex function is positive semi-definite. Refining this property allows one to test if a critical point (x,y) is a local maximum, local minimum or saddle point.[1]
If < 0 (exactly one negative eigenvalue), then (x,y) is an isolated local maximum.
If > 0 (exactly one positive eigenvalue), then (x,y) is an isolated local minimum.
If the Hessian has both positive and negative eigenvalues then (x,y) is a saddle point.
Excellent work, very well explained. Mys18 (talk) 16:58, 19 May 2019 (BST)
Locating the transition state

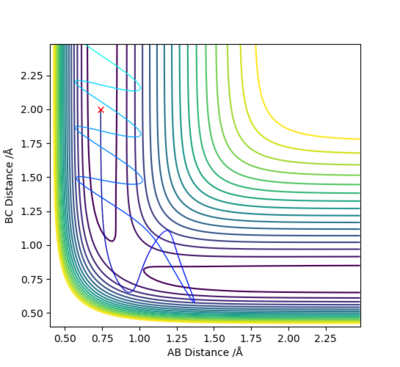
When the molecules are not at the transition state, a surface plot of the conditions shows a trajectory being plotted. This means that the trajectory is "rolling" towards the products or reactants. However, if a trajectory is started exactly at the transition state with no initial momentum, the molecules will remain at the transition state forever.
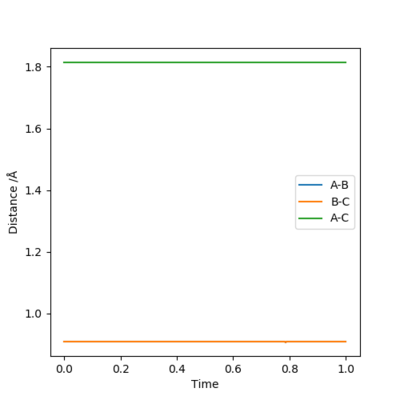
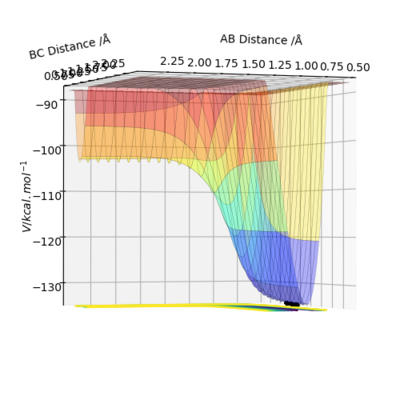
An initial estimate for the position of the transition state was made by observing the potential energy surface and was found to be 0.90 Å. At 0.90 Å, the internuclear distance against time plot showed that the internuclear distance was constantly oscillating. Therefore, the position of the transition state was further refined by increasing the number of decimal places until a horizontal line in the internuclear distance againt time plot was obtained. This means that the internuclear distance is constant and that the molecules are simply undergoing periodic symmetric vibration at the transition state. Therefore, the position of the transition state was determined to be 0.907743 Å.

When rAB=rBC=0.907743 Å and pA=pBC=0, the kinetic energy is 0. This means that HA and HBC are stationary, which is as predicted when the trajectory is started at the transition state with no initial momentum. Furthermore, the forces acting on HA and HBC are 0 as should be the case in the transition state.
Great explanation of your methodology. Mys18 (talk) 17:04, 19 May 2019 (BST)
Calculation type: Dynamic and minimum energy path
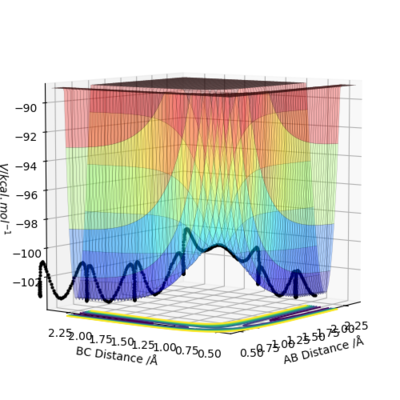
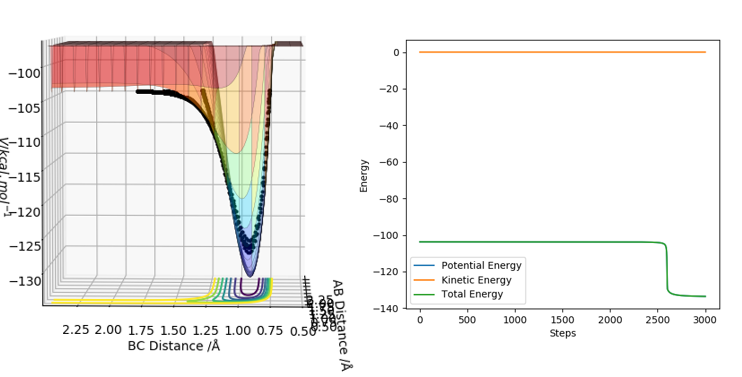
The minimum energy path, is the lowest energy path from the reactants to the products. The minimum energy path is determined by following the mode corresponding to the negative Hessian eigenvalue in both directions along the steepest descent direction.[1] Following this path allows one to approach two valleys of stable structures. The resulting path generated is the minimum energy path. The reaction paths were chartered for a dynamic and a minimum energy path. The initial conditions used were that of the transition state except that the internuclear distance between HA and HB had increased to 0.917743 Å. The reaction path obtained using the two different calculation methods was different.
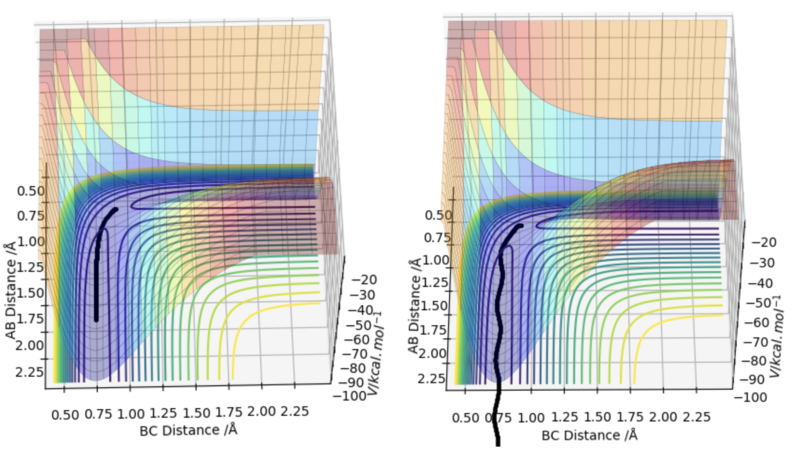
On the surface plot, the reaction path is depicted by the black line. Following the minimum energy path, the trajectory simply follows the valley floor to Ha+Hb-Hc. The reaction path appears to be a relatively straight line indicating that the atoms are not vibrating. In the minimum energy path, the reactants change into the products in an infinitely slow motion. This is done by having the momenta/velocities reset to zero in each time step. While the minimum energy path is useful in characterising a chemical reaction, it does not provide a realistic representation of the motion of the atoms during the reaction. This is because the mass and inertia of the atoms have been ignored.
Since the atoms simply follow the minimum energy path, they do not undergo slight displacements into surrounding valleys of higher potential energy. Furthermore, because the atoms are assumed to have no inertia, they do not undergo vibrations even if they were to be displaced to valleys of higher potential energy.
However, when dynamic calculation is performed, the reaction path is wavy indicating that the atoms are oscillating. This is because the atoms are displaced to regions of higher potential on the path from reactants to products. This leads to atom oscillation due to the inertia of the atoms.
Exactly! The MEP method does not conserve the total energy (straight line) whereas with the dynamic method it does (oscillating line). Mys18 (talk) 17:08, 19 May 2019 (BST)
Internuclear distance against time plot
Setting the initial system conditions such that rAB= 0.907743, rBC= 0.917743 and pA= pBC= 0:

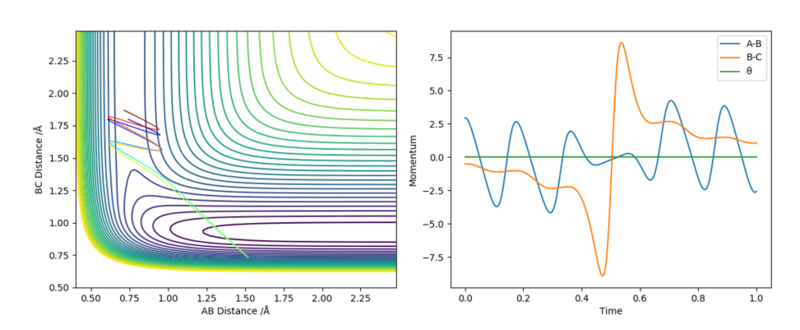
In the minimum energy path, the distance between HA and HB decreases from 0.90 Å to approximately 0.79 Å during the first 50 steps before plateauing off to a value of 0.74 Å which is the approximate length of a hydrogen bond. This means that a bond was formed between HA and HB. In addition, the plateau indicates that the bond is static. On the other hand, the distance between HB and HC has increased to 1.91 Å at large step values. This shows that HC has been ejected off following a successful collision between HA and HBC.
Similarly, in the dynamic trajectory, the distance between HA and HB decreases to approximately 0.75 Å after 0.3 s. This is indicative of hydrogen bond formation between HA and HB. In addition, the distance between HB and HC increases to 3.44 Å after HC is ejected following a successful collision.
One obvious difference between the two plots is that in the minimum energy path trajectory, the internuclear distance between HA and HB is constant indicating that the bond is static. However, in the dynamic trajectory the internuclear distance is oscillating showing the the bond is vibrating. This difference could be attributed to the fact that minimum energy path does not take oscillatory motion of atoms into account while dynamic trajectory does.
However, changing the initial conditions of the system such that rAB = 0.917743 Å, rBC = 0.907743 Å and pA=pBC=0:

In this case, a hydrogen bond of length 0.77-0.79 Å is formed between HB and HC while HA is repelled away to beyond 3.45 Å.
Additionally, from the internuclear distance plot it can be seen that the distance between HB and HC increases in a rectangular hyperbola fashion when calculated using the minimum energy path. On the other hand, the internuclear distance between HB and HC increases in a linear manner when dynamic calculation is applied. A possible reason for this difference is that in the minimum energy path, the atoms are not vibrating and as such reach the maximum distance and plateau at a faster rate. However, in the dynamic calculation, the atoms have momentum and as such move further away from each other.
Reactive and unreactive trajectories
With the initial positions r1 = 0.74 and r2 = 2.0, trajectories were run with the momenta combination shown below.
From the table, it can be seen that the chance of a reaction successfully occurring is not solely dependent on the amount of kinetic energy the atoms possess. Even if the atoms have sufficient kinetic energy to cross the activation energy barrier, barrier recrossing can occur if the atoms are too vibrationally excited.
Fantastic job on this section! Exactly, your conclusion is spot on and perfectly supported by REACTION 4. Mys18 (talk) 17:26, 19 May 2019 (BST)
Transition State Theory
Transition state theory provided the first theoretical attempt to determine absolute reaction rates. In this theory, a transition state separating the reactants from products is used to find an expression for the thermal rate constant.
The main assumptions of transition state theory are[2]:
1. Electronic and nuclear motions are separated (equivalent to the Born-Oppenheimer approximation in quantum mechanics)
2. Reactant molecules are distributed among their states in accordance with the Maxwell-Boltzmann distribution
3. Molecular systems that have crossed the transition state in the direction of products cannot turn around and reform reactants
4. In the transition state, motion along the reaction coordinate may be separated from the other motions and treated classically as a translation
5. Even in the absence of an equilibrium between reactant and product molecules, the transition states that are becoming products are distributed among their states according to the Maxwell-Boltzmann laws
The goal of transition state theory is to predict the rate constant, k, of a reaction given a potential energy surface for the reaction.
However, transition state theory suffers from a set of limitations due to the assumptions stated above not holding true in reality.[3]
Firstly, transition state theory assumes that barrier recrossing is negligible. However, as seen from the fourth trajectory in table 1, barrier recrossing occurred because the atoms were too vibrationally excited and the system reverted back to the reactants even though the system had already crossed the transition state region. In this situation, transition state theory would predict a faster rate of reaction compared to what was obtained experimentally.
Secondly, the transition state theory breaks down for systems with light atoms such as hydrogens. In such systems, quantum effects become crucial. Quantum effects tend to increase the rate of the reaction for two reasons. First, particles lie in energy levels which are higher than the bottom of the potential energy well (there is additional zero-point energy). Secondly, the particles can tunnel through the barrier. These two effects effectively lower the activation energy barrier. As a result, the rate of reaction predicted by transition state theory would be less than what is obtained experimentally.
Lastly, transition state theory does not hold true for systems which are far from equilibrium. In such cases, the assumption of a starting Boltzmann distribution breaks down.
Good, nice to see you have understood these assumptions and explained when TST does fail! Mys18 (talk) 17:35, 19 May 2019 (BST)
Exercise 2: F - H - H system
Potential energy surface inspection
F + HA-HB → HA-F + HB

The reaction between F and H2 is an exothermic reaction. This means that the reactants are at a higher energy than the products. The overall reaction involves the breaking of a hydrogen bond and the formation of a hydrogen-fluorine bond. The HF bond formed is stronger than the hydrogen bond that was broken. This is because fluorine is more electronegative than hydrogen resulting in a polar HF bond. The negative enthalpy of H-F bond formation is greater than the positive enthalpy of hydrogen bond dissociation. Therefore, the reaction between F and H2 is an exothermic reaction.
HA + HB-F → HA-HB + F
The reaction between H and HF is an endothermic reaction. The products are at a higher energy level than the reactants. The overall reaction involves the breaking of a HF bond and the formation of a hydrogen bond. The formation of a homonuclear H2 molecule results in a non-polar hydrogen bond being formed. The HF bond broken is stronger than the hydrogen bond that was formed. The negative enthalpy of hydrogen bond formation is less than the positive enthalpy of hydrogen-fluorine dissociation. Therefore, the reaction between H and HF is endothermic.
Correct, good use of your own knowledge with bonding to back up why H-F bond is stronger. Mys18 (talk) 17:42, 19 May 2019 (BST)
Locating the transition state
A = HA, B = HB, C = F:
As mentioned previously, when the molecules are not at the transition state, a reaction path will be plotted. However, if the initial conditions of the system are set such that the trajectory is started exactly at the transition state with no initial momentum, the molecules will remain at the transition state forever.
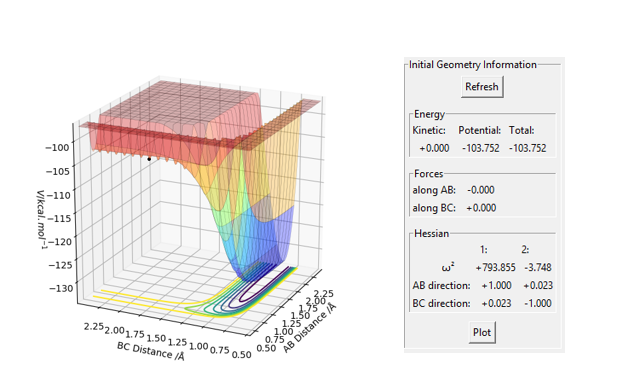
An initial estimate for the transition state was made by setting rAB = 0.74 which is the length of a hydrogen bond. The position of the transition state was further refined by increasing the number of decimal places such that the final value of rAB was found to be 0.74478 and rBC = 1.81079. This set of distances gave a reaction path that was represented by a point indicating that no trajectory was plotted and that the molecules remained at the transition state since their initial momentum was 0.
Moreover, the kinetic energy as well as the forces acting on the atoms was calculated to be 0, which is consistent with the transition state.
Therefore, the position of the transition state was found to be at rAB = 0.74478 and rBC = 1.81079 when pA = pBC = 0.
Good, don't forget units, what should these be? Mys18 (talk) 17:46, 19 May 2019 (BST)
Determining the activation energy
By reducing the value of rBC by 0.01, the atoms are no longer at the transition state and would move towards the formation of products. The activation energy was found by calculating the change in total energy after the reaction. The activation energy of F + H2 → HF + H was found to be +23.279 kcal/ mol.

The activation energy of FH + H → F + H2 was found by calculating the small dip in potential energy. The activation energy was found to be +0.280 kcal/ mol.
Excellent! Mys18 (talk) 17:48, 19 May 2019 (BST)
Reaction dynamics of F + HA-HB → HA-F + HB
The set of initial conditions that result in a reactive trajectory for F + H2 is as follows: rHH = 0.74 Å, rHF = 1.79 Å and pHH = pHF = 0.

Initially, the H2 molecule is travelling in a relatively straight line with very little oscillations as evidenced by the low amplitude of momentum between 0-2 s. Following successful collision between F and H2, the amplitude of momentum of the product, HF, increases dramatically. This is because the reaction between F and H2 is exothermic and the excess energy released causes the molecule to become vibrationally excited and the amplitude of oscillations in the product to increase in the form of H-F vibrations.

The law of conservation of energy states that energy cannot be created or destroyed. It simply changes from one form to another. As can be seen from the graph in figure 16, total energy remains constant. In this reaction, potential energy is converted to kinetic energy. A decrease in potential energy of the atoms following a successful collision between F and H2 results in an equal increase in kinetic energy which manifests in the form of increased product (HF) oscillations.
This can be confirmed experimentally using infrared chemiluminescence.[2] Observation of radiation from excited product molecules is a clear indication that these molecules are produced in the excited state. If the excitation is primarily vibrational, the radiation will appear in the infrared region of the spectrum (between 3-15 μm). This technique has been used extensively in hydrogen halogen reactions which produce HX molecules in the excited state.
One such experiment involves the use of the arrested relaxation method.[2] In this technique, the reaction is carried out in a chamber whose walls are maintained at a very low temperature (20 K). This results in cryopumping of the chamber in that all the products and unreacted starting materials are condensed on the walls and only those product molecules that radiate before being pumped away are observed.
Great identification of the link between the heat from the reaction and vibration of the molecule. Fantastic knowledge, I have learnt from your answer, thanks for the reference I will check out the final method! Mys18 (talk) 17:53, 19 May 2019 (BST)
Polanyi's empirical rules
In a typical chemical reaction, there is an energetic barrier — a saddle point that the reactants must surmount to become products. Which form of energy is initially deposited in the reactants, translational or vibrational, is more efficacious in surmounting the activation energy barrier is one of the core topics in the area of reaction dynamics. The Polyani rules state that vibrational energy is more effective at promoting a late-barrier reaction (transition state resembles products). Conversely, translational energy is better at promoting an early-barrier reaction (transition state resembles the reactants).[4]
The forward reaction between H2 and F is exothermic. Therefore, the transition state is closer to the reactants than to the products in energy. Since the transition state occurs early in an exothermic reaction, translational energy is more effective at promoting an exothermic reaction than vibrational energy.
Conversely, the backward reaction between H and HF is endothermic. According to Hammond's postulate, the transition state resembles the products more than it resembles the reactants. Therefore, in an endothermic reaction, a late transition state is observed and vibrational energy is more effective at promoting a reaction than translational energy.
Good. Mys18 (talk) 17:54, 19 May 2019 (BST)
Promoting the forward reaction: F + HA-HB → HA-F + HB
1. The initial system conditions used are: rHH = 0.74 Å, rHF = 1.8 Å, pHH = 2.95 and pHF = -0.5.
Vibrational energy is represented by pHH while translational energy is represented by pHF.
A molecule of H2 collides with F. However, the collision is unsuccessful and no reaction occurs. A reaction did not occur even though the molecules have sufficient kinetic energy to overcome the activation energy barrier. This is because most of the energy is deposited in the reactants as H-H vibrations as seen by the large oscillations in H2. Barrier recrossing has occured as a result of the large vibrational energy causing the system to revert back to the reactants even though the system has already crossed the transition state and a bond was formed between HB and F temporarily.
This appears to run counter to what one would expect to happen when more energy is put into the system. It is predicted that when more energy is put into the system, the reactants would possess more kinetic energy to overcome the activation energy barrier. However, as can be seen from the simulation above, an increase in the vibrational energy of the reactants is not effective at promoting the occurrence of an exothermic reaction with an early transition state. This is in accordance to Polyani's rules.
2. The initial system conditions used are: rHH = 0.74 Å, rHF = 1.8 Å, pHH = 0.1 and pHF = -0.8.
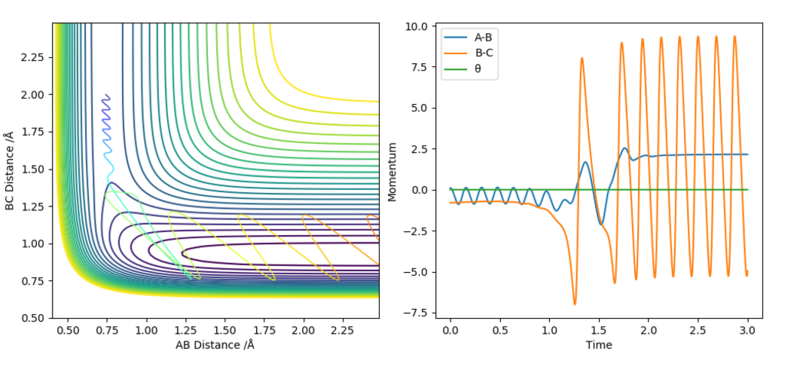
The collision between a molecule of H2 and F is successful and a chemical reaction has occurred. A reaction has occurred even though the overall energy of the system has been significantly reduced by lowering the amount of vibrational energy in the reactants but slightly increasing the amount of translational energy deposited in the reactants. Therefore, H2 and F have more translational energy to move towards each other and form a H-F bond. The product formed is vibrationally excited as seen by the large amplitude of oscillations in the product HF which correspond to the strong H-F vibrations.
From the second simulation, it can be seen that an increase in translational energy in the reactants is more effective at promoting an exothermic reaction with an early transition state to occur, which again follows Polyani's rules.
Good, nice set of results to support Polanyi's rules. Mys18 (talk) 17:59, 19 May 2019 (BST)
Promoting the backward reaction: HA + HB-F → HA-HB + F
1. The initial system conditions used are: rFH = 0.92 Å, rHH = 2.0 Å, pFH = 0.2 and pHH = -3.0.
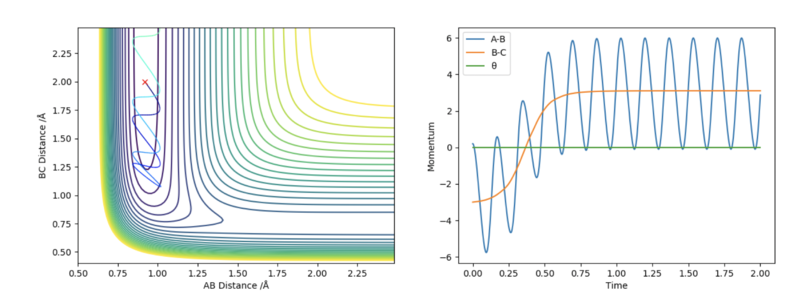
An atom of HA collides with a molecule of HBF. However, the collision is unsuccessful and no chemical reaction occurs. This is because the reactants lack sufficient vibrational energy to surmount the activation energy barrier. Therefore, following an unsuccessful collision with HBF, HA simply bounces off and moves away at constant momentum. This is in agreement with Polyani's rules which state that vibrational energy is more effective than translational energy at promoting reactions with a late transition state, for example, endothermic chemical reactions.
2. The initial system conditions used are: rFH = 0.92 Å, rHH = 2.0 Å, pFH = 7.1 and pHH = -0.5.

Increasing the amount of vibrational energy in the reactants by increasing pFH resulted in a chemical reaction successfully occurring. This is because the reactants now have sufficient kinetic energy in the form of H-F vibrations to overcome the activation energy barrier. In addition, because the reaction between HA + HB-F is endothermic, energy is taken in from the surroundings during the reaction and the products are less vibrationally excited than the reactants. This can be seen in the lower amplitude of oscillations in the product formed.
In conclusion, the vibrational energy of the reactants should be increased to promote an endothermic reaction with a late transition state while the translational energy of the reactants should be increased to promote an exothermic reaction with an early transition state. All 4 simulations shown above obey Polyani's rules.
This has been an exemplary report. All answers were well explained hitting all nails on the head. Very good understanding and utilising your knowledge of techniques for Q8. Well done :) Mys18 (talk) 18:05, 19 May 2019 (BST)
References
- ↑ 1.0 1.1 A. C. Vaucher, M. Reiher, J. Chem. Theory. Comput., 2018, 14, 3091-3099.
- ↑ 2.0 2.1 2.2 J. I. Steinfield, J. S. Francisco, W. L. Hase, Chemical Kinetics and Dynamics, Pearson, 1998.
- ↑ D. C. Elton, Transition State Theory for Physicists, 2013.
- ↑ Z. Zhang, Y. Zhou, D. H. Zhang, J. Phys. Chem. Lett., 2012, 3, 3416-3419.