Introduction

In this part we are going to explain the interest and the theory of ONIOM calculations.

Principles

The ONIOM method (Our own N-layered Integrated molecular Orbital and molecular Mechanics) was developed by Morokuma and co-workers in 1996.

First, ONIOM's method is associated to hybrid methods, which rely on the concept that some reactions occur in a localized region of the molecule, where the remainder of the system plays a more minor, sometimes purely structural role. However, inclusion of the surroundings is important since it can affect reactivity and reaction pathways.

Thus, ONIOM is a method that allows different regions of a chemical system to be defined, which are each treated with a different level of theory. The chemical process being investigated can therefore be treated at an appropriate high-accuracy computational level, while the remainder of the system (the “spectator” or low-level region) can be treated only with a lower level of theory. In this way, no computational time is “wasted” on parts of the system that do not need it.

The energy of the molecule ( = $E^{O N I O M}$ ) is obtained through an extrapolation:

$E^{O N I O M} = E_{m o d e l}^{h i g h} + E_{r e a l}^{l o w} - E_{m o d e l}^{l o w}$

Figure 1

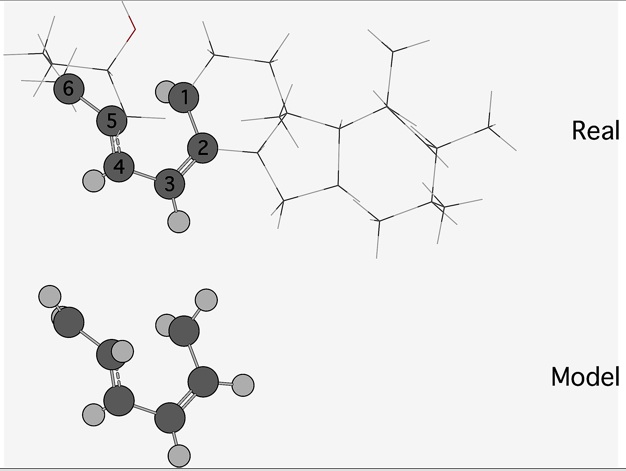
The model is a (sub)system based on a small fragment of the full real system/molecule, as shown for previtamin D "in Figure1". Here, the chemical process being studied - electronic excitation - will be localized in the model system. The high level method is the more accurate quantum mechanical (QM) level of theory (CASSCF,...), whereas the low-level method can be cheaper (e.g., HF, AM1, or UFF). ONIOM is an attempt to reproduce a calculation at the high level of theory for the real system, a calculation we define as the Target (and which we generally want to avoid carrying out, because of the computational cost). The absolute energy $E_{}^{O N I O M}$ differs (unless the high and low levels of theory are the same) from the absolute Target energy $E_{r e a l}^{h i g h}$ . However, energy differences between two points on a potential energy surface (or between two potential energy surfaces at a particular geometry) will be reproduced

$Δ E^{T a r g e t} = Δ E_{r e a l}^{h i g h} \approx Δ E^{O N I O M}$

provided that the effects of changing partition size between regions, given by

$E_{r e a l}^{l o w} - E_{m o d e l}^{l o w}$

and level of theory, given by

$E_{r e a l}^{h i g h} - E_{m o d e l}^{l o w}$

are separable.

The ONIOM method adds the substituent effect to the high-level model calculation, saving computational time and resources by limiting (expensive and slow) accurate calculations to a small molecule fragment where they are essential. The surroundings can be described by much cheaper and faster computational methods, which may give poor results on their own, yet have a beneficial effect on the model fragment calculation.

ONIOM is a general hybrid method, since the low-level method can be either QM or molecular mechanics (MM). Any computational method can be used in ONIOM without modification, and in most cases, properties that can be obtained with the individual methods can also be obtained when those methods are combined in ONIOM.

Different levels of theory

Two-layer system

The ONIOM energy for a two-layer system (two levels of theory) is written in the form of an extrapolation:

$E^{O N I O M} = E_{m o d e l}^{h i g h} + E_{r e a l}^{l o w} - E_{m o d e l}^{l o w}$

The real system contains all of the atoms, from both the high-level and low-level regions; the model system contains only the atoms that belong to the high-level region and the link hydrogen atoms that are used to saturate the dangling bonds that result from covalent interactions between the regions (show in Figure 1).
The real system is only calculated with the low-level method, whereas the model system is calculated with both the high- and low-level methods. So, it is important to realize that the terms

$E_{r e a l}^{l o w} - E_{m o d e l}^{l o w}$

describe both the contribution from the low-level region (the region treated only at the low level of theory) as well as the interaction between the high-level and low-level regions.
In other words, the coupling between the two regions is always evaluated at the low computational level of theory.

Because all the terms ( $E^{O N I O M}, E_{m o d e l}^{h i g h}, E_{r e a l}^{l o w}, E_{m o d e l}^{l o w}$ ) involve chemically realistic systems, ONIOM can be used to combine QM with QM methods, as well as QM with MM methods. The positions of the necessary link atoms are defined in terms of the positions of the corresponding atoms in the real system.
The potential energy surface is therefore well defined, and any conventional method for the investigation of potential surfaces (e.g., gradientdriven optimization, IRC,...) can be used with ONIOM as well.

Multi-layer ONIOM calculations

This equation :

$E^{O N I O M} = E_{m o d e l}^{h i g h} + E_{r e a l}^{l o w} - E_{m o d e l}^{l o w}$

can be generalized for any number of layers (for example, in the three layer case, an INTERMEDIATE layer is also selected, which is an extension of the MODEL region), where each additional layer introduces two additional energy calculations, but in this tutorial, we are only developped the two-layer ONIOM calculations.

Furthermore, this method is a potentially N-layered hybrid calculation meaning that the system could be divided into N layers, but is currently only implemented for two and three layers in the Gaussian package.

Problem of link atoms

A subtle point that can be missed when setting up a job in GaussView is how the bonds are terminated in the MODEL region. Separation of the regions involves cutting of covalent bonds and these 'dangling bonds' are capped using Link Atoms. The Link Atoms can be any specified atom, for instance a CF3 group can be replaced by a fluoride atom. In practice, however, hydrogen atoms have been found to be the best Link Atoms, irrespective of the groups they replace. In GaussView this is the default, although it can be easily changed by the user.

The Link Atom is added along the same vector of the original atom and is scaled according to a predetermined scale factor, g, for each pair of atoms, i.e. the original atom and the Link Atom.
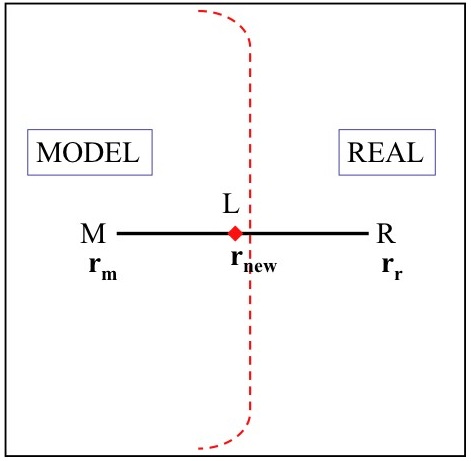
To illustrate this point, if we look at the bond distance between a MODEL atom M, with position vector, $r_{m}$ , connected to an atom belonging to the REAL system, with position vector, $r_{r}$ , the bond vector between them is defined as $r_{m} - r_{r}$ which is shown in the following diagram.

If a Link hydrogen atom, L, is placed along the bond vector between the atoms R and M, the position vector, $r_{n e w}$ , is calculated according to the formula:

$r_{n e w}^{} = r_{m} + g (r_{r} - r_{m})$

Optimization : ONIOM gradient

The ONIOM gradient can be written as :

$g^{O N I O M} = \frac{\partial E^{O N I O M}}{\partial q} = \frac{\partial E_{r e a l}^{l o w}}{\partial q} + \frac{\partial E_{m o d e l}^{h i g h}}{\partial q^{m}} J - \frac{\partial E_{m o d e l}^{l o w}}{\partial q^{m}} J = \frac{\partial E_{r e a l}^{l o w}}{\partial q} + \frac{\partial E_{m o d e l}^{h i g h}}{\partial q} - \frac{\partial E_{m o d e l}^{l o w}}{\partial q}$

The Jacobian J is related to the internal coordinates ( $q_{}^{}$ ), so it converts the coordinate system for the model system, $q_{}^{m}$ , to the coordinate system for the real system, $q_{}^{}$ .

So, during an optimization, as usual, Gaussian tries to tend the gradient to zero. But in the ONIOM case, $g_{}^{O N I O M}$ tends to zero and so the different components of $g_{}^{O N I O M}$ do not tend to zero. To check that the calculation has not found large individual components which are equal and opposite in sign, determine the second derivatives for each region via a force constant calculation.

Tutorials

Run an ONIOM calculation on a simple system.

First steps with ONIOM

Next part ONIOM for excited states

Back to ONIOM