Frequencies calculations
Calculations
In Calculate --> Gaussian --> Job style, choose Frequency. Then select your Method, enter the Title, Edit and save with the appropriate name.
What can you find on the file .log ?
In this file you can get all the previous information concerning the position of the atom in the space or the Mulliken atomic charges, or over the energy of the molecule. Below I am just going to talk about the specific informations that we can get from these calculations.
Frequencies and intensities
The main result that we get is obviously concerning the frequencies. The calculation run by Gaussian predicts the frequencies and intensities for each spectral line.
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman scattering
activities (A**4/AMU), depolarization ratios for plane and unpolarized
incident light, reduced masses (AMU), force constants (mDyne/A),
and normal coordinates:
1 2 3
A" A" A'
Frequencies -- 846.4293 846.5877 918.7981
Red. masses -- 1.0227 1.0222 3.5971
Frc consts -- 0.4317 0.4317 1.7891
IR Inten -- 0.0000 0.0000 20.0503
Atom AN X Y Z X Y Z X Y Z
1 6 0.00 0.00 -0.03 0.00 0.00 0.00 -0.08 0.28 0.00
2 6 0.00 0.00 0.01 0.00 0.00 -0.03 -0.18 -0.20 0.00
3 6 0.00 0.00 0.02 0.00 0.00 0.02 0.28 -0.04 0.00
4 1 0.07 -0.31 0.19 0.44 0.05 -0.03 -0.14 0.24 0.03
5 1 -0.07 0.31 0.19 -0.44 -0.05 -0.03 -0.14 0.24 -0.03
6 1 0.31 0.30 -0.07 -0.17 0.29 0.17 -0.26 -0.34 -0.01
7 1 -0.31 -0.30 -0.07 0.17 -0.29 0.17 -0.26 -0.34 0.01
8 1 0.34 -0.21 -0.12 0.07 0.36 -0.15 0.31 -0.15 0.02
9 1 -0.34 0.21 -0.12 -0.07 -0.36 -0.15 0.31 -0.15 -0.02
4 5 6
A' A" A'
Frequencies -- 918.9332 951.2503 1176.0223
Red. masses -- 3.6014 1.0478 1.2778
Frc consts -- 1.7918 0.5586 1.0412
IR Inten -- 20.0174 0.9866 13.2726
Atom AN X Y Z X Y Z X Y Z
1 6 0.25 0.09 0.00 0.00 0.00 0.03 0.13 0.00 0.00
2 6 -0.22 0.19 0.00 0.00 0.00 0.03 0.01 0.06 0.00
3 6 -0.07 -0.27 0.00 0.00 0.00 0.03 0.01 -0.06 0.00
4 1 0.41 0.08 0.01 0.00 0.35 -0.21 -0.58 0.00 0.00
5 1 0.41 0.08 -0.01 0.00 -0.35 -0.21 -0.58 0.00 0.00
6 1 -0.17 0.20 -0.03 0.31 -0.17 -0.21 -0.14 -0.24 -0.02
7 1 -0.17 0.20 0.03 -0.31 0.17 -0.21 -0.14 -0.24 0.02
8 1 0.02 -0.37 -0.02 0.31 0.17 -0.21 -0.13 0.23 -0.02
9 1 0.02 -0.37 0.02 -0.31 -0.17 -0.21 -0.13 0.23 0.02
Thermochemistry
Because all frequency calculations require thermochemical analysis of the system, you get these informations too, and they begin in this part (Cyclopropane, DFT, 6-21G) :
------------------- - Thermochemistry - ------------------- Temperature 298.150 Kelvin. Pressure 1.00000 Atm. Atom 1 has atomic number 6 and mass 12.00000 Atom 2 has atomic number 6 and mass 12.00000 Atom 3 has atomic number 6 and mass 12.00000 Atom 4 has atomic number 1 and mass 1.00783 Atom 5 has atomic number 1 and mass 1.00783 Atom 6 has atomic number 1 and mass 1.00783 Atom 7 has atomic number 1 and mass 1.00783 Atom 8 has atomic number 1 and mass 1.00783 Atom 9 has atomic number 1 and mass 1.00783 Molecular mass: 42.04695 amu.
You can check that you obtain informations concerning Temperature, Pressure and Isotopes.
Then you have the prediction of important quantities in thermodynamic chemistry like the different contribution of the energy :
E (Thermal) CV S
KCal/Mol Cal/Mol-Kelvin Cal/Mol-Kelvin
Total 53.335 10.009 59.833
Electronic 0.000 0.000 0.000
Translational 0.889 2.981 37.136
Rotational 0.889 2.981 21.688
Vibrational 51.558 4.048 1.009
Normal mode
The output of the calculation frequency displays the normal modes too. Thus, by reading the output, you can know from the standart orientation which will be the displacements of the nuclei on the first normal mode and the next.
Below is the standart orientation of the propene (HF 6-21G)
Standard orientation:
---------------------------------------------------------------------
Center Atomic Atomic Coordinates (Angstroms)
Number Number Type X Y Z
---------------------------------------------------------------------
1 6 0 -1.267758 -0.250018 0.000000
2 1 0 -1.198196 -1.317754 0.000000
3 1 0 -2.228162 0.221706 0.000000
4 6 0 -0.143644 0.506907 0.000000
5 1 0 -0.213207 1.574644 0.000000
6 6 0 1.238620 -0.172023 0.000000
7 1 0 1.336374 -0.782018 -0.873642
8 1 0 2.003500 0.576214 -0.000019
9 1 0 1.336389 -0.781988 0.873661
---------------------------------------------------------------------
So by reading of the table you can conclude that 6 atoms do not have component on the Z axe.
And below there are the normal modes corresponding to the 3 first spectral lines.
1 2 3
A A A
Frequencies -- -335.1037 464.3695 635.5071
Red. masses -- 1.0876 1.9437 1.2391
Frc consts -- 0.0720 0.2469 0.2948
IR Inten -- 0.4657 0.2197 19.8327
Raman Activ -- 3.1749 3.0871 16.1833
Depolar (P) -- 0.7500 0.4940 0.7500
Depolar (U) -- 0.8571 0.6613 0.8571
Atom AN X Y Z X Y Z X Y Z
1 6 0.00 0.00 0.06 -0.16 0.05 0.00 0.00 0.00 0.04
2 1 0.00 0.00 0.27 -0.55 0.03 0.00 0.00 0.00 -0.40
3 1 0.00 0.00 -0.03 0.01 0.41 0.00 0.00 0.00 0.68
4 6 0.00 0.00 -0.06 0.01 -0.18 0.00 0.00 0.00 -0.14
5 1 0.00 0.00 -0.29 0.05 -0.18 0.00 0.00 0.00 0.35
6 6 0.00 0.00 0.01 0.14 0.06 0.00 0.00 0.00 0.01
7 1 0.24 0.39 -0.24 0.36 0.11 -0.01 0.26 -0.10 0.12
8 1 0.00 0.00 0.54 -0.12 0.33 0.00 0.00 0.00 0.21
9 1 -0.24 -0.39 -0.24 0.36 0.11 0.01 -0.26 0.10 0.12
So for example you learn that for the frequency of 464.3695 the first atom move of -0.16 on the X axe and 0.05 on the Y axe.
Imaginary frequency
What does it correspond to ?
When you occur a reaction you have at the beginning a reactant, at the end a product and to obtain this product you have to pass a barrier which correspond to a certain energy. At the top of this barrier we are in a transition state. This transition state is most of the time unstable, you can not observe it. The imaginary frequency corresponds to the frequency that bring you on the top of this barrier.
Very often we use the frequencies calculations after an optimization to determine the nature of the stationary point found with the geometry optimization. Because a successful optimization of geometry may bring a structure which is a minimum structure or a saddle point. A saddle point is like a minimum but just in such directions of the surface and a maximum in the other directions. The first order saddle points correspond to the transition state (which we can define as a maximum between two minima).
What are the differents situations ?
If you were looking for a minimum.
| Imaginary frequencies ? | What does it mean ? | What do you have to do next ? |
| No imaginary frequencies | Your structure is a minimum | You got what you want, continue to work with this structure |
| 1 or more imaginary frequencies | Your structure is a saddle point (not a minimum!!) | Modify the geometry of your molecule, optimize again and run an other frequencies calculation. |
If you were looking for a transition state.
| Imaginary frequencies ? | What does it mean ? | What do you have to do next ? |
| No imaginary frequencies | Your structure is a minimum, not a transition state. | Try to optimize your structure with TS Berny. |
| 1 imaginary frequency | Your structure is a true transition state. | You obtained what you would like so continue to work with this struture. |
| More than 1 imaginary frequency | Your structure is a higher order saddle point, so it is a transition state but which connects 2 minima. | Modify the geometry of your molecule, run again the optimization with the TS Berny parameters, or try with QST2,QST3.. |
Advice Break
If you want to use QST2 or QST3, have a look at Appendix 1 : TS Berny, QST2 or QST3 ??
Characterizing stationary points
So we spoke about imaginary frequencies but I never explain how we see that we have an imaginary frequency!
In the part of the file .log where there is the details of all the frequencies you have to find a negativ frequency and this would be your imaginary frequency! If your eyes are so tired that they can not search in the file, have a look at the Advice Break.
Advice break
To known very quickly if you have an imaginary frequency in your file type on the Terminal the command grep imagin nameofthefile.log and it will do for you! But if you have one (or many!) imaginary frequency you have always to look at the figures in the table...or maybe not (look at Animated frequencies)
Optimization + frequencies calculations
I wrote that one of the most use of the frequencies calculation is to run this after the optimization of your structure. But instead of running the two separately you can do the two in the same time you just have to take Job style --> Opt+Freq, ask for an optimization in a minimum or in a transition state (TS Berny).
Thus you file .log will include all the informations concerning the optimization and the frequencies.
Animated frequencies
The results of the frequencies calculation can be see in animation. Open you file .log with Gaussview, and then click on Results --> Vibrations. A third window have to open with your molecule and a table with all the frequencies (it is easier to look at which of them have negativ sign). And by clicking on Start you can visualize the displacement of the atom for each frequency. You can click on Show Displacements Vectors which is very helpful to have a good visualization of the displacement.
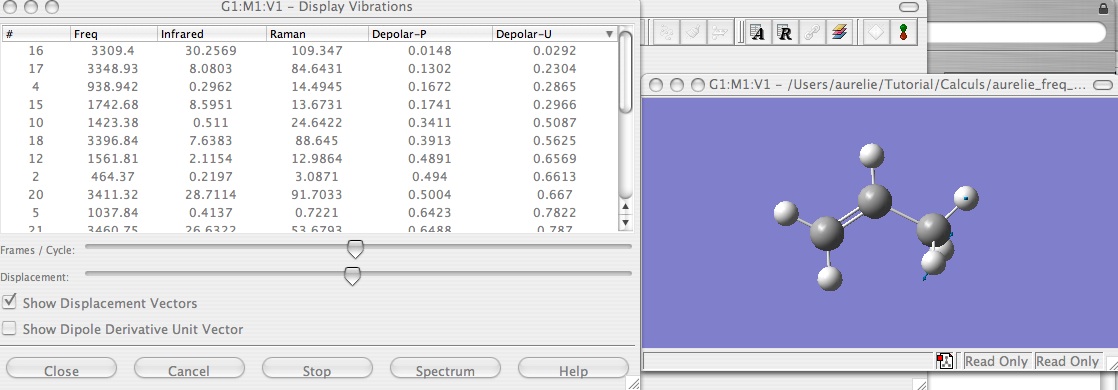The animation enable you to see which are the bond imply in the change of structure in the stationary point.
Our propene
Look at the frequencies of the propene. You might have an imaginary frequency, in this case it is not good news because it signifies that you do not have a minimum but a saddle point, so you have to try to get the real minimum...
In this purpose I propose to you to observe with the animated frequencies what atoms groups are involved in the imaginary frequency. In fact it is the CH3 group which implies a symmetry and thus give this imaginary frequency. So you have to break this symmetry. In this aim you can rotate this CH3 group in order to put the H not in a symmetric place. Or you can change the angle between the double and the single bond in order to break the symmetry too.
In both cases, after optimization and frequencies calculations you have to get no imaginary frequency, so you got the real minimum with this energy :
Sum of electronic and zero-point Energies= -117.827476 Sum of electronic and thermal Energies= -117.823399 Sum of electronic and thermal Enthalpies= -117.822455 Sum of electronic and thermal Free Energies= -117.852478
Check part
Just to be able to check, this is the output file of optimization and frequencies calculation of propene before breaking the symmetry Media:aurelie_opt+freq_dft2_propene.log , and this one is the same but after breaking symmetry : Media:aurelie_opt+freq_dft2_distort_propene.log.
Now you can try to use all your knowledge in the Next part : Suggestion of a transition state between propene and cyclopropane
Back to Resgrp:comp-photo-c3h6-tutorial
Or go to : Some other methods : MPn, CCSD
The theoretical Background
Use Gaussian website : User's reference online
Unix reminder