Exercise 2 : Symmetry properties of molecular vibrations and molecular orbitals

Introduction

In the spectroscopy of a molecule that has symmetry, one observes transitions between states with well-defined symmetry properties.
For example, in vibrational spectroscopy, in the case of a molecule with an inversion centre $i$ , one sees transitions in the IR only for vibrations that are anti-symmetric under inversion, while those vibrations that are symmetric under inversion are seen in the Raman spectrum.
Thus spectroscopy can often give information about the symmetry of a molecular system. In order to interpret spectra of inorganic systems, arguments about the symmetry of the MOs (in the case of UV spectroscopy) or the symmetry of the vibrations (in the case of IR spectroscopy) are often used. The purpose of this exercise is to examine the symmetries of some molecular vibrations and MOs for some simple systems.

What do we mean by the symmetry of a vibration?
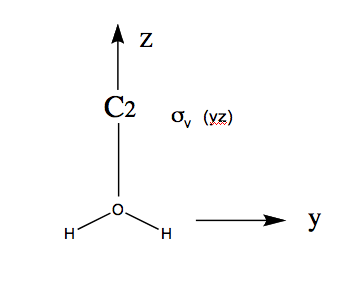
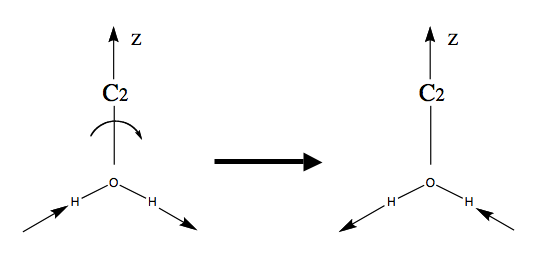
A simple example illustrates the main ideas. Three possible internal vibrations of $H_{2} O$ (numbered 1 to 3) are sketched below together with the symmetry operations in point group $C_{2 v}$ .

If one rotates vibration 1 around the $C_{2}$ ( $z$ ) axis, it is superimposeable. But on performing the same operation on vibration 3, the vibration changes its phase/sign: the arrows point in the opposite direction.

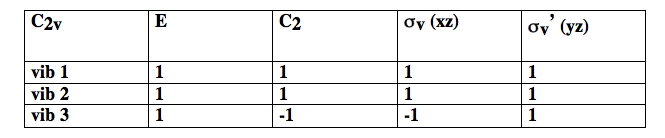
Thus vibrations 1 and 2 are symmetric under $C_{2}$ but vibration 3 is anti-symmetric. We can classify the behaviour of each of these vibrations as symmetric (1) or anti-symmetric (-1) and collect the results as shown in the table below

Vibrations or molecular orbitals that have such well-defined symmetry properties under the operations of a group are said to belong to an irreducible representation (or irrep for short).
As you can see, vibrations 1 and 2 belong to one irrep, but 3 belongs to a different one because it has a different symmetry under $C_{2}$ and $σ_{v} (x z)$ . The set of {1 / -1} for each irrep is called the character of that irrep. Each group has only a small number of possible irrep (i.e. only certain symmetries are possible). In $C_{2 v}$ there are only 4 possible irrep or symmetries that are collected in character tables of the form shown below.

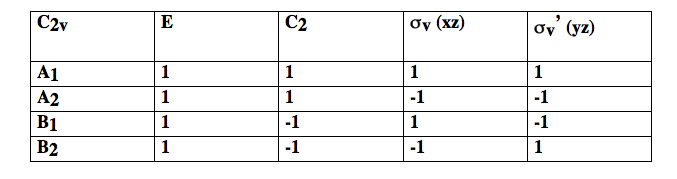
In the first column are labels for the irrep. Thus vibrations 1 and 2 are $A_{1}$ and 3 is $B_{2}$ .

Similar considerations apply to molecular orbital symmetries. One of the bonding MOs in $H_{2} O$ is a mixture of an O $p_{y}$ and an antisymmetric combination of 2 H $1 s$ orbitals as shown below

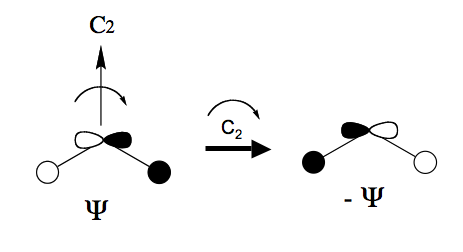
If it is transformed under a $C_{2}$ rotation it changes sign as shown above. You should be able to verify that it has symmetry $B_{2}$ .

Vibrations and MO symmetries of $H_{2} O$ : Demonstration

Symmetry of B2 vibration in H2O

From your ex2 directory,

open the file h2ovibmo_updated.fchk from the File->Open pull-down menu. (Change File type to ‘Gaussian Formatted Checkpoint Files *.fchk’ from exercise 1)

select Vibrations from the Results menu. You will see the frequencies of the vibrations of the molecule (in $c m^{- 1}$ ). The lowest energy vibration is selected by default. You can choose to show displacement vectors, start an animation and adjust the displacement. You should see that is the same motion shown as vibration 1 above.

You may also find it useful to turn on View->Cartesian Axes, and to look along an axis if it's the principal axis.

display the 4391 $c m^{- 1}$ vibration. Sketch the form of the vibration, by drawing arrows to show the nature of the nuclear motions. (GaussView may draw these for you in which case you can use them directly - but bonds may hide some of the displacement vectors). Determine the character (1 or -1) of the vibration under the symmetry operations, and complete the following table, which is reproduced in the data sheet.

==> Complete data sheet

Close the Display Vibrations window when you are finished.

Symmetry of homo-2 in $H_{2} O$

Select Edit->MOs. Select orbital 3 from the MO list (highlights it yellow). Click the button Visualise (not Calculation), then Update.

You should be able to see that this orbital has the same symmetry as the sketch given above and that it has the symmetry properties given below.

Save an image of this MO that demonstrates that it is antisymmetric with respect to reflection in the xz plane
==> Complete data sheet

(Having calculated the surface for this orbital, you can alternatively display it in the main Gaussview window for the molecule, from the Results->Surfaces menu. For MO=3, select Surface Actions->Show Surface. You can also add xyz axes using View->Cartesian Axes. Having displayed the surface this way, you can also select View->Display Format->Surface, and change Solid to Mesh).

Symmetry of lumo, lumo+1, homo and homo-1 in $H_{2} O$

Determine the symmetries of the remaining orbitals using the procedure described above (Edit->MOs), look up the irrep label in the group theory / character tables,
==> Complete data sheet

$B F B r_{2}$ Vibrations: Exercise

In general, a molecule has $3 N - 6$ internal vibrations where $N$ is the number of atoms. Thus there are 6 vibrations in $B F B r_{2}$ . The molecule has $C_{2 v}$ symmetry. The objective is to determine the symmetry of these 6 vibrations.

open the file bfbr2ns_updated.fchk and animate the display of each vibration in turn. Determine the symmetry and make an image of each, to show how the atoms move. (You do not need to explicitly show how each vibration is affected by each symmetry operation - the irreducible representation summarises this).

==> Complete data sheet

Draw in-plane vibrations with arrows, and indicate out of plane motion with a + or - for each atom that moves.

$B C l_{3}$ Vibrations: Exercise

$B C l_{3}$ must also have 6 internal vibrations but has higher symmetry ( $D_{3 h}$ ). If you examine the character tables for $D_{3 h}$ you will see that there are 2 dimensional irreps labelled E’ and E”. These representations are associated with 2 fold degeneracy, which becomes possible for point groups that have a 3 fold rotation axis or higher (explained in more detail below). In this case, one must have E type representations and consequently degeneracy.

open the file bcl3.fchk animate the display of each vibration in turn. Determine the symmetry and make an image of each

==> Complete data sheet

The non-degenerate vibrations are those with frequency 536 and 600 $c m^{- 1}$ . You should analyse these in full first.

The remaining vibrations are in 2 approximately-degenerate pairs (313,313) and (1085,1085). For both vibrations in a pair, you should compute the character for
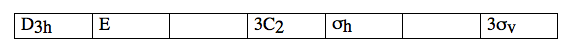
and then add up the result, comparing with the character table. This will distinguish between E’ and E” irreducible representations, and allow you to complete the rest of the table.

NB
Make sure you use the same $C_{2}$ axis and $σ_{v}$ reflection plane for both degenerate vibrations. The computer model of the molecule is not exactly symmetric, but one of the $C_{2}$ axes is likely to make your assignment easier.

For vibrations associated with E symmetry:

For each component of the degenerate pair, reflections, inversion and $C_{2}$ are associated with characters of +1 or –1, but the total character of the E representation is the sum of the characters associated with each of the degenerate pair of vibrations. The total must always be zero for $C_{2}$ and $σ_{v}$ . Consequently we can resolve the degenerate vibrations into vibrations that are symmetric and anti-symmetric components.

The character under $S_{n}$ or $C_{n}$ etc is never + or -1. Under these operations the degenerate pair are simply transformed among themselves. The character under the E (identity) operation is always 2.

The character under $σ_{h}$ determines whether the degenerate pair of vibrations is E’ or E”, and hence the rest of the table for $B C l_{3}$ can be completed

==> Complete data sheet

Correlate the vibrations of $B F B r_{2}$ with those of $B C l_{3}$ . (i.e. attempt to find the vibration in $B C l_{3}$ that most resembles the corresponding vibration in $B F B r_{2}$ )
==> Complete data sheet

One might expect that the vibrations of $B F B r_{2}$ are $B C l_{3}$ are very similar. You should discover that you can match up a pair of degenerate $B C l_{3}$ vibrations with a very similar pair of non-degenerate vibrations in $B F B r_{2}$ . This is a general feature: $C_{2 v}$ is a subgroup of $D_{3 h}$ , the degenerate representations of $D_{3 h}$ become non-degenerate when considered as representations of $C_{2 v}$ .

Symmetry properties of the bonding orbitals in $C r (C O)_{6}$ : Exercise

The highest occupied and lowest unoccupied sets of MOs in transition metal complexes have very predictable forms and occur in doubly and triply degenerate sets, because of the high point group symmetry ( $O_{h}$ ). In this exercise we look at the symmetry of the orbitals that result from the interaction of the Cr p and d shell orbitals with the CO ligand $σ$ and $π$ orbitals. In each example studied, the objective is to determine the symmetry of the orbitals and to relate this to the bonding interactions involved (e.g. which $σ$ vs $π$ orbitals of the ligand match the central atom symmetries).

The Cr atom in $C r (C O)_{6}$ is usually considered to have 6 d electrons in 3 triply degenerate, doubly occupied d orbitals that are essentially non-bonding: shell B in the correlation diagram below. The remaining 2 d orbitals interact with the ligand $σ$ orbitals to form bonding and anti-bonding doubly degenerate sets A and A* in the diagram below. The non-bonding ligand $π$ orbitals interact to form another triply degenerate set C, which interacts only very weakly with the Cr 4p orbitals. The order of the set C and A* depends upon the complex considered and there are many other $σ *$ orbitals that intervene energetically between the B-C and C-A* that we will not be concerned with.

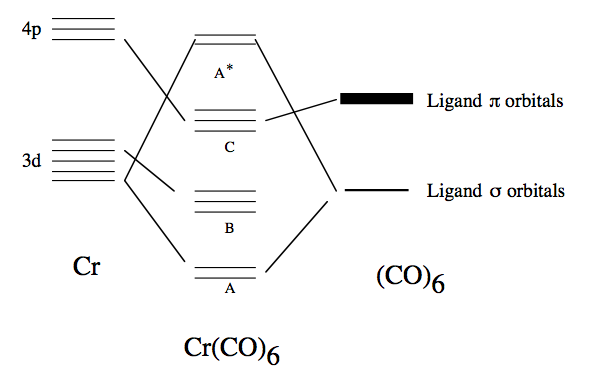
Because these frontier orbitals are degenerate they only have simple symmetry properties under simple symmetry operations such as reflections, inversions and $C_{2}$ operations as we have seen in the previous exercise. The classification of the central atom orbital into the irrep of $O_{h}$ can be obtained from group tables. In the correlation diagram above, only orbitals that have the same symmetry can interact. Thus if one has determined the symmetry of the Cr orbitals (from group theory / character tables) then the symmetry of the ligand orbitals is determined. It remains only to examine nature of the bonding.

Classification of central atom d and p orbitals

consult the character tables: lookup $p_{x}$ , $d_{x y}$ etc (right hand columns), find the irreducible representations these orbitals transform as, and

==> Complete data sheet

Symmetries of frontier orbital sets A B C A*

open the file crco.fchk and display the MOs of each orbital set listed in the data sheet in turn.

==> Complete data sheet

For each MO set you are asked to identify the central atom type (i.e. $d_{x y}$ etc) and the nature of the ligand bond (eg $σ$ CO or $π$ CO). The overall symmetry of the MO can then be deduced from the orbital symmetries determined above. Experiment with the Isovalue (cutoff) when visualising orbitals: it may be easier to see the ligand interactions with higher values (smaller spatial extent) than the default 0.02).

Back to Symmetry Lab

Back to Exercise 1 : Point groups - symmetry elements and operations

Introduction

Vibrations and MO symmetries of H2O : Demonstration

Symmetry of B2 vibration in H2O

Symmetry of homo-2 in H2O

Symmetry of lumo, lumo+1, homo and homo-1 in H2O

BFBr2 Vibrations: Exercise

BCl3 Vibrations: Exercise

Symmetry properties of the bonding orbitals in Cr(CO)6 : Exercise

Classification of central atom d and p orbitals

Symmetries of frontier orbital sets A B C A*

Vibrations and MO symmetries of $H_{2} O$ : Demonstration

Symmetry of homo-2 in $H_{2} O$

Symmetry of lumo, lumo+1, homo and homo-1 in $H_{2} O$

$B F B r_{2}$ Vibrations: Exercise

$B C l_{3}$ Vibrations: Exercise

Symmetry properties of the bonding orbitals in $C r (C O)_{6}$ : Exercise