Exercise 1 : Point groups - symmetry elements and operations

Introduction

Definitions

A symmetry operation is defined as an operation which, when performed on a molecule, leaves the molecule in an indistinguishable state.
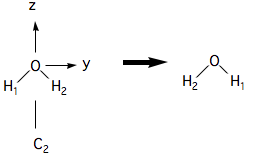
Thus a $C_{2}$ (180˚ rotation) about the $z$ axis in $H_{2} O$ leaves the molecule unchanged:

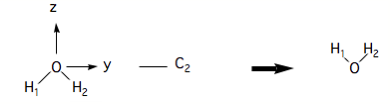
We have added labels to the H atoms so that one can see the result of the operation. A 180˚ rotation about the $y$ axis is not a symmetry operation, however:

because the result of the operation is not superimposeable on the original. In finding symmetry operations one needs to develop some skill with 3-dimensional visualisation. In this exercise you will use the graphics display of Gaussview to manipulate molecular models and identify symmetry operations.

The complete set of symmetry operations of a molecule form a group.
What this means is that performing any two operations in succession is equivalent to performing a third operation, which is also a symmetry operation.

$σ_{v}^{2} = C_{3} \circ σ_{v}^{3}$

(Notice the convention whereby the molecule moves but the symmetry elements are fixed in space).
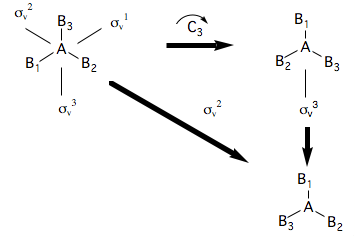
Because symmetry operations can be combined as shown above, in order to identify the group of all symmetry operations of a molecule, one need only identify certain key operations. These operations are called generators. Thus the group of a planar $A B_{3}$ molecule is $D_{3 h}$ and has the following types of symmetry operation.

$D_{3 h} = {E 2 C_{3} 3 C_{2} σ_{h} 3 S_{3} 3 σ_{v}}$

where the symbol $3 C_{2}$ is used to denote the fact that there are 3 equivalent $C_{2}$ rotation axes about each AB bond. A set of generators is

$D_{3 h} g e n e r a t o r s {C_{3} \to S_{3} \to C_{2} \to σ_{h}}$

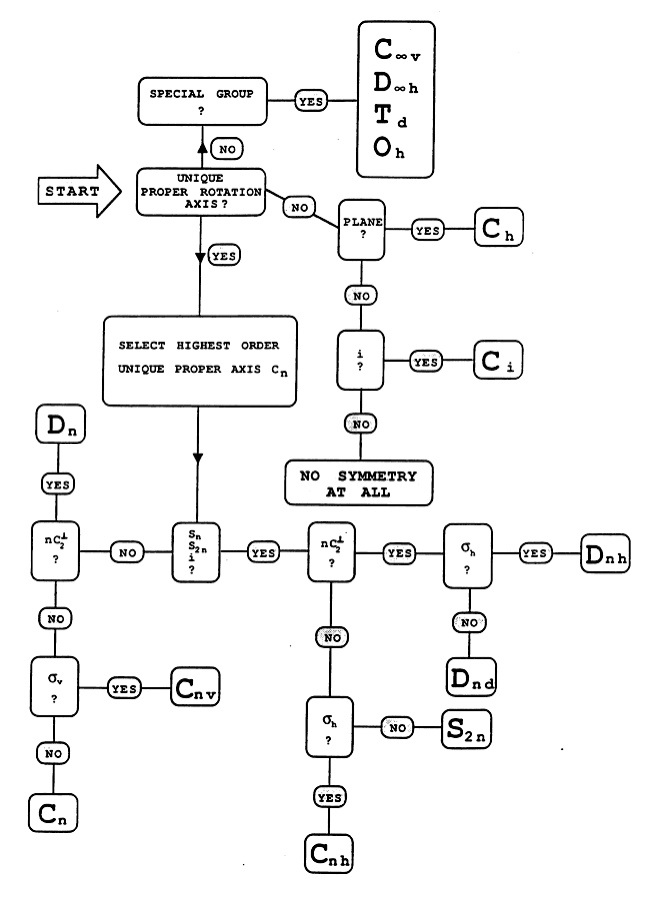
Flowchart

All the other symmetry operations are combinations of this sub-set. The process of finding the generators can be made systematic using a decision table or flowchart, such as the one given below.

NB
The flowchart also indicates that there are relationships between point groups; they do not exist in isolation.

The flowchart is available in a .doc file : Media:flowchart.doc (If you want to print it).

Objective of Exercise 1

The objective is to identify the symmetry operations and assign the point group of following 6 molecules:
1- Chlorocubane (1_CHLOROCUB_updated.com)
2- all trans perhydrotriphenylene (2_PROPELLOR.com)
3- cyclo-octatetraene (3_CYCOCTTET_updated.com)
4- hexavinylbenzene (4_HEXVINBENZ_updated.com)
5- S8 crown (5_S8-CROWN_updated.com)
6- diclorodibromocyclohexane (6_BRCL_CYCHEX.com)

Procedure
a) By examining the molecule in various orientations on the screen, work through the flow chart given above: assign the generators and ultimately the point group for each molecule
==> Complete data sheet
b) Consult the point group tables and identify the remaining symmetry elements in the group. (The ones that were not needed to assign the point group using the flowchart).
==> Complete data sheet
c) Hence make a note of all of the elements of the point group
==> Complete data sheet
Save images of the computer screen with various orientations, and produce several labelled diagrams for each molecule that shows each symmetry operation of the group. (Several symmetry operations could be shown on the same diagram). The aim is to document how you arrived at your point group assignment.

Performing symmetry operations on the computer screen: A demo with cyclohexane

You should first spend a little time familiarising yourself with the Gaussview interface. The files you will use for this exercise are input files (extension .com) for the Gaussian molecular structure program.
Select File->Open, and make sure the File Type is set to ‘Gaussian Input Files *.com’ and that you are in your ex1 directory. Open 0_CYCLOHEX.com.

Mouse buttons :

left: rotates about axes in the plane of the screen
middle: translate
right: rotate perpendicular to the screen and scale

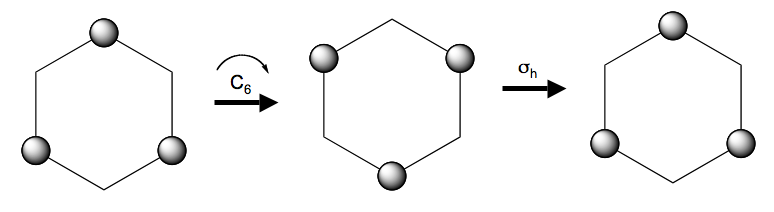
By rotating the molecule from its starting position, you should see a hexagon

where the • indicate C atoms that are nearer to you. (Make small rotations around the other axes to convince yourself of this).

Work through the flowchart as described below.

Look down the principal axis of rotation. Is it $C_{6}$ (i.e. $\frac{1}{6}$ of a turn)? No! This would take an up C atom (•) into a down C atom (no •). It is $C_{3}$ . Turn to the Flowchart. You have identified the decision in the “SELECT HIGHEST ORDER...” box.

Advice Break

To help with this, you can open more than one copy of the same structure (open the 0_CYCLOHEX.com file again in another window), and number the atoms (add labels using View->Labels).

Doing this for the

$C_{3}$

operation will show that the molecule can be moved, but end up in an indistinguishable state.

Clicking within a window may accidentally add a $C H_{4}$ group to the molecule you’ve opened: undo this with Edit->Undo.

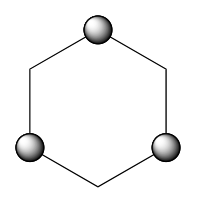
The next decision involves identifying an $S_{2 n}$ , $S_{n}$ or $i = S_{2}$ operation. In this case we have identified n=3 (from the $C_{3}$ ). Do we have an $S_{2 n} = S_{6}$ ? Yes! Remember that $S_{6}$ is a compound operation $σ_{h} \circ C_{6}$ (rotation about an axis, followed by reflection in a plane perpendicular to this axis) as illustrated below.

The $C_{6}$ rotates $\frac{1}{6}$ of a turn, but this is not a symmetry operation. (Try this on the screen by rotating about the axis you are looking down to convince yourself).
The $σ_{h}$ is a reflection at right angles to this $C_{6}$ that brings atoms that are away from you towards you and vice versa. You can always recognise an $S_{2 n}$ from the following figure (i.e. two staggered $C_{3}$ triangles are interchanged).

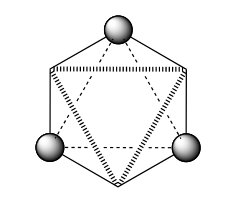
The next decision involves identifying the existence of a $C_{2}$ axis that is at 90˚ to the principal axis $C_{3}$ .

To see this more clearly rotate the molecule so that you are looking at it from the side

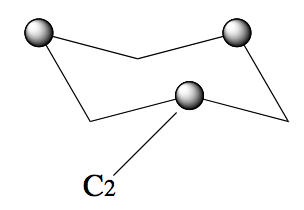
Then rotate about the

C_{2}

axis. There are two indistinguishable states.

The last decision involves the identification of $σ_{h}$ . Clearly since the molecule is not planar, this is not a symmetry operation, so the group is $D_{n d}$ where n=3, thus $D_{3 d}$ .

From the point group tables (click here and select point $D_{3 d}$ group), the additional symmetry elements are $E$ (identity), $i$ (inversion) and $3 σ_{d}$ (diagonal reflection planes; written $s_{d}$ on the website given).

You should now be able to assign point group symmetry to molecules 1-6 above, identifying the key symmetry elements, and the operations that can be generated from them.

Back to Symmetry Lab

Next part Exercise 2 : Symmetry properties of molecular vibrations and molecular orbitals