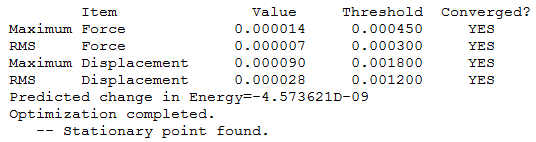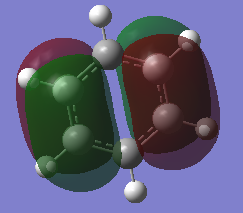EX3section yw7216

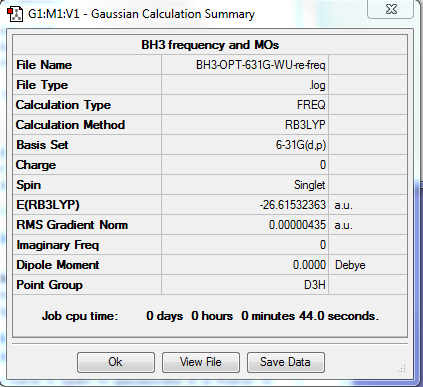
BH₃

Optimisation

Method Used

RB3LYP

Basis Set

6-31G(d,p)

Point Group

D₃H

Summary Table

E(BH₃)

-26.61532363 a.u.

Item table

Frequency.log file

The optimisation file is link to BH3-opt-yw7216-freq.LOG

Low Frequency

Low frequencies ---   -2.3743   -1.0822   -0.0054    2.0836   10.1948   10.2521
 
Low frequencies --- 1162.9856 1213.1754 1213.1781

Jmol image of BH₃

BH3

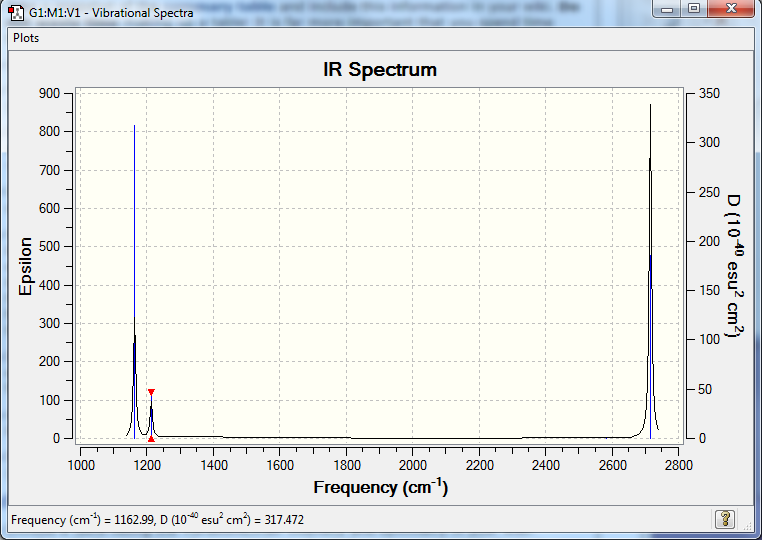
BH₃ Vibrational Spectrum

wavenumber (cm1)	IR intensity	Symmetry	IR active	mode
1162	92	A2	yes	out of plane bending
1213	14	E'	slight	bending
1213	14	E'	slight	bending
2582	0	A1'	no	symmetric stretching
2715	126	E'	yes	assymetric stretching
2715	126	E'	yes	assymetric stretching

There are 6 vibration modes which obeys the 3N-6 rule, but only three peaks are shown in the IR spectrum is because the symmetric stretching is not IR active. And there are two similar bending modes (1213) and two similar assymetric stretching modes (2715) that will combine to one and to give a larger absorption.

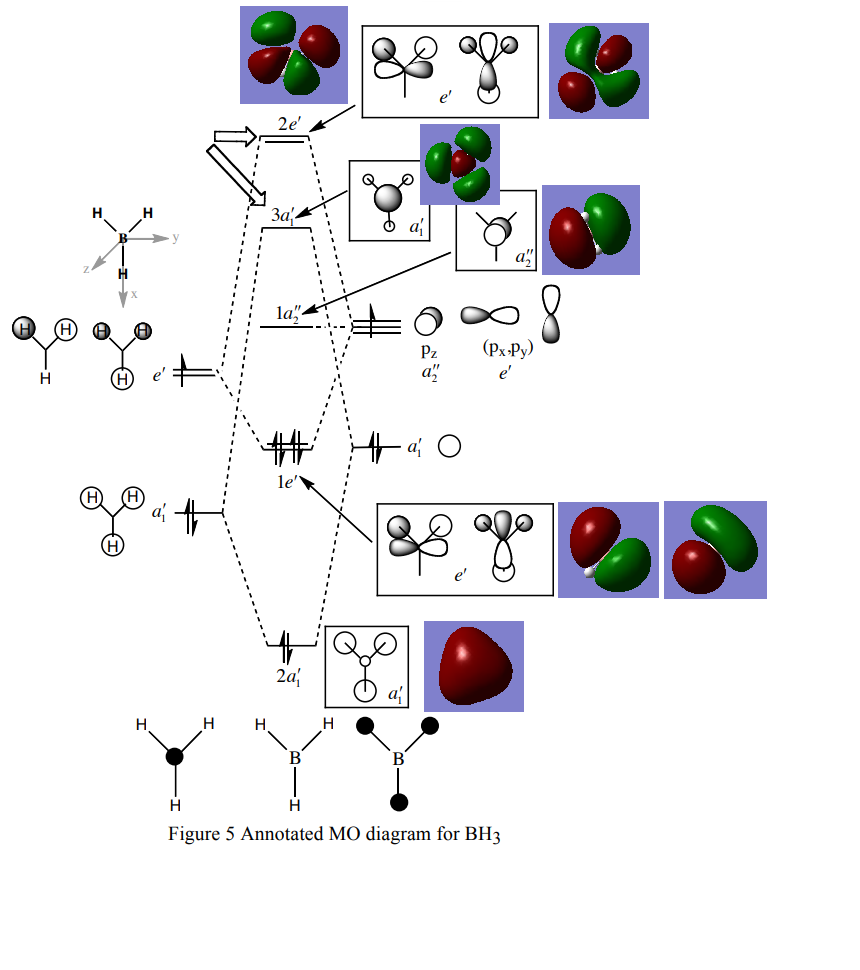
MO diagram of BH₃ ^[1]

There are almost no difference between the LCAO MOs and the real MOs, which means the qualitative MO is accurate.

Calculation of Dissociation energy

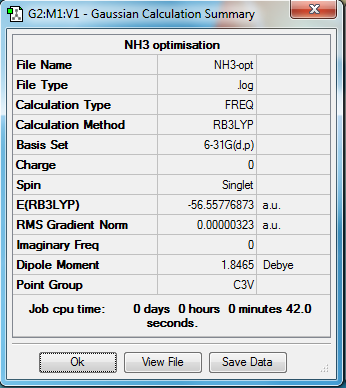
NH₃ optimisation

Method Used

RB3LYP

Basis Set

6-31G(d,p)

Point Group

C₃V

E(NH₃)

-56.55776873 a.u.

Summary Table

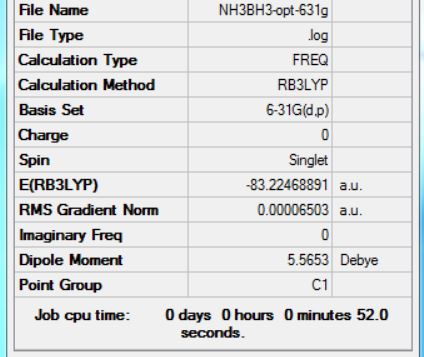
NH₃BH₃ optimisation

Method Used

RB3LYP

Basis Set

6-31G(d,p)

E(NH₃BH₃)

-83.22468891 a.u.

Summary Table

Ng611 (talk) 13:11, 22 May 2018 (BST) Good calculations, but there's some key data missing here. We need to see your frequency log files, low-frequency modes and Jmol images too.

calculation

ΔE= E(NH3BH3) - E(NH3)-E(BH3)
  = - 83.22468891 - (-56.55776873) - (-26.61532363 )
  = - 0.05159655 a.u. = -135.44 KJ/mol

Dissociation Energy = 135.44 KJ/mol

Ng611 (talk) 13:12, 22 May 2018 (BST) The final value should be reported to the nearest kj/mol

BBr₃

Optimisation

Method used

RB3LYP

Basis Set

Gen

Ng611 (talk) 13:13, 22 May 2018 (BST) This should be LANL2DZ, as Gen is not a valid descriptor here.

Summary Table

Item Table

Frequency Analysis

Method Used

RB3LYP with Full NBO

Basis set

Gen

Summary Table

Item Table

Low frequency

Link DOI:10042/202360

Aromaticity : Benzene & Borazine

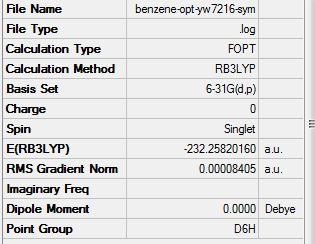
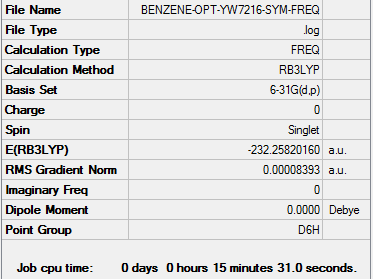
Benzene

Optimisation

Method Used

RB3LYP

Basis Set

6-31G(d,p)

Point Group

D₆H

E(Benzene)

-232.25820160 a.u.

Summary Table

Item Table

[[File:Itemtable-benzene-opt-yw7216-sym.PNG

Frequency Analysis

Method Used

RB3LYP with full NBO

Basis Set

6-31G(d,p)

Summary Table

Item Table

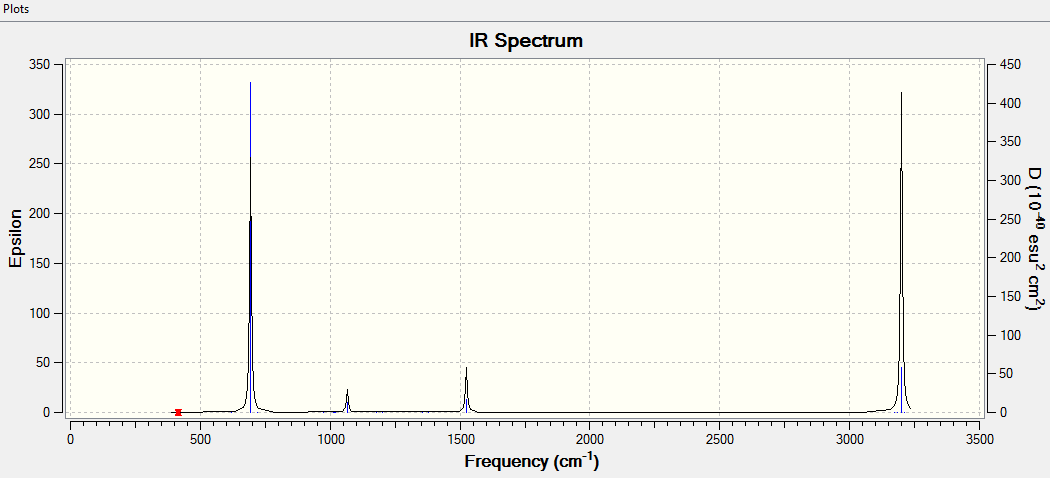
Low frequency

Low frequencies ---  -16.9682  -14.6636  -14.6636   -0.0055   -0.0055    0.0005
Low frequencies ---  414.1239  414.1239  620.9400

Jmol image of Benzene

BH3

The optimisation file is link to Benzene-opt-fre-YW7216

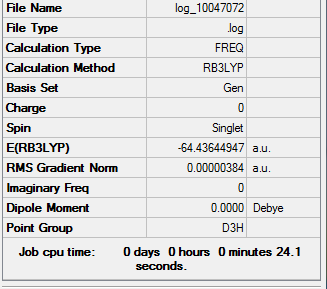
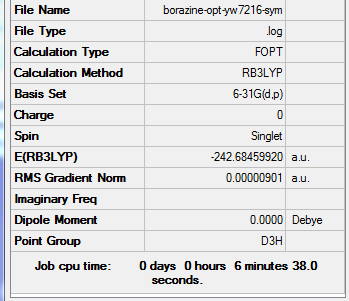
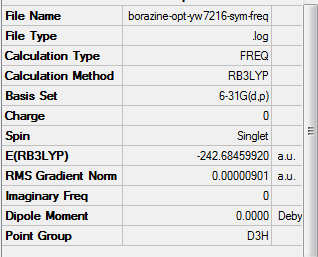
Borazine

Optimisation

Method Used

RB3LYP

Basis Set

6-31G(d,p)

Point Group

D₃H

E(Borazine)

-242.6849920 a.u.

Summary Table

Item Table

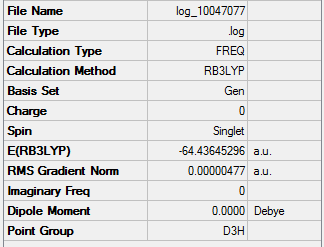
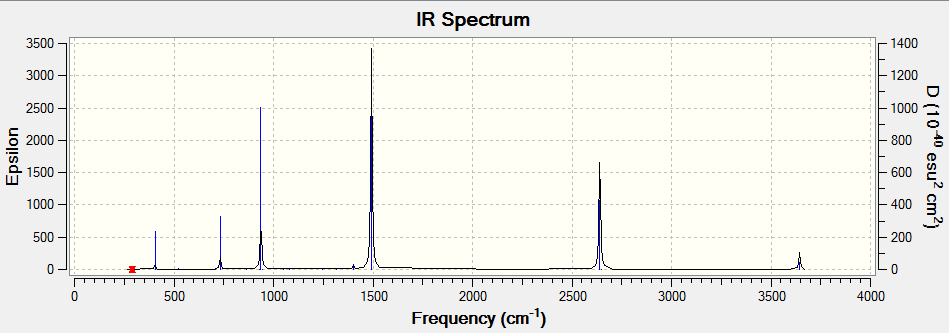
Frequency Analysis

Method Used

RB3LYP with full NBO

Basis Set

6-31G(d,p)

Summary Table

Item Table

Low frequency

Low frequencies ---   -4.7174   -4.6933   -3.9604   -0.0030    0.0036    0.0051
Low frequencies ---  289.7324  289.7331  404.5466

Jmol image of Borazine

BH3

The optimisation file is link to Borazine-opt-yw7216

Ng611 (talk) 13:15, 22 May 2018 (BST) We need the frequency log file, rather than the optimisation log file. They are significantly different and not interchangeable.

Charge Analysis

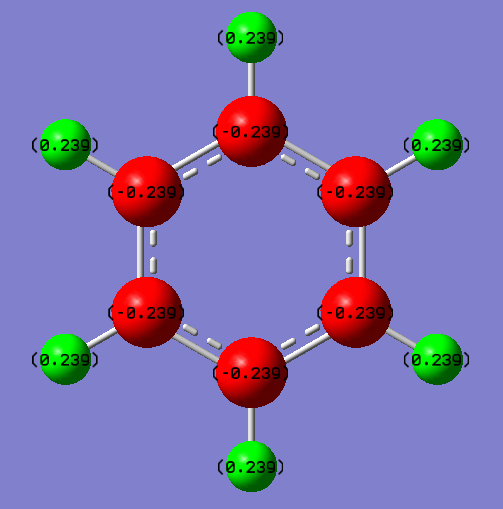
Benzene

Atom	Electronegativity	Charge/a.u.
C	2.5	-0.239
H	2.1	+0.239

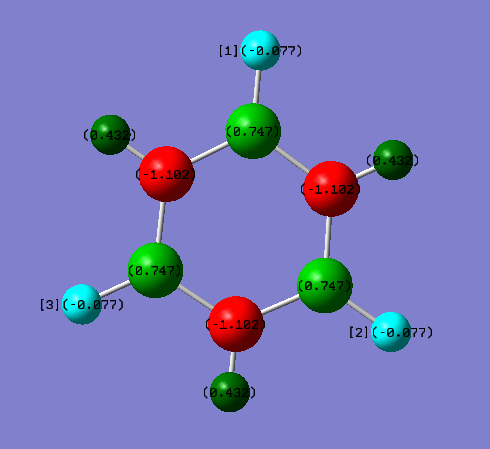
Borazine

Atom	Electronegativity	Charge/a.u.
B	2.0	+0.747
N	3.0	-1.102
H（bonded to B）	2.1	-0.077
H (bonded to N)	2,1	+0.432

Ng611 (talk) 13:18, 22 May 2018 (BST) Good calculation. Remember to use the same colour scale for both benzene and borazine though, for ease of visual comparison.

The charges on the carbon atoms and hydrogen atoms of benzene are evenly distributed, while C is (-0.239 a.u.) and H is (+0.239). But the distribution between hydrogen and carbon is not evenly because of their differences of electronegativities (C 2.5, H 2.1). C is more electron negative therefore it will attract more electron density towards itself between the C-H bond, which leads to the negative charge on itself.

The charges on all the B atoms are evenly distributed and also the same as all the N atoms. But it is not even between B and N atoms, because N is more electronegative (3.0) which attracts more electron density. Therefore N has a negative charge (-1.102 a.u.0) but B has a positive charge (+0.747). And not the H on the borazine has the same charge due to the atoms they are bonded to. Those bonding to B has a very slight negative charge (-0.077 a.u.). And the hydrogens bonding to N has strong positive charge (+0.432 a.u.)

The difference of charge distribution between benzene and borazine is due to the atoms on the main ring. For benzene, the ring is made of carbon atom only. But for borazine, it is made of both boron and nitrogen.

Ng611 (talk) 13:18, 22 May 2018 (BST) Good discussion of the effects of electronegativity on the overall charge distribution. What do the partial charges sum to, and is there any difference in partial charge for atoms related by symmetry? You've alluded to it a bit in your explanation, but I'd say you need to be a bit more explicit.

MO comparison

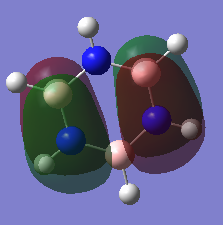
Benzene NO.7 MO (left) & Borazine NO.7 MO (right)

These two orbitals are bonding sigma orbitals. The benzene one has a C₆ rotational axis which is the principal axis and the borazine one has a C₃ rotational axis.

The MO of benzene is evenly distributed but that of borazine is not, which proved the charge density on the hydrogen atoms on the borazine is not the same.

Benzene NO.14 MO (left) & Borazine NO.17 MO (right)

These are the bonding pi orbitals. The MO of benzene is very symmetrical (with a C₆ rotational axis) while that of borazine is not due to the larger contribution on N than B.

And the hydrogens bonded directly to B has no contribution at all.

Benzene NO.20 MO (left) & Borazine NO.20 MO (right)

These are the antibonding pi orbitals. The MO of benzene has a C₂ rotational axis but borazine doesn't.

The reason is same as the NO.17 MO of borazine, the N has a larger contribution to the MO than B.

Ng611 (talk) 13:23, 22 May 2018 (BST) Well done for comparing the correct MOs by shape and not energtic ordering (which is not necessarily reliable). I would include a brief discussion of the overall symmetry and electronegativity differences between the atoms in the molecule to improve this section further. Perhaps also consider dicussing the constituent AOs that form the MOs and the overall symmetry of the MO.

Aromaticity does not only mean flat and cyclic compounds, but also has to obey the Huckel's Rule (has 4n + 2 pi electrons). And the large pi-bond in the middle of the ring is the sharing of the delocalised pi electrons. The aromaticity was indicated by the large, even and diffused real MO (contribution).

Pz AOs are fine to be used for explaining aromaticity of benzene but not other aromatic compounds with heteroatoms (eg.borazine). This is due to the less symmetrical (more distortion) of the AOs in the heteroaromatics are.

Ng611 (talk) 13:23, 22 May 2018 (BST) You're correct in what you've written so far, but a great deal more detail is needed. A detailed discussion on how the modern conceptual model of aromaticity differs from Huckel's model would improve the section further.

Ng611 (talk) 13:23, 22 May 2018 (BST) Some very promising aspects to this report. You let yourself down by leaving out key information (frequency log files, low frequency modes, etc.) though, and your discussion on aromaticity needed more detail. All of your calculations were well performed though, well done.

Reference

[1]Hunt Research Group Molecular Orbitals in Inorganic Chemistry Lecture 4 Tutorial Problem Model Answers