Complab1:zeya1989
Module Introduction
The objective of this module is to computationally model various aspects of organic structure and reactivity, such as to rationalise the outcomes of reactions, to predict feasible modifications or even novel types of reaction. The diversity of such molecular modelling is explored in a range of short experiments and a mini project at the end, through which the following main focuses of this exercise are practiced:
- To use molecular mechanics to predict the geometry and regioselectivity in pre-selected structures in organice reactions
- To use semi-empirical and DFT molecular orbital theory and, to investigate the origins of regioselectivity and neighbouring group participation.
The Hydrogenation of Cyclopentadiene Dimer
Introduction
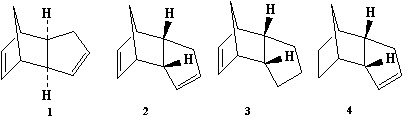
It has been learnt that Cyclopentadiene dimerises through self-Diels-Alder to produce specifically the endo dimer 2 rather than the exo dimer 1[1]. The Hydrogenation of the endo dimer leads to the formation of one of the two possible dihydro derivatives 3 or 4. The modelling technique here employed MM2 force fields on ChemBio3D to optimise the geometries and energies of all four species. The relative energies of the pairs of compounds 1&2 and 3&4 were studied in a thermodynamic sense, i.e. which dimer of each pair is the more stable and/or less strained/hindered. However, the observed reactivity towards cyclodimerisation and hydrogenation can be induced by either thermodynamic (ie product stability) or kinetic (ie transition state stability) contributions. On the basis of the results from the MM2 calculations, it was evidential to determine whether the reactions in question were thermodynamically or kinetically controlled.
Results and Discussion
From the MM2 calculation it was apparent that the exo-dimer 1 (Fig. 1.2.2a) is the thermodynamically more preferred product (energy = 31.8852 kcal/mol), compared to its endo-isomer 2(Fig. 1.2.2b)whose energy is notabaly higher (energy = 34.0001 kcal/mol)due to steric hinderance, with the major contribution from the torsional strain between the 5-membered ring and the bridge. However experimentally,the endo product is favoured. Thus it can be deduced that the thermodynamic factor here is overridden by the kinetic one, i.e. the stability achieved from the 'preferred' relative orientation in which the dienenophile attacks the diene; and as proven, the cyclodimerisation of Cyclopentadiene is indeed kinetically controlled.
| Table 1.1.1 - MM2 optimization data of product 1 to 4 | ||||
|---|---|---|---|---|
| Product | 1 | 2 | 3 | 4 |
| Parameter | Energy / kcal mol-1 | |||
| Stretch | 1.3005 | 1.266 | 1.273 | 1.1023 |
| Bend | 20.5953 | 20.8335 | 19.835 | 14.5239 |
| Stretch-bend | -0.8462 | -0.8379 | -0.8462 | -0.828 |
| Torsion | 7.6334 | 9.5141 | 10.8683 | 12.5064 |
| Non-1,4 VDW | -1.3992 | -1.5318 | -1.2459 | -1.0635 |
| 1,4 VDW | 4.2242 | 4.3092 | 5.6231 | 4.5032 |
For the hydrogenated pair 3 & 4, the thermodynamically favoured product is 4 (energy = 31.1653 kcal/mol), which is more stable than its slightly higher engery isomer 3 (energy = 35.6878 kcal/mol). Hydrogenation on the 5-membered ring is thermodynamically disfavoured, since it raises the total energy by a small but notable amount. In contrast, hydrogenating the C-C double bond on the 6-membered ring reduces the total enrgy by an appreciable amount, as well as reducing vastly the bend energy (by5.312 kcal/mol, which is almost 30% from the alternative 5-membered ring hydrogenation!). Although the latter brings about a slight sizeable rise in torsional strain (from 10.8683 to 12.5064 kcal/mol), this is outweighed by the significant drop in energy associated with bending. Comparing the remaining energy components for 3 and 4 shows that the stretching, and 1,4-Van der Waals energies are reasonably lower in the product 4, while the non-1,4-Van der Waals energy is marginally bigger.
Overall the evidences suggest that porduct 4 is the more stable of the pair and thus the 6-membered ring would be hydrgenated first followed by the 5-membered ring.
Stereochemistry of Nucleophilic Additions to a Pyridinium Ring (NAD+ Analogue)
Introduction
 |
 |
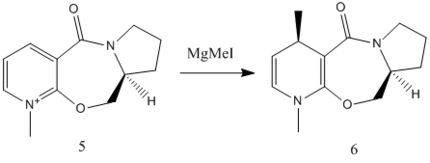
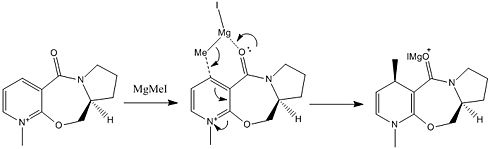
In this exercise two stereoselective reactions are investigated. The first reaction (Fig. 1.2.1a) involves the optically active prolinol derivative (5) which reacts with the Grignard reagent methyl magnesium iodide to alkylate the pyridine ring in the 4-position (para to the Nitrogen atom), with the absolute stereochemistry shown in 6. The only other stereocentre in 6 has a hidrogen atom that is anti to the methyl group on the pyridine ring. In the results section, the 'lower-side' addition refers to the side that is syn to the chrial centre hydrogen and vice versa.
Comparing this Grignard reaction with one involving organolithium reagents shows that the selectivities for the Grignard reaction are enhanced by the relative 'bulkiness' of the reagent, while organolithium reagents lead to random regio and stereo outcome[2].
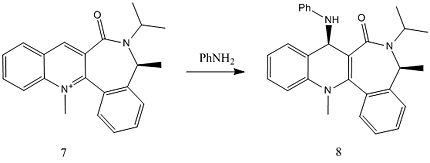
The second reaction illustrates the pyridinium ring of 7 (which displays similar enantioselectivity) [3] reacting with aniline to form the addition product 8 (Fig. 1.2.1b).
Conformational analysis using MM2 force field minimisation of the structures are focused on the geometry obtained in terms of the mechanism (as opposed to the "engergies" of the molecules) and in particular why the methyl/aniline group is delieverd with the stereochemistry shown. The orientation of the carbonyl relative to the plane of the ring is particularly of interest in each reaction, since it can lead to two potential outcome: a) the nucleophile could be drawn to end up on the same side of the ring as the carbonyl via chelation, or b) the addition occurs on the other face of the pyridinium ring as a result of steric repulsion between the carbonyl and the attacking group.
Results and Discussion
| Table 1.2.1 - conformations of 5 and 7 before and after MM2 optimization | ||
|---|---|---|
| Molecule | 5 | 7 |
| Pre-optimization | 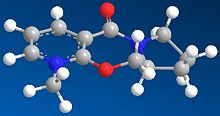 |
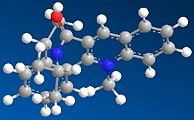 |
| Post-optimization | 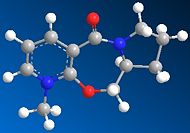 |
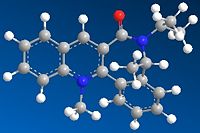 |
| Energy / kcal mol-1 | 43.1179 | 62.5044 |
Several starting configurations of 5 where the carbonyl were manually positioned either below or above the plane of pyridinium ring. MM2 minimisation were run and all the optimised geometry of 5 displayed the same orientation where the carbonyl points slightly upward (approx 10 degrees) from the ring plane and anti to the chiral centre hydrogen, procuding low energy conformations. There had been 'extreme' exceptions where the carbonyl remained below the pyridinium ring after optimisation, however such structures were disregarded as their energies were too high to be of relavence here and also their geometries displayed exceptionally high degree of twisting and distorsion that the molecules did not resemble the actual structure anymore!
In contrast, for molecule 7, all the initial input configurations minimised to yield the final low energy structure where the carbonyl is syn to the chiral centre methyl group. Again, the extreme geometries were not included in the discussion.
From the geometry study above, the reaction mechanisms for both reactions are deduced and illustrated (Fig. 1.2.2a and Fig. 1.2.2b). For the Grignard reaction, the reactants 5 and 6 follow a chelating mechanism, i.e. the carbonyl is chelated by the the Mg and causes the methyl group to move to the upper side of the pyridinium ring.
 |
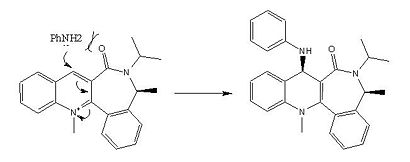 |
The opposite behaviour is demonstrated in the anilination of 7, where the attacking group approaches the carbonyl in the anti fashion. As mentioned in the introduction previously, the selectivity of this reaction results from the steric repulsion between the carbonyl and the nucleophile leading to attack on the anti face.
Further improvements of this model could involve the studies of molecular orbital overlaps and transition states geometries and energies, through which information on HOMO and LUMO of the reactants can be looked at followed by futher deduction on which side of the ring the reaction occurs; transition states on the other hand can provide specific energies for each reaction as an estimate of the kinetics.
Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
Introduction
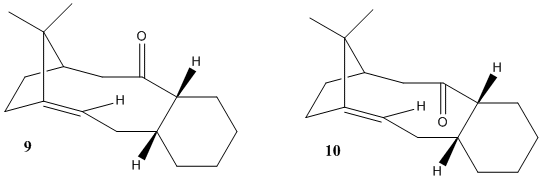
In this exercise the example of atropisomerism in the synthetic intermediates enrounte to Taxol is investigated using MM2 force field minimisations to optimise the structures 9 and 10, in which the carbonyl group points upward and downward respectively (Fig. 1.3.1). Atropisomerism arises in structures of which of general free rotation that are restricted and/or contrained in one of a number of stable configurations that do not necessarily interchange at room temperature[4]. This observation shows that stable isomers do not have to be equally thermodynamically stable to remain in the conformation they are in, since it only needs a significant amount of kinetic barrier to interconversion between them. One of the major factor behind the rigidity of these atropisomers is the presence of the bridgehead alkene, which contributes a sufficient degree of inflexibility to free rotation preventing the molecule to deform interchangebly. The presence of atropisomers makes the sythetic rounte to Taxol nonetheless problematic, due to the difficulty in achieving specific stereoselectivity when reacting with the carbonyl group. Here the energies of the minimised isomers are studied and used to determine which atropisomer is the dominant of the pair and will thence leads to the Taxol synthesis accordingly.
Results and Discussion
| Table 1.3.1 - MM2 optimisations of 9 and 10 | ||
|---|---|---|
| Molecule | 9 | 10 |
| Optimised Structure |  |
 |
| Energy / kcal mol-1 | 48.8749 | 44.2859 |
Reading from Table 1.3.1 it is apparent that molecule 10 has the lower total energy at 44.2859 kcal mol-1, compared to molecule 9 at 48.8749 kcal mol-1. Thus 10 is the thermodynamically more stable atropisomer. From the 3D illustration of 9 it can be seen that a twist-boat conformation is adopted, whereas in 10 the chair conformation is seen.
Both 9 and 10 are examples of hyperstable olefins[4]. They are hyperstable because of the reluctance to undergo hydrogenation across the double bond, which is in contrary to the bond theory convention. Furthermore, the hyperstable alkenes are thermodynamically more stable than their hydrogentated counterparts! This unique property is caused by the increasing strain once the structure is hydrogenated, because the strain exerted by the transformation from sp2 carbons to sp3 carbons will destabilise the already conformationally restricted system, at a degree that the new bond formation could not compensate for.
MM2 is a reasonably good method to optimise simple structures. However it does not always calculate the total minimum of the molecule, and instead it finds the local minimum by 'jiggling' the bonds in the molecule rather than inspecting the effects of moving individual atoms, as this can sometimes results in potential added/reduced strains. If the latter was carried out in an optimisaion the minimum structure obtained would be more accurate.
Regioselective Addition of Dichlorocarbene
Part 1 - Molocular Orbitals of an Assymmetric Chloro-diene
Introduction

Molecular orbital control of reactivity is illustrated in the reaction of compound 12 with electrophilic reagents such as dichlorocarbene, which react together to yield 1,1-dichlorocyclopropane species[5].
This exercise serves to demonstrate the shift from a pure classical mechanical to a quantum mechanical treatment of a molecule. First of all a MM2 force field is used to optimise the geometry prior to applying an electronic method in modelling such a reaction. Then the PM6 method via the ChemBio3D MOPAC interface was employed, which would predict the geometry of 12, as well as providing the graphical display of molecular orbitals and their associated energies. This method is chosen over other such as AM1 because PM6 is the latest proven method that provides accurate approximations. Representations of valence-electron wavefunctions are generated and the HOMO (Highest Occupied Molecular Orbital), HOMO-1 and LUMO (Lowest Unoccupied Molecular Orbital) are discussed with the specific focus of interests in each illustrating the electron density on the alkene bond. Particular attention has been on the HOMO, since it is presumed to be the most reactive towards electrophiles such as Dichlorocarbene.
Results and Discussion
The reaction of 12 with dichlorocarbene is similar to that of an electrophilic addition, and thus the HOMO of 12 should indicate which of the two alkenes (syn or anti, with regards to the projection of the chlorine atom) is the most nucleophilic.
Observation from both the HOMO-1 and HOMO (Fig 1.4.2a and Fig. 1.4.2b) shows that the majority of the electron density are on the syn double bond (along the side to which the Chlorine atom is pointing). On the other hand, in the LUMO (Fig. 1.4.2c) the vast of the elctron cloud is seen to be around the anti double bond, indicating the electron deficient nature of this bond.
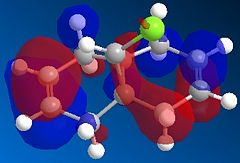 |
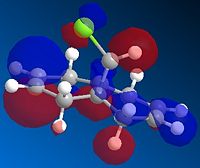 |
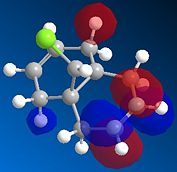 |
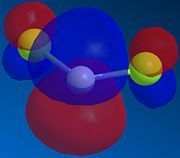 |
Therefore the more favoured alkene in 12 is the endo alkene, since the HOMO shows an significant amount of electron density across the syn double bond. As mentioned above, it is the electrons from the HOMO that determines the alkene's reactivity, via the donation into the electrophile's LUMO. Further probe into the LUMO of dichlorocarbene (the electrophile) provides insight into the symmetry of this orbital (Fig. 1.2.3) - a symmetry that matches that of the endo alkene HOMO along the plane of the ring (assuming it is also the plane of approach in the reaction).
The method used here does not discriminate between the two double bonds explicitly if factors such as sterics and kinetics were to be considered. However this qualitative molecular orbital approach is sufficient here because of the nature of this the reaction.
Part 2 - Vibrations of Chloro-diene and its Dihydro Derivative
Introduction
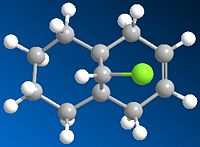
The objective of the second part of this exercise is to investigate and quantify the influence of the Cl-C bond on the vibrational frequencies of this molecule, through comparing between the molecule 12 and its anti monohydrogenated derivative D in which the exo double bond, and 'only' the exo bond is replaced by a C-C single bond (Fig. 1.4.4).
The method used to obtain vibrational data is the DFT (Density Function Theory) B3LYP/6-31G(d,p), following the geometry optimisation procedure as previously used. Gaussian 03 was used to run the geometry opitmisation and frequency calculation via submission on SCAN, as the time it takes to run on the assigned laptop would take much longer. For details of the procedure involved please click HERE.
When the calculations are complete, IR vibratianl data are extracted and presented in the IR spectra below, allowing comparisons to be drawn from the two molecules with regards to frequencies of the Cl-C single bond and the C=C anti double bond.
Results and Discussion
| Table 1.4.1 - Vibrational Data for 12 and D | ||
|---|---|---|
| Bond | 12/cm-1 | D/cm-1 |
| C-Cl | 770.62 | 775.12 |
| C=C(syn) | 1757.54 | 1758.09 |
| C=C(anti) | 1737.27 | N/A |
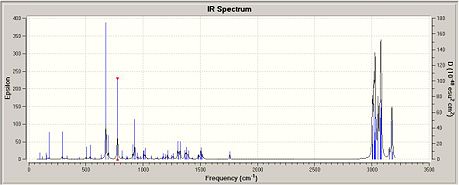
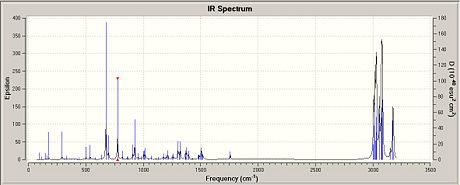
The predicted IR spectra of 12 and D(Fig. 1.4.5a and Fig 1.4.5b) comprises the common vibrations, i.e. symmetrical and assymmetrical stretches, rocking, scissoring, wagging and twisting that are expected and thus need not to be shown. What is important and relavent here are the frequencis of C-Cl and C=C anti-/syn- double bonds in each molecule and hence Table 1.4.1 on the right summerises these data from the vibrational calculation. Reading from the table, it can be seen that the C-Cl bond in D has a higher stretching frequency of 775.12 cm-1 than in 12 (770.62 cm-1). Therefore it can be inferred that the C-Cl bond is stronger in the monohydrogenated drivative compared to the chloro-diene. The explanation behind this novel effect could be due to the absence of the anti C=C bond in D. Theoretically if can be assumed that in 12, the πC=C,anti orbital donates electron density into the σ*C-Cl orbital, and causes the C-Cl bond to weaken. However in D the absence of the C=C anti bond means that it lacks an orbital of the complementary symmetry with similar electron density to allow for such interaction.
 |
 |
For molecule 12, the syn C=C bond vibration is 1757.54 cm-1, which is higher than the anti C=C bond vibration at 1737.27 cm-1, indicating that the syn alkene is stronger than the anti alkene. This observation is in agreement with the electron density predicted for molecular orbitals in Part 1 of this exercise, further confirming that the syn C=C bond is electron rich and hence more nucleophilic compared to the anti alkene.
For the monohydrogenated derivative D, the C=C bond has a strech frequency at 1758.09 cm-1, essentially very similar to that of molecule 12. Hence it is reasonable to deduce that the conversion of the anti carbons from sp2 to sp3 has very little/hardly any electronic effect on the vibrational behaviour of the syn alkene. While the small difference in the stretch frequencies could be accounted by the alteration in geometry, which results in slight distorsion of the overall structure and difficulty in deviation from the syn alkene.
Mini-project: Stereodivergent Synthesis of α-hydroxy-β-amino Isopentanoic Acids[6]
Introduction
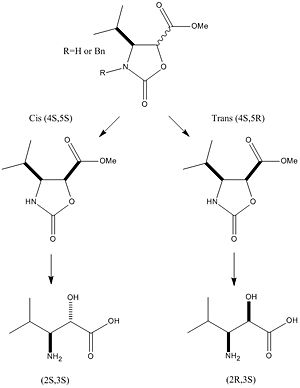
The objective of this mini project is to investigate, using computational modelling, on how to distinguish between two isomers arising from a single reaction, through the analysis of spectral data and insight on the molecular structures.
The reaction chosen is the stereodivergent route to enantiopure α-hydroxy-β-amino isopentanoic acids (2R,3S)-1 (2S,3S)-2 based on the following criteria:
- A relatively small molecule (<25 heteroatoms), such that computing times will be minimised
- Produces two, and only two diasteroisomers
- Produts have literature-recorded 13C NMR data and IR spectra values which can be used for comparisons with the computed spectra.
The two isomers were firstly drawn in the ChemBio3D and followed by MM2 force field optimisation of their structures as a pre-treatment before submitting for Gaussian calculations later on. The energy of isomer 1 was 5.8430 kcal/mol and that of isomer 2 was calculated to be 5.3120 kcal/mol. It is apparent to conclude that based on the total energies of strcutres, isomer 2 is the thermodynamic product of the pair.
13C NMR
Isomer 2S,3S
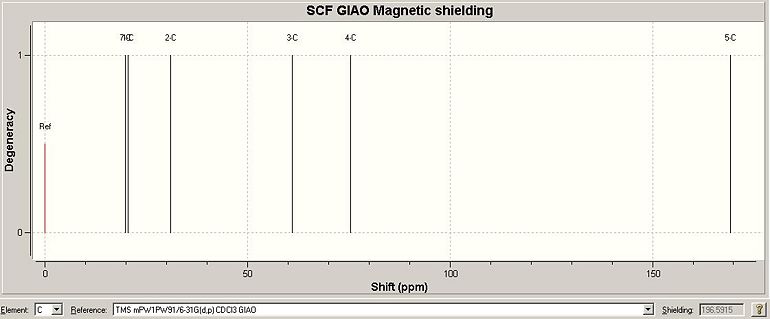
The Gaussian job for NMR calculation was run using the GIAO approach, where DFT-MPW1PW91 optimisation was employed. The carbon atoms are numbered for NMR assignment and is illustrated in Fig. 2.2.1. The solvent was specified in the literature as D2O and therefore in the calculation the solvent was changed to water. The chemical shifts are viewed against CDCl3 reference and displayed in Fig. 2.2.2. Table 1.5.1 summerises the comparison between predicted and reported NMR data. From reading the data, the calculated values are in very good agreement with the literature values.
| Table 1.5.1 - NMR Data for isomer 1 | |||
|---|---|---|---|
| Carbon NO. | Calculated shift/ppm | Literature shift/ppm | Difference/ppm |
| 1 | 18.9 | 18.3 | 0.6 |
| 2 | 33.1 | 29.2 | 3.9 |
| 3 | 54.2 | 49.5 | 4.7 |
| 4 | 77.3 | 70.4 | 6.9 |
| 5 | 170.8 | 174.4 | 3.6 |
| 7 | 23.6 | 19.6 | 4.2 |
Isomer 2R,3S
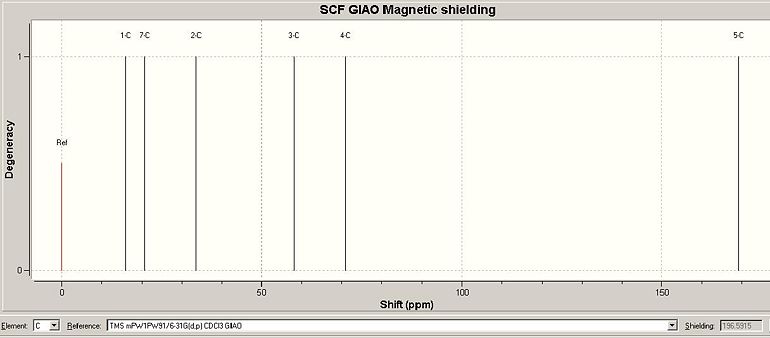
All the calculations were performed as previously described for isomer 1and again, all the values are in a good agreenment with the literature since the difference between the two are < 10ppm.
| Table 1.5.2 - NMR Data for isomer 2 | |||
|---|---|---|---|
| Carbon NO. | Calculated shift/ppm | Literature shift/ppm | Difference/ppm |
| 1 | 20.8 | 17.8 | 3.0 |
| 2 | 31.3 | 28.4 | 2.9 |
| 3 | 56.8 | 49.8 | 7.0 |
| 4 | 70.0 | 71.3 | 1.3 |
| 5 | 173.2 | 174.6 | 1.8 |
| 7 | 20.1 | 15.5 | 4.6 |
IR Vibrational Spectra
The predicted spectra for both isomers are in good agreement with the quoted frequencies of the bonds summarised in the tables below.
Isomer 2S,3S
| Table 1.5.3 - IR Vibrational Data for Isomer 1 | |
|---|---|
| Bond | Stretch/-1 |
| N-H | 3589.37(A), 3498.66(S) |
| O-H | 3812.01(next to N), 3759.55(next to O) |
| C=O | 1851.14 |
| C-O | 1373.97 |
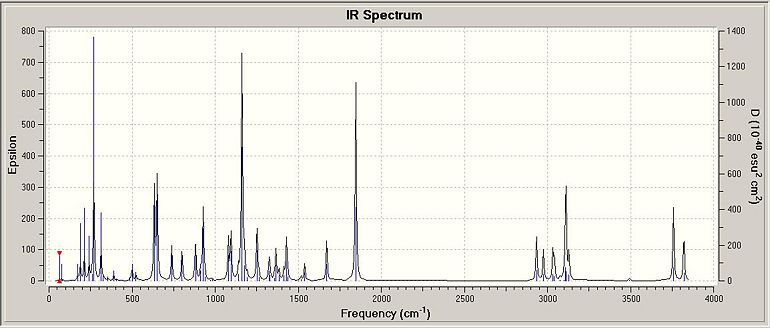
Isomer 2S,3S
| Table 1.5.4 - IR Vibrational Data for Isomer 2 | |
|---|---|
| Bond | Stretch/cm-1 |
| N-H | 3586.35(A), 3503.61(S) |
| O-H | 3819.11(next to N), 3757.60(next to O) |
| C=O | 1837.46 |
| C-O | 1381.98 |
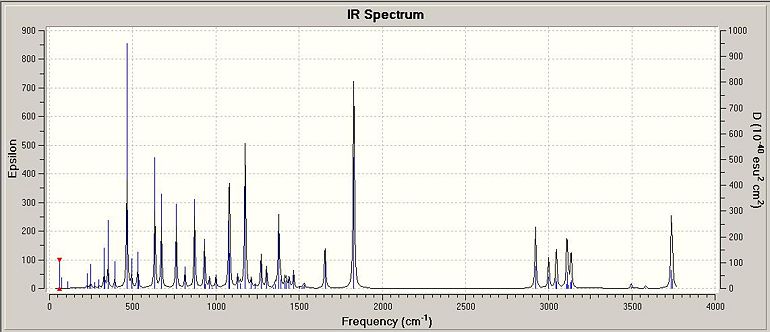
Conclusion
In this project the predicted NMR and IR spectra demonstrated close resemblence to the literature records for both isomers. This is a good indication that the computational method used was reasonablly accurate and provided good approximations of the structures being studied. To further distinguish between to two products, optical rotation values could be calculated and compared to the reported values; however unfortunately such calculations were not carried out in this project due to time constraint.
Module References
- ↑ J. Sauer, R. Sustmann, Angew. Chem., Int. Ed. Engl., 1980 , 19, 779 - 807. DOI:10.1002/anie.198007791
- ↑ A. G. Shultz, L. Flood, J. P. Springer, J. Org. Chemistry, 1986, 51, 838-841. DOI:10.1021/jo00356a016
- ↑ S. Leleu, C. Papamicael, F. Marsais, G. Dupas, V. Levacher, Tetrahedron: Asymmetry, 2004, 15, 3919-3928. DOI:10.1016/j.tetasy.2004.11.004
- ↑ 4.0 4.1 W. F. Maier, P. R. Schleyer, J. Am. Chem. Soc., 1981, 103, 1891-1900. DOI:10.1021/ja00398a003
- ↑ B. Halton, R. Boese, H. S. Rzepa, J. Chem. Soc., Perkin Trans 2, 1992, 447-448. DOI:10.1039/P29920000447
- ↑ W. D. Seo, J. Curtis-Long, Y. B. Ryu, J. H. Lee, M. S. Yang, W. S. Lee and K. H. Park., J. Org. Chem., 2006, 71, 13. DOI:10.1021/jo060309m }}