Calculate the energy of a molecule
Calculate the energy consists in solving the Schrodinger equation, but because an exact solution can not be obtained for most of the molecules, we need to consider some approximations, and thus use different theories.
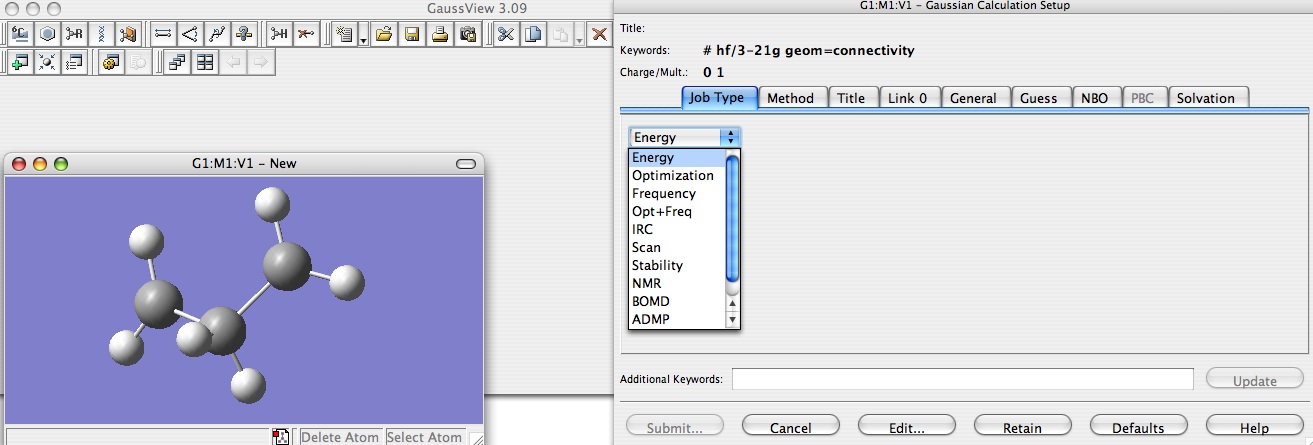
Calculate the energy with the Hartree Fock
Your molecule is drawn, so click on Calculate --> Gaussian, and a new window should appear. Click on Job style and select Energy.
Then click on Method and choose Hartree-Fock with a basis set of 3-21G or 6-31G (of course the basis set 6-31G should be better than the 3-21G but the second could be a good first approximation it depends on the molecule. Notice that you can choose if you want to consider a restricted or unrestricted spin.
Then click on Title and enter the title of your file, and click on Link 0. In this part you have to type your file name after %chk. Then click on Edit and save on Gaussian. A third window should appear, in which you have to enter the file name, take the same as you enter after %chk.
Advice break
I advice you to enter as a file name something like yourname_typeofcalcul_method_nameofmolecule. Thus you can exactly know with just the name of the file what type of calculation it corresponds to and with which parameters.
You created a file .com (check if everything is registering in your folder). Now everything is ready to be calculated by Gaussian.
Open a Terminal window and enter the name of your file, press enter and it would be start the calculation. At the end you should find the results in the file .log that you can open with the TextEdit application.
Calculate the energy with the DFT
Instead of select Hartree-Fock method select of course DFT. Then choose B3LYP, it corresponds to a specific method of DFT. Now you have to choose the basis set, as previously choose 3-21G or 6-31G according to the accuracy that you would like (but keep in mind that the fact that 3-21G has a lower accuracy involves that the calculations would be quick).
Do the same as previously for the Title, Link 0 parts. Click on Edit, save on Gaussian and enter the file name. Make sure that you have good saved. Start to calculate in the Terminal.
As previously a file .log appeared in your folder.
Where is the energy of the molecule in the file .log ?
Try to find the part below in the file, it is just before the population analysis.
I present you below the results for the propene.
Results with Hartree-Fock theory and basis set 3-21G
SCF Done: E(RHF) = -116.417542264 A.U. after 5 cycles
Convg = 0.4947D-04 -V/T = 2.0025
S**2 = 0.0000
With these informations you access to the Energy, and if it converges quickly or not.
Results with Hartree-Fock theory and basis set 6-31G
SCF Done: E(RHF) = -117.021625213 A.U. after 5 cycles
Convg = 0.6933D-04 -V/T = 1.9990
S**2 = 0.0000
Results with DFT and basis set 6-31G
SCF Done: E(RB+HF-LYP) = -117.875270056 A.U. after 4 cycles
Convg = 0.2671D-03 -V/T = 2.0053
S**2 = 0.0000
Have a look at the results with the basis set 6-31G* : it corresponds to consider the d-orbital of the carbon and insert them in the calculation as unoccupied orbitals. (results for the propene)
SCF Done: E(RB+HF-LYP) = -117.903544645 A.U. after 5 cycles
Convg = 0.2824D-04 -V/T = 2.0033
S**2 = 0.0000
I reported the results of the different calculations in the table below.
| Energy | ||||
| HF theory | DFT | |||
| 3-21G | 6-31G | 6-31G | 6-31G* | |
| Propene | -116.417542264 | -117.021625213 | -117.875270056 | -117.9000620915 |
| Cyclopropane | -116.396280646 | -117.003935971 | -117.862099604 | -117.893819782 |
Now compare the energy between cyclopropane and propene with the different method with the experimental data.
| Ecycloproprane - Epropene | Error of | Time of calculation | ||
| Hartree | kcal/mol | % | min , second | |
| HF ; 3-21G | 0.026362 | 16.54241862 | 53 % | 3.9 s |
| HF ; 6-31G | 0.02355 | 14.7778605 | 47 % | 4 s |
| HF ; 6-31G* | 0.015375 | 9.64796625 | 19 % | 7.7 s |
| HF ; 6-31G (d+p) | 0.015326 | 9.61721826 | 19 % | 15.4 s |
| DFT ; 6-31G | 0.020699 | 12.98882949 | 40 % | 32 s |
| DFT ; 6-31G* | 0.013789 | 8.65273539 | 10 % | 1min 1.3s |
| DFT ; 6-31G (d+p) | 0.01389 | 8.7161139 | 10.5 % | 1min 33.4s |
| DFT ; 6-31G (df+pd) | 0.013523 | 8.48581773 | 8 % | 5min 58 s |
The experimental data is 7.8 kcal/mol.
Different methods which were used enable you to see the different results obtained with different methods of approximations. Indeed, 6-31G* indicates that the d orbitals of carbon are considered in the calculation and for 6-31G (d+p) it is the d orbitals of carbon + p orbitals of hydrogene. And (df +pd) d and f orbitals of carbon and p and d orbitals of hydrogene.
As expected better is the basis set better are the results, indeed the better method seems to be DFT 6-31G (df + pd), but the time of the calculation is very huge compared to the other DFT models. So it is simple to understand that a compromise must be done, and because of this I think that the better method that we can use to get the better results is DFT 6-31G*.
Are these calculations usefull?
Obtain the energy of a molecule is of course very usefull, because this energy can give you a lot of informations about the stability of a structure, and so with comparing several molecules you can know where is this structure on it potential energy surface. I aggregated some examples below.
Advice break
Be careful, you can compare some molecules to each other just in case that you put exactly the same parameters by running the calculations. Because if you do not take exactly the same the approximations are not comparable.
if you do not get the same energy it could be simply because you do not have the same geometry of the system. Energy of the table correspond to the geometry of the minimum of the system (which is not obvious to obtain by drawing the molecule especially in the case of propene).
Direct applications
In the two following applications we use the energy to obtain some information concerning the structure of the molecule, so when I speak about Stability of a struture it is linked to the energy. For information concerning the wave function stability look at the part More about the stability of a molecule .
Stability of a structure ?
By running the same calculations methods on several forms of a molecule you can predict what kind of stereoisomers as the lowest energy and so would be more present. For example look at the energy of the three stereoisomers of 1,2-dichloro-1,2-difluoroethane, and check which of them has the lowest energy.
Singlet or Triplet ?
You can know too if the ground state of a molecule is a singlet state or a triplet state for example. In this aim, have a look on the energy of the propene in a singlet and triplet state.
Propene HF 6-31G singulet
SCF Done: E(RHF) = -117.021628058 A.U. after 11 cycles
Convg = 0.9182D-08 -V/T = 1.9990
S**2 = 0.0000
Propene HF 6-31G triplet
SCF Done: E(UHF) = -116.910538298 A.U. after 15 cycles
Convg = 0.1887D-08 -V/T = 1.9942
S**2 = 2.0203
In both case it converges, but the energy of the singlet state in lower than the energy of the triplet state, so the ground state is the singlet.
The other informations
Dipole and higher multipole moments
With Gaussian you can get dipole moments of your molecule too.
Look at this part (calculation run with HF, 6-31G on propene) :
Dipole moment (field-independent basis, Debye):
X= 0.3600 Y= 0.0442 Z= 0.0000 Tot= 0.3627
Quadrupole moment (field-independent basis, Debye-Ang):
XX= -19.5261 YY= -18.7341 ZZ= -21.9200
XY= 0.0389 XZ= 0.0000 YZ= 0.0000
Traceless Quadrupole moment (field-independent basis, Debye-Ang):
XX= 0.5340 YY= 1.3259 ZZ= -1.8599
XY= 0.0389 XZ= 0.0000 YZ= 0.0000
Octapole moment (field-independent basis, Debye-Ang**2):
XXX= -1.7878 YYY= 0.7055 ZZZ= 0.0000 XYY= -0.2256
XXY= 0.8338 XXZ= 0.0000 XZZ= 2.1856 YZZ= -0.8379
YYZ= 0.0000 XYZ= 0.0000
Hexadecapole moment (field-independent basis, Debye-Ang**3):
XXXX= -177.8237 YYYY= -51.6446 ZZZZ= -29.5812 XXXY= -0.3421
XXXZ= 0.0000 YYYX= 0.8729 YYYZ= 0.0000 ZZZX= 0.0000
ZZZY= 0.0000 XXYY= -38.7742 XXZZ= -37.4973 YYZZ= -14.3268
XXYZ= 0.0000 YYXZ= 0.0000 ZZXY= -0.9028
Now compare the dipole moment of propene and cyclopropane.
Charge distribution
Gaussian analyses the Mulliken population too.
Always for propene (HF,6-31G)
Mulliken atomic charges:
1
1 C -0.353356
2 H 0.156926
3 H 0.158833
4 C -0.153634
5 H 0.173968
6 C -0.489681
7 H 0.174627
8 H 0.157689
9 H 0.174627
Sum of Mulliken charges= 0.00000
Thus, with this figures we can deduce that there is no real charge on propene, and we can associate the charge to each atom. So, the C atoms are considered negatively and the balancing positive charge is divided between the H.
But be careful, Mulliken population analysis is quite arbitrary (as the other methods), because it is not a quantum mechanical observable. So just look at this if you want an approximation of the atom's charge.
Advice break
Keep in mind that the results concerning the dipole and the Mulliken population are average results, it is just an approximation, so just consider relative difference between the atom and not the absolute results.
Molecular orbitals and orbital energies
If you put Pop=Reg in the additional keywords section you require data about the molecular orbitals. Took the example of the propene, you should find this in the file .log (with HF and the basis set 6-31G) :
Molecular Orbital Coefficients
8 9 10 11 12
(A)--O (A)--O (A)--O (A)--O (A)--O
EIGENVALUES -- -0.57865 -0.57277 -0.52015 -0.48496 -0.34765
1 1 C 1S 0.00136 0.00000 -0.02273 -0.00410 0.00000
2 2S 0.00128 0.00000 0.05023 0.00830 0.00000
3 2PX 0.04792 0.00000 0.22629 0.18654 0.00000
4 2PY 0.34016 0.00000 0.13823 -0.16817 0.00000
5 2PZ 0.00000 0.05865 0.00000 0.00000 0.37994
6 3S -0.03697 0.00000 0.04624 0.02149 0.00000
7 3PX -0.00546 0.00000 0.08742 0.12442 0.00000
8 3PY 0.14655 0.00000 0.05785 -0.11756 0.00000
9 3PZ 0.00000 0.04030 0.00000 0.00000 0.32425
10 2 H 1S -0.21613 0.00000 -0.06676 0.14606 0.00000
11 2S -0.15552 0.00000 -0.06524 0.11487 0.00000
12 3 H 1S 0.06374 0.00000 -0.07391 -0.17825 0.00000
13 2S 0.03739 0.00000 -0.06917 -0.13833 0.00000
14 4 C 1S 0.00490 0.00000 0.00115 0.01208 0.00000
15 2S -0.00753 0.00000 0.00420 -0.02115 0.00000
16 2PX -0.25775 0.00000 -0.19320 -0.25303 0.00000
17 2PY -0.07346 0.00000 -0.20889 0.22613 0.00000
18 2PZ 0.00000 0.11512 0.00000 0.00000 0.35371
19 3S -0.02314 0.00000 -0.03549 -0.05576 0.00000
20 3PX -0.09927 0.00000 -0.06950 -0.13338 0.00000
21 3PY -0.03889 0.00000 -0.09958 0.16729 0.00000
22 3PZ 0.00000 0.05542 0.00000 0.00000 0.31203
23 5 H 1S -0.04642 0.00000 -0.14509 0.16809 0.00000
24 2S -0.03252 0.00000 -0.11349 0.12367 0.00000
25 6 C 1S -0.00844 0.00000 0.00100 0.01875 0.00000
26 2S 0.01429 0.00000 -0.00277 -0.03976 0.00000
27 2PX 0.05628 0.00000 0.21730 0.28416 0.00000
28 2PY -0.27435 0.00000 0.26484 -0.16098 0.00000
29 2PZ 0.00001 0.42920 0.00000 0.00000 -0.11315
30 3S 0.02771 0.00000 -0.00740 -0.04336 0.00000
31 3PX 0.02699 0.00000 0.11944 0.12974 0.00000
32 3PY -0.12942 0.00000 0.14678 -0.09496 0.00000
33 3PZ 0.00000 0.21293 0.00000 0.00000 -0.09879
34 7 H 1S 0.11309 -0.23337 -0.09680 0.06717 0.08710
35 2S 0.08094 -0.17506 -0.07930 0.06760 0.07711
36 8 H 1S -0.09231 0.00000 0.24466 0.04815 0.00000
37 2S -0.07265 0.00000 0.19945 0.05803 0.00000
38 9 H 1S 0.11310 0.23337 -0.09680 0.06717 -0.08710
39 2S 0.08094 0.17506 -0.07930 0.06760 -0.07711
The eigenvalues give the energy of the molecular orbital. And O signifies that the orbital is occupied, so you can easy know which are the HOMO and the LUMO orbitals because the O becomes V.
In the case of propene (calculation run with HF, 6-31G) we obtain this :
8 9 10 11 12 13 14 15
(A)--O (A)--O (A)--O (A)--O (A)--O (A)--V (A)--V (A)--V
Next part : optimization of the geometry of a molecule
Back to Resgrp:comp-photo-c3h6-tutorial
Or go to : Some other methods : MPn, CCSD
The theoretical Background
Use Gaussian website : User's reference online
Unix reminder