BBC1
Tim Barrett, Chemistry Year Three, Computational Lab 2010
Module One
Section 1A - The Hydrogenation of Cyclopentadiene Dimer
Introduction
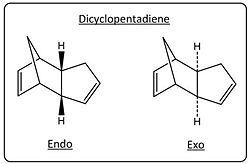
Cyclopenadiene is a cyclic diene consisting of five carbons. At room temperature cyclopentadiene dimerises via a Diels-Alder Reaction to give dicyclopentadiene (this reaction is reversed upon heating: Retro-diels alder).
Diels Alder reactions can lead to the formation of two diastereoisomers; namely the endo and exo products, refering to the orientation of the transition states to which the reaction proceeds.
A rule of thumb for which diastereoisomer will be the major product is known as the endo rule. The endo rule states that the major product will be the one that proceeds through the lowest energy transition state - most usually the endo product. This rule suggests kinetic control through the deciding factor being the transition state energy (activation energy) of the reaction and not the overall thermodynamics. As the endo product is known to be the major product in the reaction described, modelling of both products and calculating their respective energies can be used to see if this indeed the case.
Modelling
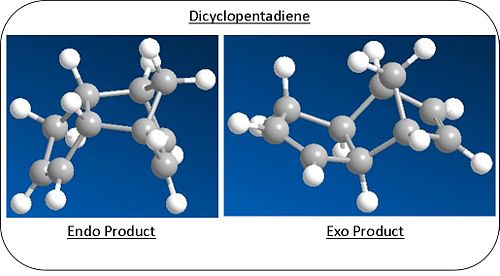
Using the software of ChemBio3D, both the possible diastereoisomers were modelled and optimised using molecular mechanics calulations(MM2) to give a representation of the energy of each molecule. Diagrammic models of the models can bs seen right and 3D models in the links below.
Results Table
| Endo Product Energy/Kcalmol-1 | Exo Product Energy/Kcalmol-1 |
|---|---|
| 34.90 | 31.90 |
Analysis and Conclusion
As the major product (endo) is less thermodynamically stable than the minor product (exo), it can be concluded that the reaction is under kinetic control and thus as the endo rule suggests the reaction route is dictated by the relative energies of the transition states.
Dicyclopentadiene Hydrogenation
Like the cyclopentadiene dimerisation, the hydrogenation of the dicyclopentadiene can lead to the formation of two isomers, shown right.
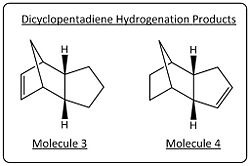
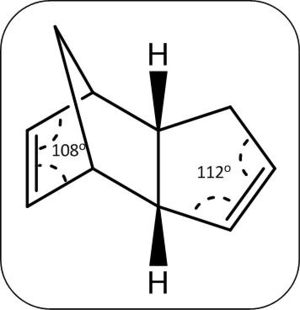
A prediction of the thermodynamically favoured product can be made by comparing the double bonds broken in each case, in the production of molecule 4, the more strained double bond on the six membered ring with the cross bridge is broken and thus predicted to be the thermodynamically favoured product.
Using the same technique the relative energies of the two products can be determined and the thermodynammic and kinetic product determined.
Modelling of Hydrogenation Products
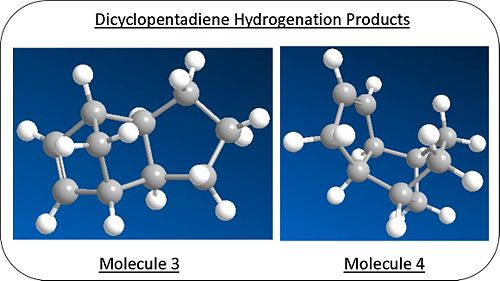
Again through the use of ChemBio3D, both the possible products were modelled and optimised using molecular mechanics calulations(MM2) to give a representation of the energy of each molecule. Diagrammic models of the models can bs seen right and 3D models in the links below.
Results Table
| Molecule 3 Energy/Kcalmol-1 | Molecule 4 Energy/Kcalmol-1 |
|---|---|
| 35.00 | 31.18 |
Analysis
As predicted the thermodynamically favourable product is molecule 4 through greater release of bond strain compared to the production of molecule 3, this can be observed through the calculated double bond angles of 108o for bond broken in the preparation molecule 4 compared to 118o for the bond broken in molecule 3 preparation (see below). The hydrogenation to molecule 3 also appears to be thermodyanamically unfavourable (through a rise in energy from the calulated dicyclopentadiene (endo 34.90 kcal/mol vs. 35.00 kcal.mol for molecule 4), an explanation for this could be the energy gain from the increase van der waals forces between the hydrogens being larger than the release of bond strain.
Full Results Table
| Molecule | Total Energy (kcalmol-1) | Bend Energy (kcalmol-1) | Torsion Energy (kcalmol-1) | Stretch Energy (kcalmol-1) | VDW Energy (kcalmol-1) | ' |
| Endo-Product | 31.90 | 20.61 | 7.63 | 1.28 | 4.24 | |
| Exo-Product | 34.90 | 20.83 | 9.51 | 1.26 | 4.31 | |
| Molecule 3 | 35.00 | 19.10 | 11.14 | 1.26 | 5.79 | |
| Molecule 4 | 31.18 | 14.52 | 12.51 | 1.10 | 4.50 |
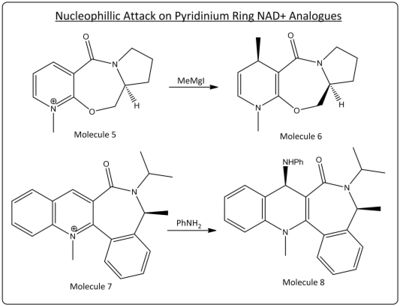
Section 1B - The Nucleophillic Attack of Pyridinium Rings
Nucleophillic attack on a pyridinium rings are very stereoselective reactions (examples seen below). Through modelling of the pyridinium ring NAD+ derviatives, seen below, using molecular mechanics the optimal geometries for the reactants can be calulated and determine the reason for this stereoselectivity.
Modelling
The reactant molecules 5 and 7 that under nucleophillic attack were modelled using the ChemBio3D software and their geometries optimised (energy minimised) using molecular mechanics (MMFF94 force field).
Molecule 5
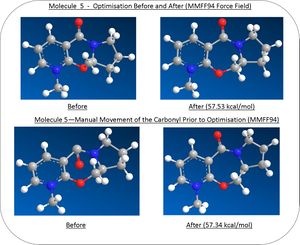
Diagrammic models of the molecules 5, before and after the geometry optimisisation calulation procedure can be seen to the left. Using the MMFF94 force field the energy of the molecule 5 was minimised to 57.53 kcal/mol. Through manual movement of the orientation of the carbonyl bond followed by further optimisation (see figure 6) , the energy was minimised to a slightly lower value of 57.34 kcal/mol - stressing the importance of the starting orientation before optimisation takes place and the possibility of a lower energy conformation.
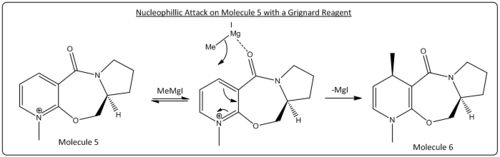
Nucleophillic Attack on Molecule 5
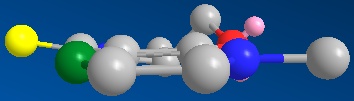
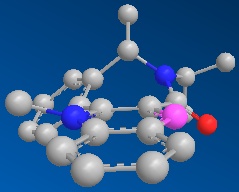
The nucleophillic attack on molecule 5 in the reaction described is through the use of a grignard reactant; MeMgI. Grignard reactants consist of both a electrophillic and nucleophillic component; the magnesium and the alkyl group respectfully. The stereoselectivity of the reaction could therefore be controlled through the interaction the electrophillic magnesium with the adjacent carbonyl to the sight of attack. Through analysis of the geometry optimised model of molecule 5 the relative orientation of the carbonyl to the planar pyridinium ring (fulfilling Huckel's rule for aromaticity) can be seen to be above the ring (in the same orientation as the methyl group added in the product)with a dihedral angle of 14.1° (see diagram below, green is site of attack and yellow carbonyl group, hydrogens removed for clarity). The magnesium coordination to the adajacent carbonyl therefore govern this high level of stereochemical control by forcing nucleophillic attack from the top (scheme below). face.
Molecule 7
Molecule 7 was modelled similarly using the ChemBio3D software and the geomerty optimised using the MMF94 force field. The optimisation minimised the energy to 113.18 kcal/mol. Through manual movement of the nitrogen (green in diagram) in the Pyridinium ring to a more planar ring position (to fulfill Huckel's aromaticity rule) prior to optimisation the energy was minimised further to 101.61 kcal/mol (as seen left). This further presses the need to trial multiple starting geometries to make sure the calulation reaches the actual minimum energy and not a local minima yielding the incorrect geometry.
Nucleophillic Attack on Molecule 7
Nucleophillic attack with Aniline on molecule 7 as describe earlier is again very stereoselective. The nucleophile aniline in this example is a large aromatic molecule with electron denisty around the phenyl ring. This electron density is likely to inccur colombic repulsion with the electron rich carbon group, thus the nucleophile will approach in a way to avoid this repulsion. Through analysis of the geometry optimised molecule 7 it can be seen that the carbonyl is orientated below the ring (opposite to the orientation of the methyl group) with a dihedral angle of - 35.8°, thus meaning attack will occur above ring creating this stereoselectivity (orientation of the carbonyl (red) with respect to the site of attack (purple) can be seen left).
Section 1C - Stereochemistry and Reactivity of an Intermediate in the Synthesis of Taxol
The anti-cancer drug of taxol have key intermediate molecules of 9 and 10 in its synthesis. Molecule 9 and 10 are examples of antropisomers, in where there is limited rotation around a single bond in the molecule, through modelling both molecules and again using molecular mechanics, the optimal geometries for both isomers can be found and relative energies compared.
Modelling
The reactant molecules 9 and 10 that under nucleophillic attack were modelled using the ChemBio3D software and their geometries optimised (energy minimised) using molecular mechanics (MM2).
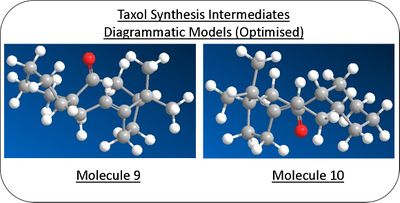
Manual changes were made to the cyclohexane ring to the lower energy chair conformation prior to optimisation to achieve the lowerest energy geometry.
| Molecule | Total Energy (kcalmol-1) | Bend Energy (kcalmol-1) | Torsion Energy (kcalmol-1) | Stretch Energy (kcalmol-1) | VDW Energy (kcalmol-1) | ' |
| Molecule 9 | 50.03 | 11.97 | 22.14 | 2.61 | 13.83 | |
| Molecule 10 | 44.34 | 10.67 | 19.60 | 2.54 | 12.55 |
Analysis
The molecular mechanics calulation yielded a relative energy of molecule 9 lower than molecule 10, thus suggesting a more stable configuration. The greater stability of the molecule 10 can be explained through the orientation of the C-H groups relative to the carbonyl group, in molecule 10 the carbonyl's sigma star (anti-bonding orbital) is orientated with the C-H groups allowing for sigma conjugation (see below) whilst in molecule 9 the orientations are not aligned and therefore no overlap.
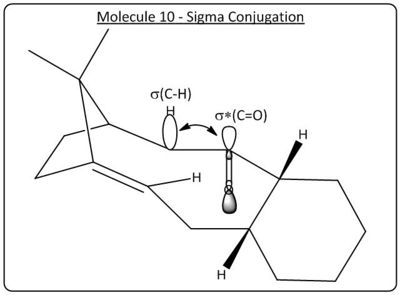
Alkene Stability
The carbon-carbon double bond seen in both intermediate molecules are members of the group known as hyper stable alkenes. As their name suggest hyper stable alkenes are very stable and thus resistant to hydrogenation or addition. By modelling the hydrogenation product of molecule 10, this stability can be explained. The molecule was modelled using ChemBio3D software and geometry optimised using the molecular mechanics method: MM2 (see right)
| Molecule | Total Energy (kcalmol-1) | Bend Energy (kcalmol-1) | Torsion Energy (kcalmol-1) | Stretch Energy (kcalmol-1) | VDW Energy (kcalmol-1) | ' |
| Molecule 10 | 44.34 | 10.67 | 19.60 | 2.54 | 12.55 | |
| Hydrogenated Molecule 10 | 58.38 | 17.23 | 22.88 | 2.92 | 15.69 |
Analysis
The stability is shown in the results achieved through the hydrogenation product having greater energy than molecule 10. This difference in energy can be explained through the strained bond angles around the hydrogenated carbons of 123° and 115°, these angles are far from the lowest energy configuration for a Sp3 carbon of 109°, resulting in the destabilisation of the molecule and higher torsional and bend energy. While the similar bond angle in molecule 10 of 124° is much close to the lowest energy angle of the a Sp2 carbon of 120° explaining the lower energy (All bond angles measured on ChemBio3D.
Hyper stable alkenes are defined by their negative olefin strain energy (strain energy before hydogenation minus after hydrogenation), as seen the hydrogenation of both molecule nine and ten gives a negative olefin strain energy and thus are hyper stable alkenes.
Section 1D - Modelling using Semi-empirical Molecular Orbital Theory
Electrophillic addition to molecule 12 (see below) is a highly regioselctive in attacking the alkene to syn to the chlorine (chlorine orientated towards the 'syn' alkene). Through modelling of molecule 12 and calulating molecular orbital wavefunctions through the MOPAC/PM6 method the orbital control of said reactions can be examined.
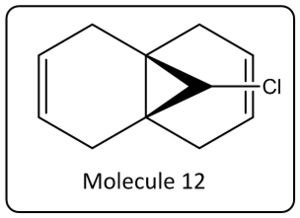
Modelling
The software of ChemBio3D was used to model molecule 12 and geometry optimised using both the molecular mechanics method MM2 (results below) and the MOPAC/PM6 algorithem (Heat of Formation = 19.74 kcal/mol). The optimisation method produced only slightly different geometries - both with a plane of symmetry perpendicular to the alkenes bonds and the carbons in the ring syn to the chlorine relatively planar to each other.
| MM2 | Total Energy (kcalmol-1) | Bend Energy (kcalmol-1) | Torsion Energy (kcalmol-1) | Stretch Energy (kcalmol-1) | VDW Energy (kcalmol-1) | ' |
| Molecule 12 | 17.90 | 4.71 | 7.69 | 0.63 | 5.80 |
Molecular Orbitals
Using the MOPAC/PM6 method, the wavefunction of the molecular orbitals can be estimated and represented graphically in ChemBio3D. A graphical representation of molecular orbitals of molecule 12 can be seen below.
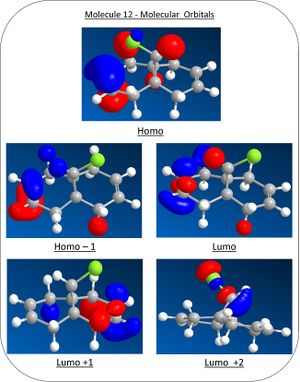
The higest occupied molecular orbitals (HOMO) can be seen to be the pi bonding orbital of the syn alkene and the HOMO-1 the pi bonding orbital on the anti alkene. The Lowest unoccupied orbital (LUMO), LUMO+1 and LUMO+ 2 are assigned to the pi antibonding orbital of the anti alkene, pi antibonding of the syn alkene and the sigma antibonding orbial of the carbon chlorine bond. This orbital arrangement explains the regioselectivity in where the HOMO is the most reactive towards nucleophillic attack and thus making attack to the syn alkene preferable.
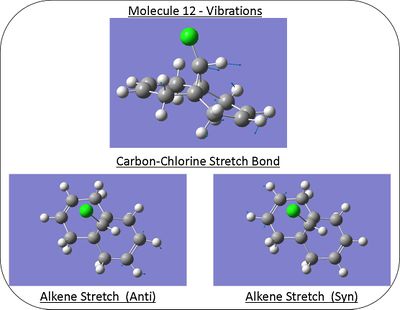
Vibrations
Using the software of Gaussian, the molecule 12 was modeled and molecular vibrations calulated, from this a infrared spectrum was estimated (link below).
Calculated Infrared Spectrum of Molecule 12
Diagrams of the molecular displacement for both alkene and carbon-chlorine stretches can be seen to the right and their repective frequencies in the table below.
| Bond | Stretching Frequency/cm-1 |
|---|---|
| Alkene (Anti) | 1737.15 |
| Alkene (Syn) | 1757.38 |
| Carbon-Chlorine | 770.86 |
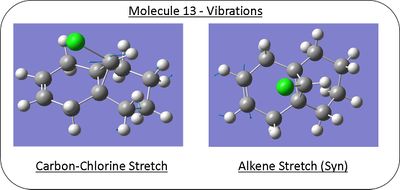
The effect of the anti alkene bond on the carbon chlorine vibration can be probed through comparison to the vibration when the alkene bond has been hydrogenated (molecule 13). Molecule 13 was modelled in a similar way using Gaussian and vibration calculated; diagrams and results are given below.
Calculated Infrared Spectrum of Molecule 13
| Bond | Stretching Frequency/cm-1 |
|---|---|
| Carbon-Carbon Bond (Anti) | 1393.00 |
| Alkene (Syn) | 1758.05 |
| Carbon-Chlorine | 774.94 |
Analysis of Vibrational Data
Comparing the vibrational wavenumber of the carbon chlorine bond in both molecules shows a increase of around 4 cm-1 through hydrogenation of the anti-alkene. It can therefore be postulated that the interaction of the alkene with the carbon chlorine bond was raising its bond length thus lowering it stretching frequency. This can be explained through conjugation of the anti-alkene pi orbital into the carbon chlorine sigma antibonding orbital, overall this lowers the energy of the molecule but destabilises the carbon chlorine bond in the process.
Anti-Alkene Bond Adjustment
To probe the suggested anti alkene pi orbital interaction with the carbon chlorine sigma anti bonding orbital; the groups adjacent to the anti alkene were changed and their effect on the vibrations recorded (see table below, vibrations calculated as before)
Comparing the vibrational wavenumber of the carbon chlorine bond in both molecules shows a increase of around 4 cm-1 through hydrogenation of the anti-alkene. As wavenumbers are proportional to energy, it can therefore be postulated that the interaction of the alkene with the carbon chlorine bond was raising its bond energy and thus length. This can be explained through conjugation of the anti-alkene pi orbital into the carbon chlorine sigma antibonding orbital, overall this lowers the energy of the molecule but destabilises the carbon chlorine bond in the process.
| Adjacent Group on Anti-Alkene | Anti C=C Stretching Frequency (cm-1) | C-Cl Stretching Frequency (cm-1) | |
| H | 1737.15 | 770.86 | |
| OH | 1797.54 | 758.81 | |
| CN | 1670.46 | 772.65 | |
| SiH3 | 1633.84 | 767.943 | |
| BH2 | 1604.49 | 761.44 |
The changes observed from changing the alkene adjacent group from hydrogens to hydroxyl and cyano groups are as expected. The electron donating nature of the hydroxyl group increasing the electron donating capacity of the alkene to the carbon chlorine antibonding orbital (increasing bind length and lowering stretching frequency). The electron withdrawing cyano group shows the expected opposie effect with a raise in carbon-chlorine stretching frequency as the group is decreasing the electron density of the alkene (decreasing donation and destabilising alkene bond itself giving a lower C=C stretch observed). The ususual results for both the BH2 (with empty P orbital) and SiH3 (with ability to expand its octet) as expected to has electron withdrawing nature however appear to have the opposite, a further look into the molecule orbitals may be shed light on this occurance. Through Gaussian optimisation the adjacent BH2 groups appear to create a cross bridge this could be the reason for this usual change to the bond frequency (structure below).
Section 2 - Structure based Mini project using DFT-based Molecular orbital methods - Domino Diels-Alder Reaction
Introduction
Domino Diels-Alder reaction are one pot processes involving two or more Diels-Alder reactions in the same reaction conditions. The Domino Diels Alder that has been modelled is shown below.
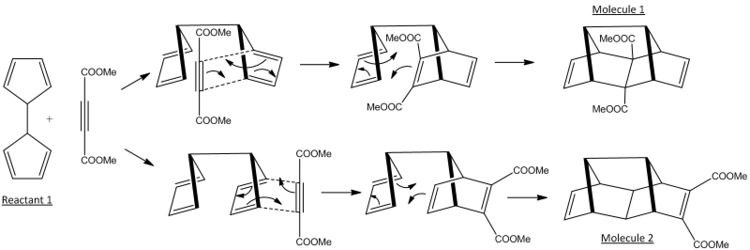
The reactions occurs through the initial diels alder reaction between one of the cyclopentadiene rings on the linked cyclopentadiene structure and the diester alkyne (dienophile) proceeded by a intramolecular diels alder reaction. Due to the two possible arrangements of the linked cyclopentadiene molecule the dieneophile can approach either 'inside' or 'outside' to the two equivilent rings producing the two regioisomers; molecules 1 and 2. The difference being the final position of the ester groups to either the end of one of the rings attached to an alkene or inbetween the rings attached to a carbon carbon single bond. The endo rule would suggest the major product would be molecule 1 as this approach seemingly yields the highest accumulation of double bonds and thus a lower energy transition state (as seen in section 1), however the Piquette Group at the University of Ohio prepared both isomers in each approximately equal amounts.
Reactant Modelling
Through modelling of the reactant diene (linked cyclopentadiene) the apparent lack of selectivity for attack can be probed. The molecule was modelled using ChemBio3D and geometry optimised through the MM2 molecular mechanics energy minimisation method and the molecular orbitals calulated with MOPAC/PM6.

The optimised structure of the reactant shows a geometry with a C2h symmetry (reactant 1D) s with an energy of 17.85 kcal/mol.
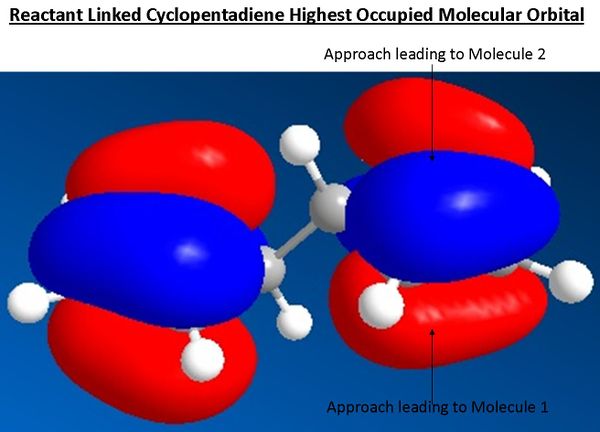
As the dieneophile in this example is a relatively electron poor alkyne with adjacent electron withdrawing ester groups the interaction of orbitals will occur with the most nucleophillic HOMO orbital. The difference between each reaction pathway is the approach of the dieneophile to either the top or bottom face of the ring; approach from top face (see diagram below) after the preceding bond rotation and second diels alder leads to molecule 2 and vice versa approach from the bottom face leads to molecule 1. As can be seen in the diagrammic picture below of the reactants HOMO orbitals there is no real difference between the orbital overlap in the approach that yields the different pathways, explaining the lack of selectivity in the reaction. Therefore the initial suggestion that the route to molecule 1 was favoured through the endo rule was incorrect and shows the importance of three dimensional visualisation and analysis.
Isomer Modelling and Identification
Seperation of the both regioisomers; molecules 1 and 2 chas been achieved through fractional distillation and identified using both proton and carbon-13 NMR. Through modelling of both isomer molecules and using Gaussian software and DFT-Based Molecular orbital method to calulate NMR spectra the difference can be observed and compared to the literature. Molecules 1 and 2 were modelled using the Gaussview Software and optimised using the DFT-MPW1PW91 method to give structures below.
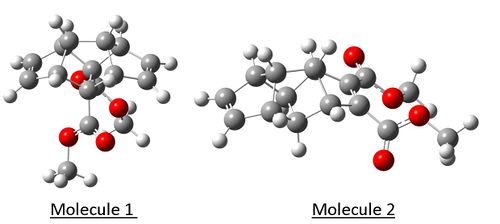
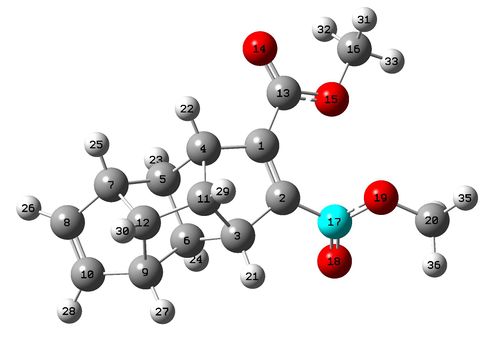
From observation of the Gaussian optimised structures above it can be seen that orientation of the ester group limits the symmetry in the molecule and thus makes many carbons and protons expected to be equivilent through initial observation inequivilent. Also observed on both molecule is the resonance bond seen between the carbonyl carbon and the ester oxygen, giving this double bond character and limiting its rotational freedom. The carbon 13 and proton NMR of both molecules can be seen below.
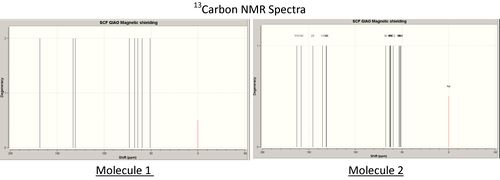
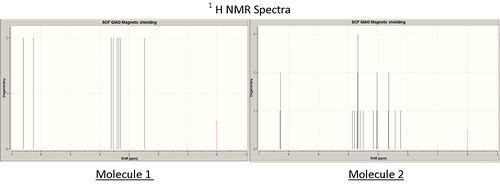
As seen above the carbon-13 and proton NMR spectra of the two isomers vary very significantly. The initial observation is that molecule 1 has more degency than the spectra of molecule 2 reflecting its greater symmetry.
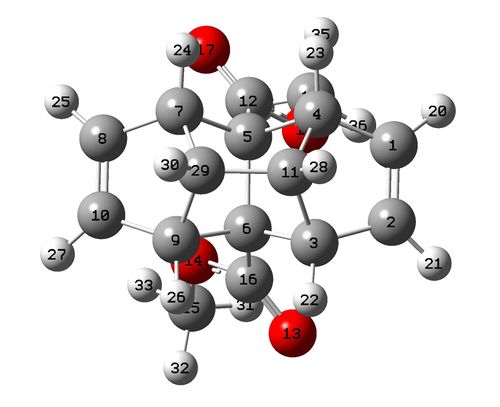
Molecule 1 NMR Data
| Literature (ppm) | Calculated (ppm) | Assignment (no.) |
|---|---|---|
| 51.5 (2C) | 51.1 (2C) | 19+15 |
| 58.8 (2C) | 59.5 (2C) | 29+11 |
| 64.4 (2C) | 64.2 (2C) | 5+6 |
| 69.5 (4C) | 67.3 (2C) 73.0 (2C) | 4+9,3+7 |
| 132.7 (4C) | 130.8 (2C) 133.9 (2C) | 2+8,10+1 |
| 172.6 (2C) | 173.97 (2C) | 16+12 |
| Literature (ppm) | Calculated (ppm) | Assignment (no.) |
|---|---|---|
| 2.48 (2H) | 2.46 (2H) | 30+28 |
| 3.28 (4H) | 3.29 (2H) 3.35 (2H) | 23+26,22,24 |
| 3.56 (6H) | 3.41 (2H) 3.53 (2H) 3.60 (2H) | 36+33,31+34,35+32 |
| 6.02 (4H) | 6.26 (2H) 6.60 (2H) | 27+20, 21+25 |
Analysis
The number of peaks observed in both the proton and carbon 13 NMR is larger than seen in the literatue, this can be explained by the rotational freedom around the bond between the carbonyl carbon and the ring (bonds 6-16 and 5-12), these bonds can rotate so that the orientation of the ester groups can switch to their counterparts orientation similtantiously. In a measure NMR spectrum a time average spectrum is achieved (as measurement slower than this rotation motion) thus creating more degeneracy, however the NMR calculated for this model was of a single orientation thus peaks are not averaged creating the observed greater number of peaks. However the peak positions and assignments shows good correlation in both proton and Carbon-13 NMR to the literature.
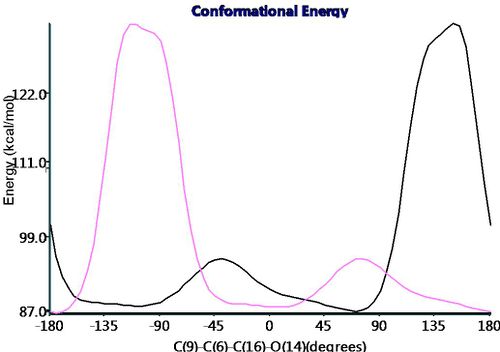
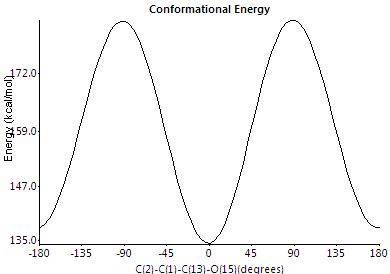
This apparent free rotation around the carbonyl-ring bonds was be probed through rotating around the bonds and measuring the change in conformation energy using the dihedral driver function on ChemBio3D. The below graph shows the change in conformation energy when rotating the bonds (pink and black lines for opposite ester groups). As can be seen there are two minima regions that either esters can be orientated in and switch between and thus if this rotation is faster than the time scale of NMR the shifts observed would be for a average configuration. The barrier to rotation is unsymmetry in terms of direction of rotation suggest restricted rotation due to sterical bulk surroundings. To probe further into this free rotational averaging of the NMR shifts, both ester group could be rotating at the same time to see how simultanous rotations effect the energy of the molecule.
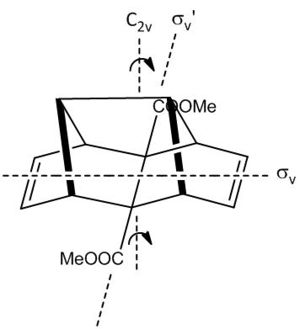
Therefore assuming a average orientation for both ester groups (in the time scale of NMR) this will cause the molecule to appear to have that of C2v symmetry as shown right.
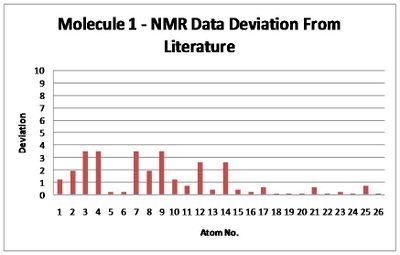
Despite this time averaging difference between the literature NMR and that calulation, as can be seen in the graph below (plotting the deviation from the literature NMR ppm values), the calulated spectra value do not show much significant variation and within the expected accuracy of 5ppm, thus accurately calculated.
Molecule 2 NMR Data
| Literature (ppm) | Calculated (ppm) | Assignment (no.) |
|---|---|---|
| 49.4 (2C) | 50.3 (2C) | 20+16 |
| 51.8 (2C) | 52.7 (1C) 53.2 (1C) | 5,6 |
| 60.7 (2C) | 59.6 (1C) 63.0 (1C) | 11,12 |
| 61.2 (2C) | 62.3 (1C) 62.5 (1C) | 7,9 |
| 62.4 (2C) | 63.3 (1C) 67.4 (1C) | 4,3 |
| 132.2 (2C) | 131.1 (1C) 131.3 (1C) | 10,8 |
| 140.4 (2C) | 135.1 (1C) 145.9 (1C) | 1,2 |
| 165.2 (2C) | 168.6 (1C) 164.1 (1C) | 17,13 |
| Literature (ppm) | Calculated (ppm) | Assignment (no.) |
|---|---|---|
| 2.13 (2H) | 2.24 (1H) 2.46 (1H) | 23+24 |
| 2.58 (2H) | 2.62 (2H) | 29+30 |
| 2.97 (2H) | 3.02 (2H) | 25+27 |
| 3.25 (2H) | 3.16 (2H) | 21+22 |
| 3.72 (6H) | 3.59 (1H) 3.67 (3H) 3.78 (1H) 3.86 (1H) | 33,35+31+34,32,36 |
| 5.83 (2H) | 6.27 (2H) | 28+26 |
Analysis
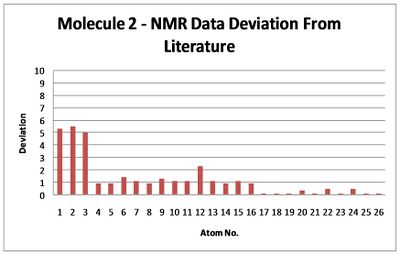
Similarly to molecule 1, the number of peaks in the NMR spectra is larger for calulated spectra than that reported in the literature. This can be explained as before in where due to the rotation freedom around the ring-carbonyl bond (17-2,13-1) that mean the interconversion of the two ester orientations can occur in the time scale of NMR measurement. The single orientation used in the calculation however does show larger deviation from the literature than molecule 1, a possible explanation is the larger rotational freedom around the carbonyl-ring bond as attached to an Sp2 carbon with a bond angle of 131.8° from the ring together with less steric bulk surrounding it and thus more possible stable configuration (literature NMR average over larger range of structural geometries), whilst in molecule 1 the similar bond is attached to a strained Sp3 carbon with a bond angle of 115.9° together with the steric bulk from the surrounding ring restricting its rotational freedom. The conformation energy change with rotation is symmetric suggesting no sterical obstruction in either direction.
With the averaging of the ester group geometry the molecule will appear with Cs symmetry with only a sigma-h reflection plane perpendicular to the alkene bonds. The NMRs show significant difference between the molecules due to the difference in molecular symmetry and positioning of the ester group relative to the rest of the molecule making NMR a resonable technique for identification of the two isomers.
Infrared Spectroscopy
The difference between the point of attachment of the ester groups could also be seen in vibration measurements as in molecule 1 the esters are attached to a single bonded carbon whilst in molecule 2 the ester groups are attached to the alkene group. This attachment to the alkene of the electron withdrawing ester group will effect the observed C=C stretch in the infrared spectra and thus can be used as a identification tool to distinguish between the two isomers. The infrared spectra was calculated using the Gaussian software and the DFT-MPW1PW91 method to give the spectra below.
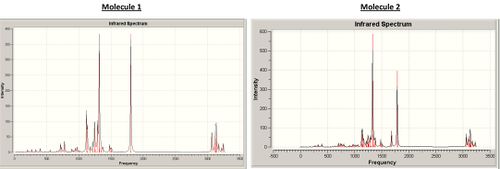
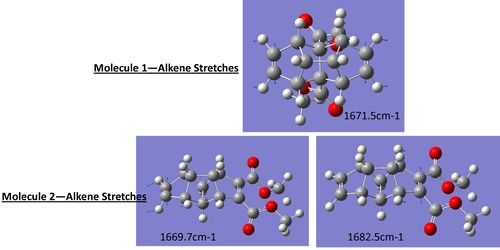
As expected the obvious difference in the infrared spectra is the alkene stretch, molecule 1 shows a single stretch for both equivilent alkene stretching at the same time at 1671.5cm-1 whilst molecule 2 shows two alkene stretches, one for the alkene group with adjacent esters at 1682.5cm-1 and one for the opposite alkene at 1669.93cm-1. This difference is again due to the differences in symmetry of the molecule (below are diagrams for the stretches observed in the two molecules). As can be seen in the data below with the common error of 5% in these calulations the stretches match well to the literature values and is another good techniques in distinguishing between the two isomers.
| Molecule | Calulated Stretching Frequency (cm-1) | Assignment | Literature |
|---|---|---|---|
| Molecule 1 | 1672 | C=C Stretch | 1727 |
| Molecule 2 | 1670 | C=C Stretch | 1631 |
| Molecule 2 | 1683 | C=C Stretch (esters attached) | 1720 |
The calulated free energies of both molecules reflects further this lack of stereoselectivity with both molecule having very similar energies of 3.8x105kcal/mol, thus a lack of thermodynamic selectivity as well no kinetic selectivity through the endo rule (concluded before) therefore leading to equal chance of either reaction pathway.
Conclusion
Using molecular modelling the reaction was probed with success to determine explanation for the lack of selectivity in the reaction. The calculated NMR showed relatively good correlation with the literature with only explainable errors as did the IR spectral data and enabled identification between the two isomers easierly. A expansion to this project would be to probe this free rotation around the bond using different adjacent groups and thus determine whether as suggested steric bulks and bond angle alter this in a significant way.
References
Exercise 2 A. G. Shultz, L. Flood and J. P. Springer, J. Org. Chemistry, 1986, 51, 838.
Exercise 3 S. Leleu, C.; Papamicael, F. Marsais, G. Dupas, V.; Levacher, Vincent. Tetrahedron: Asymmetry, 2004, 15, 3919-3928. Alan B. McEwent and Paul von Rague Schleyer, J. Am. Chem. Soc., 1986, 108, 3951-3960.
Exercise 4 B. Halton, R. Boese and H. S. Rzepa., J. Chem. Soc., Perkin Trans 2, 1992, 447
Miniproject
Main Journal, http://pubs.acs.org/doi/abs/10.1021/ja00486a042 (refered to as literature above)
Henry Rzepa, Pericyclic Reactions Problems, http://www.ch.ic.ac.uk/rzepa/
Francesco Fringuelli, Aldo Taticchi, The Diels-Alder reaction: selected practical methods, Wiley, West Sussex, 2002
