Yw21218 MRD

H + H₂ System

Dynamics from the transition state region

Definition of transition state

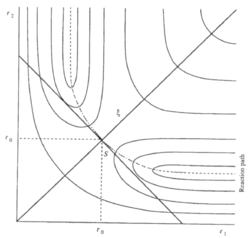
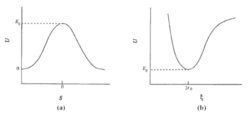
According to Chemical Kinetics and Dynamics, the transition state is a special minimum The transition state is not a minimum, and it is also not a local minimum. Fdp18 (talk) 12:40, 16 May 2020 (BST) . It has the maximum energy of the minimum energy path, hence it is also called saddle point. This is its special characteristics to separate it from other local minima. In a symmetrical potential energy surface (where reactants have the same energy as the products), the saddle point is at the intercept of S and ξ as shown in Figure 1. S = r₂ + r₁ and ξ = r₂ - r₁. The cross sections by cutting the surface energy plot along S and ξ are shown in figure1.a and 1.b respectively, where E₀ is the energy of the transition state. Mathematically, it is the solution of the following equations: $\frac{{\partial }^{2}U}{\partial s}=0$, $\frac{dU}{ds}<0$ , $\frac{{\partial }^{2}U}{\partial \xi }=0$ , $\frac{dU}{d\xi }>0$

The redefinition of coordinate systems you use here is sensible. However, the equations are erroneous. Think back to curve sketching: what does the second derivative mean? What the first? I would also recommend you to look up again what a 'stationary point' is, and how you can use first and second derivatives to decide what type of local extremum you have. See also 'Hessian'. Fdp18 (talk) 12:46, 16 May 2020 (BST)

Figure 1. Saddle point region of symmetrical potential energy surface

Figure 1.a, 1.b. Cross Sections of potential energy surface

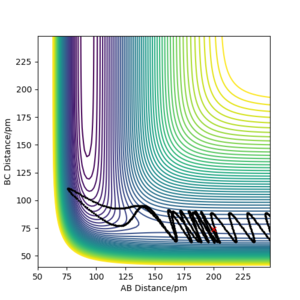
Location of transition state

Figure 2. H-H-H system

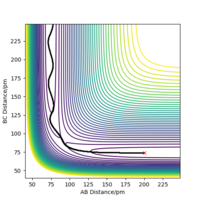
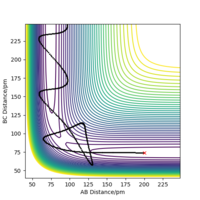
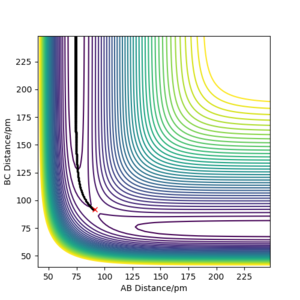
Because the potential energy surface is symmetrical, initial condition can be set as r₁ = r₂. To eliminate the effect of external forces and the bond oscillation, p1 = 0 g.mol^-1.pm.fs^-1, p2 = 0 g.mol^-1.pm.fs^-1, and MEP calculation should be used. A decent guess can start from the saddle point region discussed above. The ideal transition state position is found when the trajectory is just a dot in the contour plot, even with step number is as large as 5000 (if the initial condition is at transition state, no reaction should occur over the time). Another way to confirm the transition state position is to check if the calculated forces are close to zero, because force is the negative derivative of the potential energy. Finally, r_ts = r₁ = r₂ = 91 pm, with potential energy of -415.369 KJ mol^-1. The reactant potential energy is -434.705 KJ mol^-1, hence the activation energy is the energy difference 19.336 KJ mol^-1.

At this point, r_AB and r_BC are equal and constant, which has been proven by the 'Internuclear distance vs Time' plot (Figure 3).

figure 3. 'Internuclear distance vs Time' plot.(The atom notations can be found in Figure 2)

Transition state is at the point where slope equals to zero, without any external forces it doesn't have preference to form products or reactants, hence the atoms are still relative to each other.

MEP and trajectory

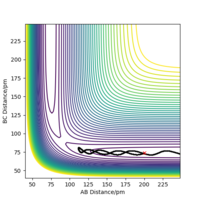
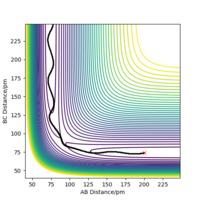
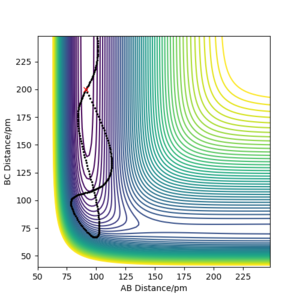
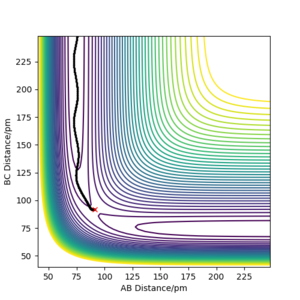
Minimum energy path is in theory the trajectory that reaction should follow, corresponding to the lowest energy valley of the potential energy surface. MEP calculation sets the momenta to zero at every step in the trajectory, therefore, it doesn't take into account the vibrational energy of molecules. However, 'Dynamics' calculation can generate a more realistic trajectory by keeping the momenta as what they are in the previous step, so it shows the bond oscillation. To compare those two calculations, their corresponding trajectories were produced under the same initial conditions: r₁ = r_ts+ 1 remember to always use units - if you don't, one will assume that you use atomic units, which is clearly not the case. And even with atomic units there are different sets in use. Fdp18 (talk) 12:49, 16 May 2020 (BST) , r₂ = r_ts, p1 = p2 = 0 g.mol^-1.pm.fs^-1, and are shown in Figure 4.1 and Figure 4.2. The dynamics calculation gives a wavy trajectory, indication the bond vibration after overcome the energy barrier. The extra kinetic energy is from the energy difference between the transition state and the reactant.

Figure 4.1. MEP calculation trajectory

Figure 4.2. Dynamics calculation trajectory

Reactive and unreactive trajactory

Identifying reactive trajectories

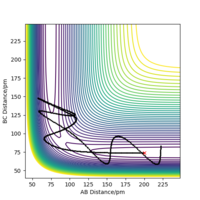
The amplitude of the trajectory waves indicates the amount of vibrational energy. The greater amplitude the waves have, the more vibrational energy the system has at that stage.

When the kinetic energy (KE) is lower than the activation energy (E_a), the reaction will not complete. Is this statement rigorously valid? Think about potential energy. If you start at or even above the transition state, then you will have more than enough energy to overcome the activation barrier, even if you start with zero KE. Fdp18 (talk) 12:51, 16 May 2020 (BST)

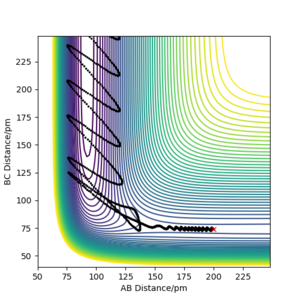
When KE reaches the Ea, the extra energy will become vibrational energy to the molecules. However, if the vibrational energy is too high, it can cause the reaction reform the reactants even if the collision occurs and energy barrier is overcame. With high kinetic energy, energy barrier is no longer the factor to determine the reaction reactivity. 

Table 1. Reactive and unreactive trajectories

P1 / g.mol-1.pm.fs-1	P2 / g.mol-1.pm.fs-1	Etot / KJ mol-1	Reactive?	Description of the dynamics	Illustration of the trajectory
-2.56	-5.1	-414.280	yes	The molecule H2 has small vibrations before reaching the transition state and the vibration amplifies slightly after it overcomes the energy barrier and forms product
-3.1	-4.1	-420.077	no	The kinetic energy 13.710 KJ mol-1 input in the reaction is less than the activation energy, so it cannot overcome the energy barrier to form products. The reactants have a certain amount of vibrational energy when reaction starts and it is the same amount at the end.
-3.1	-5.1	-413.977	yes	The kinetic energy in the system is slightly higher than that in the first example, so the amplitude of the waves of the trajectory is greater, indicating more energy used to vibrate. Hence the product has a greater oscillation.
-5.1	-10.1	-357.277	no	The kinetic energy is nearly four times as much as the activation energy. It overcomes the energy barrier and the vibration is significant, but due to vibrational motion, it reforms the reactants at the end. Because when kinetic energy is too high, energy barrier is not playing in a role in achieving reactive path, instead, it depends more on the trajectory with the given initial conditions.
-5.1	-10.6	-349.477	Yes	Although in this case the kinetic energy is quite large, it does manage to reach the product after some chaos around saddle point region. In this case, the trajectory has managed to reach the products.

Transition state theory and experimental data

It is assumed in Transition State Theory (TST) that once the molecular system has crossed the transition state, it can not go back to the reactants. However, it is not always the case in experiments. In the second last case mentioned in the table above, the kinetic energy should be high enough to overcome the energy barrier, it is expected that the reaction should go to completion according to TST. However, the more realistic trajectory based on dynamics calculation shows it should bounce back from the energy surface and reform the reactants at the end. With high kinetic energy, energy barrier is no longer the key to have a reactive path. It depends more on how vibrational and translational motion interact with the energy surface to form a trajectory.

Besides, TST simplifies the motion of molecules to one dimensional motion in reaction coordinate and separates molecular motion into electronic and nuclear part. The last part is the born-oppenheimer approximation, not directly the TST. Fdp18 (talk) 12:56, 16 May 2020 (BST)

In reality, molecules also have other normal reaction motions like vibration. Hence, the reaction trajectory may be above the minimum energy configuration on the potential energy surface, hence may require higher activation energy than the energy barrier. 

Another limitation of the TST is that it can predict reasonably accurate saddle point via harmonic potential at low temperature, but when the temperature is high the potential harmonic requires some anharmonic correction.

F-H-H System

PES inspection

classification of the reactions

Figure 5. F-H-H system

Figure 6. Energy surface plot of FHH system

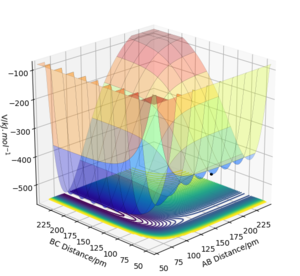
As shown in Figure 6, at small BC distance F + H₂ is on the right, while HF + H is on the left at small AB distance. The energy graph indicates F + H₂ is going to have exothermic reaction, but FH + H system will undergo an endothermic reaction. It is consistent with the bond strength of HF and H₂. 𝛥H_HF = 181.5 JK mol^-1, 𝛥H_H2 = 74.5 JK mol^-1. Bond breaking is endothermic and bond making is exothermic. By looking at the reaction HF + H → F + H₂, the enthalpy is 107 JK mol^-1, indicating it is endothermic reaction, and vice versa.

Since you have given no references here (as you did correctly in the other parts of this report), I assume that you calculated the values for bond strength etc yourself. How did you do this? Fdp18 (talk) 12:58, 16 May 2020 (BST)

Transition state and activation energy

As mentioned in H-H-H system, calculation is set as MEP, p1 = p2 = 0 g.mol^-1.pm.fs^-1, step number = 5000. However, the energy surface is not symmetrical, so r1 is not equal to r2. According to Hammond Postulate, the transition state is more similar to the reactant in exothermic reaction and it is similar to the product in endothermic reaction. Therefore, the transition state in FHH system should be closer to H₂ + F side.

Starting with the condition r_HH = 94 pm, r_FH = 200 pm. After running the guessed position with MEP calculation, if the trajectory goes towards FH +H, we should increase the F-H distance, if it goes towards H₂, we should decreases F-H distance. Adjust those two parameters until the trajectory is only a dot at the starting position. After several attempts, the transition state is located at r_HH = 94 pm, r_FH = 181.35 pm, with potential energy at -433.942 KJ mol^-1.

Well explained what you did here. Fdp18 (talk) 13:04, 16 May 2020 (BST)

To find the activation energy of the reaction, the difference of the potential energy of reactants and transition state is what we are looking for (still keep momenta as zero, so no kinetic energy). Based on the settings of the transition state, one can increase the FH distance to find the most stable position for H + H₂, hence its potential energy. The energy of FH + H can be found by decreasing the FH distance and locate the last position.

H + H₂ potential energy is -434.536 KJ mol^-1 at r_FH = 230 pm and r_HH = 74 pm, so E_a = 0.594 KJ mol^-1

HF + H potential energy is -560.417 KJ mol^-1 at r_FH = 92 pm and r_HH = 262 pm, so E_a = 126.475 KJ mol^-1

Reaction dynamics

Mechanism of release of the reaction energy

Figure 7. a F + H₂ system, r_FH = 200pm r_HH = 74pm, p_FH = -1 g.mol^-1.pm.fs^-1 r_HH = -0 g.mol^-1.pm.fs^-1

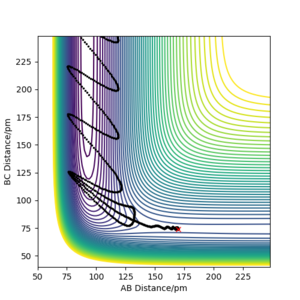
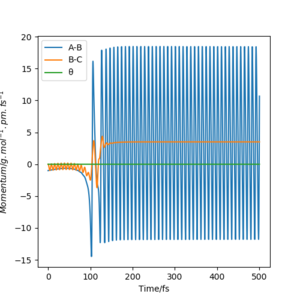
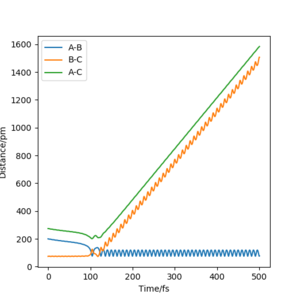
As seen in figure 7, there is little vibrational energy in when the reaction starts. After overcome the energy barrier, trajectory goes down the hill and form products. Since the potential energy of the products is a lot less than the reactant, so the extra energy is converted to vibrational energy. This is why we can see an amplified waves in product region. The momenta vs time diagram shows the small vibrations of HH bond at the beginning of the reaction, and nearly no vibrations between F and H. As reaction goes along the reaction coordination, the vibrational energy is transferred to the FH bond with a greater amount. The internuclear distance vs time diagram indicates the same result of the vibration migration and the increase of vibrational energy in product. In the energy vs time diagram, it confirms that the kinetic energy has increased after reaction goes to the products and the total energy is conservative.

To measure kinetic energy, calorimeter can be used, because higher kinetic energy will lead to higher temperature. To measure the vibrational energy, IR spectrometer can be used to measure the emission or the absorption of transition. Because the population at a specific vibrational energy level is proportional to the transition energy absorbed or emitted, and the vibrational frequency can indicate the type of bond, we can therefore find out the vibrational energy of the bond of interest. The absorption of energy to transmit the from ground energy level is greater than that of the transition from the first energy level to the second. Besides, the population at ground level is much more than that in first energy level. Therefore, transition (0→1) gives a much more intense peak at higher energy in IR spectrum, where the intensity of the peak absorption can be used to calculate the amount of vibrational energy. Experimentally, stop flow can be used to collect IR spectra frequently as the reaction is happening, which can monitor the changes of vibrational energy of the reaction.

This reaction might be a bit challenging to realise in stopped flow, but technically yes. Fdp18 (talk) 13:06, 16 May 2020 (BST)

Figure 7.1 reactive F + H2 system, momenta vs time

Figure 7.2 reactive F + H2 system, energy vs time

Figure 7.3 reactive F + H2 system, internuclear distance vs time

Distribution of kinetic energy between translation and vibration

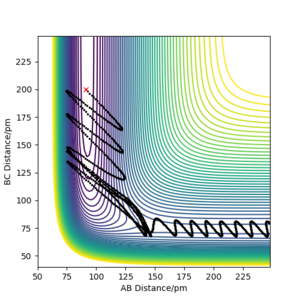
According to Polanyi's empirical rules, vibrational energy is more efficient in promoting later barrier reaction (endothermic reaction) than translational energy, while for early barrier reaction (exothermic reaction) translational energy is more efficient. To illustrate the rules, several trajectories with different initial settings were plotted. Kinetic energy is the sum of the translational and vibrational energy, so if one is small, the other must be dominant. Starting from the reactant position of A + BC, the momentum on the bond of the reactant molecule BC reflects the vibrational energy, while the momentum between the single atom A and the middle atom B can reflect the translational energy. The relative amount of those two energies can play roles in the completion of the reaction. As shown in the table below, with similar amount of kinetic energy, FH + H system prefers vibrational energy to complete the reaction. With low translational energy, sufficient vibrational energy can lead to a reactive path. However, as the kinetic energy increases, higher translational energy doesn't necessarily ensure a successful reaction if the vibrational energy is not sufficient. On the other hand, H + H₂ prefers translational energy in a reactive path. Too much vibrational energy cannot help the reaction much to go towards the transition state, and sometimes may even make the trajectory bounce back to reactants after overcome the energy barrier.

I'm missing some references here - the rest is ok. Fdp18 (talk) 13:08, 16 May 2020 (BST)

	HF +H (exothermic)	H2 + H (endothermic)
Translational E > Vibrational E	rFH = 91pm rHH = 200pm, pFH = -2 g.mol-1.pm.fs-1 rHH = -15 g.mol-1.pm.fs-1	rFH = 200pm rHH = 74pm, pFH = -1 g.mol-1.pm.fs-1 rHH = -6 g.mol-1.pm.fs-1
Translational E <Vibrational E	rFH = 91pm rHH = 200pm, pFH = 14 g.mol-1.pm.fs-1 rHH = -2 g.mol-1.pm.fs-1	rFH = 200pm rHH = 74pm, pFH = -1 g.mol-1.pm.fs-1 rHH = 0 g.mol-1.pm.fs-1