Y2COMP:bd316
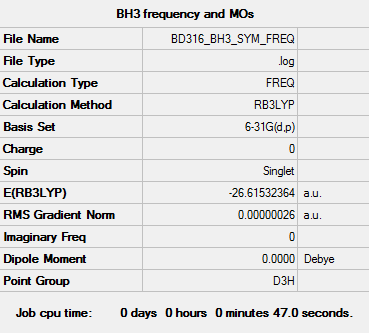
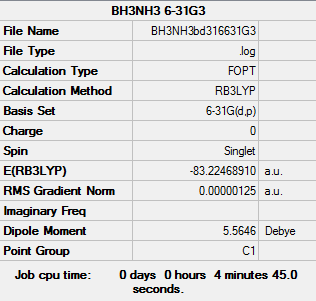
BH3
Basis set - 6-31G
Computational level - B3LYP
The results of the optimisation are as follows:
Item Value Threshold Converged? Maximum Force 0.000001 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000002 0.001800 YES RMS Displacement 0.000001 0.001200 YES
BH3 |
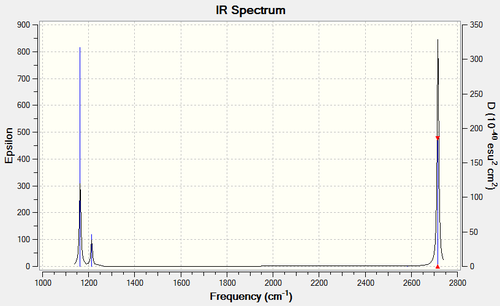
The results of the frequency analysis are as follows:
Low frequencies --- -9.0337 -9.0167 -0.0526 0.0009 0.5551 3.5044 Low frequencies --- 1162.9922 1213.1509 1213.1511
The frequencies of the vibrational modes
BH3 has point group D3h.
| Frequency (cm-1) | Intensity (arbitrary units) | Symmetry | IR active? | Type |
| 1163 | 93 | A2" | yes | symmetric bend |
| 1213 | 14 | E' | very slight | asymmetric bend |
| 1213 | 14 | E' | very slight | symmetric bend |
| 2583 | 0 | A1' | no | symmetric stretch |
| 2716 | 126 | E' | yes | asymmetric stretch |
| 2716 | 126 | E' | yes | asymmetric stretch |
The IR spectrum:
In the spectrum, only three of the six vibrations are visible. This is because, firstly, one of the vibrations, that corresponding to the symmetric stretch at 2583 cm-1, is IR-silent. This because it is totally symmetric and hence does not result in a change in dipole moment. Secondly, there are two sets of two degenerate vibrations, the peaks for which occur at the same frequency and hence are indistinguishable.
Smf115 (talk) 01:14, 17 May 2018 (BST)Well written and thorough explaination of the number of peaks seen in the spectrum and correctly assigned modes.
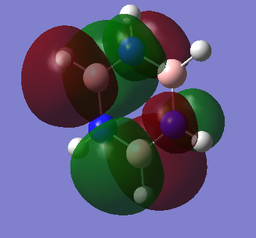
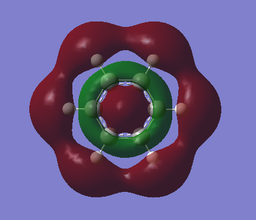
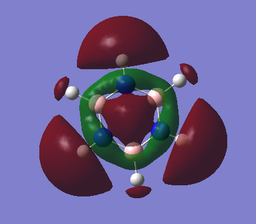
The MOs of BH3
The computed MO4 appears to show a lesser contribution from the 2S B atomic orbital than from the H3 fragment orbital, unlike the qualitative LCAO molecular orbital which predicts a greater relative contribution from the B 2S atomic orbital. It is difficult to qualitatively predict with accuracy the relative energies of the various orbitals; this discrepancy suggests that in fact the H3 fragment orbital is higher in energy than the boron 2S atomic orbital.
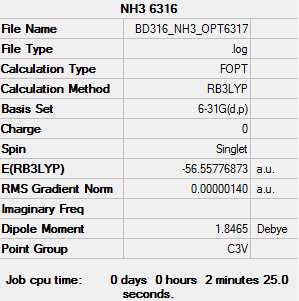
NH3
Basis set - 6-31G
Computational level - B3LYP
The results of the optimisation are as follows:
Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000002 0.000010 YES Maximum Displacement 0.000029 0.000060 YES RMS Displacement 0.000017 0.000040 YES Predicted change in Energy=-1.087432D-10
NH3 |
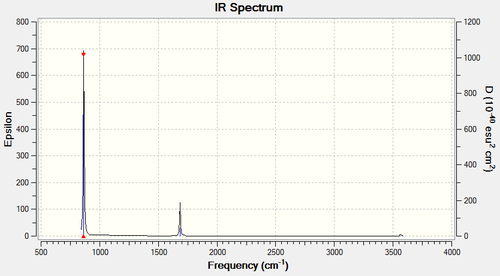
The results of the frequency are as follows:
Low frequencies --- -7.9447 -5.4530 -5.4526 0.0008 0.0035 0.0116 Low frequencies --- 1089.4132 1693.9304 1693.9304
File:BD316 NH3 OPT631 FREQ4.LOG
The frequencies of vibrational modes
| Frequency (cm-1) | Intensity (arbitrary units) | Symmetry | IR active? | Type |
| 1089 | 145 | A1 | yes | symmetric bend |
| 1694 | 14 | E | very slight | asymmetric bend |
| 1694 | 14 | E | very slight | symmetric bend |
| 3461 | 1 | A1 | very slight | symmetric stretch |
| 3590 | 0 | E | no | asymmetric stretch |
| 3590 | 0 | E | no | asymmetric stretch |
BH3NH3
Basis set - 6-31G
Computational level - B3LYP
Item Value Threshold Converged? Maximum Force 0.000002 0.000015 YES RMS Force 0.000001 0.000010 YES Maximum Displacement 0.000027 0.000060 YES RMS Displacement 0.000010 0.000040 YES Predicted change in Energy=-9.107835D-11
BH3NH3 |
The results of the frequency analysis are as follows:
Low frequencies --- -1.8806 0.0004 0.0007 0.0008 5.8284 6.3699 Low frequencies --- 263.3965 632.9709 638.5079
Ammonia-borane association energies
E(NH3) = -56.5578 a.u. E(BH3) = -26.6153 a.u. E(H3NBH3) = -83.2247 a.u.
ΔE = (E(NH3) + E(BH3)) - E(H3NBH3)
Dissociation energy = 0.0516 a.u. = 129 kJ mol-1
The bond dissociation energy of the CC bond in H3 is 618.3 +- 15.4 kJ mol-1.1 The NB bond is significantly weaker than this, which is perhaps indicative of the weaker interaction of the orbitals which form the BN bonds, due to the difference in energy between the boron and nitrogen orbitals and the worse overlap due to the difference in size.
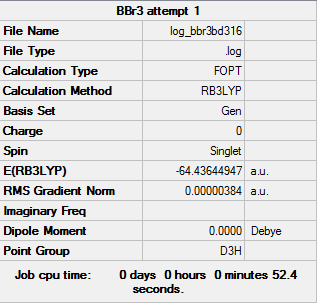
BBr3
Basis set - Gen
Computational level - RB3LYP
The results of the optimisation are as follows:
Item Value Threshold Converged? Maximum Force 0.000008 0.000450 YES RMS Force 0.000005 0.000300 YES Maximum Displacement 0.000036 0.001800 YES RMS Displacement 0.000024 0.001200 YES Predicted change in Energy=-4.086094D-10
BH3 |
Frequency analysis:
Project : aromaticity of benzene and borazine
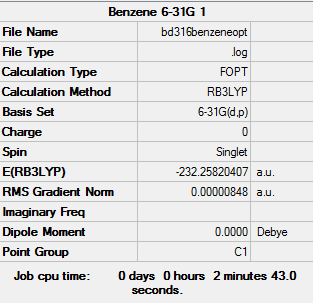
Benzene
Basis set - 6-31G Computational level - B3LYP
Item Value Threshold Converged? Maximum Force 0.000013 0.000015 YES RMS Force 0.000004 0.000010 YES Maximum Displacement 0.000054 0.000060 YES RMS Displacement 0.000017 0.000040 YES Predicted change in Energy=-1.965796D-09
Benzene |
The results of a frequency analysis on the optimised structure of benzene are as follows:
Low frequencies --- -3.9416 -0.0010 0.0003 0.0005 5.4503 7.6074 Low frequencies --- 414.5266 414.5883 621.0905
Borazine
Basis set - 6-31G
Computational level - B3LYP
Item Value Threshold Converged? Maximum Force 0.000009 0.000015 YES RMS Force 0.000003 0.000010 YES Maximum Displacement 0.000027 0.000060 YES RMS Displacement 0.000008 0.000040 YES Predicted change in Energy=-4.809258D-10
Borazine |
The results of a frequency analysis on the optimised structure of borazine are as follows:
Low frequencies --- -7.2362 -0.0005 0.0000 0.0009 4.3039 7.4691 Low frequencies --- 289.5823 289.7102 404.4530
File:BD316BORAZINEEXPTFREQ.LOG
Comparison and analysis
Charge analysis
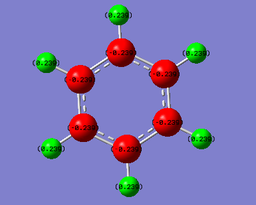
The following table shows the results of an NBO charge analysis on the benzene and borazine:
| Benzene | Borazine | ||||
|---|---|---|---|---|---|
 |
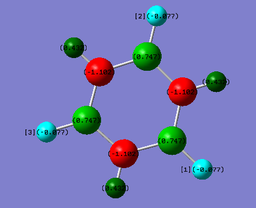
| ||||
| NBO charges | |||||
| H atoms: 0.239 | H(-B) atoms: -0.077; H(-N) atoms : +0.432 | ||||
| C atoms: -0.239 | N atoms: -1.102; B atoms: 0.747 | ||||
NBO charges demonstrate the distribution of charge in the molecule. This is determined by the relative electronegativities of the various substituents - the tendencies of the atoms to attract the electron density within the molecular orbitals.
In benzene, the carbon atoms, with an electronegativity of 2.55, are electron-rich, whereas the H atoms, with an electronegativity value of 2.20, are electron-deficient. This is because the electron density localised between the C and H atoms is attracted more strongly by the carbon atoms. This effect is more pronounced between the N and H atoms in borazine, because nitrogen is more electronegative than carbon. The boron atoms in borazine are electron-deficient relative to the hydrogen atoms to which they are attached, because boron is more electropositive than hydrogen, with an electronegativity value of 2.04.
Smf115 (talk) 01:07, 17 May 2018 (BST)Great mention of the electronegativities. Considering other points such as symmetry and the neutral charge overall would be an improvement, alongisde the correct colour range for the charge districution across both molecules.
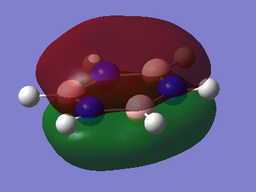
Molecular orbital analysis
Below is a comparison of three selected comparable molecular orbitals of benzene and borazine. For the purposes of analsysis the axis system is defined as:
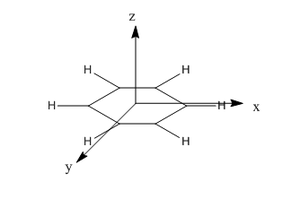
Smf115 (talk) 01:06, 17 May 2018 (BST)Great comparison of the MOs and nice extra information with the LCAOs (although check the phases of the LUMO LCAO!)
Aromaticity
An aromatic compound displays unusual or 'special' stability relative to the comparable conjugated linear molecule. For example, the aromatic stabilisation energy of benzene has been reported as 152 kJ mol-1.2 All aromatic compounds are planar, cyclic and display bond lengths intermediate between that of the expected length of the single bond and that of the expected length of the double bond.3 However, these criteria are not fully sufficient as a predictor for aromaticity.
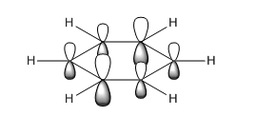
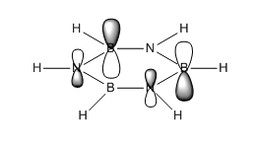
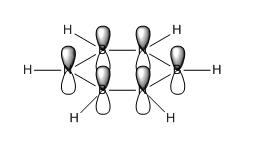
Both benzene and borazine are aromatic. In benzene each carbon atom contributes one electron to the delocalised aromatic pi system (the fully-bonding orbital for which is MO17 above); in borazine, each N Pz orbital contributes two electrons to this and the B Pz orbitals are empty but accept electron density. The lowest energy fully-bonding molecular orbital for this aromatic system is MO17 above. The presence of these conjugated Pz orbitals is not necessarily a reliable predictor of aromatic character, as it was considered to be in some of the earliest concepts of aromaticity.3 Some molecules may even be cyclic, planar, have a contiguous array of pi electrons and be 'anti-aromatic', displaying special instability relative to the linear analogue (although said systems will often contort to adopt non-planar geometries to avoid the anti-aromaticity).
Benzene and borazine demonstrate Hückel aromaticity, in that they have (4n+2) pi electrons. Cyclic planar systems are anti-aromatic by Hückel's criteria if they have (4n) pi electrons.4 Hückel et. al. developed his quantum mechanical description of aromaticity in the 1930s, as a refinement on the concepts of aromaticity developed by Kekule, Erlenmeyer and others in the late 19th century.3,4
Smf115 (talk) 01:04, 17 May 2018 (BST)A good, well referenced answer. A further development on MO 17 being just one MO which contributes to the delocalisation of the electron density in the molecule would have been good. The use of MO 17 as a reference was really good though, tieing in the molecules just studied.
Smf115 (talk) 01:15, 17 May 2018 (BST)Overall a very good report with a few mistakes made but very good MO analysis in the second section.
References
1 - https://notendur.hi.is/agust/rannsoknir/papers/2010-91-CRC-BDEs-Tables.pdf
2 - https://pubs.acs.org/doi/abs/10.1021/ja001274p
3 - https://onlinelibrary.wiley.com/doi/epdf/10.1002/chem.200700250
4 - https://link.springer.com/content/pdf/bfm%3A978-90-481-3560-8%2F1.pdf