Vg3217 inorg2ndyear

Part I

BH₃ optimisation

Method: B3YLP

Basis set: 6-31G (d,p)

Gaussview summary table of an optimised BH₃ molecule

         Item               Value     Threshold  Converged?
 Maximum Force            0.000011     0.000450     YES
 RMS     Force            0.000007     0.000300     YES
 Maximum Displacement     0.000043     0.001800     YES
 RMS     Displacement     0.000028     0.001200     YES
 Predicted change in Energy=-6.942915D-10
 Optimization completed.
    -- Stationary point found.

Frequency calculation log file

Low frequencies ---  -14.6858  -14.6818  -11.0436    0.0010    0.0165    0.3415
Low frequencies --- 1162.9492 1213.1220 1213.1222

Optimised BH3 molecule

wavenumber (cm-1)	Intensity (arbitrary units)	symmetry	IR active	type
2716	126	E'	yes	asymmetric stretch
2716	126	E'	yes	asymmetric stretch
2583	0	A1'	no	symmetric stretch
1213	14	E'	yes - weak	angle deformation
1213	14	E'	yes - weak	angle deformation
1163	93	E'	yes	umbrella

Ng611 (talk) 17:19, 30 May 2019 (BST) Try to use the correct terminology when describing the modes in your molecule (i.e.: in-plane/out-of-plane bends instead of 'angle deformation' or 'umbrella'. Otherwise, good IR analysis.

Predicted BH3 IR spectrum

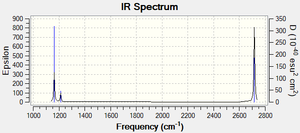
The symmetrical stretch does not lead to a change in dipole moment and so is not visibile in IR. The asymmetrical stretches and angle deformations are each degenerate, resulting in one peak for each mode.

MO diagram of BH3

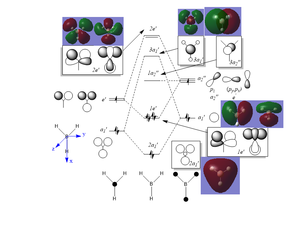
The MOs obtained through LCAOs closely match the ones predicted by Gaussian. Therefore, MO theory can reliably provide useful information on relative energy levels and bonding character.

Ng611 (talk) 17:22, 30 May 2019 (BST) Are there any significant differences?

NH₃ optimisation

Method: B3YLP

Basis set: 6-31G (d,p)

Gaussview summary table of an optimised NH₃ molecule

         Item               Value     Threshold  Converged?
 Maximum Force            0.000006     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000012     0.001800     YES
 RMS     Displacement     0.000008     0.001200     YES
 Predicted change in Energy=-9.843795D-11
 Optimization completed.
    -- Stationary point found.

Frequency calculation log file

 Low frequencies ---   -0.0140   -0.0032   -0.0015    7.0783    8.0932    8.0937
 Low frequencies --- 1089.3840 1693.9368 1693.9368

Optimised NH3 molecule

H₃NBH₃ optimisation and N-B bond energy

Method: B3YLP

Basis set: 6-31G (d,p)

Gaussview summary table of an optimised H₃NBH₃ molecule

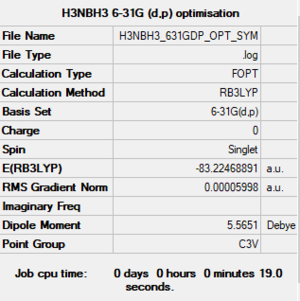
         Item               Value     Threshold  Converged?
 Maximum Force            0.000122     0.000450     YES
 RMS     Force            0.000058     0.000300     YES
 Maximum Displacement     0.000531     0.001800     YES
 RMS     Displacement     0.000296     0.001200     YES
 Predicted change in Energy=-1.655945D-07
 Optimization completed.
    -- Stationary point found.

Frequency calculation log file

 Low frequencies ---   -0.0251   -0.0030    0.0011   17.1236   17.1258   37.1326
 Low frequencies ---  265.7816  632.2034  639.3483

Optimised NH3 molecule

1 E_h= 2625.50 kJ mol ^-1

5 kJ mol ^-1 = 0.002 E_h

E(NH₃) = -26.615 E_h

E(BH₃) = -56.558 E_h

E(H₃NBH₃) = -83.225 E_h

$\mathrm{\Delta }$E = E(H₃NBH₃) - [ E(NH₃) + E(BH₃) ] = -0.052 E_h = -140 kJ/mol

The dative N-B bond has less than half the energy of the covalent N-B bond (389 kJ/mol), making it very weak in comparison.

Ng611 (talk) 17:24, 30 May 2019 (BST) You rounded too early. You should use the full precision values and round at the end. Remember that your values are accurate to about 5 d.p., NOT 5 s.f.. Also, you need to cite where you obtained your bond enthalpy value from.

NI₃ optimisation

Method: B3YLP

Basis sets:

• N: 6-31G (d,p)
• I: LanL2DZ

Gaussview summary table of an optimised NI₃ molecule

         Item               Value     Threshold  Converged?
 Maximum Force            0.000065     0.000450     YES
 RMS     Force            0.000038     0.000300     YES
 Maximum Displacement     0.000952     0.001800     YES
 RMS     Displacement     0.000415     0.001200     YES
 Predicted change in Energy=-5.172366D-08
 Optimization completed.
    -- Stationary point found.

Frequency calculation log file

 Low frequencies ---   -0.1614   -0.0983   -0.0031    0.5823    0.7024    1.5522
 Low frequencies ---  101.3248  101.3255  148.3662

Optimised NI3 molecule

Optimised N-I bond length: 2.184 A

Ng611 (talk) 17:25, 30 May 2019 (BST) Good!

Part II

[Cr(CO)₆]

Method: B3YLP

Basis sets:

• C, O: 6-31G (d,p)
• Cr: LanL2DZ

Gaussview summary table of an optimised [Cr(CO)₆] molecule

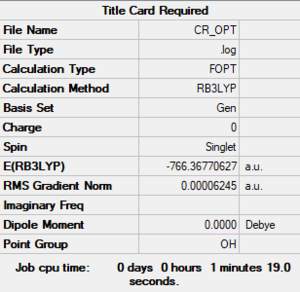
         Item               Value     Threshold  Converged?
 Maximum Force            0.000155     0.000450     YES
 RMS     Force            0.000063     0.000300     YES
 Maximum Displacement     0.000705     0.001800     YES
 RMS     Displacement     0.000378     0.001200     YES
 Predicted change in Energy=-2.394140D-07
 Optimization completed.
    -- Stationary point found.

Frequency calculation log file

 Low frequencies ---   -0.0011   -0.0010   -0.0009   11.7423   11.7423   11.7423
 Low frequencies ---   66.6546   66.6546   66.6546

[Cr(CO)6]

[Mn(CO)₆]⁺

Method: B3YLP

Basis sets:

• C, O: 6-31G (d,p)
• Mn: LanL2DZ

Method: B3YLP

Gaussview summary table of an optimised [Mn(CO)₆]⁺ molecule

         Item               Value     Threshold  Converged?
 Maximum Force            0.000045     0.000450     YES
 RMS     Force            0.000018     0.000300     YES
 Maximum Displacement     0.000344     0.001800     YES
 RMS     Displacement     0.000163     0.001200     YES
 Predicted change in Energy=-4.865686D-08
 Optimization completed.
    -- Stationary point found.

Frequency calculation log file

 Low frequencies ---    0.0010    0.0013    0.0014    6.1527    6.1528    6.1528
 Low frequencies ---   76.3733   76.3733   76.3733

[Mn(CO)6]+

[Fe(CO)₆]²⁺

Method: B3YLP

Basis sets:

• C, O: 6-31G (d,p)
• Fe: LanL2DZ

Gaussview summary table of an optimised [Fe(CO)₆]²⁺ molecule

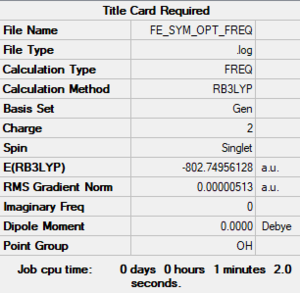
         Item               Value     Threshold  Converged?
 Maximum Force            0.000011     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000034     0.001800     YES
 RMS     Displacement     0.000015     0.001200     YES
 Predicted change in Energy=-4.521203D-10
 Optimization completed.
    -- Stationary point found.

Frequency calculation log file

 Low frequencies ---  -10.5131  -10.5130  -10.5130   -0.0009   -0.0004   -0.0002
 Low frequencies ---   82.0308   82.0308   82.0308

[Fe(CO)6]2+

Comparative analysis

The analysed compounds are isolelectronic and isostructural; therefore, the main differences should arise from the varying degree of backbonding between the metal centre and the $\pi$^*-acceptor carbonyl ligands. Thus, progressing across the row, the metal centre becomes more electropositive and the valence electrons are affected by an increasing Z_eff.

It is therefore expected that backbonding with the ligands should decrease as the valence electrons of the metal centre become more tightly held, with the valence 3d orbitals contracting, resulting in poorer overlap with the ligand frontier orbitals.

Since backbonding involves donation of electrons into the $\pi$^* orbital on CO, its decrease across the row could be observed as a lengthening of the M-C bond (which it would otherwise stabilise) and a shortening of the C=O bond (which it would otherwise destabilise).

Experimentally, this could be confirmed by IR spectroscopy (increasing CO stretching frequency) and, additionally, X-ray diffraction, for a general determination of all bond lengths.

Ng611 (talk) 17:35, 30 May 2019 (BST) Excellent rationalisation and good suggestions for experimental validation.

Predicted bond lengths, IR stretching frequencies and charge distributions

	M-C bond length (A)	C-O bond length (A)	C=O IR t1u stretching frequency (cm-1)	Charge on M (e)	Charge on C (e)	Charge on O (e)
[Cr(CO)6]	1.915	1.149	2086	-2.450	0.827	-0.419
[Mn(CO)6]+	1.908	1.136	2199	-2.048	0.834	-0.326
[Fe(CO)6]2+	1.942	1.125	2297	-1.503	0.815	-0.231

The simulation confirms the increased electropositive character of the metal centre and the increasing IR carbonyl stretching frequency, corresponding to a decrease of backbonding and strengthening and shortening of the C-O bond across the row. However, the predicted M-C bond lengths do not show the expected trend, with the Mn complex having the shortest M-C bond.

Generally, vibrational modes that have the same symmetry as quadratic functions (e.g. x², y², z² etc., as well as their linear combinations) are Raman IR active. Therefore, the symmetrical carbonyl a_1g and e_g stretching modes, which transform as (x²+y²+z²) and (2z²-x²-y², x²-y²) respectively, could be investigated using this technique.

Molecular orbitals

Molecular orbitals of hexacarbonyl complexes

a1g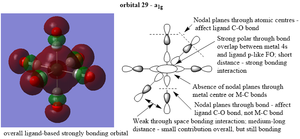
eg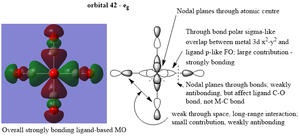
t2g

Ng611 (talk) 17:41, 30 May 2019 (BST) For your a1g orbital, what AO is that on the central metal atom? Is it s-type, or did you draw an (incorrect) dz^2 orbital? It's unclear. To cut down ambiguity, you could explicitly label the orbital.

Ng611 (talk) 17:45, 30 May 2019 (BST) In your eg orbital, the carbon interacts with the metal through an along bond p-orbital to form a sigma orbital. You then also have a sigma orbital between the carbon and oxygen, with the nodes passing through the C and O atomic centers.

Ng611 (talk) 17:45, 30 May 2019 (BST) Your t2g orbital is correct, well done!

In the case of $\pi$^* acceptor ligands, such as CO, the favourable interaction between the metal t_2g orbitals and the ligand $\pi$^* frontier orbitals leads to an increase of the splitting parameter $\mathrm{\Delta }$_oct.

This also gives rise to a corresponding set of t_2g orbitals (no. 56-58), which are expected to be higher in energy than the e_g orbitals of the metal complex.

However, due to the loss of precision of Gaussian when estimating higher-energy unoccupied orbitals, it has placed the aforementioned unoccupied t_2g orbitals lower in energy than the e_g orbitals (no. 65-66), which would otherwise be characteristic of a $\pi$ donor ligand.