User:Zw3812
Cope Rearrangement of 1,5-hexadiene
the Cope Rearrangment of 1,5-hexadiene is classified as [3,3]sigmatropic rearrangement and is widely studied. The mechanism of the rearrangement is thought to occur via either the chair-like structure or the boat-like structure transition states in concerted manner. The exercise aims to find the structures of the transition states and their energies on the potential surface using Gaussian calculation and the next section shows optimisations using Gauss to find structures of reactants( as well as product in this case) which are minimum in energy, ie the conformers of 1,5-hexadiene.
Optimising the Reactants and Product
the following table shows the various conformers of the 1,5-hexadiene, with their relative energies as compared to the lowest.
| structure No. | Caluclated Energy/ Hatrees (HF/3-21G) | Relative Energy with the lowest | Point Group | Image | Description | |||
|---|---|---|---|---|---|---|---|---|
| Gauche No.2 | -231.69266 | 0 | C1 |
|
Gauche structure No.2 is the global minimum state, whereby the dihedral angles are 120 degree between bond C12-C14 and bond C6-C9, 60 degree in the central and 120 degree between bond C1-C4. C1 point group. | |||
| Gauche No.7 | -231.69167 | 0.62 | C2 |
|
Gauche structure No. 7 has the angle between bond C7-C9 and bond C1-C4 being 124 degree, 60 degree for the two central carbons and the angle between bond C1-C4 and bond C12-C14 being 124. It is in C2 point group. | |||
| Gauche No.6 | -231.69153 | 0.71 | C2 |
|
corresponding to gauche structure 6, the dihedral angle between bond C12-C14 and bond C6-C9 is 109 degree, 60 degree for two central carbons and 109 degree between bond C6-C9 and bond C1-C4, It is in C2 point group. | |||
| Gauche No.8 | -231.68962 | 1.91 | C1 |
|
corresponding to gauche structure 5 on the table: the dihedral angles are 121 degree between bond C1-C4 and bond C6-C9, 60 degree for central carbon and 14 degree between bond C6-C9 and bond C12-C14, it is C1 point group. |
The following table shows the calculated energy and relative energies of different anti conformers.
| structure No. | Caluclated Energy/ Hatrees (HF/3-21G) | Relative Energy with the lowest | Point Group | Image | Description | |||
|---|---|---|---|---|---|---|---|---|
| anti No.1 | -231.69260 | 0.04 | C2 |
|
for anti No.1, dihedral angles are 65 degree between bond C12-C14 and C6-C9, 180 degree in the centre and 65 degree between bond C6-C9 and bond C1-C4, it has point group of C2. | |||
| anti No.2 | -231.69254 | 0.08 | Ci |
|
for anti No.2, the dihedral angles are 114 degree between C1-C4 and bond C6-C9, 180 degree in the central and 114 degree between bond C6-C9 and bond C12-C14, it has the point group of Ci. |
Generally the anti structures are more stable than gauche conformers, as the two alkene groups are furthest apart to eliminate steric reason. However, the global minimum corresponds to Gauche No.2, which could be due to the adhesion effect of the two H atoms within range of the covalent radii.<reference>1</reference>
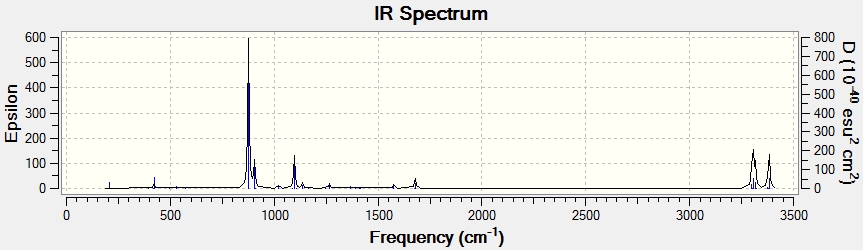
For the same structure of anti No.2, using different calculation method of B3LYP/6-31G*, energy of -231.5597 Ha is obtained. Meanwhile the structure underwent slight structural conformation, in which the dihedral angle between C1-C4 bond and C6-C9 bond changed from 114 to 118.8 degree and the same change occurred for bond C6-C9 and C12-C14. however the overall geometry did not change as it remains Ci as seen below, as well as an expected IR spectrum for this structure.
|
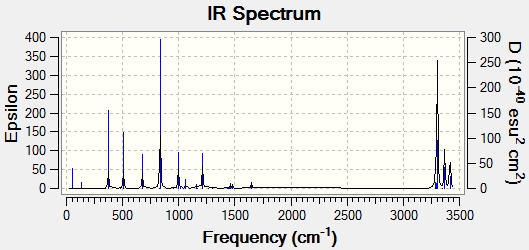 |
Table below shows the comparison of energies calculated using two different methods for the same structure of anti No.2
| type of energies | Caluclated Energy/Hatrees (HF/3-21G) | Caluclated Energy/Hatrees (B3LYP/6-31G*) |
|---|---|---|
| Sum of electronic and zero-point Energies | -231.53954 | -234.418888 |
| Sum of electronic and thermal Energies | -231.53257 | -234.412239 |
| Sum of electronic and thermal Enthalpies | -231.53162 | -234.411294 |
| Sum of electronic and thermal Free Energies | -231.57092 | -234.449554 |
Optimising the Chair and Boat Transition Structures
Three methods are used in finding the transition state of the Cope rearrangement, which can occur via either chair-like transition state or boat-like transition state.
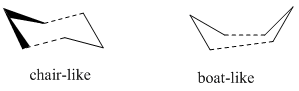
Chair Transition State
HF3-21G (Hessian) method
Allyl fragments which are the components that make up the transition states are drawn and optimised at HF/3-21G level of theory,with force constant being calculated (the Hessian), two of the fragments are arranged in the chair-liked orientation, and the distances between the terminal carbons are set to at 2.2 Å. The guess-ed transition structure is then put to calculation of frequency and optimisationwith force constant being calculated (the Hessian). The result of the electronic energy is -231.61932Ha and calculation of frequency and optimisation shows an imaginary frequency of -818.00 cm -1 and is corresponding to the Cope Rearrangement as shown by the animation below, as well as a predicted IR spectrum for this transition structure.
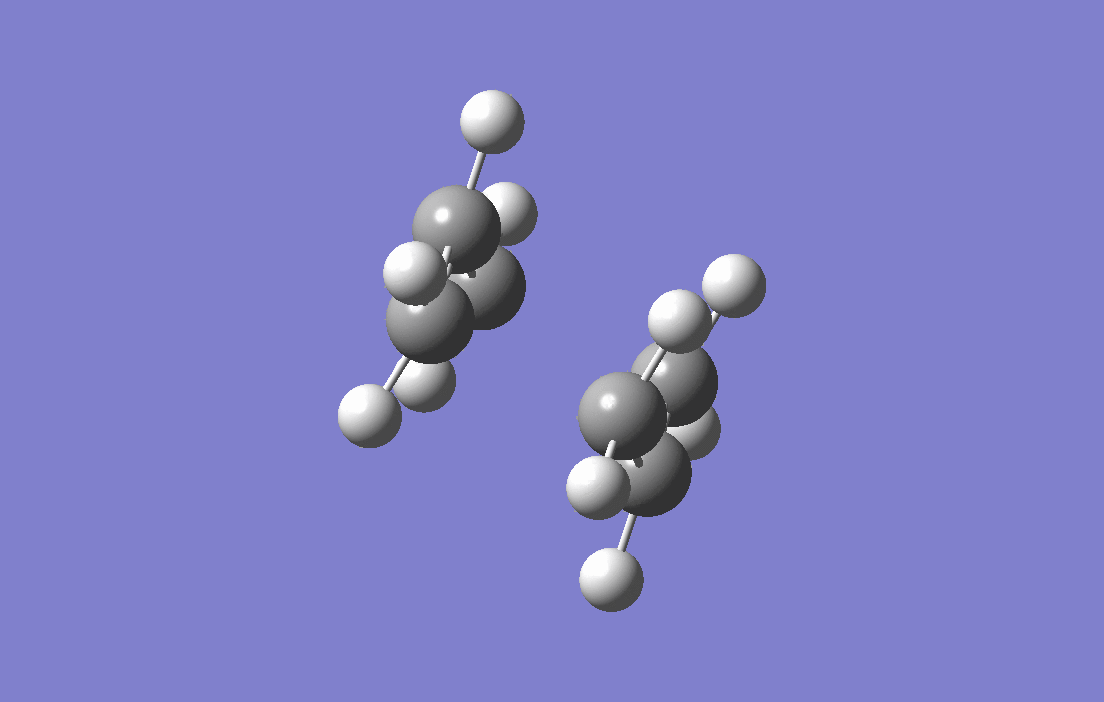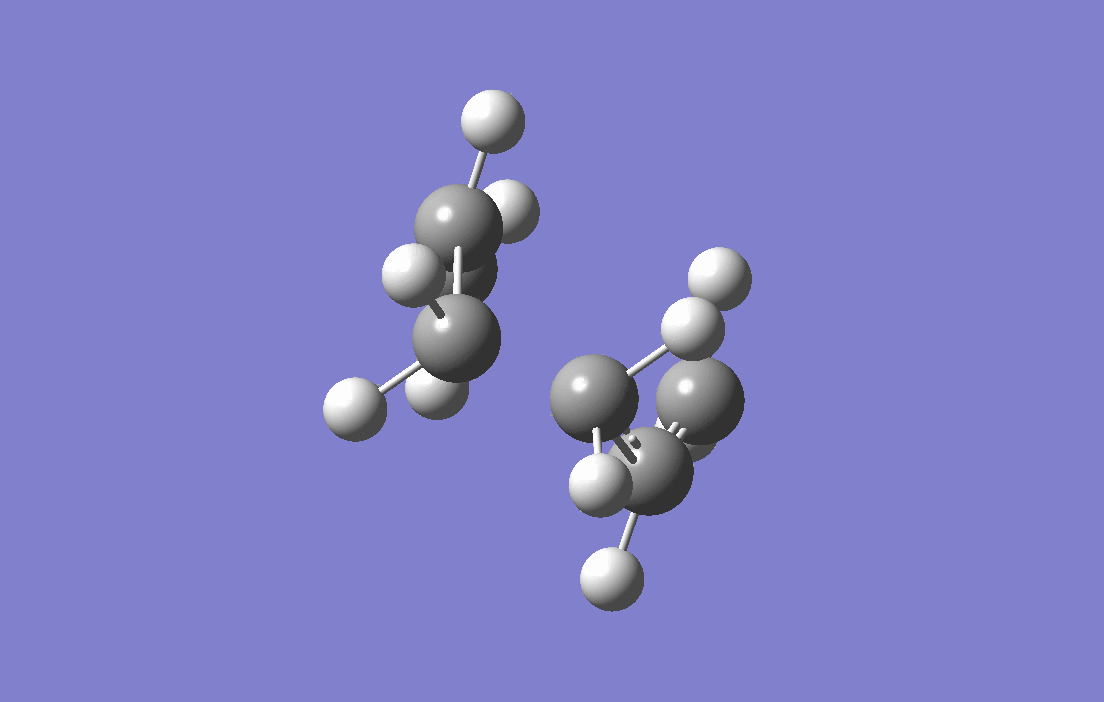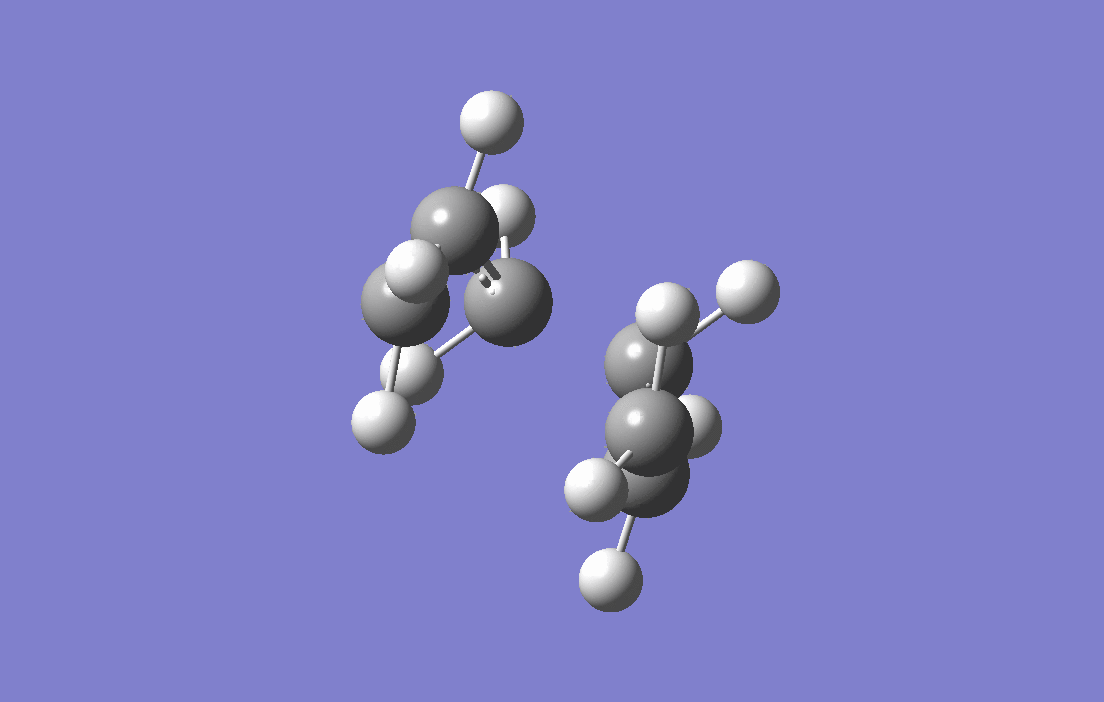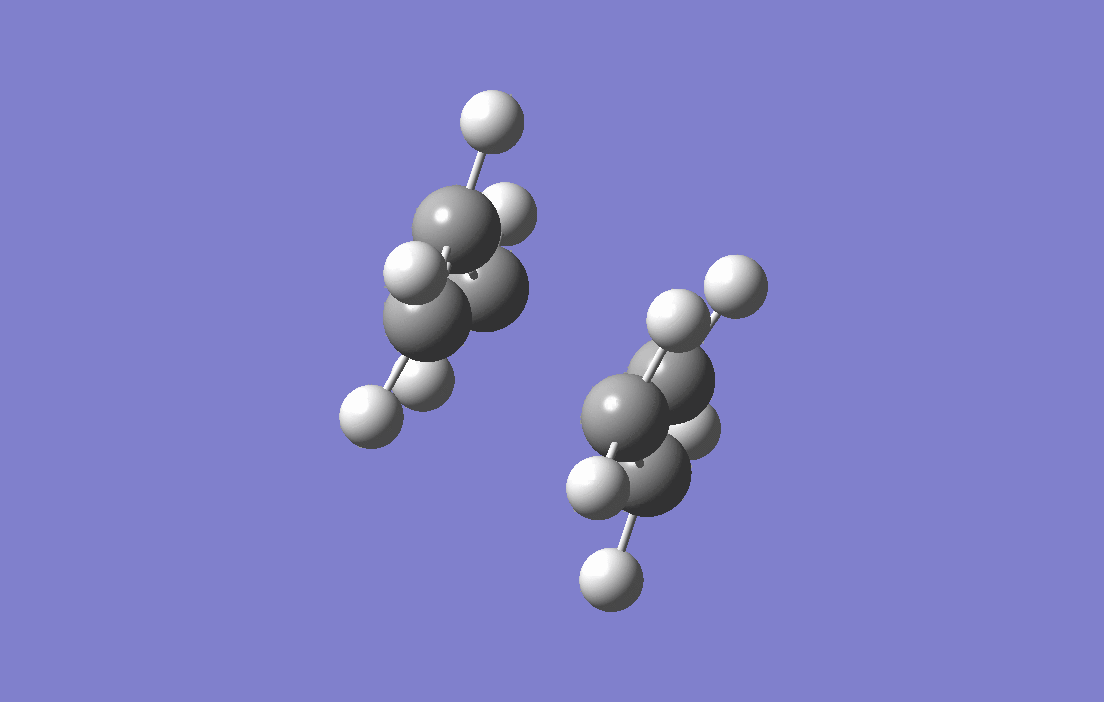 |
|
The previous step is repeated using the B3LYP/6-31G* level of theory and carried out frequency calculations as well. The electronic energy calculated was -234.55698Ha and an imaginary frequency at -566 cm-1. The geometry and spacial arrangement are very similar,but there is significant energy differences.
Freezing coordinate method
this method involves using Redundant Coord Editor to freeze the bond lengths of the newly formed σ C-C bonds to be 2.2 Å. By freezing the coordinates, the optimisition (HF/3-21G)calcultion shows the structure of the transition state to be the same as above, with the bond lengths fixed at 2.2 Å, as shown below.
Chair-like transition state |
The structure was reoptimised using a normal guess Hessian modifying the two differentiating coordinates which correspond to the two forming σ C-C bonds.The result is shown below.
Chair-like transition state |
the Transition state is then optimised and the energy obtained is the same as before which is -231.61932Ha. the two methods produced the same transition state with the energy, showing both are effective, because the guessed structure is very close to the "real" transition state structure brought out by calculation.
Boat Transition Structure
QTS2 method
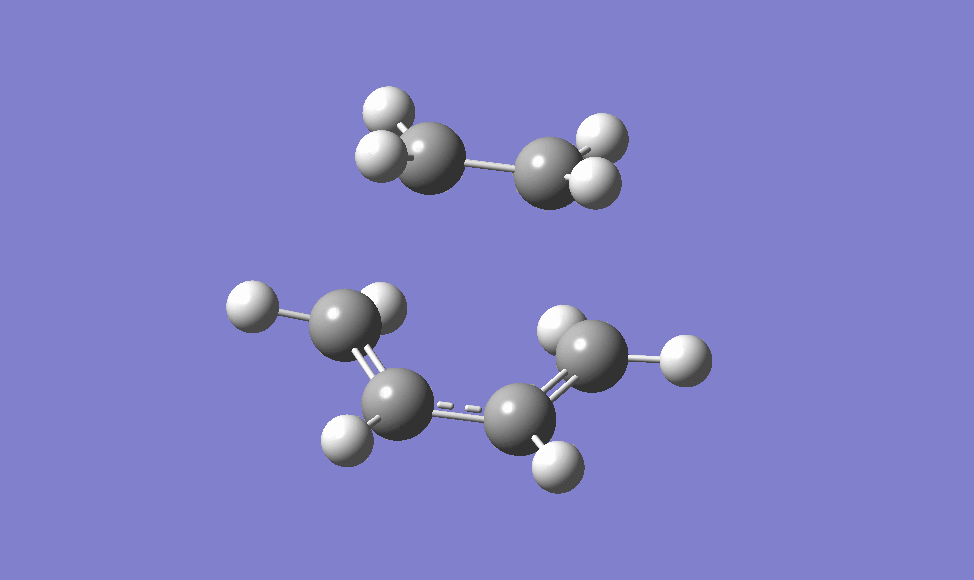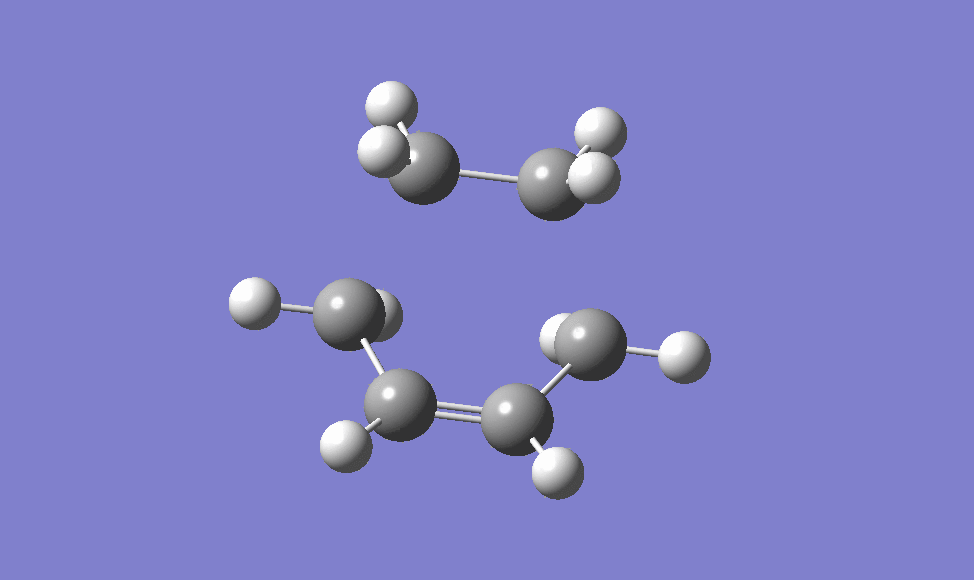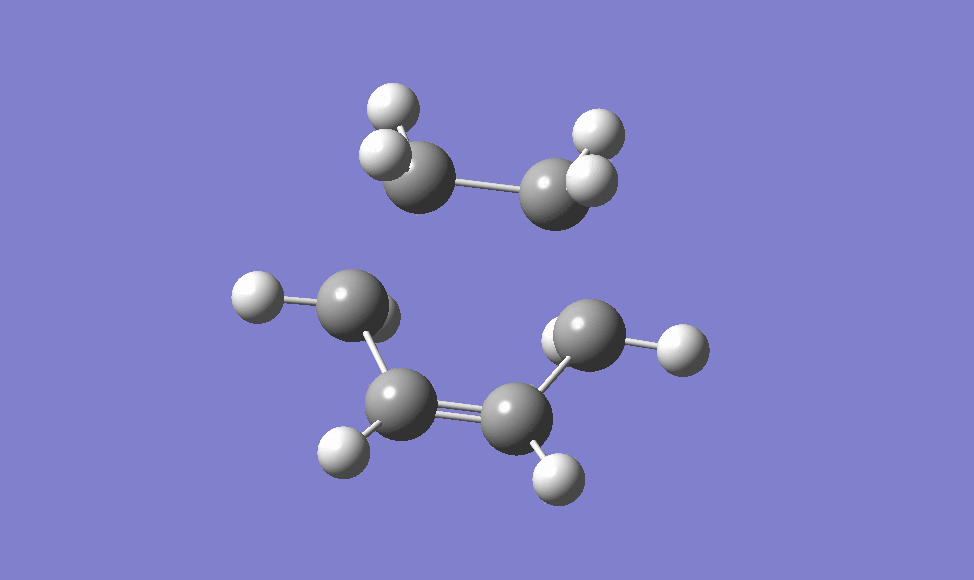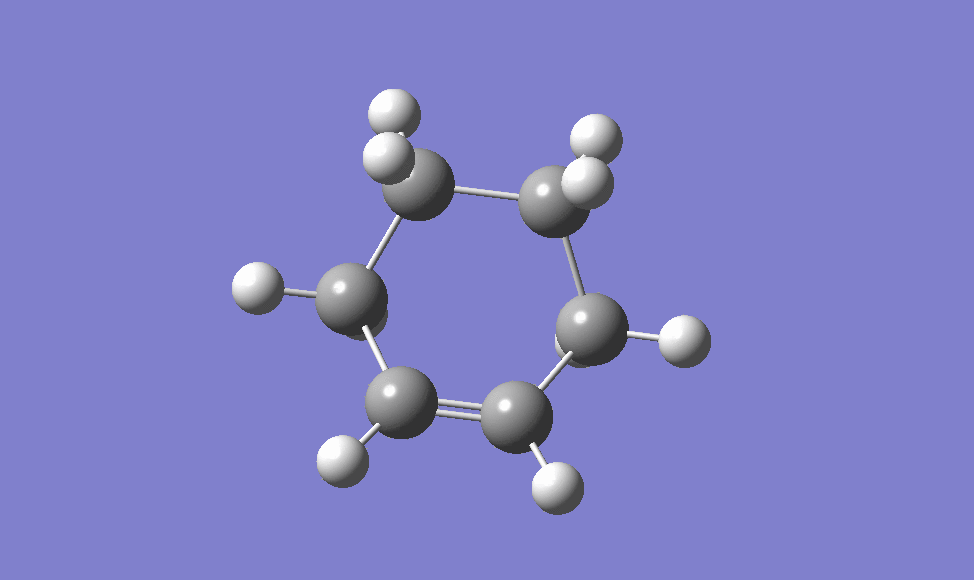
In finding the boat-like transition structure, the QST2 method is used. In this method, the structure of the reactant and product are drawn and the software is set to compute the transition structure between the two structures drawn. In this case, the reactant and the product are the same, therefore the atoms must be labeled for the software to recognise the starting point and end point of the reaction. Using the QST2 calculation, first the structure of the reactant and product are drawn as shown below, the labeling on the atoms are to show there is rearrangement.
However, after the calculation, a Chair-like Transition structure is present as shown below, and this is due to the limitation of the software in which the rotation around the central bond is not taken into consideration.
Chair-like transition state using QTS2 |
To avoid this limitation, the central bond are manually rotated in the product structure as shown below.
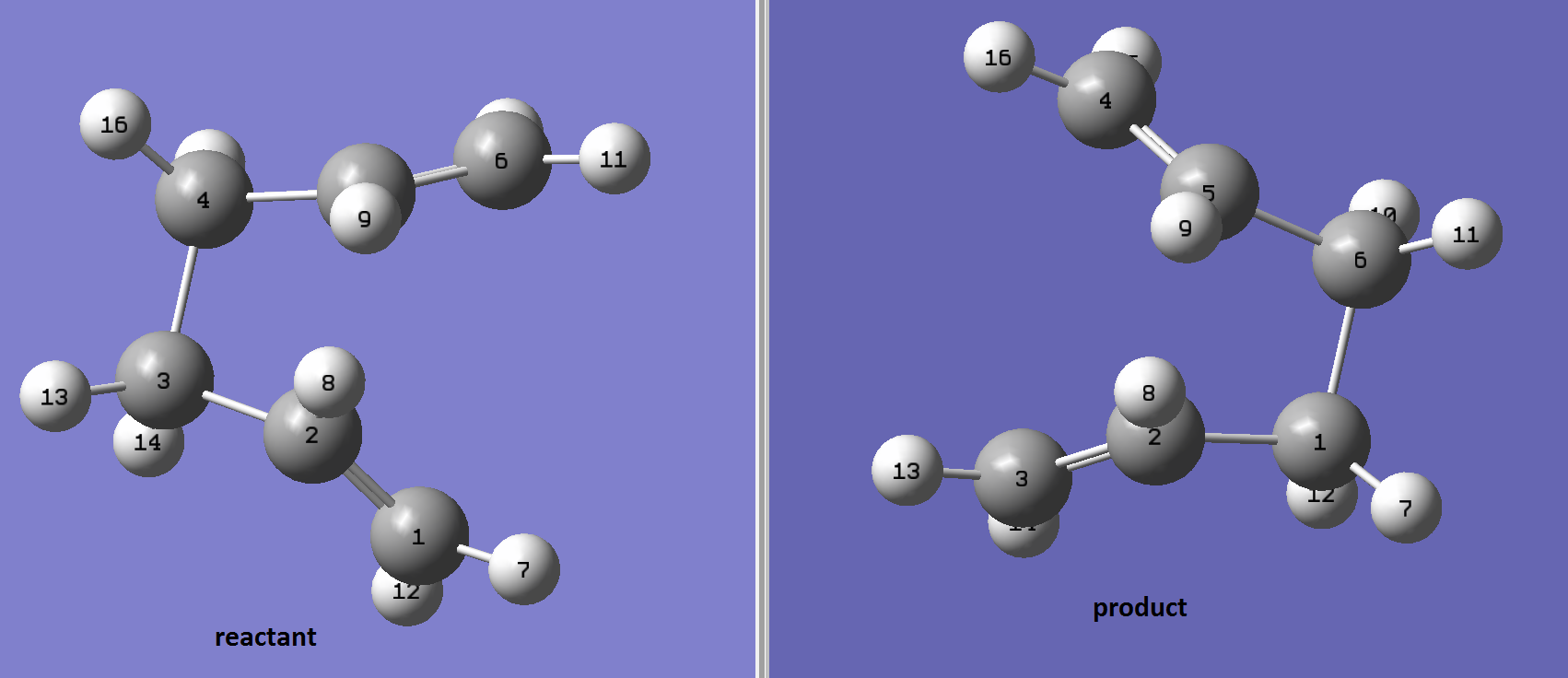
and the transition structure obtained using this method is the boat conformer.
boat-like transition state using QTS2 |
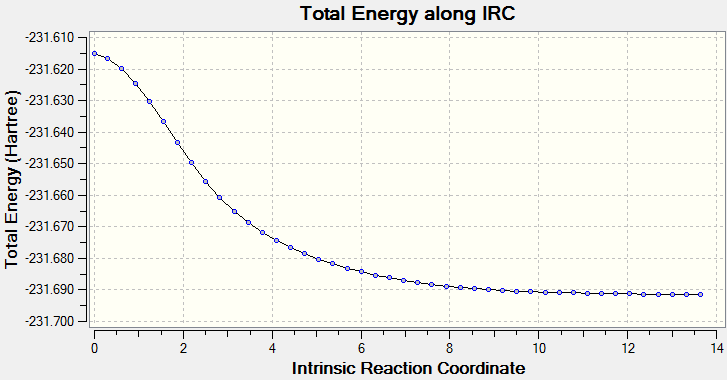
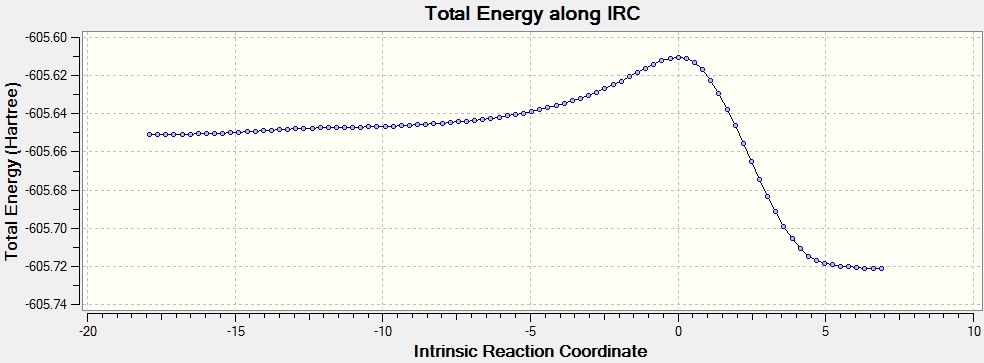
Intrinsic Reaction Coordinate
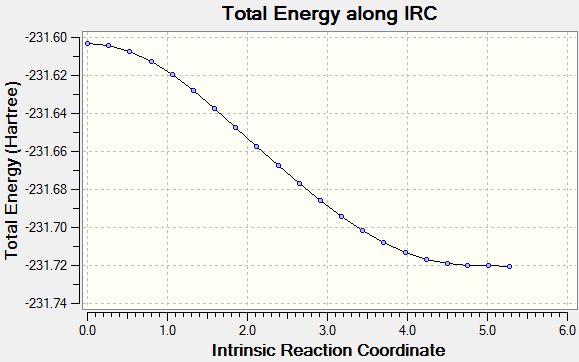
IRC method is used to determine which of the 1,5-hexadiene conformers the reaction follows as well as the pathway the reaction has taken via the chair-like transition state. Since the reaction is symmetrical, only the forward reaction going from the transition state to the product is shown. This result in the gauche 2 structure as on the Appendix I [1] or gauche No.7 as in table I shown above.
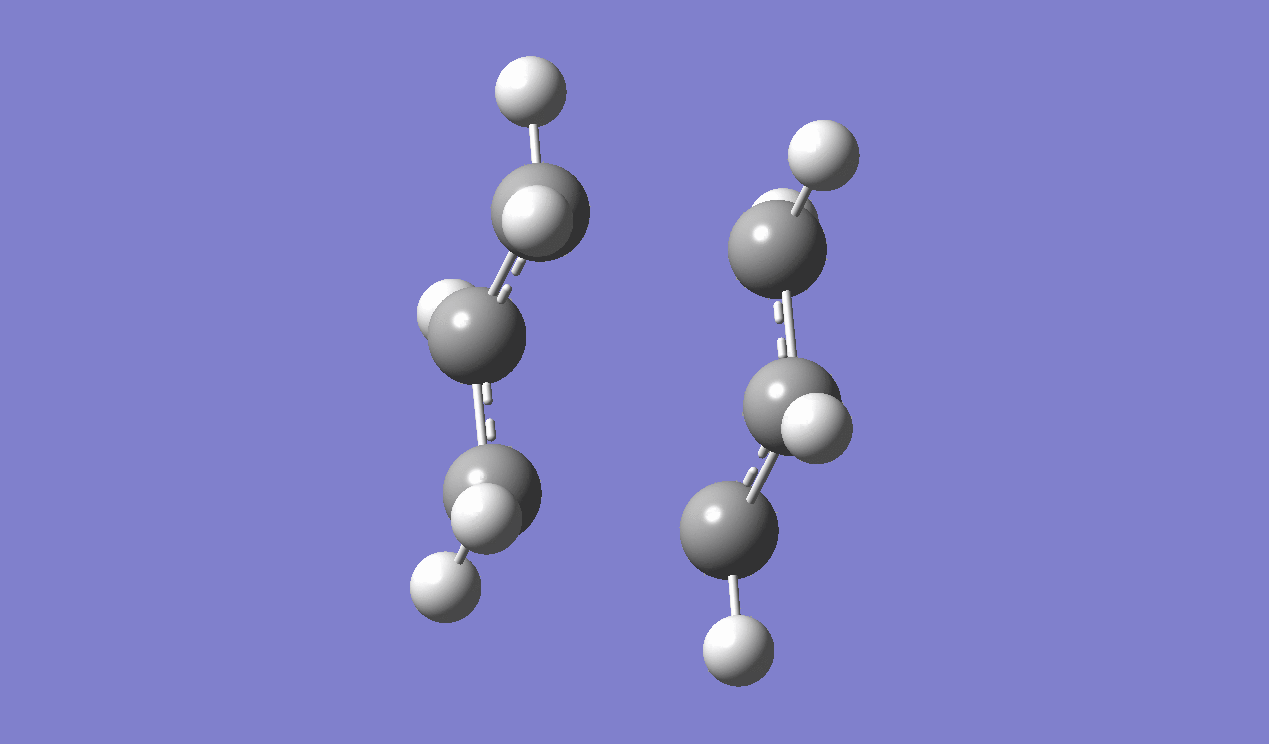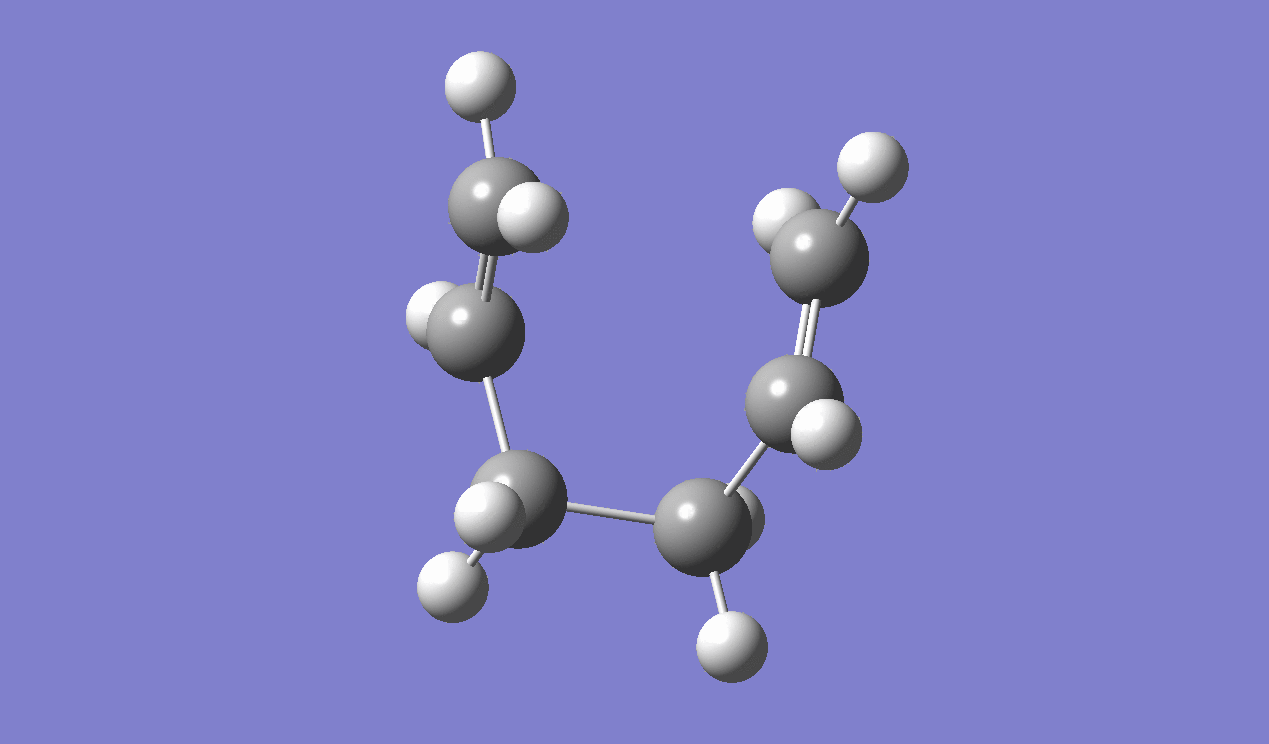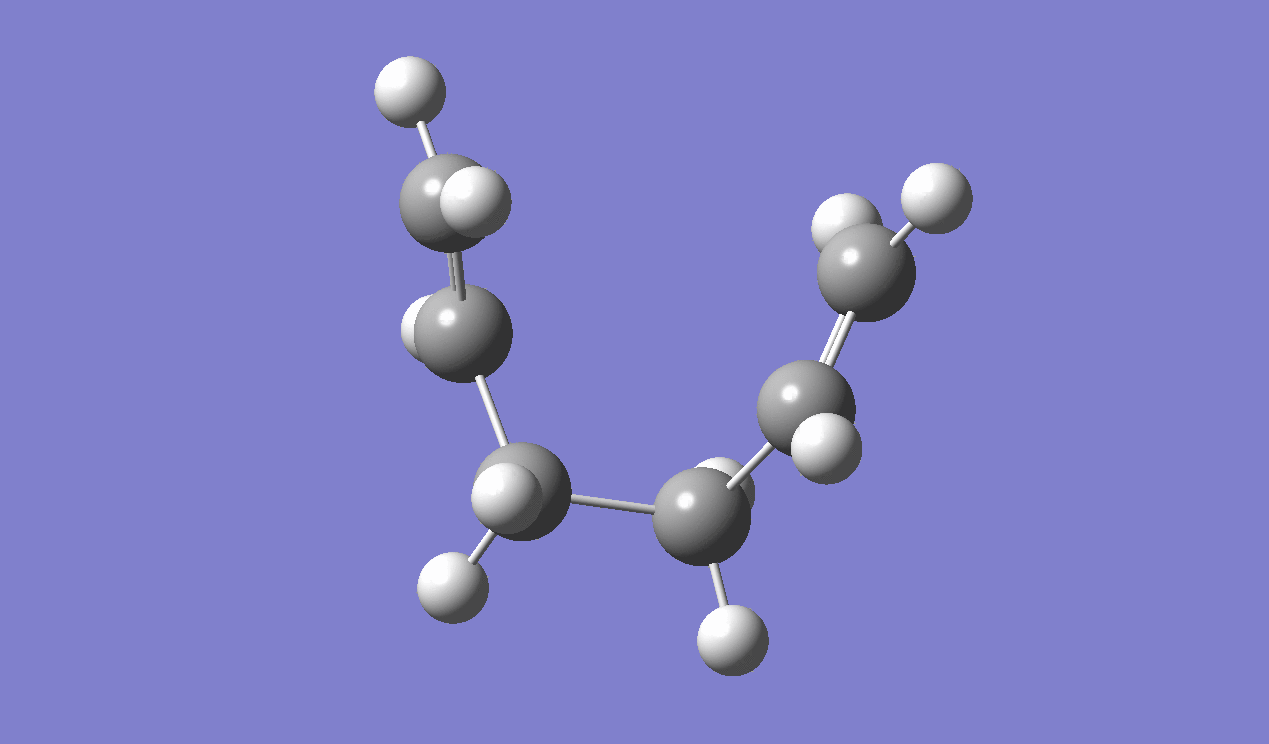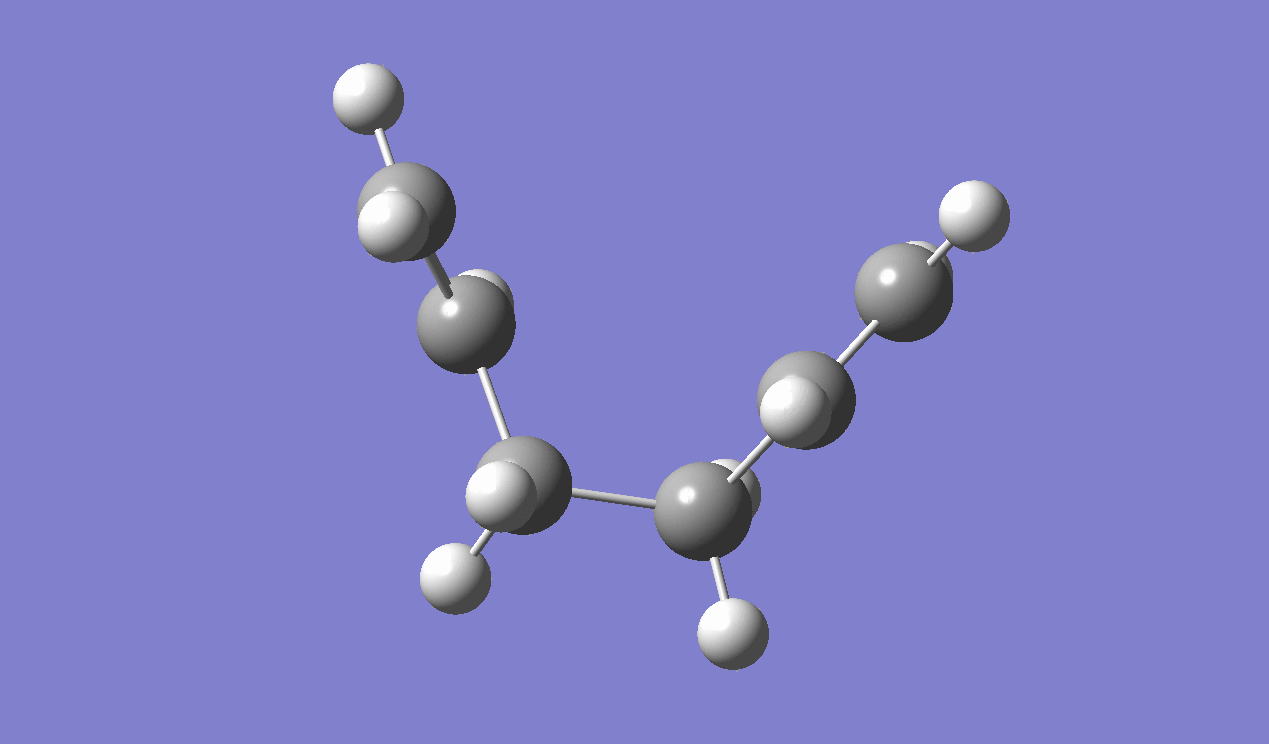 |
|
However this structure is not the minimum geometry, evident from table I. The IRC calculation is repeated with 150 points with force constant calculated at every step, aiming to find the structure with minimum energy, yet the result obtained is the same as before. An explanation is that the intrinsic reaction coordinate shows only the pathway with the deepest gradient,and this pathway may not be the same as the pathway that leads to a global minimum, or the transition state used would only lead the product shown, and other minimum structure must formed via different transition state. Therefore, conformer analysis must be conducted for future experiments.
Activation Energies
Below is the summary of activation energies calculated based on the total energies computed by Guassian using two different level of theory. The reactant is selected as the anti 2 conformer.
| HF/3-21G at 0K | HF/3-21G at 298.15K | B3LYP/6-31G* at 0K | B3LYP/6-31G* at 298.15K | Expt. at 0K | |
|---|---|---|---|---|---|
| ΔE (chair) in kcal/mol | 45.71 | 44.70 | 34.05 | 33.16 | 33.5 ± 0.5 |
| ΔE (boat) in kcal/mol | 55.60 | 54.76 | 41.96 | 41.32 | 44.7 ± 0.5 |
The chair transition structure has lower activation energy, hence conformers formed via the chair-like transition state are the kinetic product.It is also observed that B3LYP/6-31G* level of theory at 0K gives better result as the values are closer to the experimental.
The Diels-Alder Cycloaddition
The Diels-Alder cycloaddition is a concerted pericyclic addition, this reaction occurs via formation of new and stronger σ bond from two overlapping p orbitals by breaking weaker π bonds. The reaction is allowed only when there are good overlap between the orbitals with the right symmetry.
Cis Butadiene and ethene
Experimental
The HOMO and LUMO of cis butadiene are shown below
| HOMO | 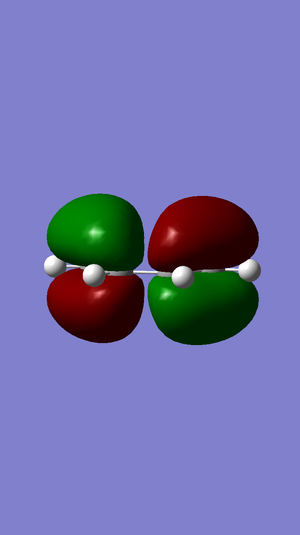 |
anti-symmetrical |
| LUMO | 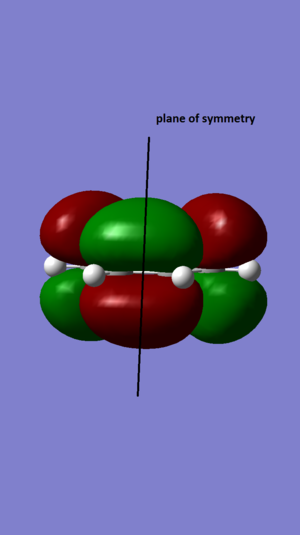 |
symmetrical |
the guessed transition state structure for this cycloaddition is drawn on the assumption that the transition structure is very similar to the final product, using Hammond's postulate [2] , therefore the guessed structure is drawn by removing the two newly formed σ C-C bonds. The structure is then optimised to a transition state (Berny) using HF/3-21G level of theory as it is the quickest method to do. The transition state is then obtained, as shown below, and it is confirmed via the IRC method and the animation of which is also shown below.
|
 |
|
The computation also shows the imaginary vibration frequency of -818.44 cm-1, which correspond to the formation of two σ C-C bonds, at the same time, as the terminal carbons are brought in closer by the vibrations allowing the orbitals to overlap.  The next positive vibration correspond to a swinging motion conducted by both molecule in the transition and this vibration does not help in bringing the orbitals closer for addition.
The next positive vibration correspond to a swinging motion conducted by both molecule in the transition and this vibration does not help in bringing the orbitals closer for addition.
Typical C-C single bond has bond length of 1.20 to 1.50 Å, [3] and the old C-C single bonds in this structure have bond lengths of 1.37 Å. the newly partially formed C-C bond has length of 2.20 Å. The van der Waals radius for carbon atom is 1.70Å, therefore the newly forming bonds are within the van der Waals radii of two carbon atoms.
The following table summaries the HOMO and LUMO of the transition structure shown above.
| HOMO of ts | 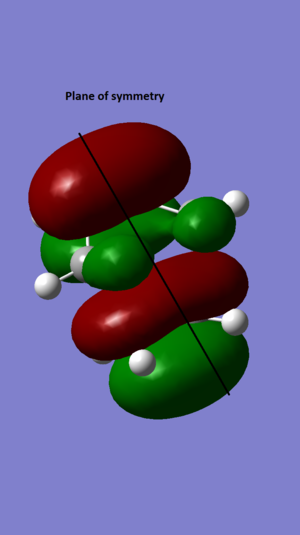 |
anti-symmetrical |
| LUMO of ts |  |
symmetrical |
Cyclohexa-1,3-diene with maleic anhydride
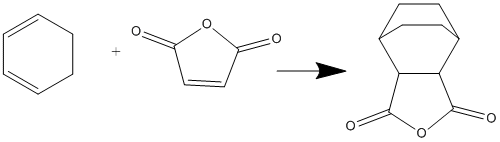
This reaction forms two products, one called the exo and the other endo. The following sections aim to find the energies differences between the two by finding the transition states, and hence rationalise the ratio in the products formed.
Exo Product
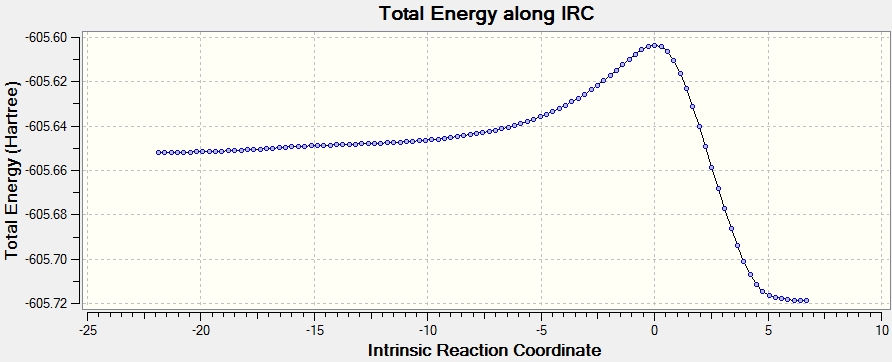
The transition state is determined using similar method as the cis butadiene, using Hammond's Postulate, and the structure is confirmed using IRC running in both direction following 250 points with force constant calculated at every step
|
 |
|
 |
HOMO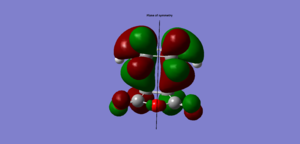 |
anti symmetric |
LUMO 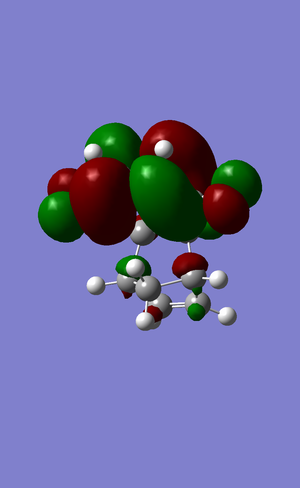 |
anti symmetric |
By comparing the IRC plot, it is clear the endo transition state has a lower energy compared to the exo by 0.68 Kcal/mol, as both transition states are optimised using HF/3-21G level of theory. Therefore the kinetic product is the endo product, due to lower kinetic barrier. Endo transition state has lower energy because there are less steric interactions between -(C=O)-O-(C=O)- fragment and the rest of the system. [4]
- ↑ https://wiki.ch.ic.ac.uk/wiki/index.php?title=Mod:phys3
- ↑ Anslyn, Eric V.; Dougherty, Dennis A. (2006). Modern Physical Organic Chemistry. Sausalito, CA: University Science.
- ↑ Handbook of Chemistry & Physics (65th ed.). CRC Press. ISBN 0-8493-0465-2.
- ↑ uhoadsghfio
endo product
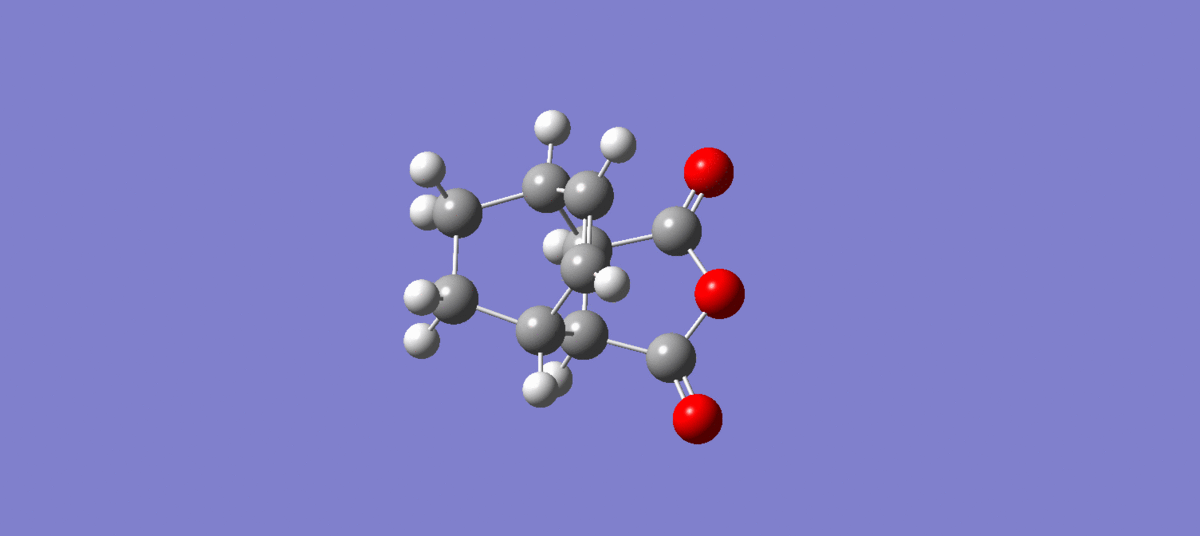
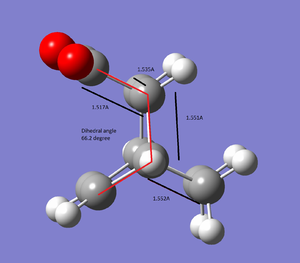
This transition state is determined using QTS2 method as described above.TS is confirmed using IRC in both direction following 250 points with force constant calculated at every step.
|
 |
| |||
 |
HOMO 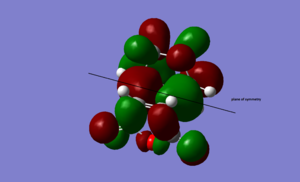 |
antisymmetric | |||
LUMO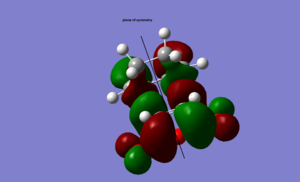 |
antisymmetric |
Endo transition state is lower in energy by 0.68 Kcal/mol than the exo, thus endo is the kinectic product as the kinectic barrier is lower. Both transition structure is optimised using HF/3-21G level of theory.
References
