User:Yqw13
Computation Introduction of Transition Structures of Pericyclic Reaction
Computation becomes a popular technique that makes effort to concentrate geometric energies and to solve problems of quantum chemical dynamics. With basis of theoretical chemistry and mathematical methods, computation contributes to many aspects of calculations including molecular geometry, molecular orbitals, transition state, etc. [1] As a purpose of the study, transition structures (TS) of pericyclic reactions, specifically Cope rearrangement and Diels-Alder cycloaddition, will be simulated by Gaussian 05 software in order for further investigation of their properties such as total energy and selectivity. Essentially, the change in potential energy during a reaction is constructed as a function of the nuclear positions, named as potential energy surface (PES). In order to determine TS (saddle point) geometry of a reaction, 1st and 2nd derivatives of energy are required to locate a stationary point where energy decreases in all direction (gradient = 0). Furthermore, minimum energy pathway (MEP) can be targeted among all possible trajectories on PES, where the most stable conformers of reagents and products are connected with TS. It is worth mentioning that there may exist more than one saddle points in a complicated reaction, i.e. global and local peaks. [2] In this specific case, it is assumed that only one TS is present during pericyclic pathway. However PES method is no longer sufficient for computing complex structures, e.g. Diels-Alder TS. Additional applications are demanded including MO-based method, etc.
Molecular geometry optimisation
This job is abbreviated as 'opt' with the purpose of geometry optimization. The input structure is adjusted in order to find the local minimal energy on the surface whose differentiation is zero. For example, Berny algorithm majorly acts on the recognition and optimizations of transition state via the Redundant option. This method is often applied when comparing the energies of different conformers hence their stability. [1]
Vibrational Frequency
This is another job type exclusively for stationary points, naming 'freq'. Basically it approximates force constant by 2nd differentiation of energy in terms of Cartesian-nuclear and mass-weighted coordinates, then vibrational frequencies and infrared intensities are further computed.The geometry is recommended to be optimised prior to frequencies calculation so that results will be more converged, in this case, a combination job Opt+Freq can be conducted. Frequency calculated also examines the performance of structure optimisation. It is noticeable that a successful minimisation of molecular energy is reflected by all positive vibrational frequencies, whereas for that of TS, one imaginary frequency will be present. [1]
Intrinsic Reaction Coordination (IRC)
This method is responsible for tracing in both directions from saddle point to minima in order to find the desired TS. Every point along the trajectory is optimised such that the gradients of the curve overlap with tangent of the path. TS geometry is adjusted to acquire a lower energy gradient hence lower pathway. Initial force constants is required to proceed IRC calculations, also isotopic input should be specified by labeling. [1]\
Nf710 (talk) 11:23, 25 February 2016 (UTC) Good brief understanding of the methods. but you havent shown any understanding of the theory.
Cope Rearrangement
Optimisation of Reactants and Products
Different conformations of 1,5-hexadiene molecule were optimised at HF/3-21G level of theory which are listed in the table along with their corresponding electronic energies and point groups. Proposed structures can be classified as 6 gauche and 4 anti-periplanar (anti) shapes. Commonly the energies of gauche conformers are predicted to be higher than those of anti, as they experience more steric effect. However the calculation at HF/3-21G level suggests that Gauche 3 possesses lower energy than Anti 2. Anti 2 is centro-symmetric with the point group of Ci (inversion operation). This contradiction may be resulted from the overlap between π* orbital of C=C bonds and sigma bonds of vinyl protons in Gauche 3, whose stereoelectronic attraction outweighs sterics hindrance. [3]
Nf710 (talk) 11:26, 25 February 2016 (UTC) You could have shown this with the orbitals from the .chk file
| Table 1. Conformations of 1,5-hexadiene after opt of HF/3-21G | ||||||
|---|---|---|---|---|---|---|
| Confomer | Structure | Energy HF/3-21G (Hartree) | Relative Energy (kcal mol-1) | Point Group | ||
| Gauche 1 | -231.687716 | 3.1029 | C2 | |||
| Gauche 2 | -231.691667 | 0.6237 | C2 | |||
| Gauche 3 | -231.692660 | 0.0000 | C1 | |||
| Gauche 4 | -231.691532 | 0.7094 | C2 | |||
| Gauche 5 | -231.689617 | 1.9109 | C1 | |||
| Gauche 6 | -231.689160 | 2.1967 | C1 | |||
| Anti 1 | -231.692603 | 0.0368 | C2 | |||
| Anti 2 | -231.692535 | 0.0789 | Ci | |||
| Anti 3 | -231.689071 | 2.2529 | C2h | |||
| Anti 4 | -231.690971 | 1.0607 | C1 | |||
(1 hartree = 627.509 kcal/mol)
However the energy difference between two structures is tiny therefore further comparison is carried out after optimisation at B3LYP/6-31G(d) level of theory. With the base of previous optimisation, Anti 2 geometry is readjusted by infinitesimal amount resulting in a slight decrease in electronic energy of ground state. Hence the molecule is further stabilised by a different method of calculation.
Nf710 (talk) 11:33, 25 February 2016 (UTC) You cannot compare the energies! they hav completely different hamaltonians
Specific changes in bond lengths and dihedral angles between carbons are listed below. Since the molecule is centro-symmetric, only half of structure needs to be taken into account. As observed in Table 2, relief of dihedral angle (C1=C2-C3-C4) is the dominant factor that lowers steric interaction and the energy, compared with minuscule changes of other parameter. As mentioned above, frequency are often computed to ensure the successful optimisation of geometry. For example, Anti 2 is not TS therefore all frequencies present are positive and real, i.e. energy has been minimised.
In addition, the relationship between thermal energy and temperature is listed in Table 3. All the calculations are set to 298.15 K by default, although the alternation can be achieved by the Temperature option. It is observed that all types of energies share the same value at 0 K. This can be the consequence of suppressed molecular excitation such that only ground electronic state and zero-point vibrational energy are accessible at 0 K.
| Table 3. Energy/Enthalpy terms of Anti 2 at temperatures of 0 K and 298 K | ||
|---|---|---|
| Energy/Enthalpy terms (Hartrees) | 0 K | 298 K |
| Electronic energy + Zero-point energy | -234.484751 | -234.469215 |
| Electronic energy + Thermal energy | -234.484751 | -234.461866 |
| Electronic enthalpy + Thermal enthalpy | -234.484751 | -234.460922 |
| Electronic free energy + Thermal free energy | -234.484751 | -234.500800 |
Study of Chair and Boat TS
.
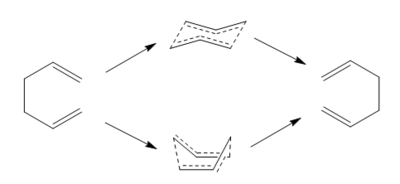
Cope rearrangement, also regarded as [3,3]-sigmatropic rearrangement, involves the migration of one σ-bond via a concerted transition structure. Reaction process is thoroughly reversible unless a stabilising group is applied to form an energy trap. There are two proposed conformations of TS --- "chair" and "boat" like, as shown in Figure 2. They will be analysed separately by different methods.
Chair conformation (C2h) is set up by oppositely orienting two allylic fragments in parallel with a rough separation of 2.2 Å. Subsequently the model built is undergone two distinct optimization processes. First method includes the computation of the force constant matrix with a sensible estimation of TS. Using combination job of Opt+Freq at HF/3-21G level, the structure is optimised to TS (Berny). The success of calculation is highly dependent on predicted geometry of TS. In case of the failure of TS optimisation, i.e. more than one negative frequency, calculation could be halted by the keyword Opt=NoEigen. Sometimes, optimisation could be reinforced by another methods yet at lower price, because it is not necessary to compute the entire force constant matrix. The second method involves the application of the keyword Opt=ModRedundant before optimising to TS(Berny), which freezes and energetically relaxes the geometry at the moment of bond breaking/formation at HF/3-21G level. Unfreezing process is required afterwards.
Results from both methods should be able to converge to a similar TS. The parameters given in Table 4 shows slight inconsistency due to different methods of calculation. Separation between terminals is consistently 2.02 Å which is smaller than the input (2.20 Å). There is only one imaginary frequency present in vibration list so that chair TS conformation has been optimised. The imaginary (negative) frequency is acquired from the negative force constant (k) due to the equation ω=√(k/μ). Force constant is calculated by the second derivative of potential energy relative to the displacement. Negative k value indicates a stationary point in nuclear configuration space which is also a maxima. Comprehensively, TS locates at the maxima where geometry is going towards either reactant or product. The physical significance is associated with the stretching of bonds which are being formed or broken. Therefore a structure should be re-optimised if more than one negative frequencies are present. [4]
Nf710 (talk) 11:39, 25 February 2016 (UTC) good understanding, but the first derivative is used to calculate if the PES is at a stationary point and the second derivative is used to calculate what tyoe
.
Boat TS conformation (C2v) is optimised by QST2 method. Optimised Anti 2 (1,5-hexadiene) structure is carried down as the shape of reactant and product, whose atom numbers are specified and matched as shown in Figure 3. Before processing the optimisation, Anti 2 structure needs to be shaped resembling the boat TS since the rearrangement process is not taken into account by Gaussian software. More specifically, Anti 2 is manually bent by setting dihedral angle (C2-C3-C4-C5) to 0o, and internal angles (e.g. C2-C3-C4) to 100o. TS is predicted by the maximal potential energy during linear interpolation between two molecules. The modified molecule is optimised using Opt+Freq at HF/3-21G level, then the interpolation is carried out by TS(QST2) option. Single negative frequency (-839.83 cm-1) suggests that boat TS optimisation is successful.
| Figure 4. Labelled reagent & product, and vibration of optimised boat TS | ||
|---|---|---|
| Reagent (Anti 2) | Product (Anti 2) | Boat TS |
|

|
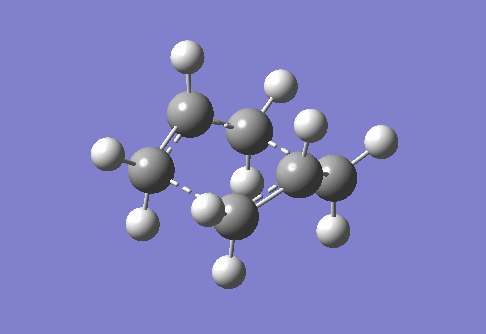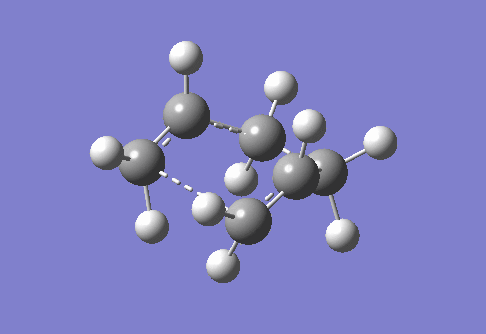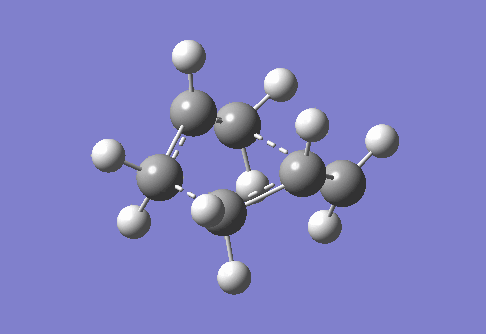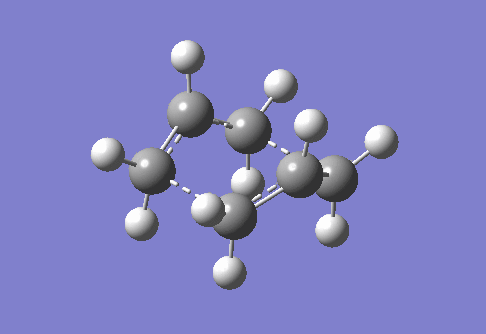
|
This section applies Intrinsic Reaction Coordination (IRC) to the chair conformation such that MEP is traced from the saddle point to local minima, hence desired TS can be found. Total energy of 50 geometry steps are computed along the trajectory to determine the steepest path on PES. A sufficiently large number of steps is recommended in order to enhanced the precision of IRC before the convergence of total energy. Symmetrical reaction coordinate allows IRC computing in a single direction (forward in this case).
.
| Figure 5. IRC trace and Energy-coordination graph of chair TS | |
|---|---|
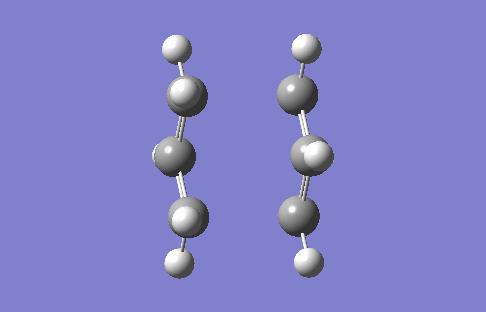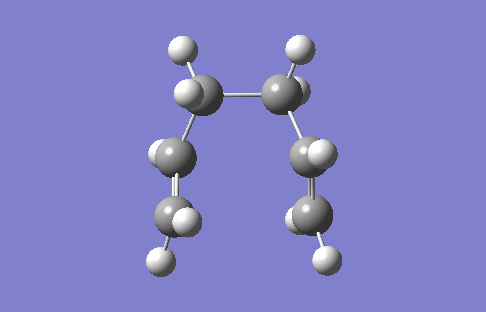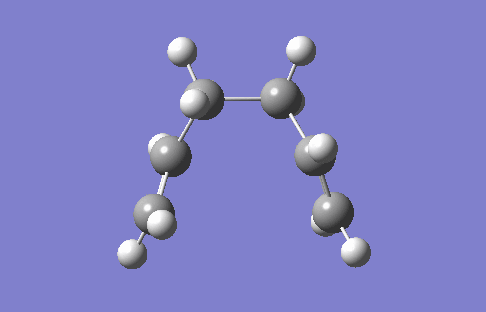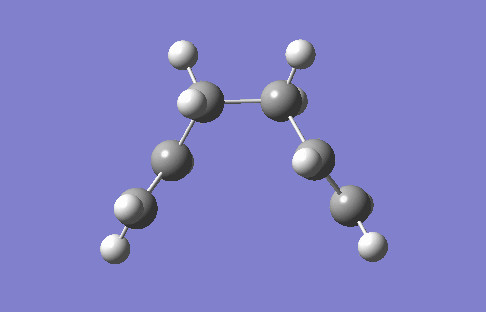
|

|
From the IRC plot above, the geometry at TS resembles Gauche 2 more than Gauche 3 (Table 1) although the latter possesses lowest energy. It is interestingly found that the trajectory does not necessarily pass through the conformation with lowest energy. According to Hammond's Postulate, smaller activation energy is achieved by resembling structures between reagent and TS, therefore the geometry whose energy is closest to TS is most likely to react. However HF/3-21G level of theory is insufficient for minimisation that gives the energy of -231.6152 Hartree. Performance of IRC at higher level of theory B3LYP/6-31G(d) is suggested. Or more expensively, IRC can be computed with force constant matrix at each single step, which provides the most reliable outcomes for small and medium systems.
Nf710 (talk) 11:47, 25 February 2016 (UTC) you could have optimised down the final structure to see what energy it went to.
| Table 5. Energy summary of chair and boat TS | ||||||
|---|---|---|---|---|---|---|
| Compound | HF/3-21G | B3LYP/6-31G(d) | ||||
| Electronic energy
(Hartree) |
Electronic energy
+ Zero-point energy at 0 K (Hartree) |
Electronic energy
+ Thermal energy at 298 K (Hartree) |
Electronic energy
(Hartree) |
Electronic energy
+ Zero-point energy at 0 K (Hartree) |
Electronic energy
+ Thermal energy at 298 K (Hartree) | |
| Chair TS | -231.619322 | -231.466700 | -231.461341 | -234.556980 | -234.414927 | -234.409007 |
| Boat TS | -231.602802 | -231.450930 | -231.445301 | -234.402340 | -234.402341 | -234.396006 |
| Reactant (Anti 2) | -231.692536 | -231.539542 | -231.532565 | -234.611711 | -234.469209 | -234.461869 |
Activation energies via both chair and boat conformations are present below. Electronic energy, electronic + zero-point energy (0 K), and electronic + thermal energy (298 K) are compared at different levels of theory. There are two apparent facts. Firstly, energies minimised by B3LYP/6-31G(d) is significantly lower than that by HF/3-21G due to a higher resolution by larger basis set. Secondly, energies of chair conformation are marginally lower than that of boat structure, hence chair TS is slightly more favoured. Comparing two geometries, it is evident that hydrogens at terminals of chair is staggered, but eclipsed at terminals of boat. Since hydrogens are not on neighboring carbons, steric contribution is not significant hence relatively the small energy difference between two geometries. Contribution of temperature is also studied by computing TS at 0 K and 298 K, respectively. Activation energies computed at B3LYP/6-31G(d) level of theory are approaching experimental values more, while the results from HF/3-21G are significantly overestimated.
| Table 6. Activation energy of TS at different temperatures (kcal mol-1) | |||||
|---|---|---|---|---|---|
| HF/3-21G | B3LYP/6-31G(d) | Expt. | |||
| 0 K | 298 K | 0K | 298 K | 0K | |
| Eact (chair) | 45.7083 | 44.6963 | 34.0687 | 33.1845 | 33.5 ± 0.5 |
| Eact (boat) | 55.6040 | 54.7606 | 41.9549 | 41.3238 | 44.7 ± 2.0 |
.
Nf710 (talk) 11:53, 25 February 2016 (UTC) Your energies are correct well done. but please dont compare energies. you havent come to the conclusion that lower basis sets still gove good approximations to the energy. but in general a well written report but you could have shown a greater understanding of the theorey
Diels-Alder Cycloaddition
Among all the cycloaddition reactions, Diels-Alder is characterised by [4s + 2s] concerted, pericyclic pathway between a diene (4 carbons + 4 π electrons) and a conjugate dienophile (2 C + 2 πe-). There are overall 6 πe- s participating in the reaction and two σ-bonds being formed. Diene is usually more electron-rich than dienophile hence electrons are transferred from HOMO of diene to LUMO of dienophile. This is regarded as the normal demand. But electron density can be reverted by attaching substituents, and so it is called inverse demand. Fragmental orbitals (FO) from two reagents overlap 'end on' to generate σ bonds. Same symmetry and small energy difference of FO ensure significant overlapping effect. For example, Ψ2 FO (diene) ↔ π* (dienophile) is present at normal demand, also π (dienophile) ↔ Ψ3 FO (diene) at inverse demand. Moreover Woodward–Hoffmann rules are closely associated with the accessibility of Diels-Alder reaction. Based to the rule, a thermally allowed pericyclic reaction must possess an odd number output from equation (4r+2)s + (4q)a, where ''s'' stands for superfacial orbital interaction and ''a'' for antarafacial. Other factors, such as the geometry of diene, has to be considered, since s-cis conformation of diene is necessary for the synchronised breaking/formation of the bonds.[5]
In this section, TS of two Diels-Alder cycloadditions will be computed and characterised using TS(QST2) method at different levels of theory, again the reaction path will be studied by IRC. Geometries are optimised via HF/3-21G, B3LYP/6-31G(d), and semi-empirical AM1 methods.
Cycloaddition of cis-butadiene and ethene
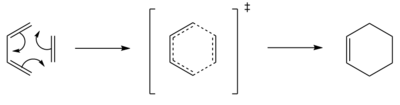
Reagents are set up by building cis-butadiene and ethene molecules that are optimised via semi-empirical AM1. Alternatively one can minimise energy using HF/3-21G + B3LYP/6-31G(d) which is highly time-consuming yet gives slightly better results. The frontier orbitals of each reagent, i.e. HOMO and LUMO, are illustrated in Table 7 accompanied with their symmetry. Symmetry of MO is determined respect to the vertical mirror plane. As mentioned above, orbital overlap is magnified by the same symmetry. Therefore HOMO of butadiene (AS) with LUMO of ethene (AS), LUMO of butadiene (S) with HOMO of ethene (S) are two plausible interactions, although the latter is less likely to occur owing to more significant energy difference. Eventually only the interaction of two AS orbitals is accessible that obeys the mode of normal demand.
| Table 7. HOMO and LUMO of reagents in prototypical cycloaddition | ||
|---|---|---|
| HOMO | LUMO | |
| cis-Butadiene | 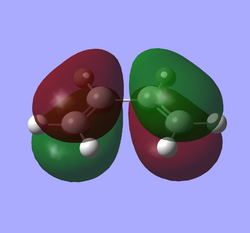
|

|
| Anti-symmetric (AS) | Symmetric (S) | |
| Ethene | 
|

|
| Symmetric (S) | Anti-symmetric (AS) | |
Subsequently, two optimised reagents are utilised to compute cycloaddition TS using TS(QST2) method, where reagents and product should be built and labelled in the same manner as for Cope reaction. First, optimised butadiene and ethene molecules are modified to an estimated shape of cycloaddition TS using bicyclo-octane as a template, so that the optimal overlap of π system can be acquired. Product molecule (cyclohexene) is refined at HF/3-21G + B3LYP/6-31G(d) levels of theory. The following label process is very essential for the success of TS computing.
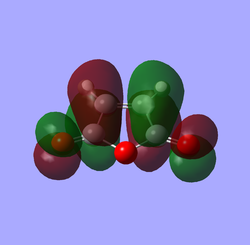
Table 8 below illustrates the structure, reaction path, and two vibration modes of prototypic TS. Single imaginary frequency reflects a complete minimisation of TS energy. All carbon-carbon bonds in TS (except two σ-bonds forming) are in the state between single (sp3) and double (sp2) bond, which is also suggested by Figure 6 and Table 8. The TS static plot shows the tiny difference between bond lengths (~1.38 Å) in TS. Typical bond length for sp3 carbon is 1.54 Å, and that of sp2 carbon is 1.33 Å.[6] Concluded from the comparison, sp2 C=C bond extends to a small amount, whereas the contraction of sp3 C-C bond is significant. If considering the orientation of p-lobes, little reorganisation of central p-lobes on diene is required to form a new π-bond with neighboring p-lobe. However the terminal p-lobes of diene form σ-bonds with that of dienophile, and remarkable reorientation is required in this case. As a result, the proposed stage of TS might resemble sp2 more than sp3 due to the ease of C=C bond formation. Two partly formed σ-bonds (2.22 Å) are much longer than C-C single bond, but shorter than twice of Van der Waal's radius of carbon (1.70 Å),[7]. It proves the existence of orbital overlap between 2 carbons.
Superfacial (s) interaction exists between p-lobes of two reagents which gives rise to (6 πe-)s and (0 πe-)a. According to Woodward–Hoffmann rules, the output of equation (4r+2)s + (4q)a is 1 + 0 = 1 (odd), hence this reaction is thermally allowed. TS vibration at imaginary frequency demonstrates the synchronous formation of σ-bonds that is supported by IRC plot. This vibration mode is favoured over that at lowest positive frequency (asynchronous), because [4+2] TS is able to rearrange towards a flat 6-membered ring. 6πe- obeys Hückle's Law (4n+2) hence the ring acquires aromatic character which stabilises TS and lower the energy. Furthermore, vibration at imaginary frequency involved the motion that benefits bond formation, whereas the orthogonal motion at real frequency does not. Thus IRC reaction path only includes the mode at former frequency rather than the latter.
Interestingly, HOMO of TS is symmetric respect to vertical plane, which contradicts to the previous orbital symmetry of reagents (both AS). However the reason could be an issue of relative orbital energies. Noticed that energy difference between HOMO and HOMO-1 (~0.002) are five-time smaller than that between other HOMOs or LUMOs (~0.01). The HOMO plotted is likely to be a flaw at B3LYP/6-31G(d) level of theory. HOMO-1 orbital might actually plays the role of HOMO during Diels-Alder cycloaddition.
(Very good. An MO diagram would explain why the HOMO and HOMO-1 cross over. Tam10 (talk) 13:57, 24 February 2016 (UTC))
| Table 9. Frontier orbitals of cycloaddition TS 6-31G(d) | |||
|---|---|---|---|

|

|

| |
| Orbital | LUMO | HOMO | HOMO-1 |
| Symmetry | S | S | AS |
| Relative energy | 0.14242 | -0.30086 | -0.30293 |
.
Regioselectivity of Diels-Alder reaction
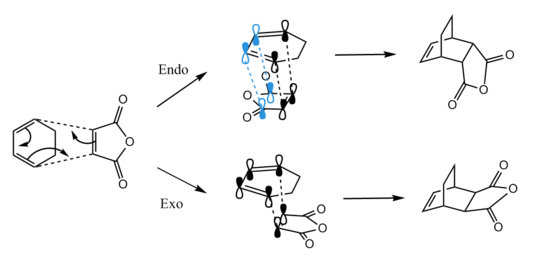
Regioselectivity should be taken into account when the substituents attached on diene and dienophile exert additional orbital interactions. For example, 1,3-cyclohexadiene and maleic anhydrase are typical reagents for studying exo and endo selectivity of cycloaddition as secondary orbital overlap is accessible. Resembling the method of protoypical reaction, the energies of 1,3-cyclohexadiene and maleic anhydrase are minimised using HF/3-21G and B3LYP/6-31G(d), respectively. Frontier orbitals of each reagent are illustrated in Table 10. Same symmetry and small energy difference are necessary for optimal orbitals interaction, however two possible outcomes arise from attached substituents --- endo & exo TS (Figure 7). Furthermore endo regioselectivity of a reaction displays the inverse demand, i.e. interaction between LUMO of the diene and HOMO of the dienophile.[8] Both TS will be computed by QST2 at two levels of theory, and their relative electronic energies are analysed.
(Maleic anhydride Tam10 (talk) 13:57, 24 February 2016 (UTC))
| Table 10. HOMO and LUMO of reagents in regioselective cycloaddition | ||
|---|---|---|
| HOMO | LUMO | |
| 1,3-Cyclohexadiene | 
|

|
| AS | S (diene part) | |
| Maleic anhydrase | 
|
|
| S | AS | |
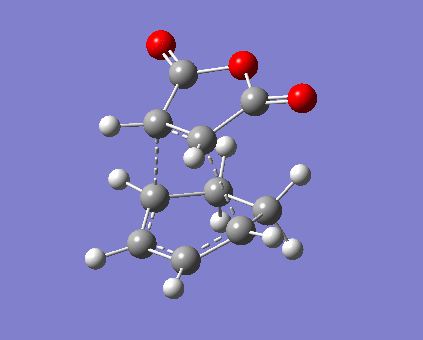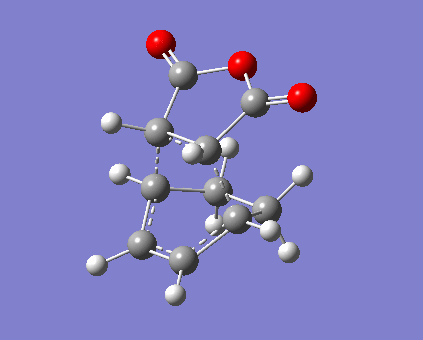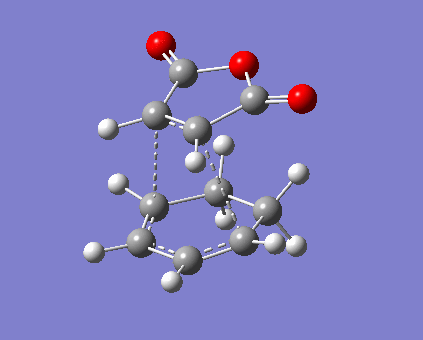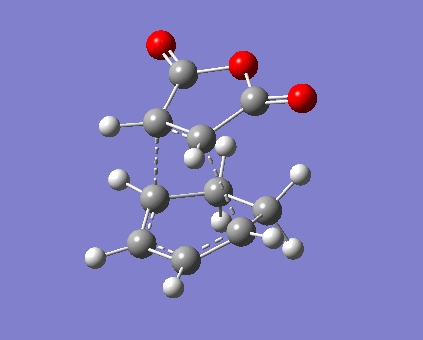
The situation of bond stretch and contraction is similar to those of prototypical reaction. Formation of 2 σ-bonds are synchronised in both endo and exo reaciton via a 6-membered ring, so the bond lengths should be symmetric during the formation. Specific distances between atoms are displayed in Table 11. In this case fragment -(O=C)-O-(C=O)- is focused on as it carries p-lobes orthogonal to the plane of anhydrase. Secondary orbital overlap exists in endo TS, as illustrated in Figure 7, where the p-lobes on C=O is aligned with those on diene. Currently the stereoelectronic attraction on carbon outweighs the steric interaction with sp2 C-H bonds (planar) on diene, and the partly formed σ-bonds are shorter compared with the value in prototypical reaction. In contrast, exo TS interaction is dominated by steric repulsion. Not only the absence of secondary interaction, C=O bonds directly clashes with sp3 C-H bonds (tetrahedral), i.e. greater steric effect and strain.[8] As a consequence, both carbon separation and the partly formed σ-bonds are averagely larger than those in endo TS. Furthermore, total electronic energy of exo TS is higher than that of endo which will be mentioned below (Table 13).
| Table 11. Structures and vibrations of endo and exo TS | |||||
|---|---|---|---|---|---|
| Endo TS and bond lengths | Exo TS and bond lengths | ||||

|
| ||||
| Endo vibration at -449.14 cm-1 | Exo vibration at -450.82 cm-1 | ||||
HOMO of two TS are illustrated here to explain the lower energy of endo TS caused by secondary orbital interaction, but absent in exo. Because total electronic energy of a molecule is solely related to occupied MOs. Both HOMOs have great electronic density between two reagents and small density around each C=O bond. It is clearly shown from MO that e- density around C=O overlaps with the bulk of π-system to some extent in endo TS, while these two regions become staggered in exo TS. There are also small orbitals around sp3 C-H bonds but interaction hardly occurs. In conclusion, secondary overlap is referred to the non-direct interaction between orbitals with the same symmetry. It is not necessary to form a bond, but a net decrease of energy (stabilisation) will be observed. [8]
| Table 12. Frontier orbitals of two TS | ||
|---|---|---|
| endo TS | exo TS | |
| HOMO | 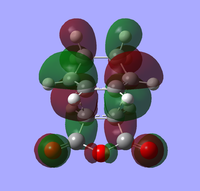 Front Front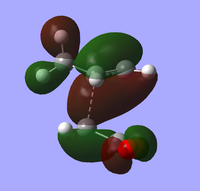 Side Side
|
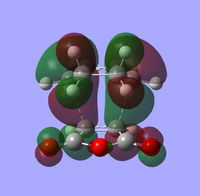 Front Front Side Side
|
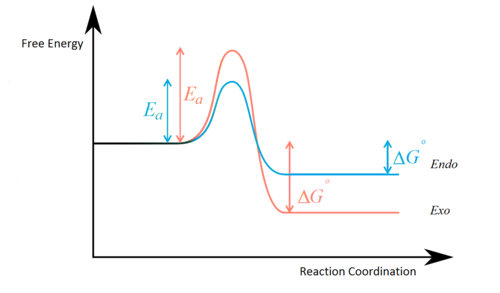
Energies of TS are computed at HF/3-21G and B3LYP/6-31G(d) levels of theory in QST2 jobs, which are summarised in Table 13. Compared with energies of Cope rearrangement, cycloaddition undergoes the exothermic pathway with deeper energy, since two strong σ-bonds are formed with the small penalty of breaking weak π bonds. The data output is relatively consistent with the energy profile in Figure 8 --- Eendo TS < Eexo TS ; Eexo product < Eendo product. This is resulted from the compromise between stereoelectronic and steric effect by TS and product. So far endo is defined as the kinetic product which is rapidly formed due to lower energy barrier. However small Eact also facilitates the reversibility of the reaction and eventually an exo (thermodynamic) product may be generated after a period of time. In term of calculation methods, B3LYP/6-31G(d) usually provides the further-minimised energy than HF/3-21G because a larger basis set is utilised and electronic correlation is taken into account. [1] It is worth mentioning that the output of Eendo product is lower than Eexo product at HF/3-21G level of theory, yet reverse is obtained by B3LYP/6-31G(d). Therefore higher resolution is recommended for optimising complex molecules with small energy difference.
| Table 13. Summary of reaction energy via two TS | ||
|---|---|---|
| Energy term (Hartree) | HF/3-21G | B3LYP/6-31G(d) |
| E1,3-cyclohexadiene + Emaleic anhydride | -605.646744 | -612.723684 |
| Eendo TS | -605.610368 | -612.698361 |
| Eendo product | -605.721321 | -612.772769 |
| Eactivation of endo reaction | 0.036376
(22.826267 kcal mol-1) |
0.025323
(15.890410 kcal mol-1) |
| Eexo TS | -605.603591 | -612.694415 |
| Eexo product | -605.718735 | -612.845228 |
| Eactivation of exo reaction | 0.043153
(27.078896 kcal mol-1) |
0.0292695
(18.366875 kcal mol-1) |
(Do you have the log files for these calculations? This is an interesting result as endo still comes out as the thermodynamically favoured product at B3LYP/6-31G(d) for me Tam10 (talk) 13:57, 24 February 2016 (UTC))
Further Discussion
One major effect is the side reactions of diene which leads to undesired product, such as [4s+2s] dimerisation. Figure 9 shows the possible dimerisation TS of 1,4-butadiene. Corresponding Eact are calculated in the same manner as above. The result indicates that Eact of dimerisation is much higher than that of prototypical cycloaddition, hence the side reaction is an unlikely situation unless strong driving force is applied, e.g. high concentration of butadiene, or heating. Solvent is another factor to consider that contributes to endo:exo ratios. For example, endo product will be significantly favoured under polar environment. According to the kinetics, endo TS involves secondary overlap that could be stabilised by interacting with polar solvent, resulting in more achievable kinetic product. [8]
(This is a nice bit of further work. Would be good to see some further development (kinetics/thermodynamics) Tam10 (talk) 13:57, 24 February 2016 (UTC))
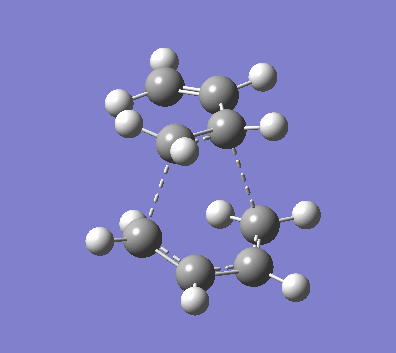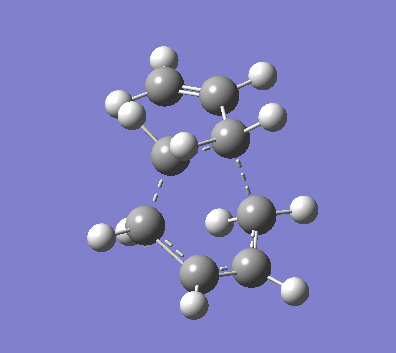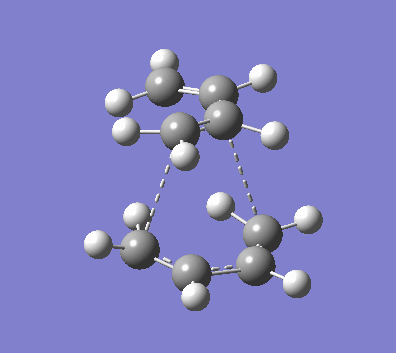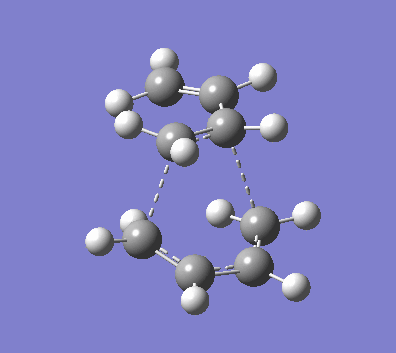
|
| Figure 9. TS vibration of undesired dimerisation reaction |
.
Conclusion
This study is base on the operation of Gaussian software. Molecules are mainly computed at HF/3-21G and B3LYP/6-31G(d) levels of theory, which provide slightly better optimisation than semi-empirical AM1. Besides optimisation and frequency jobs, TS(Berny) and QST2 options are used to propose TS of the reaction. IRC is also introduced for simulating chemical path. Reactions of Cope rearrangement and Diels-Alder cycloaddition are investigated by energy optimisation, MO analysis and computation of transition structure. Specifically, chair TS of Cope reaction is preferred over boat TS. Diels-Alder cycloaddition includes a prototypical (butadiene and ethene) and a reaction between maleic anhydrase and cyclobutadiene. The latter is for the purpose of regioselectivity study. Both reactions are able to behave as normal demand via [4s+2s] synchronised TS. Respect to regioselectivity, endo & exo TS geometries and relative energies are studied. Endo TS possess secondary orbital interaction therefore the lower electronic energy, but exo TS does not. Methods of higher resolution should be tried if time is allowed.
Reference
- ↑ 1.0 1.1 1.2 1.3 1.4 Gaussian 03 Revision, M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. A. Montgomery, Jr., etc, Gaussian, Inc., Wallingford CT, 2004.
- ↑ P.Atkins, J.D.Paula, Atkins' Physical Chemistry , 2010, 22, 852-856, Oxford Press
- ↑ Z. Zhou, B.W. Gung, R.A. Fouch, J.Am.Chem.Soc., 1995, 117, 1783-1788
- ↑ Robert N. Barnett, Uzi Landman, Phys. Rev. B, 1993, 48, 2081–2097
- ↑ Carey, Francis A., Richard J., Adv. Org. Chem. 5th Ed, New York, 2007, 836–850 ISBN 0387448993
- ↑ Marye A., James K. Organische Chemie: Grundlagen, Mechanismen, Bioorganische Anwendungen Springer, 1995 ISBN 978-3-86025-249-9.
- ↑ Bondi A., J. Phys. Chem., 1964, 68, 441-451 doi:10.1021/j100785a001
- ↑ 8.0 8.1 8.2 8.3 Ian Fleming, Molecular Orbitals and Organic Chemical Reactions, 2010, 6, 295-316