User:Xz9215
NH3 molecule

Bond length=1.01798A
Bond angle=105.74116°
Calculation Method: B3LYP
Basis set: 6-31G(d,p)
Final energy E(RB3LYP):-56.55776873au
Symmetry: C3v
Item Value Threshold Converged?
Maximum Force 0.000004 0.000450 YES
RMS Force 0.000004 0.000300 YES
Maximum Displacement 0.000072 0.001800 YES
RMS Displacement 0.000035 0.001200 YES
Predicted change in Energy=-5.986276D-10
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.018 -DE/DX = 0.0 !
! R2 R(1,3) 1.018 -DE/DX = 0.0 !
! R3 R(1,4) 1.018 -DE/DX = 0.0 !
! A1 A(2,1,3) 105.7412 -DE/DX = 0.0 !
! A2 A(2,1,4) 105.7412 -DE/DX = 0.0 !
! A3 A(3,1,4) 105.7412 -DE/DX = 0.0 !
! D1 D(2,1,4,3) -111.8571 -DE/DX = 0.0 !
ammonia molecule |
Vibrational analysis
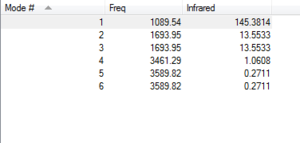
The vibrational modes are shown on the right.
NH3 has 6 vibrational modes according from the 3N-6 rule.
The second mode and the third mode have the same energy, while the fifth and the sixth mode also generate the same energy. Those modes are recognised as degenerated modes.
Mode 1,2,3 are "bending" vibrations and mode 4,5,6 are "bond stretch" vibrations.
Within those modes, the fourth mode is highly symmetric as the bonds all stretches at the same trend.
The first mode is known as the "umbrella" mode, because it bends into and out of the screen, just like the operation of an umbrella.
We are expected to see 2 bands of gaseous ammonia in experimental spectrum.
There is no negative frequency,so no transition state
Charges on NH3 molecule
Charge on N atom=-1.125
Charge on H atom=0.375
We expected to see negative charges on nitrogen atom and positive charge on hydrogen atom due to higher electronegativity of nitrogen.
Haber-Bosch process
Haber-Bosch process is an artificial nitrogen fixation process and is the main industrial procedure for the production of ammonia today.[1] It is named after its inventors, the German chemists Fritz Haber and Carl Bosch, who developed it in the first half of the 20th century. The process converts atmospheric nitrogen (N2) to ammonia (NH3) by a reaction with hydrogen (H2) using a metal catalyst under high temperatures and pressures. The following equation shows how the process proceed:
N2 + 3 H2 → 2 NH3
N2 molecule
Bond length=1.1055A
Bond angle=180°
Calculation Method: B3LYP
Basis set: 6-31G(d,p)
Final energy E(RB3LYP):-109.52412868au
Symmetry:D∞h
Item Value Threshold Converged?
Maximum Force 0.000001 0.000450 YES
RMS Force 0.000001 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000000 0.001200 YES
Predicted change in Energy=-3.400988D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.1055 -DE/DX = 0.0 !
--------------------------------------------------------------------------------
Vibrational analysis
Vibrational mode=1
frequency=2457.33Hz
No negative frequency,so no transition state
H2 molecule
Bond length=0.74279A
Bond angle=180°
Calculation Method: B3LYP
Basis set: 6-31G(d,p)
Final energy E(RB3LYP):-1.17853936au
Symmetry:D∞h
Item Value Threshold Converged?
Maximum Force 0.000000 0.000450 YES
RMS Force 0.000000 0.000300 YES
Maximum Displacement 0.000000 0.001800 YES
RMS Displacement 0.000001 0.001200 YES
Predicted change in Energy=-1.164080D-13
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.7428 -DE/DX = 0.0 !
Vibrational analysis
Vibrational mode=1
frequency=4465.68Hz
No negative frequency,so no transition state
Energy for Haber-Bosch process
E(NH3)=-56.55776873au
2*E(NH3)=-113.11553746au
E(N2)=-109.52412868au
E(H2)=-1.17853936au
3*E(H2)=-3.53561808au
ΔE=2*E(NH3)-[E(N2)+3*E(H2)]=-0.0557907au=-146.5 kJ·mol-1
As the energy released by nitrogen gas is much more than ammonia product, gaseous nitrogen is more stable than ammonia product.
Literature energy=-92.4 kJ·mol-1
he value calculated is quite different from the literature value, so this might not be a good method to calculate the final reaction energy of nitrogen and hydrogen.
H2O molecule
Bond length=0.96522 A
Bond angle=103.74544°
Calculation Method: B3LYP
Basis set: 6-31G(d,p)
Final energy E(RB3LYP):-76.41973740au
Symmetry: C2v
Literature value: The O-H bond lengths in the water molecule are 0.96 A, and the H-O-H angle is 104.5O°.
Item Value Threshold Converged?
Maximum Force 0.000099 0.000450 YES
RMS Force 0.000081 0.000300 YES
Maximum Displacement 0.000115 0.001800 YES
RMS Displacement 0.000120 0.001200 YES
Predicted change in Energy=-1.939669D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 0.9652 -DE/DX = 0.0001 !
! R2 R(1,3) 0.9652 -DE/DX = 0.0001 !
! A1 A(2,1,3) 103.7454 -DE/DX = 0.0 !
water molecule |
vibrational analysis
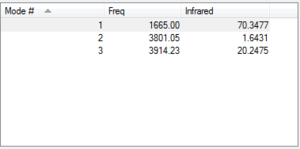
The vibrational modes are shown on the right.
Vibrational mode=3
Mode 1 is "bending" vibration and mode 2,3 are "bond stretch" vibrations.
Within those modes, the first and second mode is highly symmetric.
We should observe 3 bands in an experimental spectrum of water.
No negative frequency,so no transition state.
Charges on H2O molecule
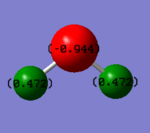
Charge on oxygen atom=-0.944
Charge on hydrogen atom=0.472
The figure of charged water molecule is shown on the right.
Molecular orbitals of H2O molecule



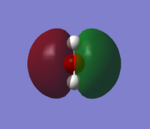

2S AO of oxygen and hydrogen σ MO contribute to the MO of water. It's a bonding orbital which is occupied, and this MO will form sigma bond between the atoms. Oxygen 2pz AO mix with this MO and lowers the orbital energy.
2py AO of oxygen and the hydrogen σ* MO gives the π bonding molecular orbital. It is occupied by one pair of electrons and will form Pi bond.
This bonding MO is formed from the mixing of the oxygen 2pz AO and the hydrogen σ MO. It is occupied and will form sigma bond. Oxygen 2s AO mix with bonding MO thus weakens bonding and raises the orbital energy.
This is a non-bonding MO from the oxygen 2px AO. Because the p-orbital is perpendicular to the molecular plane, thus it does not contribute to the bonding system. It is the HOMO of water. It is also occupied by two electrons and will form sigma bond between the atoms.
This anti-bonding orbital MO is formed from the mixing of the oxygen 2pz AO and the hydrogen σ MO. It is the LUMO of water molecule and it is unoccupied.
water formation from hydrogen and oxygen
The chemical equation of water formation is shown below:
O2 + 2 H2 → 2 H2O
O2 molecule
Bond length=1.1616 A
Bond angle=180°
Calculation Method: B3LYP
Basis set: 6-31G(d,p)
Final energy E(RB3LYP):-150.25742434au
Symmetry: C2v
Item Value Threshold Converged?
Maximum Force 0.000130 0.000450 YES
RMS Force 0.000130 0.000300 YES
Maximum Displacement 0.000080 0.001800 YES
RMS Displacement 0.000113 0.001200 YES
Predicted change in Energy=-1.033738D-08
Optimization completed.
-- Stationary point found.
----------------------------
! Optimized Parameters !
! (Angstroms and Degrees) !
-------------------------- --------------------------
! Name Definition Value Derivative Info. !
--------------------------------------------------------------------------------
! R1 R(1,2) 1.216 -DE/DX = -0.0001 !
Vibrational analysis
Vibrational mode=1
frequency=1642.74Hz
No negative frequency,so no transition state
Energy for water formation
E(H2)=-1.17853936au
2*E(H2)=-2.35707872au
E(O2)=-150.25742434au
E(H2O)=-76.41973740au
2*E(H2O)=-152.83947480au
ΔE=2*E(H2O)-[E(O2)+2*E(H2)]=-0.22497174au=-590.66 kJ·mol-1
Literature enthalpy=−285.8kJ·mol-1
The value calculated is very different from the literature value, so this might not be a good method to calculate the enthalpy of water formation.
