User:Xx108(module 3)

Module 3

Cope rearrangement

Cope rearrangement is a [3,3] sigmatropic pericyclic reaction. It involves the movement of a group from one place to another within a conjugated system. This is a concerted process during which one sigma bond is formed and one sigma bond is broken. In this section, the cope rearrangement of 1,5-hexadiene is investigated in order to study the chemical reactivity with the use of Gaussview.

Optimisation of reactants and products

Various conformers of 1,5-hexadiene

The log file for the optimised structure of anti1 can be found here: https://wiki.ch.ic.ac.uk/wiki/images/6/60/XiangXueREACT_ANTI1.LOG

The log file for the optimised structure of anti2 can be found here: https://wiki.ch.ic.ac.uk/wiki/images/b/b1/XiangXueREACT_ANTI2.LOG

The log file for the optimised structure of anti3 can be found here: https://wiki.ch.ic.ac.uk/wiki/images/9/93/XiangXueREACT_ANTI3.LOG

The log file for the optimised structure of gauche1 can be found here: https://wiki.ch.ic.ac.uk/wiki/images/9/97/XiangXueREACT_GAUCHE1.LOG

The log file for the optimised structure of gauche3 can be found here: https://wiki.ch.ic.ac.uk/wiki/images/1/15/XiangXueREACT_GAUCHE3.LOG

The log file for the optimised structure of gauche4 can be found here: https://wiki.ch.ic.ac.uk/wiki/images/7/73/XiangXueREACT_GAUCHE4.LOG

Geometry optimisation of different conformers

conformer	structure	point group	energy / Hartrees,HF/3-21G
anti1	Vibration	C2	-231.69260
anti2	Vibration	Ci	-231.69254
anti3	Vibration	C2h	-231.68907
gauche1	Vibration	C2	-231.68772
gauche3	Vibration	C1	-231.69266
gauche4	Vibration	C2	-231.69153

For a gauche conformer, the atoms are closer to each other compared to those in an anti conformer, this will lead to a larger steric repulsion in the gauche conformer, making it less stable. However,this is not consistent with the results obtained based on my calculation. From the above table, it can be seen that gauche3 conformer is the most stable one since its total energy is most negative. Therefore, the gauche conformer is found to be more stable than the anti one. This is because of the stereoelectronic reason which refers to the interaction between the pi-electrons of C=C and the vinyl proton in the gauche conformer. This is also known as the CH-pi interaction and it stabilises the gauche form.

The structures, energies and point groups for different conformers match well with those in Appendix 1.

Optimisation results of anti2 conformer using different methods

The log file for anti2 conformer using HF/3-21G method can be found here: https://wiki.ch.ic.ac.uk/wiki/images/b/b1/XiangXueREACT_ANTI2.LOG

The log file for anti2 conformer using B3LYP/6-31G method can be found here: https://wiki.ch.ic.ac.uk/wiki/images/b/b6/XiangXueREACT_ANTI2REOPTIMISED.LOG

Calculation method	HF/3-21G	B3LYP/6-31G
Labelled structure after optimisation
Energy / Hartrees	-231.69254	-234.61170
Point group	Ci	Ci
C1=C2 & C12=C13 bond lengths / A	1.32	1.33
C2-C6 & C9-C12 bond lengths / A	1.51	1.50
C6-C9 bond length / A	1.55	1.55
C1-C2-C6-C9 dihedral angle / 0	114.6	118.5
C2-C6-C9-C12 dihedral angle / 0	180.0	180.0
C6-C9-C12-C13 dihedral angle / 0	-114.6	-118.5

The energy of the optimised structure according to the B3LYP/6-31G method is little bit lower(3 Hartrees) compared to that based on the HF/3-21G method. The C-C bond lengths are almost the same in both cases. The dihedral angles at the terminal of the carbon chain differ by about 4⁰ while the C2-C6-C9-C12 dihedral angles are both 180.0⁰. As a result, the geometries obtained using these two methods are quite similar.

Thermochemistry of anti2 conformer

The D-space link for the frequency analysis of anti2 conformer at 298.15K can be found here: DOI:10042/to-10103

The D-space link for the frequency analysis of anti2 conformer at 0K can be found here: DOI:10042/to-10106

Energies calculated at different temperatures using B3LYP/6-31G method

	T=298.15K	T=0K
sum of electronic and zero-point energies / Hartrees	-234.46921	-234.46626
sum of electronic and thermal energies / Hartrees	-234.46186	-234.46068
sum of electronic and thermal enthalpies / Hartrees	-234.46091	-234.45973
sum of electronic and thermal free energies / Hartrees	-234.50082	-234.49551

The energy of the anti conformer at 0K is found to be higher than that at 298.15K. This is because more heat energy is absorbed by the molecule at a higher temperature, resulting in an increase in the thermal part of the total energy.

Optimisation of chair and boat transition state structures

Chair transition state

The log file for the optimisation of chair transition state using TS Berny method: https://wiki.ch.ic.ac.uk/wiki/images/e/ef/CHAIR_TS_OPTFREQ.LOG

The log file for the optimisation of chair transition state using Redundant coordinate method: https://wiki.ch.ic.ac.uk/wiki/images/6/61/CHAIR_TS_OPT2PART2MODIFIED.LOG

Optimised structure of chair transition state using different methods

	TS Berny method	Redundant coordinate method
optimised structure	Vibration	Vibration
energy / Hartrees	-231.61932	-231.61932
bond breaking bond length / A	2.02	2.02
bond forming bond length / A	2.02	2.02
imaginary frequency / cm-1	-818	-818
vibrational motion

The results from two methods are the same, indicating that both of them are valid in solving this problem. The imaginary frequency at -818cm^-1 corresponds to the process during with the bonds form and break simultaneously. This is in good agreement with the concerted mechanism found in the Cope rearrangement reaction and it is also confirmed by the vibrational motion images shown above.

It is worth noting that for a more complex molecule, the TS Berny method may not be appropriate. In such a case, the Redundant coordinate method has to be employed in order to obtain good results.

Boat transition state

The log file for the optimisation of boat transition state: https://wiki.ch.ic.ac.uk/wiki/images/8/82/BOAT_TS_OPTIMISEDMODIFIED.LOG

Optimised structure of boat transition state

	QST2 method
optimised structure	Vibration
energy / Hartrees	-231.60280
bond breaking bond length / A	2.14
bond forming bond length / A	2.14
imaginary frequency / cm-1	-840
vibrational motion

The imaginary frequency at -840cm^-1 again refers to the concerted bond forming and breaking process. This match well with the mechanism involved in Cope rearrangement and it is indicated by the vibrationa motion image as well.

By comparing the energies after optimisation for both chair and boat transition states, it can be found that the chair transition state is more stable(lower in energy). This is mainly due to the fact that the boat transition state structure is eclipsed while the chair transition state structure is staggered, leading to a smaller steric repulsion in the chair transition state.

IRC calculation for the chair transition state

The D-space link for the IRC calculation using 50 points and calculating force constant once: DOI:10042/to-10138

The D-space link for the IRC calculation using 50 points and calculating force constant always: DOI:10042/to-10139

Comparison of IRC ccalculation results using different methods

method	1: 50 points used, force constant calculated once	2: 50 points used, force constant calculated always
energy / Hartrees	-231.68524	-231.69166
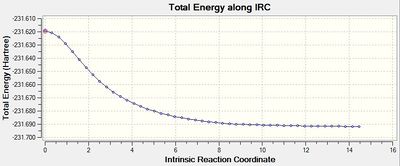
total energy along IRC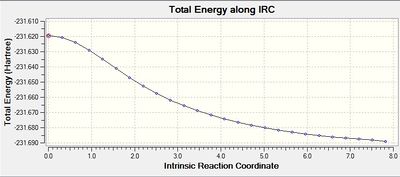
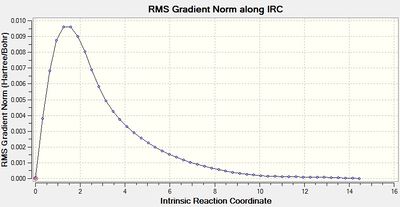
RMS gradient along IRC
structure obtained

For the 1st method, from the last few points on the energy graph, it can be seen that the energy is still decreasing so the minimum geometry has not been achieved. This is also confirmed by the gradient graph since the gradient does not go to 0. For the 2nd method, the last few points from the energy graph form a plateau. This implies that the minimum geometry has been obtained and it is further approved by the gradient graph as the gradient now reaches 0.

The optimised structure match well with that of gauche2 conformer shown in Appendix 1. Their energies are almost the same(-231.69166 vs -231.69167).

Activation energies via both transition states

The D-space link for the chair transition state structure at the B3LYP/6-31G level of theory: DOI:10042/to-10155

The D-space link for the boat transition state structure at the B3LYP/6-31G level of theory: DOI:10042/to-10156

Activation energies at the HF/3-21G level of theory

	electronic energy / Hartrees	sum of elctronic and zero-point energies at 0 K / Hartrees	sum of electronic and thermal energies at 298.15 K / Hartrees	Ea at 0 K / Hartrees	Ea at 298.15 K / Hartrees	Ea at 0 K / kcalmol-1	Ea at 298.15 K / kcalmol-1	Experimental Ea at 0 K / kcalmol-1
reactant	-231.69254	-231.53492	-231.53257	-	-	-	-	-
chair TS	-231.61932	-231.46638	-231.46135	0.07283	0.07122	45.70	44.69	33.5 ± 0.5
boat TS	-231.60280	-231.45071	-231.44530	0.08862	0.08727	55.61	54.76	44.7 ± 2.0

Activation energies at the B3LYP/6-31G level of theory

	electronic energy / Hartrees	sum of elctronic and zero-point energies at 0K / Hartrees	sum of electronic and thermal energies at 298.15K / Hartrees	Ea at 0K / Hartrees	Ea at 298.15K / Hartrees	Ea at 0 K / kcalmol-1	Ea at 298.15 K / kcalmol-1	Experimental Ea at 0 K / kcalmol-1
reactant	-234.61171	-234.46901	-234.46186	-	-	-	-	-
chair TS	-234.55698	-234.41465	-234.40900	0.05426	0.05286	34.05	33.17	33.5 ± 0.5
boat TS	-234.54309	-234.40217	-234.39601	0.06688	0.06585	41.97	41.32	44.7 ± 2.0

At 0K, E_a values are calculated as the difference between the sum of electronic and zero-point energies for both the reactant and the corresponding transition state. At 298.15K, E_a values are calculated as the difference between the sum of electronic and thermal energies for the reactant and the appropriate transition state. Since 1 Hartree = 627.509 kcal/mol, the units of E_a values are then converted to kcal/mol and compared with the experimental values.

At the HF/3-21G level of theory, the E_a values obtained at 0K are larger than the experimental values. While at the B3LYP/6-31G level of theory, the E_a values obtained at 0K are found to be in good agreement with the experimental values. This is because 6-31G is a larger basis set compared with 3-21G, which provides us with more accurate and reliable results.

From the above, it can be discovered that the chair transition state has a lower E_a value compared to the boat transition state. This is due to the fact that the chair transition state has a staggered conformation whereas the boat tranisition state has an eclipsed conformation, resulting in a smaller tortional strain in the chair transition state hence making it more stable. Therefore, the energy barrier for the Cope rearrangement reaction will be lower if it proceeds via a chair transition state.

Diels-Alder cycloaddition

Diels-Alder reaction is a [4+2] pericyclic reaction. It involves the concerted formation of 2 sigma bonds between the termini of a diene and a dienophile. In this part, two Diels-Alder reactions will be examined. The 1st one is the reaction between cis-butadiene and ethylene and the 2nd one is the reaction between maleic anhydride and 1,3-cyclohexadiene.

The reaction between cis-butadiene and ethylene

Geometry optimisation and molecular orbitals of reactants

The log file for the optimised structure of cis-butadiene: https://wiki.ch.ic.ac.uk/wiki/images/c/cb/CISBUTADIENEOPT.LOG

The log file for the optimised structure of ethylene: https://wiki.ch.ic.ac.uk/wiki/images/d/df/ETHYLENEOPT.LOG

Results obtained for the 2 reactants using the semi-empirical/AM1 method

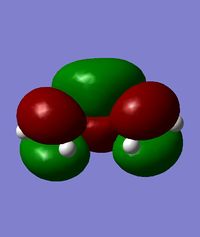
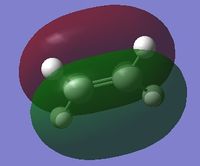
	HOMO of cis-butadiene	LUMO of cis-butadiene	HOMO of ethylene	LUMO of ethylene
orbital image
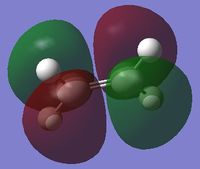
symmetry	anti-symmetric	symmetric	symmetric	anti-symmetric
energy / Hartrees	-0.34382	0.01709	-0.38777	0.05284

From the above, it can be observed that the HOMO of cis-butadiene and the LUMO of ethylene are both anti-symmetric while the LUMO of cis-butadiene and the HOMO of ethylene are both symmetric. Since the HOMO of one reactant has the same symmetry as the LUMO of the other reactant, it is very likely that these molecular orbitals will interact with each other, leading to a chemical reaction. This Diels-Alder reaction can happen provided that there is a significant orbital overlap.

Structural optimisation of the transition state

The log file for the optimised transition state structure using the Redundant/Frozen coordinate method: https://wiki.ch.ic.ac.uk/wiki/images/3/3d/DIELS_TS_OPTIMISED.LOG

Optimised structure of the transition state

method employed	Redundant/Frozen coordinate method
optimised structure	Vibration
energy / Hartrees	0.11166
bond breaking bond length / A	2.12
bond forming bond length / A	2.12
imaginary frequency / cm-1	-956

3 main computational methods are available for a transition state optimisation. They are TS Berny method, Redundant/Frozen coordinate method and QST2 method. The TS Berny method, though being considered as the easiest one, it may not work if the guessed transiton state structure is far from the exact structure. The QST2 method has an advantage that it is fully automated, but it can often fail if the structures of reactants and products are not close to the transition state structure. As a consequence, the Redundant/Frozen coordinate method is chosen for this optimisation.

Based on the Redundant coordinate method, the breaking/forming bond distances are first frozen to 2.2A and the structure is optimised to a minimum. Afterwards, these 2 bonds are unfrozen and the structure is then optimised to a transition state. The imaginary freqency at -956cm^-1 shows that the transition state has been successfully obtained.

Molecular orbitals of transition state

	HOMO	LUMO
orbital image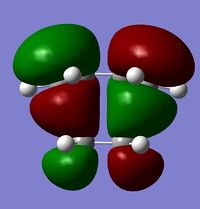
symmetry	anti-symmetric	symmetric
energy / Hartrees	-0.32394	0.02316

The HOMO of the transition state is found to be anti-symmetric. The HOMO of cis-butadiene and the LUMO of ethylene(both anti-symmetric) have been used to form this MO. Under thermal conditions, a pericyclic reaction with 4n+2 pi electrons will proceed via a Huckel transition state with all components suprafacial. For this cycloaddition reaction, 6 pi electrons are involved, indicating that it obeys the 4n+2 rule(n=1). In addition, the 2 new bonds are formed on the same face of cis-butadiene and ethylene pi systems, which shows that the components are indeed suprafacial. The reaction is therefore considered as allowed since it is consistent with the selection rule for pericylic reactions.

Geometry of transition state structure

Labelled structure after optimisation
C2-C1 & C4-C3 bond lengths / A	1.38
C1-C4 bond length / A	1.40
C3-C9 & C12-C2 bond lengths / A	2.12
C9-C12 bond length / A	1.39
C2-C1-C4 & C1-C4-C3 bond angles / 0	121.2
C4-C3-C9 & C12-C2-C1 bond angles / 0	99.3
C3-C9-C12 & C9-C12-C2 bond angles / 0	109.9

According to the literature values, the typical sp³ C-C bond length is 1.54A, the typical sp² C-C bond length is 1.48A and the van der Waals radius of the C atom is 1.70A. The 2 partly formed sigma C-C bonds, corresponding to C3-C9 and C2-C12 bonds shown above, both have a bond length of 2.12A. As a result, these 2 bonds are shorter than twice the van der Waals radius of a C atom but longer compared to the typical sp³ C-C bond. This implies that these C-C bonds are still forming, the process has not been completed.

Vibrational analysis of transiton state

The log file for the vibrational analysis of transition state: https://wiki.ch.ic.ac.uk/wiki/images/9/91/DIELS_TS_FREQ.LOG

Key vibrational frequencies summarised for the transition state

	vibrational mode	description of vibration	frequency / cm-1
mode 1		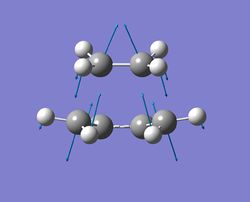The 2 terminal Cs of cis-butadiene unit move towards the 2 Cs of ethylene unit and vice versa, resulting in the synchronous formation of 2 sigma bonds.	-956
mode 2		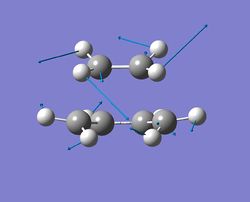Both cis-butadiene and ethylene units rock in the direction shown. The cis-butadiene unit moves with a smaller amplitude.	147

The vibration with frequency at -956cm^-1 refers to the reaction path at the transition state and it illustrates that the formation of 2 C-C sigma bonds is synchronous. For the vibration with the lowest positive frequency(147cm^-1), it is entirely different comapred to the vibration with the imaginary frequency. No bond forming/breaking process can be seen form this vibration.

Activation energy for this reaction

Activation energies at the semi-empirical/AM1 level of theory

	electronic energy / Hartrees	sum of electronic and thermal energies at 298.15 K / Hartrees	Ea at 298.15 K / Hartrees	Ea at 298.15 K / kcalmol-1	literature Ea at 298.15 K / kcalmol-1
cis-butadiene	0.04875	0.13952	-	-	-
ethylene	0.02621	0.08025	-	-	-
both reactants	0.07496	0.21977	-	-	-
TS	0.11163	0.25944	0.03967	24.69	27.5 ± 1.2

Activation energies at the B3LYP/6-31G level of theory

	electronic energy / Hartrees	sum of electronic and thermal energies at 298.15 K / Hartrees	Ea at 298.15 K / Hartrees	Ea at 298.15 K / kcalmol-1	literature Ea at 298.15 K / kcalmol-1
cis-butadiene	-155.68241	-155.93453	-	-	-
ethylene	-78.90022	-78.49528	-	-	-
both reactants	-234.58263	-234.42981	-	-	-
TS	-234.54720	-234.38794	0.04187	26.27	27.5 ± 1.2

At 298.15K, activation energy is the difference between the sum of electronic and thermal energies for both reactants and the transition state. As 1 Hartree = 627.509 kcal/mol, the unit of activtion energy is then converted to kcal/mol and compared with the literature.

At the semi-empirical/AM1 level of theory, the activation energy calculated at 298.15K is a little bit lower than the literature value. While at the B3LYP/6-31G level of theory, the activation energy obtained at 298.15K generally agrees with the literature. This is due to the fact that in the latter method a larger basis set in used, giving us a more accurate result.

The reaction between cyclohexa-1,3-diene and maleic anhydride

Structural optimisation for both exo and endo transition states

The log file for exo transition state at the semi-empirical/AM1 level of theory: not available here since the file size exceeds the upload limit on wiki page

The log file for endo transition state at the semi-empirical/AM1 level of theory: not available here since the file size exceeds the upload limit on wiki page

The D-space link for exo transition state at the B3LYP/6-31G level of theory: DOI:10042/to-10186

The D-space link for endo transition state at the B3LYP/6-31G level of theory: DOI:10042/to-10189

Optimised structure for both transition states at 2 different levels of theory using TS Berny method

	exo TS at the semi-empirical/AM1 level	exo TS at the B3LYP/6-31G level	endo TS at the semi-empirical/AM1 level	endo TS at the B3LYP/6-31G level
method employed	TS Berny	TS Berny	TS Berny	TS Berny
optimised structure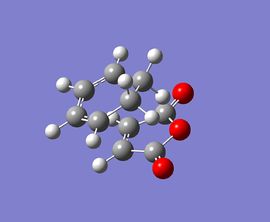
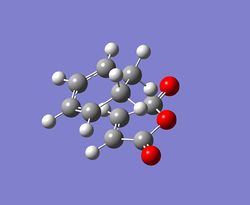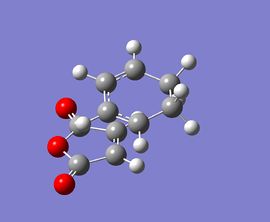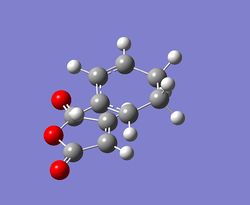
energy / Hartrees	-0.05044	-612.67931	-0.05153	-612.68339
bond breaking bond length / A	2.31	2.29	2.30	2.27
bond forming bond length / A	2.31	2.29	2.30	2.27
imaginary frequency / cm-1	-812	-448	-806	-447

At the beginning, both reactants(cyclohexa-1,3-diene and maleic anhydride) are optimised at the semi-empirical/AM1 level and then at the B3LYP/6-31G level. After that, the exo and endo transition states are optimised at those levels of theory with the use of TS Berny method. Finally, the results for the transition states are summarised and tablulated.

According to the calculations at both levels of theory, it can be found that the endo transition state is always more stable compared to the exo transition state since its total energy is lower. This also illustrates that the activation energy for the reaction will be lower if it proceeds via an endo transition state, resulting in the formation of a kinetic product. Furthermore, the imaginary frequencies in both cases indicate that the transition states have been successfully obtained.

Geometry for both transition states

Geometry for exo transition state at the B3LYP/6-31G level of theory

Labelled structure after optimisation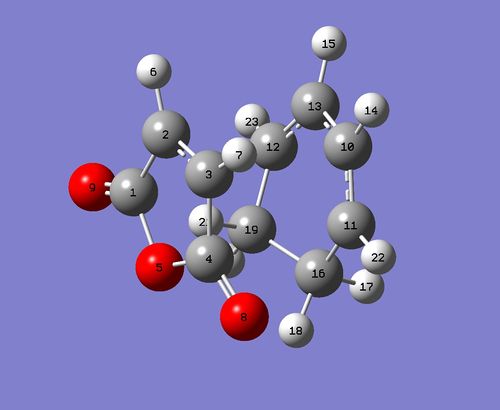
C2-C1 & C3-C4 bond lengths / A	1.48
C2-C3 bond length / A	1.40
C11-C10 & C12-C13 bond lengths / A	1.39
C10-C13 bond length / A	1.40
C12-C19 & C11-C16 bond lengths / A	1.51
C16-C19 bond length / A	1.56
C16-C4 & C19-C1 through space distances / A	3.03
C3-C11 & C2-C12 bond forming/breaking bond length / A	2.29

Geometry for endo transition state at the B3LYP/6-31G level of theory

Labelled structure after optimisation
C2-C1 & C3-C4 bond lengths / A	1.48
C2-C3 bond length / A	1.40
C11-C10 & C12-C13 bond lengths / A	1.39
C10-C13 bond length / A	1.40
C12-C19 & C11-C16 bond lengths / A	1.51
C16-C19 bond length / A	1.56
C13-C4 & C10-C1 through space distances / A	2.99
C2-C11 & C3-C12 bond forming/breaking bond length / A	2.27

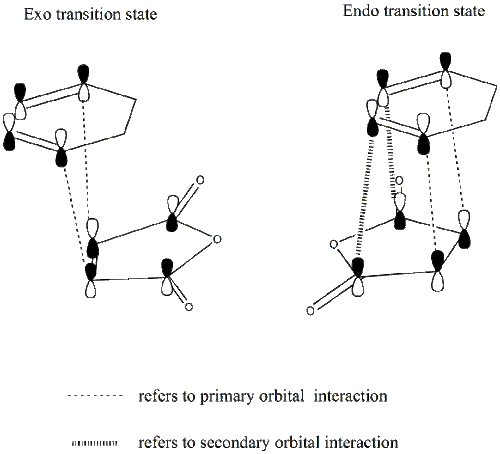
For both transition states, all the C-C bond lengths are the same except the bond forming/breaking bond lengths which differ by 0.02A. However, the C-C through space distances for the exo form(3.03A) are a little bit longer than those for the endo form(2.99A). From this, the endo form is expected to be less stable due to a larger steric repulsion. This contradicts with our energy calculations shown above where the endo form is found to be more stable. This is probably due to the fact that secondary orbital interactions are present in the endo transition structure which have not been taken into account so far. As a consequence, the molecular orbitals for both transition states need to be studied and this secondary orbital interaction will be discussed in detail in the following section.

Molecular orbitals for both transition states

Molecular orbitals for both transition states at the B3LYP/6-31G level of theory

	HOMO of exo transition state	LUMO of exo transition state	HOMO of endo transition state	LUMO of endo transition state
orbital image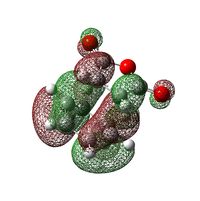
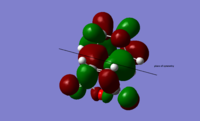symmetry	anti-symmetric	anti-symmetric	anti-symmetric	anti-symmetric
energy / Hartrees	-0.24215	-0.07841	-0.24231	-0.06774

The HOMO and LUMO for both transition states are found to be anti-symmetric. The HOMO for both transition states is made up of the HOMO of cyclohexa-1,3-diene and the LUMO of maleic anhydride, owing to the smaller HOMO-LUMO energy gap compared with that between the HOMO of maleic anhydride and the LUMO of cyclohexa-1,3-diene. In general, it is the interaction between the HOMO of the diene and the LUMO of the dienophile which gives rise to this Diel-Alder reaction.

From the diagram, it can be seen that both primary and secondary orbital interactions are present in the endo transition state whereas in the exo transition state, there is only primary orbital interaction. Secondary orbital interaction is essentially the orbital overlap between the pi systems of -CH=CH- and -(C=O)-O-(C=O)- fragments. This interaction is favourable in the endo transition state because the pi orbitals from both fragments are in the same phase and the spatial orientation is appropriate. For the exo transition state, the pi orbitals from the 2 fragments are far apart from each other due to spatial arrangement so secondary orbital interaction no longer exists.

Based on the HOMOs for the exo and endo transition states shown in the above table, in both cases, a nodal plane can be seen between the -(C=O)-O-(C=O)- fragment and the remainder of the system. For the endo form, the pi orbitals due to carbonyl carbons on the anhydride fragment are pointing out of the plane of the paper while for the exo form, those pi orbials stay within the plane. This again confirms that it is the spatial orientation of these orbitals which determines whether the secondary orbital interaction is possible or not.

In conclusion, the presence of secondary orbital interactions stabilises the endo transition state, leading to a reaction pathway with lower activation energy.

Limitations of computational methods and effects neglected during the calculations for Diels-Alder reactions

Computational methods such as Gaussian can be used to investigate the transition states of a pericyclic reaction. In this section, a Cope rearrangement and 2 Diels-Alder cycloaddition reactions have been studied and some conclusions have been drawn accordingly.

Although these computational methods give reasonably good results, there are some limitations. Gaussian calculation is not able to tell if the reaction is kinetically controlled or thermodynamically controlled. All the calculations are carried out based on the fact that the major product is already known to us. Furthermore, the degree of accuracy of the results obtained mainly depends on the level of theory used in the calculation. Therefore, a level of theory with a larger basis set could be introduced in order to improve the final results.

There are some important effects which need to be considered in these calculations as well. At first, the effect of high pressure on Diel-Alder reactions has been ignored. What's more, Diels-Alder reactions can take place under the condition of light. This has not been mentioned in this exercise, either.