Jump to content

User:Xx108(module 2)

From ChemWiki

Module 2


BH3 analysis

Geometry optimisation

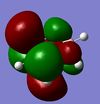
This is the structure of BH3 after optimisation:


Vibration


The log file of BH3 optimisation can be accessed here: https://wiki.ch.ic.ac.uk/wiki/images/8/85/BH3_OPTIMISATION.LOG


BH3 optimisation
File type .log
Calculation type FOPT
Calculation method RB3LYP
Basis set 3-21G
Charge 0
Spin Singlet
E(RB3LYP) -26.4623 a.u.
RMS gradient norm 0.0002 a.u.
Imaginary freq
Dipole moment 0.00 Debye
Point group D3h
H-B bond length 1.19 A
H-B-H bond angle 120.00


From the above, it can be seen that the H-B bond length of the optimised BH3 is 1.19A and the H-B-H bond angle is 120.00. These are consistent with the literature values[1] where the bond length is 1.21A and the bond angle is 120.00.


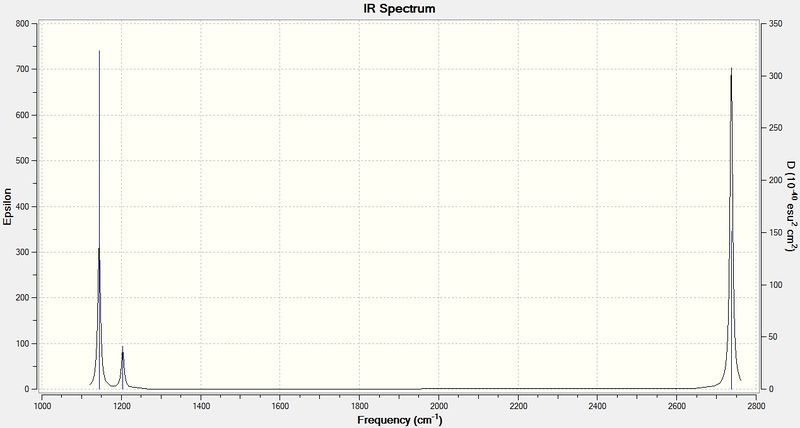
Vibrational/Frequency analysis

The log file of BH3 vibrational analysis can be accessed here: https://wiki.ch.ic.ac.uk/wiki/images/e/e0/XIANGXUE_BH3_FREQ.LOG


Vibrational analysis of BH3
No. Form of vibration Description of vibration Frequency/cm-1 Intensity Symmetry D3h point group Frequency in literature[2]/cm-1
1 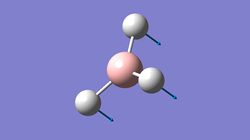All the H atoms move into and out of the BH3 plane simultaneously while the B atom moves in an opposite direction with a smaller amplitude. 1144 93 A2" 1159
2 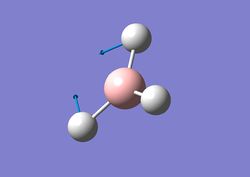Two H atoms move in a 'scissor-like' fashion while the B and remaining H atom move slightly in the opposite direction. 1204 12 E' 1202
3 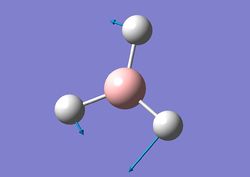Two H atoms and B rock together in the same plane while the other H moves sideways with a larger amplitude. 1204 12 E' 1202
4 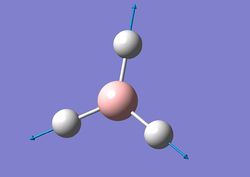All the H atoms move to and away from the B atom in the BH3 plane with the B atom remaining stationary. 2598 0 A1' -
5 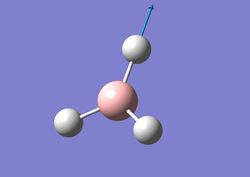1 H atom moves to B wihile the other moves away from B. B atom itself moves slightly and the 3rd H remains stationary during the entire process. 2737 104 E' 2616
6 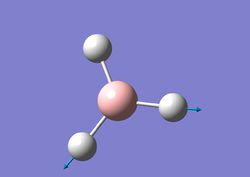Two H atoms move to and away from B at the same time while the 3rd H does the opposite(moves away from and then to B). Again the B atom moves with a very small amplitude. 2737 104 E' 2616



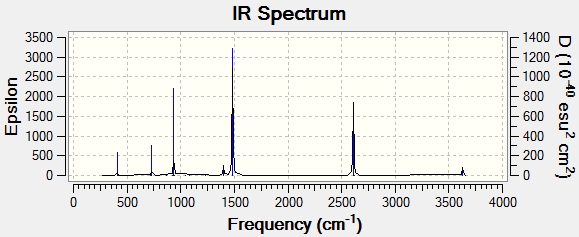
There are 6 forms of vibrations but only 3 peaks are seen in the IR spectrum. This is due to the fact that just 4 distinctive frequencies are present and one of these frequencies has an intensity of 0. The vibrational forms 2 and 3 are degenerate, showing 1 peak only in the IR spectrum. This applies to the vibrational forms 5 and 6 as well. What's more, vibrational form 4 is a kind of symmetric stretching hence leading to no change in dipole moment of the molecule. Since IR spectrum reflects the change in dipole moment of a vibration, vibrational form 4 is not detected.


The frequencies obtained from my calcuation are close to those in literature which indicates that my result is reasonably good.


Population analysis and MO digram of BH3

The data obtained from NBO/population analysis(D-space link)can be accessed here: DOI:10042/to-9693



BH3 MO.gif


From the above MO digram, it can be seen that the shapes of the calculated MOs are very similar to those produced by qualitative MO theory. The energy levels from calculation are generally in good agreement with those in MO theory, too. The only exception is that the orbitals with symmetry label 2e' are higher in energy than that with symmetry label 3a1' according to our 2nd year MO course. This indicates the limitation of qualitative MO theory. In other words, the energy levels of MOs can not be accurately predicted by qualitative MO theory. In order to work out the exact energy levels, a calculation has to be performed.


It is also worth noting that here my Gaussian calculations are carried out based on a basis set of 3-21G. If a larger basis set like 6-311G(d,p) is used, the relative order of energy levels for 2e' and 3a1' orbitals will be reversed. The latter one is more reliable in this case since a larger basis set is used(give a more accurate result), but it again shows that the 2e' and 3a1' orbitals are very close in energy so it can't be determined by qualitative MO theory.


TlBr3 analysis

Geometry optimisation

This is the structure of TlBr3 after optimisation:


Vibration


The log file of TlBr3 optimisation can be accessed here: https://wiki.ch.ic.ac.uk/wiki/images/5/53/TLBR3_OPTIMISATIO.LOG


TlBr3 optimisation
File type .log
Calculation type FOPT
Calculation method RB3LYP
Basis set LANL2DZ
Charge 0
Spin Singlet
E(RB3LYP) -91.2181 a.u.
RMS gradient norm 0.0000 a.u.
Imaginary freq
Dipole moment 0.00 Debye
Point group D3h
Br-Tl bond length 2.65 A
Br-Tl-Br bond angle 120.00


The calculation method used is DFT-B3LYP with a basis set called LANL2DZ(pseudo potential). The larger basis set LANL2DZ is introduced because now we are dealing with heavy atoms in our molecule. As a pseudo potential can model effects which are considered to be important for heavier atoms, it will provide us with better results.


The Br-Tl bond length of the optimised TlBr3 is 2.65A and the Br-Tl-Br bond angle is 120.00. These generally agree with the literature[3] where the bond length is 2.51A and the bond angle is 120.00.


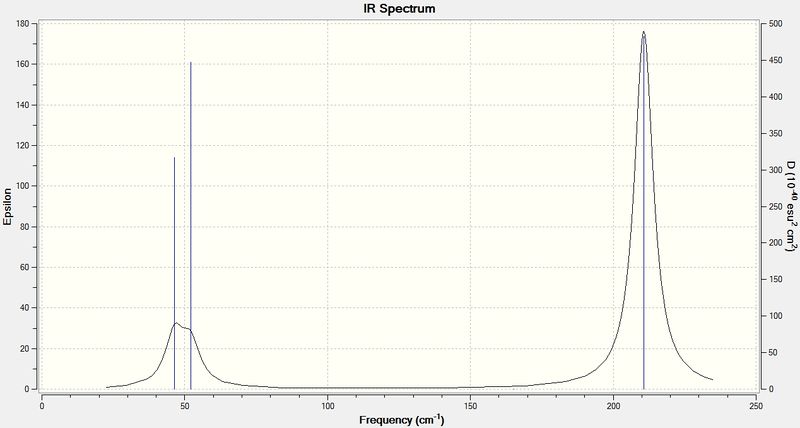
Vibrational/Frequency analysis

The log file of TlBr3 vibrational analysis can be accessed here: https://wiki.ch.ic.ac.uk/wiki/images/b/b8/XIANGXUE_TLBR3_FREQ.LOG


Vibrational/Frequency analysis of TlBr3
No. Form of vibration Description of vibration Frequency/cm-1 Intensity Symmetry D3h point group Frequency in literature[4]/cm-1
1 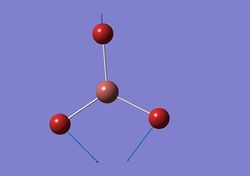Two H atoms move in a 'scissor-like' fashion while the B and remaining H atom move slightly in the opposite direction. 46 4 E' -
2 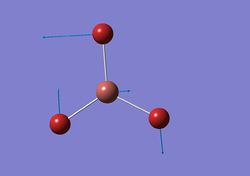Two H atoms and B rock together in the same plane while the other H moves sideways with a larger amplitude. 46 4 E' -
3 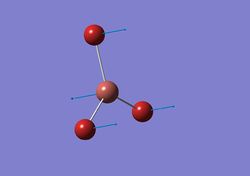All the H atoms move into and out of the BH3 plane simultaneously while the B atom moves in an opposite direction. 52 6 A2" -
4 All the H atoms move to and away from the B atom in the BH3 plane with the B atom remaining stationary. 165 0 A1' 190
5 1 H atom moves to B wihile the other moves away from B. B atom itself moves slightly and the 3rd H remains stationary during the entire process. 211 25 E' 202
6 Two H atoms move to and away from B at the same time while the 3rd H does the opposite(moves away from and then to B). Again the B atom moves with a smaller amplitude. 211 25 E' 202



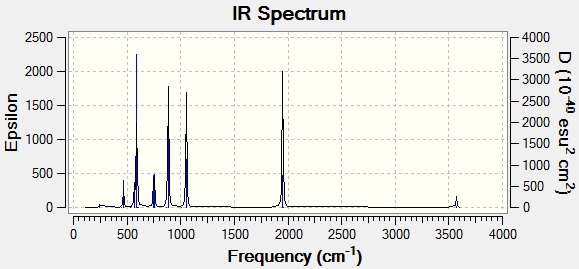
A frequency analysis needs to be carried out in order to determine wheter the optimised structure has a minimum energy or not. During the geometry optimisation process, the 1st derivative of the energy optimisation is set to 0. From a mathematical point of view, this could give us a structure with either a maximum or a minimum energy. As a consequence, the frequency analysis, which refers to the 2nd derivative of the energy optimisation, has to be performed. Values obtained from frequency analysis should be positive if the optimised structure has a minimum energy.


For both the geometry optimisation and frequency analysis, the same method and basis set has to be used. This is because the results from both parts need to be consistent. Different methods or basis sets will produce entirely different results which are not comparable at all.


According to the data in the log file, the low freqencies for TlBr3 are 4cm-1,4cm-1,0cm-1,0cm-1,0cm-1 and -3cm-1 respectively. The lowest real normal mode is found to be 46cm-1.


Answers regarding chemical bonds

Generally speaking, a bond is an electrostatic attraction between two oppositely charged species(ions,atoms,etc.)which results in the formation of a chemical compound. There are strong bonds like ionic bonds, metallic bonds and covalent bonds. There are also weak bonds such as hydrogen bonds, dipole-dipole interactions and so on. For computer programs like Gaussview, it has a certain range of values for a chemical bond. If the bond length between two atoms goes beyond that range, it will no longer be considered as a bond by Gaussview so no bond is shown. In such a situation, it doesn't mean that there is no bond between the atoms, it is just not drawn by Gaussview. For organic compounds, this is fine since most of the bonds fall within the range of Gaussview. For inorganic compounds, bonds are usually found to be longer than those in organic molecules. As a result, this kind of problem arises.


Mo(CO)4(PCl3)2 analysis

Geometry optimisation

The D-space link for cis-isomer after 1st optimisation can be accessed here: DOI:10042/to-9697

The D-space link for trans-isomer after 1st optimisation can be accessed here: DOI:10042/to-9698


1st geometry optimisation for both isomers of Mo(CO)4(PCl3)2
cis-isomer trans-isomer
File type .log .log
Calculation type FOPT FOPT
Calculation method RB3LYP RB3LYP
Basis set LANL2MB LANL2MB
Charge 0 0
Spin Singlet Singlet
E(RB3LYP) -617.5250 a.u. -617.5220 a.u.
RMS gradient norm 0.0000 a.u. 0.0001 a.u.
Imaginary freq
Dipole moment 8.46 Debye 0.00 Debye
Point group C1 C1


The D-space link for cis-isomer after 2nd optimisation can be accessed here: DOI:10042/to-9701

The D-space link for trans-isomer after 2nd optimisation can be accessed here: DOI:10042/to-9702


2nd geometry optimisation for both isomers of Mo(CO)4(PCl3)2
cis-isomer trans-isomer
File type .log .log
Calculation type FOPT FOPT
Calculation method RB3LYP RB3LYP
Basis set LANL2DZ LANL2DZ
Charge 0 0
Spin Singlet Singlet
E(RB3LYP) -623.5771 a.u. -623.5760 a.u.
RMS gradient norm 0.0000 a.u. 0.0000 a.u.
Imaginary freq
Dipole moment 1.31 Debye 0.30 Debye
Point group C1 C1


Trans-isomer is the thermodynamic product whereas cis-isomer is the kinetic product[5]. There are two main reasons why trans-isomer is more stable. The 1st issue is steric hindrance. In trans-isomer, the two bulky PCl3 groups are far away from each other while in cis isomer the two PCl3 groups are relatively close. In this way, the trans-isomer is less sterically hindered, making the compound more stable. The 2nd issue is the overall dipole moment. In trans-isomer, due to the spatial arrangement of the substituents, the overall dipole moment is 0 because the dipole moments generated by different groups cancel out each other. In cis-isomer, the situation is different so the molecule now has an overall dipole moment. This again stabilises the trans-isomer.


Energy difference between two isomers = 623.5771 - 623.5760 = 0.0011 a.u., which is roughly 3kJ/mol. This is a very small energy difference so the trans/cis isomer interconversion process may occur quite easily. According to the energy values from the 2nd geometry optimisation table shown above, the cis-isomer is found to be more stable since its total energy is more negative. This implies that the basis sets that has been used for this calculation are not good enough . For example, a basis set that takes into account the low lying d atomic orbitals of P atoms may be introduced, which will definitely provide us with better results.


There are various ways to further stabilise the trans isomer. By the use of a more bulky ligand such as PPh3, the steric hindrance effect will be enhanced for cis isomer. Consequently the formation of trans isomer will be more favourable. In addition, if a more electronegative group like F is introduced to replace Cl, the overall dipole moment for cis isomer will be increased. Since the overall dipole moment for trans isomer is always 0, it will be more stable compared to the cis isomer.


Comparison of bond lengths and bond angles for the trans isomer with those in literature
P-Mo bond length C-Mo bond length P-Cl/P-C bond length C-O bond length P-Mo-P bond angle cis C-Mo-C bond angle trans C-Mo-C bond angle C-Mo-P bond angle
trans-Mo(CO)4(PCl3)2 2.44A 2.06A 2.24A 1.17A 177.20 89.40, 90.60, 91.30 178.40, 1800 91.30, 900, 88.70
literature value for trans-Mo(CO)4(PPh3)2 2.500A 2.005A 1.828A 1.164A 1800 92.10 1800 87.20


The results obtained from my calculation are a little bit different from those in literature[6]. This is probably because in literature the PPh3 ligand is present rather than the PCl3 ligand, which slightly distorts the structure of the compound. It could also suggest that the calculation method and basis set used are not very good. The introduction of a more appropriate calculation method or basis set may be necessary.


The structures for both isomers after 2nd optimisation can be seen here:


cis-isomer trans-isomer
Vibration
Vibration


Vibrational/Frequency analysis

The log file of cis Mo(CO)4(PCl3)2 vibrational analysis can be accessed here: DOI:10042/to-9733

The log file of trans Mo(CO)4(PCl3)2 vibrational analysis can be accessed here: DOI:10042/to-9734


Low vibrational frequencies summarised for cis and trans isomer
Form of vibration Description of vibration Frequency/cm-1 Intensity Symmetry C1 point group
cis isomer mode 1 Both PCl3 ligands rock together and they are out of phase in comparison with MO(CO)4. 11 0 A
cis isomer mode 2 The PCl3 and CO ligands rock out of phase in comparison with Mo,while Mo itself remains stationary. 18 0 A
trans isomer mode 1 Both PCl3 ligands rock in phase with each other, but they are out out phase in comparison with MO(CO)4. 5 0 A
trans isomer mode 2 Both PCl3 ligands rock out of phase with each other while Mo remains stationary. 6 0 A


These are the vibrations that have very low frequencies. Since energy is directly proportional to frequency, it means that the energy required for these vibrations to take place is very small. In other words, these vibrations may even take place at room temperature.


Carbonyl stretching frequencies for cis Mo(CO)4(PCl3)2
Frequency/cm-1 Intensity Frequency in literature[7]/cm-1 Symmetry label
1945 763 1986 B2
1949 1499 1994 B1
1958 633 2004 A1
2023 598 2072 A1
Carbonyl stretching frequencies for trans Mo(CO)4(PCl3)2
Frequency/cm-1 Intensity Frequency in literature[8]/cm-1 Symmetry label
1950 1475 1896 Eu
1951 1467 1896 Eu
1977 1 - B1g
2031 4 - A1g


For the cis isomer, there are 4 peaks from both my calculation and the IR spectrum(literature). The frequency values for all the 4 peaks are close to those in literature, too. For the trans isomer, 4 peaks are found based on my calculation but only 2 of them are observed on the IR spectrum. This is because 2 of the vibration modes don't lead to an overall change in dipole moment of the molecule, rendering them IR inactive. The frequency values for the 2 peaks which can be seen on the IR spectrum generally agree with those in literature.


Mini project: Comparison of structures for borazine(B3N3H6) and its analogue Al3N3H6

Introduction

Borazine(B3N3H6) has been discovered and studied for a long time. It is now generally accepted that it has a benzene-like structure with 6 delocalised pi electrons. In this project, both structures of borazine and its analogue Al3N3H6, will be investigated by carrying out a series of calculations(geometry optimisation, molecular orbital analysis etc.). By the end of the project, we should be able to tell whether Al3N3H6 has a structure similar to benzene or not.


Geometry optimisation

The structures of both compounds after optimisation can be seen here:


B3N3H6 Al3N3H6
Vibration
Vibration


The log file of B3N3H6 optimisation can be accessed here: DOI:10042/to-9852

The log file of Al3N3H6 optimisation can be accessed here: DOI:10042/to-9853


B3N3H6 optimisation
File type .log
Calculation type FOPT
Calculation method RB3LYP
Basis set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -242.7445 a.u.
RMS gradient norm 0.0001 a.u.
Imaginary freq
Dipole moment 0.00 Debye
Point group C1
B-H bond length 1.19 A
N-H bond length 1.01 A
N-B bond length 1.43 A
B-N-B bond angle 122.90
N-B-N bond angle 117.10
Al3N3H6 optimisation
File type .log
Calculation type FOPT
Calculation method RB3LYP
Basis set 6-311G(d,p)
Charge 0
Spin Singlet
E(RB3LYP) -895.5009 a.u.
RMS gradient norm 0.0001 a.u.
Imaginary freq
Dipole moment 0.00 Debye
Point group C1
Al-H bond length 1.58 A
N-H bond length 1.01 A
N-Al bond length 1.80 A
Al-N-Al bond angle 122.30
N-Al-N bond angle 117.70


Here the calculation method RB3LYP and the basis set 6-311G(d,p)are used. A large basis set like this is introduced so as to increase the accuracy in our results.


For the optimised structure of B3N3H6, the B-H, N-H and N-B bond lengths are 1.19A, 1.01A and 1.43A respectively. These are close to the literature values[9] where B-H bond length = 1.26A, N-H bond length = 1.05A and N-B bond length = 1.44A. The bond angles from calculation(122.90, 117.10) generally agrees with those found in literature, which are 120.00 in both situation.


For the optimised structure of Al3N3H6, the Al-H, N-H and N-Al bond lengths are found to be 1.58A, 1.01A and 1.80A respectively. These correspond well with the literature values[10], where Al-H bond length = 1.60A, N-H bond length = 1.05A and N-Al bond length = 1.80A. Again the bond angles(122.30, 117.70) match quite well with those in literature, which are 120.00 in both cases.


Acoording to the Jmol models shown above for the optimised structures of two compounds, it can be seen that both of them have a planar structure. The six bonds forming the ring are equal in length and the bond angle is roughly 1200. All of these are the same as those values found in the structure of benzene. Nevertheless, only after the electronic structures of both compounds have been examined can we determine whether they have an aromatic structure or not.


Vibrational/Frequency analysis

The log file of B3N3H6 vibrational analysis can be accessed here: DOI:10042/to-9868

The log file of Al3N3H6 vibrational analysis can be accessed here: DOI:10042/to-9869


Key vibrations obersved on the IR spectrum of B3N3H6
No. Form of vibration Frequency/cm-1 Intensity Frequency in literature[11]/cm-1
1 409 24 420
2 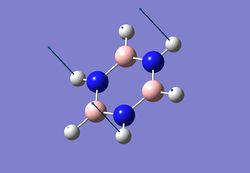731 55 745
3 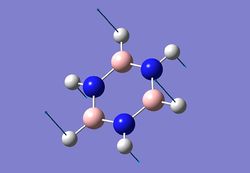936 206 951
4 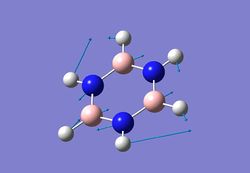1484 479 492
5 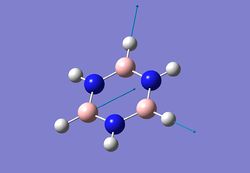2610 295 2633
6 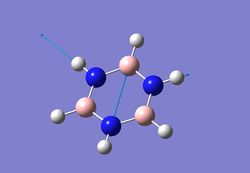3630 43 3647



Key vibrations obersved on the IR spectrum of Al3N3H6
No. Form of vibration Frequency/cm-1 Intensity Frequency in literature[12]/cm-1
1 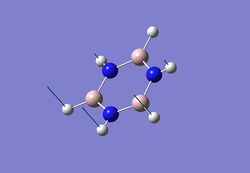469 73 484
2 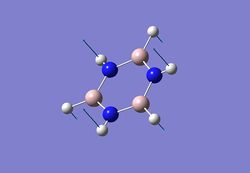590 533 -
3 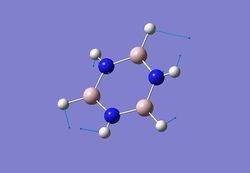751 145 -
4 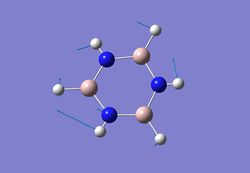883 354 -
5 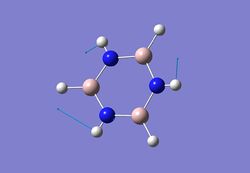1052 296 1061
6 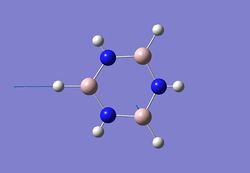1952 369 -
7 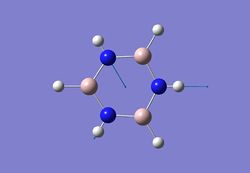3572 24 -



The purpose of doing a frequency analysis is to check if the geometry optimisation step is successful. During the process of geometry optimisation, the 1st derivative of energy optimisation is set to 0. This gives us an energy value which could either be a maximum or minimum. As a consequence, the 2nd derivative of energy optimisation, namely frequency analysis, needs to be performed.In this situation, since all frequency values calculated for both compounds are postivie(i.e. 2nd derivative is greater than 0), the minimum energy has been found.


Molecular orbital and NBO analysis

The log file of B3N3H6 molecular orbital analysis can be accessed here: DOI:10042/to-9856

The log file of Al3N3H6 molecular orbital analysis can be accessed here: DOI:10042/to-9857



Different MOs of B3N3H6 and Al3N3H6
LUMO+1 LUMO HOMO HOMO-1 HOMO-2 HOMO-3 HOMO-4
B3N3H6
Al3N3H6


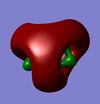
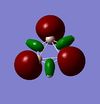
From the MO pictures of B3N3H6, pi electron delocalisation above and below the 6-membered ring can be clearly seen. This indicates that B3N3H6 has a benzene-lke structure with 6 pi electrons present. Therefore, the compound is aromatic and it should be reasonably stable.


From the MO pictures of Al3N3H6, the pi electron delocalisation pattern is not that obvious compared to that of B3N3H6, but it can stil be observed. This shows that Al3N3H6 also has a benzene-like structure with 6 pi electrons. However, the compound is less aromatic than B3N3H6 due to weaker pi electron delocalisation and it is less stable than borazine.


The above analysis has been approved by literature as well. B3N3H6 is isoelectronic with benzene. The 6 pi electons in the 6-membered ring is delocalised hence it shows some aromatic character[13]. Nevertheless, because of the difference in electronegativity between N and B, the degree of delocalisation in B3N3H6 is smaller compared to that in benzene where all the atoms forming the ring are identical. In the case of Al3N3H6, it has a delocalised ring wtih 6 pi electrons present which exhibits some aromaticity[14], too. Since the electronegativity difference between N and Al is even larger, the degree of delocalisation in Al3N3H6 is expected to be smaller than that in B3N3H6.


Aromaticity displayed : benzene > B3N3H6 > Al3N3H6



NBO analysis summarised for B3N3H6
N-B bond N-H bond B-H bond
charge distribution N atom: -0.340 B atom: 0.206 N atom: -0.340 H atom: 0.206 B atom: 0.206 H atom: -0.072
atomic contribution N atom: 75.74% B atom: 24.26% N atom: 70.14% H atom: 29.86% B atom: 45.23% H atom: 54.77%
orbital contribution N atom: 38.89% from s, 61.08% from p, 0.03% from d; B atom: 31.72% from s, 68.15% from p, 0.14% from d N atom: 22.10% from s, 77.85% from p, 0.05% from d; H atom: 99.94% from s, 0.06% from p B atom: 36.64% from s, 63.32% from p, 0.04% from d; H atom: 99.92% from s, 0.08% from p
NBO analysis summarised for Al3N3H6
N-Al bond N-H bond Al-H bond
charge distribution N atom: -0.914 Al atom: 0.881 N atom: -0.914 H atom: 0.238 Al atom: 0.881 H atom: -0.208
atomic contribution N atom: 88.15% Al atom: 11.85% N atom: 70.12% H atom: 29.88% Al atom: 29.20% H atom: 70.80%
orbital contribution N atom: 38.89% from s, 61.07% from p, 0.04% from d; Al atom: 33.26% from s, 65.54% from p, 0.02% from d N atom: 22.06% from s, 77.87% from p, 0.07% from d; H atom: 99.95% from s, 0.05% from p Al atom: 33.35% from s, 65.92% from p, 0.02% from d; H atom: 99.91% from s, 0.09% from p


In a covalent bond, 2 atoms share electrons with each other. However, the more electronegative atom draws electron density towards itself hence it becomes more negative compared to the other atom. In this way, it makes a larger contribution in forming the bond. This argument is well supported by the results from charge distribution and atomic contribution shown above. The more electronegative atom always has a negative charge and its percentage contribution to bond formation is larger.


The fact that B is more electronegative than Al is also justified by these results. For a N-B bond, B atom contributes about 24% while in the case of N-Al bond, Al atom just contributes 12%. As B contributes more in forming the bond, it is more electronegative than Al. This also explains the larger electronegativity difference in N-Al compared to that in N-B, resulting in Al3N3H6 being less aromatic than B3N3H6. In addition, from the orbital contribution data, it can be discovered that the d orbitals of N, B and Al are almost not used during bond formation. That is to say, our focus should be on s and p orbitals only.


Conclusion

Based on the calculations and interpretations provided, it can be concluded that Al3N3H6 indeed has a structure similar to benzene though it is far less aromatic than benzene.


References

  1. ↑ M. Hartman, J. Rush, T. Udovic, R. Bowman Jr, Solid State. Chem., 2007, 180, 1296 - 1306 DOI:10.1016/j.jssc.2007.01.031
  2. ↑ M.Schuurman, W.Allen, Comput. Chem., 2005, 26, 1106-1109 DOI:10.1002/jcc.20238
  3. ↑ H. Asadi, and E. Murashova, Inorganica Chimica Acta, 2009, 362, 2291-2298: DOI:10.1016/j.ica.2008.10.028
  4. ↑ G.Lewis, J. Am. Chem. Soc., 1916, 38, 762: DOI:10.1021/ja02261a002
  5. ↑ D. Darensbourg, Inorga. Chem., 1979, 18, 14 - 16 DOI:10.1021/ic50191a003
  6. ↑ G. Hogarth, T. Norman, Inorg. Chem, 1997, 254, 167-169. DOI:10.1016/S0020-1693(96)05133-X
  7. ↑ F. Cotton, Inorg. Chem., 1963, 3, 703 - 709 DOI:10.1021/ic50015a024
  8. ↑ F. Cotton, Inorg. Chem., 1963, 3, 703 - 709 DOI:10.1021/ic50015a024
  9. ↑ W. Harshbarger and R. Porter, Inorg. Chem., 1969, 1683–1689 DOI:10.1021/ic50078a023
  10. ↑ E. Jemmis and B. Kiran, Inorg. Chem., 1998, 2110–2114 DOI:10.1021/ic970737y
  11. ↑ G. Hogarth, T. Norman, Inorganica Chemica 254 167 - 171
  12. ↑ E. Robinson, S. Johnson, T. Tang, R. Gillespie, Inorg. Chem., 1997, 36, 3020
  13. ↑ G.Lewis, J. Chem. Soc., 1916, 38, 762: DOI:10.1021/ja02261a002
  14. ↑ E. Jemmis and B. Kiran, Inorg. Chem., 1998, 2110–2114 DOI:10.1021/ic970737y
Retrieved from "https://chemwiki.ch.ic.ac.uk/index.php?title=User:Xx108(module_2)&oldid=193827"