User:Xd1013
Module 3: Transition states and reactivity
The Cope rearrangement is a reaction of [3,3]-sigmatropic rearrangement of 1,5 dienes. The reaction involves the debate in the transition state, "chair" or "boat". In this computational experiment, Gaussview and Gaussian was being used to show the lowest energy transition state of Cope rearrangement. Two basis sets HF (Hartree Fock) and DFT (Density Functional Theory) were used to optimize the reaction. The methods was further applied on the frontier molecular orbital theory and show the exo- and endo- product selectivity of Diels Alder cycloaddition reaction.
Nf710 (talk) 12:54, 4 November 2015 (UTC) HF and DFT are not basis sets, withing HF and DFT you can apply all manner of different types of basis sets . HF solves the many electron wavefunction with a slater determinant, DFT uses functionals of the electron density which is less computationaly expensive as HF and can account for electron correlation etc.
What Gaussian and Gaussview did was optimizes special points on the potential energy surface (PES) and transfers the information to a visible geometry. Transition structure is the point where energy decreases in one direction along the path way (the lowest energy path). The stationary points (maximum and minimum) were first found using first derivatives at(∂E(q))/∂q=0. The secondary derivatives were used to give force constants k=(∂^2 E)/(∂q^2 ) . Frequency was obtained v=1/2π √(k/μ), where μ is the reduced mass, μ=(m1 m2)/(m1+m2 ). The transition state was at any point the optimization gives an imaginary frequency (negative k). In this experiment Gaussian would give the transition state we need and help analyse the Cope rearrangement and Diels Alder reaction.
Nf710 (talk) 12:54, 4 November 2015 (UTC) Very good understanding of how optimisations work. In guassian it is done in N dimensions (degrees of freedom) and then optimised in NxN matriix so you cant really visualise it. but good explaination!
The Cope Rearrangement
The Cope rearrangement includes a reversible transition state via "chair" or "boat" conformation.Different conformations of anti and gauche 1, 5-hexadienes were optimized under HF/3-21G.
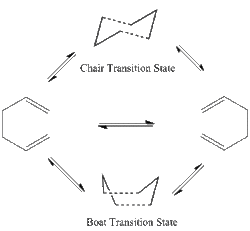
Before the experiment, the expecting lowest energy conformation was anti ones, because the anti-conformations provide less steric conflicts. But Gauche 3 conformation had the lowest energy after optimization showed in table below. The reason of this lower energy was its special structure. The C=C π orbital overlap with the adjacent C-H σ* orbital which stabilize the energy. The stabilisation occurred twice on both ends, so the energy of gauche 3 was unexpectedly lowest.
Table of structures and energies of different conformers
The 1, 5- hexadiene of anti 2 conformation was further optimized under B3LYP/6-31G* using DFT method. The structures have little difference under two methods.The Hartree Fock (HF) method includes kinetic energy of the electrons, interaction between electron and nuclei and coulomb interaction between electron clouds, while the density functional theory (DFT) includes not only HF but also exchange correlation potential due to spin and charge. Thus the structure difference shown in table below was due to the exchange correlation potential.
Nf710 (talk) 14:14, 4 November 2015 (UTC) Good knowledge of DFT and HF however, some things to point out. HF tries to solve the shrodinger equation in a single slater determinant. It treats the repulsion between electrons as a mean field for all the electrons which is one to many as it should the the potential of all the other electrons on the one electron. Therefore typically over estimates this repulsive term. DFT uses functionals of the electron density which does account of exchange correlation, but also accounts for pairing energy. But you have a good undertsanding. Very good comparison of the geometries and you were correct to not compare the energies.
Structure comparison between HF/3-21G and B3LYP/6-31G* energy level
The anti 2 conformation was further calculated the frequency to see the vibrations. The result showed that there was no imaginary frequency mod. All vibrational frequencies were positive. That is during the optimization, the molecule did not have a transition state. The thermochemistry was read from the output file, showing the potential energy at 0 k (zero-point energy), at 298.15 k and 1 atm, sum of energy includes the enthalpy and sum of energy includes free energy.
Nf710 (talk) 14:19, 4 November 2015 (UTC) The frequency calculation correctly done, with the correct understanding from the intro. thermochemistry results correct
Different energy of the Anti 2 conformer at B3LYP/6-31G* energy level
| Sum of electronic and zero-point Energies = -234.469215 |
| Sum of electronic and thermal Energies = -234.461867 |
| Sum of electronic and thermal Enthalpies = -234.460922 |
| Sum of electronic and thermal Free Energies = -234.500800 |
Optimizing the "Chair" and "Boat" Transition Structures
"Chair" Transition Structures
Two allyl fragment (CH2CHCH2) were optimized under HF/3-21G level of theory, then arranged like a "chair" conformation with terminal ends of the allyl fragments separated 2.2 Å apart. The structure was optimized and frequency calculated to TS (Berny) under HF/3-21G. The vibrational frequency showed an imaginary frequency at -817.93 cm-1. This showed there was a transition state at this point on Potential Energy Surface (PES), which illustrate bond forming and breaking in the Cope Rearrangement.
Chair imaginary vibration at transition state
The conformation was then optimized to minimum using frozen coordinate method by freezing the terminal carbons of the allyl fragments. Therefor the two pairs of end point where the bonds form and break during the transition state can be fixed and the bond length of each pair equalled to 2.2 Å.
The terminal carbons were now set derivative rather than Freeze Coordinate. The structure was optimized again after Redundant Coord. The structure and bond length were compared before and after Redundant Coord.
Structure comparison before and after Redundant Coord
From the result above, the separation between two alkyl fragments was clearly set to be 2.2 Å. The structure had also being rearranged to have a more symmetric Ci conformation. The calculation was more focused on the reaction occuring part in Redundant Coord calculation, and gave a more accurate result of the structure.
Nf710 (talk) 14:23, 4 November 2015 (UTC)Very good comparison of the geometries
"Boat" Transition Structures
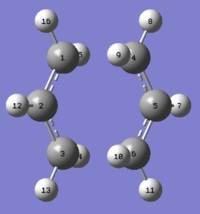
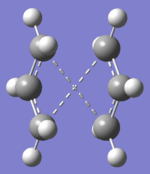
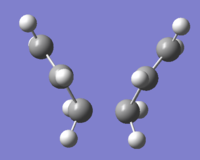
The boat transition state was optimized using the anti 2 1, 5-hexadiene. Anti 2 is a Ci symmetric molecule and simply renumber the atoms label would give both the reactant and the product of the Cope rearrangement. The reactant and product were plane symmetric so renumber the atoms as shown. When opt+ freq the reactant and product using QST2, under HF/3-21G, the output was a dissociative conformation like a “chair”. This was because the Gaussian did not consider the central C3-C4 bond rotation. After rearrange the input structures, the output now was a ‘’boat’’ conformation.
Structure of "boat" transition state
 |
|
|---|---|
 |
 |
 |
 |
Boat imaginary vibration at transition state
The vibrational frequency also gave an imaginary negative value at -839.94 cm-1, which showed the bonds form and break at transition state of [3,3]-sigmatropic rearrangement.
Nf710 (talk) 14:38, 4 November 2015 (UTC) Correctly optimised and the frequency is correct
Intrinsic Reaction Coordinate or IRC method
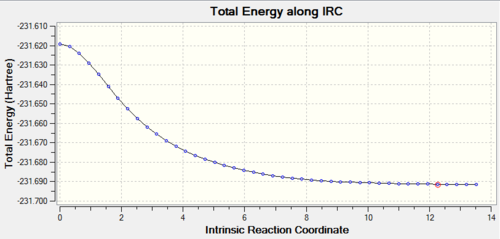
The conformation of “chair” and “boat” were both optimized. Now to find the more stable transition state, IRC method was used. IRC gave the energy level of the reaction pathway and it was the most direct way to see the lowest energy conformation. Using the optimized “chair” and “boat” chk file as inputs, under the IRC method, set 50 or more points on the IRC curve, and submit the job.
The results gave were shown in figures below. Comparing the IRC calculation results, the “chair” conformation stated at a lower energy, -231.62 Hartree and also ended up at lower energy, -231.69 Hartree. This showed that, the energy barrier to “chair” transition state was lower. Thus in the Cope rearrangement, the conformation would prefer to go to the “chair” structure which was more stable and lying at lower energy. The end of the IRC output gave a structure looked like the product, which followed the reaction coordination. The reaction went forward and formed a lower energy product after pass through the transition state.
Finally, the energy of both “chair” and “boat” were compared under two different level of theory, HF/3-21G and B3LYP/6-31G*. The structures under two calculations were roughly same, but the energy was quite different.

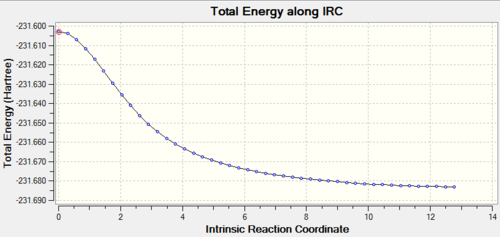
Nf710 (talk) 14:43, 4 November 2015 (UTC) IRC implimented correctly and thermochemistry looks correct. In general good knowledge of optimisations. Could have been improved with the use of JSmol and newman projections for the gauss and anti conformers. Furthermore you could looked at the MOs for the gauche 3 conf that would have shown you clearly that there are secondary orbital interactions due to the overlap of the orbitals shown in the HOMO. you also didnt compear the geometries for the higher level of theory for both TS states.
Summary of energies (in hartree)
| HF/3-21G | B3LYP/6-31G* | |||||
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | |||
| Chair TS | -231.61932233 | -231.466705 | -231.461345 | -234.55693104 | -234.414908 | -234.408980 |
| Boat TS | -231.60280200 | -231.450928 | -231.445299 | -234.54307881 | -234.402354 | -234.396011 |
| Reactant (anti2) | -231.69253528 | -231.539539 | -231.532565 | -234.61171166 | -234.469215 | -234.461867 |
Summary of activation energies (in kcal/mol)
| HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | Expt. | |
| at 0 K | at 298.15 K | at 0 K | at 298.15 K | at 0 K | |
| ΔE (Chair) | 45.70 | 44.69 | 34.08 | 33.19 | 33.5 ± 0.5 |
| ΔE (Boat) | 55.60 | 54.76 | 41.96 | 41.33 | 44.7 ± 2.0 |
Both calculations showed “chair” transition state was lower in energy and the activation energy calculated (shown in table above) was also smaller. Thus the “chair” conformation was the more stable transition state. The activation energy modelled and calculated by computational experiment was similar to the experimental one, which verify the result and illuminate the computational experiment was useful and reasonable.
The Diels Alder Cycloaddition
Ethylene and cis butadiene reaction
Diels Alder reaction is a 4+2 cycloaddition. The reaction happening or not can be judged by Woodward-Hoffmann rules. In molecular orbital, when there is a significant HOMO and LUMO orbital overlap density between two reactants, the reaction is allowed. The molecular orbitals can only interact and form bonding when the orbitals have the same symmetry.
In this experiment, the transition state of a Diels Alder Cycloaddition was found by QST2 method under HF/3-21G level of theory.The reaction began with cis butadiene and ethylene. The MO diagram showed the cis butadiene had a symmetric LUMO and an anti-symmetric HOMO. The ethylene had an anti-symmetric LUMO and a symmetric HOMO.
Table of molecular orbitals geometry and symmetry of Cis-butadiene and ethylene
| Molecule name | MO name | Orbital sketch | Orbital geometry | symmetry |
|---|---|---|---|---|
| Cis-butadiene | LUMO |  |
 |
Symmetric |
| HOMO |  |
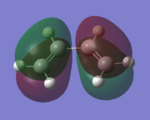 |
Anti-symmetric | |
| ethylene | LUMO | 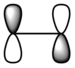 |
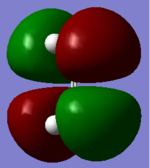 |
Anti-symmetric |
| HOMO | 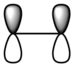 |
 |
Symmetric |
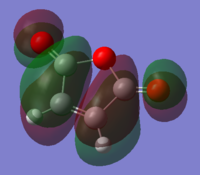
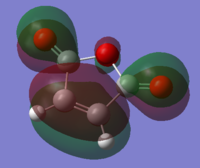
The QST2 calculation gave the transition state of the reaction and the HOMO of the structure. The MO showed the orbital combination of symmetric LUMO of cis butadiene and symmetric HOMO of ethylene. The LUMO and HOMO were both symmetric and had efficient overlap density thus the reaction was allowed.
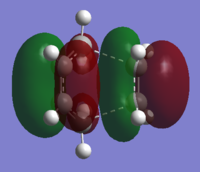
(This does not look like the HOMO of the TS. In addition, the MO of the LUMO is not present Tam10 (talk) 16:24, 27 October 2015 (UTC))
C-C Bond length in transition state of Boat conformer
| Bond | Bond length |
|---|---|
| C1-C2 | 1.37594 |
| Partially formed C2-C3 | 2.20986 |
| C3-C4 | 1.36997 |
| C4-C5 | 1.39441 |
| C5-C6 | 1.36995 |
| Partially formed C1-C5 | 2.20927 |
The bond length of the partially formed C-C bonds were 220.927 pm and 220.986 pm. While the sp3–sp3 bond length is 154 pm, sp2–sp2 is 134 pm and van der Waals radius of the C atom is 170pm[1][2]. The partially formed C-C bonds had the bond length smaller than 2 times the Van der Waals radius, showed the terminate carbons were approaching each other and start to form bonds. But the bond length also smaller than a normal C-C bond, showed the bonds were only partially formed in the transition state. Other C-C bond lengths were close to 134 pm showed electron resonance in the partially formed six member ring.

| Vibration that corresponds to the reaction path at the transition state | Lowest positive frequency of product |
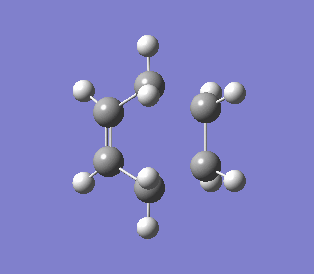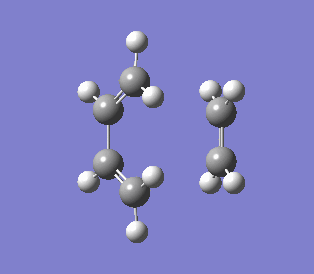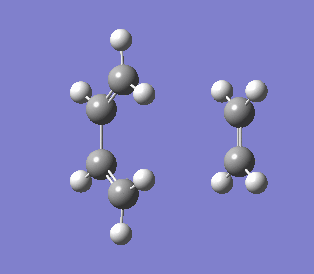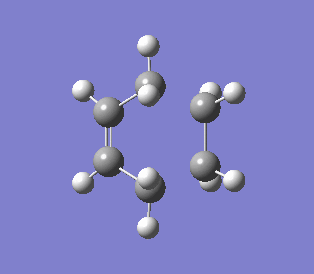 |
|
The IRC was run in both directions, so from the IRC diagram it was easy to the highest energy point while was the transition state.From the vibration showed, the formations of the two C-C bonds were synchronous. In the lowest possible energy vibration of the product (171.93 cm-1), the vibration was similar to the transition state vibration.
(What was the imaginary frequency? I don't agree with your last statement... the lowest frequency of a product tends to be independent of its formation Tam10 (talk) 16:24, 27 October 2015 (UTC))
The regioselectivity of the Diels Alder Reaction
The mechanism of the Diels Alder Reaction of cyclohexa-1,3-diene and maleic anhydride was shown. The reaction gave two regioselective products exo- and endo- adducts.
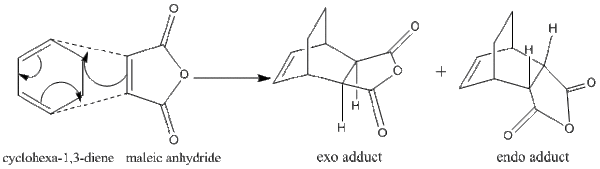
QST2 method was used by renumbering the atomic labels on the reactant and products then submit with HF/3-21G level of theory. Two transition states were obtained, exo- and endo- ones. The result of MO showed both exo- and endo- products were formed by the orbital overlap between HOMO of cyclohexa-1,3-diene and LUMO of maleic anhydride. The HOMO and LUMO overlap because they had same symmetry.
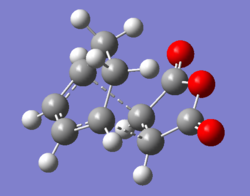
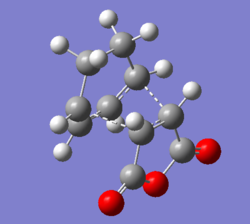
Table of molecular orbitals geometry and symmetry of reactants and products in Diels Alder reaction
| Endo- imaginary vibration | Exo- imaginary vibration |
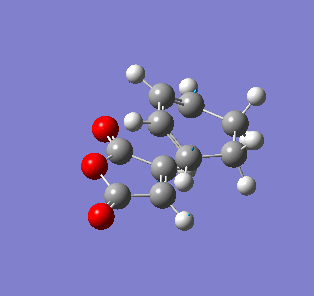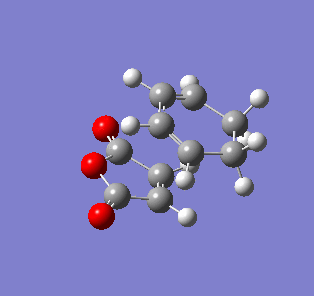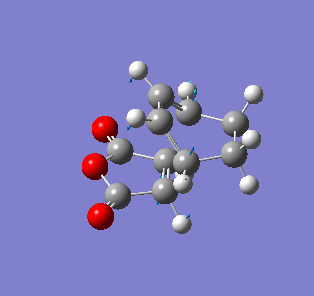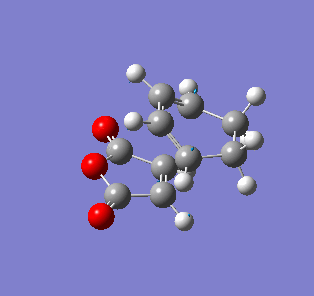 |
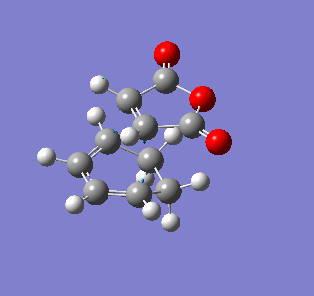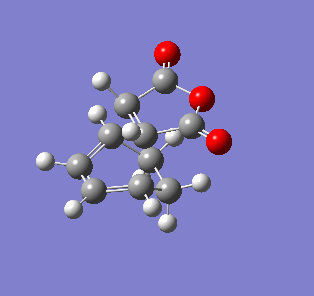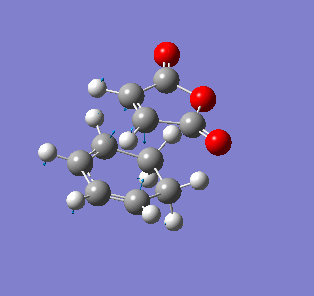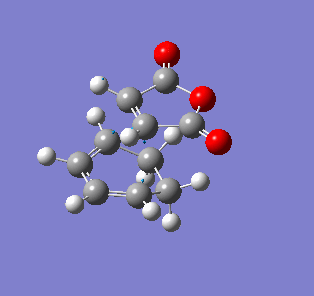
|
The endo transition state had an imaginary vibration frequency at -643.90 cm-1 ,while the exo- one had it at -647.46 cm-1. From the HOMO of the products, the exo-adduct showed only primary interaction between the diene and the maleic anhydride. The carbon adjacent to oxygen did not contribute its orbital to the HOMO in the product. The endo product had more overlap density. There were two pairs of π bond orbital overlap shown in figure below. Therefor the endo product was favoured. The computational output showed the energy of then endo product was -605.6104 Hartree, while then energy of the exo product was -605.6036 Hartree.With the same starting martial, the reactant energies were same, thus the activation energy for exo-adduct was higher than the endo-adduct, which also showed the endo adduct was the favoured kinetic product.
(Convert your energies to KJ/mol or Kcal/mol. You're confusing activation energy and reaction enthalpy, transition structures and products. Can you elaborate on why you think the activation energies and reaction enthalpies are different? Tam10 (talk) 16:24, 27 October 2015 (UTC))
Further discussion
All the calculation in this part were HF/3-21G, thus the calculation was approximated and not include spin and charge interaction. The experiment was done by computation so real situation problems such as solvent effect were not include.
References
- ↑ Fox, Marye Anne; Whitesell, James K. (1995). Organische Chemie: Grundlagen, Mechanismen, Bioorganische Anwendungen. Springer.ISBN 978-3-86025-249-9.
- ↑ Huheey, pps. A-21 to A-34; T.L. Cottrell, "The Strengths of Chemical Bonds," 2nd ed., Butterworths, London, 1958; B. deB. Darwent, "National Standard Reference Data Series," National Bureau of Standards, No. 31, Washington, DC, 1970; S.W. Benson, J. Chem. Educ., 42, 502 (1965).
- ↑ Mmurali13, 22 April 2009, https://commons.wikimedia.org/wiki/File:Cyclopentadiene_Maleic_Anhydride_Diels_Alder.png