User:Wf710

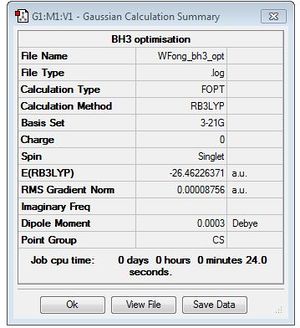
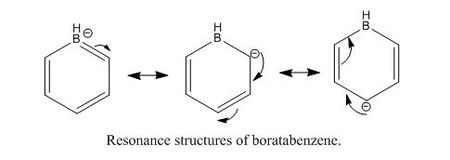
BH₃

B3LYP/3-21G level

Optimisation log file here

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000217 0.000450 YES RMS Force 0.000105 0.000300 YES Maximum Displacement 0.000692 0.001800 YES RMS Displacement 0.000441 0.001200 YES	optimised BH3 molecule

B3LYP/6-31G(d,p) level

Optimisation log file here

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000203 0.000450 YES RMS Force 0.000098 0.000300 YES Maximum Displacement 0.000867 0.001800 YES RMS Displacement 0.000415 0.001200 YES	optimised BH3 molecule

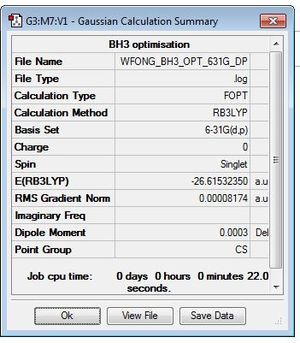
GaBr₃

B3LYP/LANL2DZ

optimisation file: DOI:10042/195211

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000000 0.000450 YES RMS Force 0.000000 0.000300 YES Maximum Displacement 0.000003 0.001800 YES RMS Displacement 0.000002 0.001200 YES Predicted change in Energy=-1.307736D-12 Optimization completed. -- Stationary point found.	optimised GaBr3 molecule

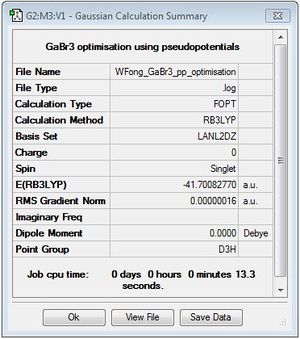
BBr₃

B3LYP/6-31G(d,p)LANL2DZ (GEN, using a mixture of basis-sets and psuedo-potentials)

optimisation file: DOI:10042/195214

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000019 0.000450 YES RMS Force 0.000012 0.000300 YES Maximum Displacement 0.000114 0.001800 YES RMS Displacement 0.000068 0.001200 YES Predicted change in Energy=-1.648522D-09 Optimization completed. -- Stationary point found.	optimised BBr3 molecule

EX₃ Discussion

Geometry Data

	BH3	BBr3	GaBr3
r(E-X)	1.19	1.93	2.35
θ(X-E-X)	120.0	120.0	120.0

Discussion of bond lengths and angles

Changing the ligand and the central element did not affect the trigonal planar bond angle of 120.0° (accurate to 1 d.p); this is expected for all three of these molecules (D_3h point group).

Calculations have showed that changing the ligand (BH₃ v.s. BBr₃) would, however, have an effect on the E-X bond length. Both the B-H and B-Br bonds are single bonds, as both H and Br have a valency of 1. However, the B-H bond is shorter than the B-Br bond. This is due to more efficient overlap of the B and H(1s) atomic orbitals (AOs), due to greater size matching of the small B and H (120 pm) atoms. In contrast, a size mismatch is notable in the B-Br bond, due to the relatively larger Br (195 pm) atom. As orbital overlap is poorer and less efficient, the B-Br bond is longer and weaker. In addition to relative size considerations, the differing electronegativities of the H and Br atoms would possibly have an effect on the variable bond length. There is a smaller difference in electronegativity value between B (2.04) and H (2.20), in contrast to that between B (2.04) and the electronegative Br (2.96) atom. While we might expect that the B-Br bond would have greater ionic character (and hence, greater strength) than the B-H bond, this is likely to be insignificant, as it does not agree with calculated values. Instead, a more likely argument would be that a small difference in electronegativity values would result in better energy matching of the corresponding AOs, and this would explain the greater stabilisation of the bonding orbitals in BH₃, in contrast to BBr₃. This is because orbitals interact more strongly if there is a small energy difference between the orbitals. As electronegativity affects the energies of the AOs, such a line of argument would rationalise the shorter B-H bonds (v.s. B-Br).

However, this analysis assumes a purely covalent bonding approach; ionic contributions could possibly also influence the bond length. In BH3, the calculated bond length values match up to literature values (DOI:10.1063/1.461942 ), suggesting covalent B-H bonds (unsurprising due to small difference in electronegativity between the atoms). However, in BBr3, the calculated bond length value is significantly smaller than reported in literature (DOI:10.1039/B801115J ). This can be attributed to BBr3's Lewis acidity - there is a possible pi-interaction between the filled 3p-orbitals of Br, and the vacant 2p-orbitals of the B atoms. Such stabilising pi-interactions would shorten and strengthen the B-Br bond.

Changing the central element (BBr₃ v.s. GaBr₃) would also affect the E-X bond length, even though both B and Ga are in Group 13. Calculations show that the Ga-Br bond is longer and weaker than the B-Br bond. This can, once again, be rationalised by the ideas of size and energy matching invoked above. As Ga (period 4) is larger than B, the Ga AOs are more diffuse than the B AOs. This results in poorer, less efficient orbital overlap with the Br AOs, resulting in weaker Ga-Br bonds. In addition, with a greater electronegativity difference between Ga (1.81) and Br (2.96) in contrast to that between B (2.04) and Br (2.96), there is a greater energy mismatch between the Ga and Br AOs, due to the larger energy gap between their AOs (electronegative elements have lowered AO energies, while electropositive elements have higher AO energies). This explains the longer and weaker Ga-Br bond, in contrast to the B-Br bonds. In addition, as the Ga orbitals are much more diffuse than the B orbitals, the stabilising pi-type interactions (described in BBr3) is less significant here; explaining GaBr3's bond length which matches well with literature (DOI:10.1016/S0022-2860(97)00420-1 ).

What is a bond?

A chemical "bond" or "bonding orbital" can be viewed as a region of electron density, which results from constructively-interfering atomic orbitals. Conversely, an antibonding orbital interaction would arise from destructive interference of the AOs. Electrons which populate the bonding molecular orbitals in a molecule have a higher probability of being located in the internuclear region, which arises from orbital overlap. In contrast to a non-bonding orbital, a bonding orbital would be lower in energy, while an antibonding interaction would raise the energy of the antibonding orbital. Bonding interactions involve the formation of molecular orbitals which are lowered in energy, in comparison to the initial atomic orbitals. The magnitude of such a stabilisation energy would depend on the extent of orbital overlap, orbital coupling, and the energy difference between the atomic or fragment orbitals. This supports the size and energy arguments proffered above in this section - orbital overlap is stronger for similarly-sized atoms, with small orbitals preferred to large, diffuse orbitals. In addition, a smaller energy gap between the orbitals would result in a greater energy stabilisation. Orbitals which are degenerate will result in a large stabilisation of the bonding orbitals, and a larger destabilisation of the anti-bonding orbitals.

An example of a 'strong' bond is that as found in a N₂ molecule. Being a triple bond (942 kJ/mol), it is formally considered as a sigma bond, in addition to two pi-bonding interactions using the 2 unhybridised and orthogonal N(2p)-orbitals. Good orbital overlap is seen, due to the strong interaction between the small N orbitals which are well-matched in size. A large HOMO-LUMO gap exists for such a strong bond, and this is accentuated by the degenerate N atoms, which would contribute to this large stabilisation energy (due to a large energy splitting). Another example of a 'strong' bond is the strong ionic bond between oppositely-charged ions with high charge densities (and low polarisabilities for the anion); for example, the ionic bonding exhibited between Al³⁺ and O^2- ions. A bond of 'medium' strength could possibly be a C-C single bond (≈350 kJ/mol). Weak bonding interactions can be non-covalent in nature, such as the weak van der Waal's intermolecular forces of attraction between molecules, or the weak π-π stacking between aromatic rings (<10 kJ/mol). These are bonding interactions which require much smaller amounts of energy to overcome.

In some compounds, GaussView does not show a bond is present; the program uses a set of pre-defined distance-based criteria to assess if a bond is present. The program will not show a bond, if the atomic separation is larger than this pre-defined expected value. The definition of "bonds" in GaussView is a structural convenience, and is not always foolproof. In particular, while the determination of bonds in typical organic compounds might be easy, GaussView might not be able to detect bonds as effectively in inorganic compounds, where long atomic separations might actually have a bonding interaction which is not detectable by GaussView. It would be preferable to consult literature values (e.g. van der Waals radii of individual atoms), in conjunction with analytical techniques like X-ray crystallography or IR spectroscopy (determination of force constants) etc. to assess the presence of a "bonds", instead of relying on GaussView's pre-existing database. This is accentuated by the idea that while bonds in organic molecules are often well-defined (e.g. distinguishing between single and triple C-C bonds), in contrast to inorganic compounds or complexes.

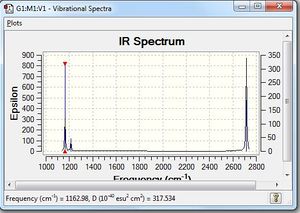
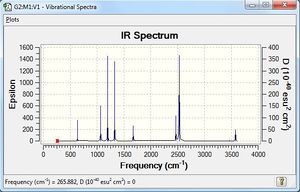
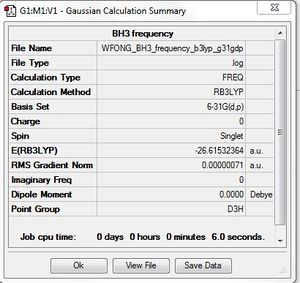
BH₃:B3LYP/6-31G(d,p): Frequency Analysis

Frequency file: here

summary data	low modes
	Low frequencies --- -10.1940 -10.1821 -3.1776 -0.0008 0.0579 0.4920 Low frequencies --- 1162.9850 1213.1461 1213.1463

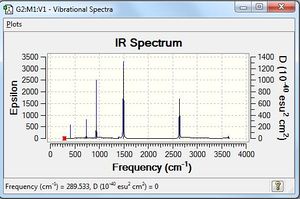
Vibrational spectrum for BH₃

wavenumber	Intensity	IR active?	type
1163	93	yes	bend
1213	14	very slight	bend
1213	14	very slight	bend
2583	0	no	stretch
2716	126	yes	stretch
2716	126	yes	stretch

|

While 6 vibrations are observed in the animation, the simulated IR spectrum only shows 3 vibrational peaks. The bond stretching at 2583 cm^-1 does not result in any change in the dipole moment; hence, it is not IR-active. In addition, two sets of degenerate vibrations are seen - the bending motion at 1213 cm^-1 has two degenerate bends, while the 2716 cm^-1 peak involves two degenerate IR-active stretches. As there are two degenerate modes of E' symmetry, this reduces 4 potential bands to 2. There are hence 3 vibrational peaks observed in the simulated IR spectrum. However, the peak at 1213 cm^-1 is of a very low intensity, and it is probable that this is not observable in an actual IR spectrum.

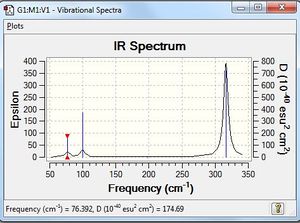
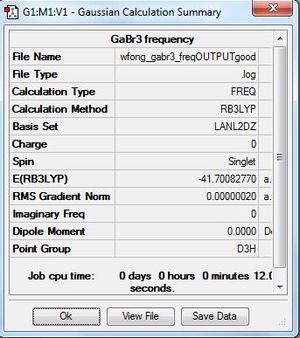
GaBr₃ Frequency Analysis

Frequency file: DOI:10042/195233

summary data	low modes
	Low frequencies --- -1.4878 -0.0015 -0.0002 0.0096 0.6540 0.6540 Low frequencies --- 76.3920 76.3924 99.6767

Vibrational spectrum for GaBr₃

wavenumber	Intensity	IR active?	type
76	3	very slight	bend
76	3	very slight	bend
100	9	very slight	bend
197	0	no	stretch
316	57	yes	stretch
316	57	yes	stretch

|

GaBr3, just like BH3, shows 3 vibrational peaks, although there are a total of 6 vibrations. The vibration at 197 cm-1 was not IR active; the three Ga-Br bonds are symmetrically stretched in the trigonal planar GaBr3 molecule, and this results in no change in the dipole moment (hence it is not IR-active). The two bending motions at 76 cm-1 are degenerate, and the two stretching motions at 316 cm-1 are also degenerate. This hence results in a total of 3 peaks.

What does the large difference in the value of the frequencies for BH3 compared to GaBr3 indicate?

The range for GaBr3's vibrations (76 cm-1 to 316 cm-1) are much lower than that of BH3 (1163 cm-1 to 2716 cm-1). This can be attributed to the greater reduced mass of the Ga-Br bond, in contrast to the B-H bond (lower reduced mass). A greater reduced mass results in a lower stretching frequency in GaBr3 (cf BH3). The frequencies observed are inversely proportional to the square root of the reduced mass, hence explaining the higher wavenumbers of the IR absorptions in BH3. In addition, the B-H bond force constant (the square root of which is proportional to the wavenumber of IR absorption) is higher than the Ga-Br force constant, owing to better atomic orbital overlap, mainly due to size matching considerations.

Reordering of umbrella mode

Of particular interest was the A2 umbrella motion which was observed in both BH3 and GaBr3. This occurred at 1163 cm-1 (intensity 93) in BH3; however, a reordering of modes was seen in GaBr3 (100 cm-1, intensity 9), where a similar vibration was of a higher frequency than the degenerate E' bending modes.

For the A2 umbrella motion, only a displacement (from the equilibrium position) in the z-coordinate is observed; hence indicating the umbrella mode.

In BH3, a greater displacement was seen for the H atom (displacement -0.57) in contrast to the B atom (displacement 0.16). This analysis was next conducted on GaBr3, to evaluate if it was typical for the central atom (B in BH3, Ga in GaBr3) to be displaced less than the 'ligand' (i.e. H in BH3, Br in GaBr3).

However, in contrast to BH3, the Ga central atom (displacement 0.89) was displaced more than the 'ligand' Br atom (displacement -0.26).

This suggests that it is the atom of lower atomic mass which would undergo a larger displacement. In BH3, the lighter H atom would be displaced (in the z-coordinate) to a larger extent than the B atom. Similarly, in GaBr3, the lighter Ga atom is displaced less than the heavier Br atom, during the A2 umbrella mode.

Why must you use the same method and basis set for both the optimisation and frequency analysis calculations? What is the purpose of carrying out a frequency analysis? What do the "Low frequencies" represent?

During the optimisation of a structure, an ideal stable point is obtained, via repetitively solving the Schrodinger equation. This will result in the optimal nuclear positions, in tandem with its concomitant electronic arrangement, which would represent the lowest energy structure (minima on potential energy surface). The changing coordinates of the nuclei and electrons result in a series of different energies, along the potential energy surface. Using a higher basis set involves using a larger number of functions, which are used to describe the electronic structure. The same method should be used (in order to draw comparisons); this ensures that the operator for the Schrodinger equation is the same, and the same basis set is used to ensure that the wavefunctions used in the calculations are identical. The use of a higher basis set would potentially result in a slight, but non-negligible, change in the molecule's structure (i.e. bond length, bond angle etc.) Hence, a fair comparison can only be conducted if the same method/basis set is used for the optimisation and frequency analysis for different molecules. Otherwise, features of the optimised structure (e.g. energy) cannot be compared between two 'optimised' molecules which are derived from different optimisation methods/basis sets.

Upon successful optimisation, a frequency analysis is necessary, to confirm successful discovery of the minium structure. The frequency analysis is related to the 2nd derivative of the potential energy (P.E.) surface. If one negative frequency is observed, this represents the presence of a transition state (energy maxima). However, if more than one negative frequency is observed, a critical point has not been found (or the optimisation is unsuccessful/incomplete etc).

A non-linear molecule has 3N-6 vibrational frequencies. The "low frequencies" section present in each section of the frequency analysis for different molecules represents the 6 low frequencies which consist of the "-6" (in 3N-6). These 6 low frequencies represent the movement of the molecule's centre of mass (the translational and rotational frequencies). It is ideal that the "low frequencies" section involve values which are as close to 0 as possible; this suggests successful/ideal methods and structural optimisation (the lower the better!).

Molecular Orbitals of BH₃

Completed Population Analysis file: DOI:10042/195249

An annotated MO diagram of BH₃, with "real" and "LCAO" MOs.

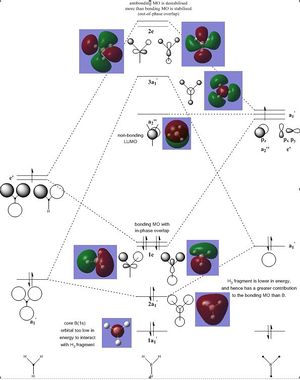
The LCAO MOs show good agreement with the real MOs as depicted in the thumbnail above. Qualitative MO theory, which utilises LCAO in predicting the shapes and energies of these ensuing MOs, is hence quite accurate, as shown in the example of BH₃. Qualitative MO theory is also useful in aiding our understanding of the bonding and chemistry in the compound; for instance, the MO diagram suggests a low-lying non-bonding LUMO which explains the Lewis acidic nature of the electron-deficient BH₃ centre. However, relying on qualitative MO theory can sometimes lead to difficulties in predicting the relative energies of different MOs; this is especially challenging in the case of MOs which are close in energy, or when there is mixing of the MOs. A calculation of the actual MOs and their energies is hence useful, in giving us a better idea of the relative energies of these MOs. A good understanding of the relative energies of these MOs would also aid our understanding and analysis of the chemistry of the molecule in question. Nevertheless, for relatively small and simple molecules such as BH₃, qualitative MO theory acts as a very useful and convenient "starting point" in predicting the chemistry and bonding/anti-bonding nature of the corresponding MOs. Calculations will then help to confirm or improve the understanding which was initially derived using qualitative MO theory.

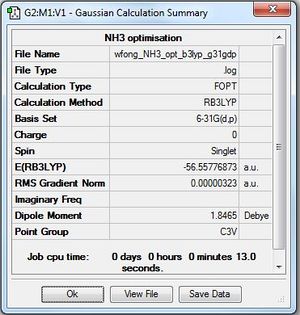
NH₃

Optimisation: B3LYP/6-31G(d,p)

Optimisation log file here

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000006 0.000450 YES RMS Force 0.000004 0.000300 YES Maximum Displacement 0.000012 0.001800 YES RMS Displacement 0.000008 0.001200 YES Predicted change in Energy=-9.844530D-11 Optimization completed. -- Stationary point found.	optimised NH3 molecule

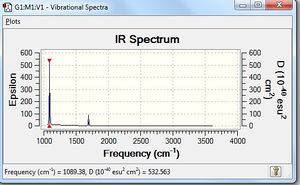
Frequency Analysis

Frequency file: here

summary data	low modes
	Low frequencies --- -0.0129 -0.0027 0.0005 7.0724 8.1020 8.1023 Low frequencies --- 1089.3849 1693.9369 1693.9369

Vibrational spectrum for NH₃

wavenumber	Intensity	IR active?	type
1089	145	yes	bend
1694	14	very slight	bend
1694	14	very slight	bend
3461	1	no	stretch
3590	0	no	stretch
3590	0	no	stretch

|

Molecular Orbitals of NH₃

Completed Population Analysis file: DOI:10042/195250

NBO Analysis of NH₃

By utilising a colour range of -1 (red) to +1 (green), an image of the charge distribution of NH₃ is generated:

|

As is expected, the electronegative N atom is bright red (highly negatively charged), while the H atoms are bright green.

By selecting the "show numbers" option, the specific NBO charges for the N and H atoms were found to be -1.125 and +0.375, respectively.

BH₃NH₃

Optimisation: B3LYP/6-31G(d,p)

Optimisation log file here

summary data	convergence	Jmol
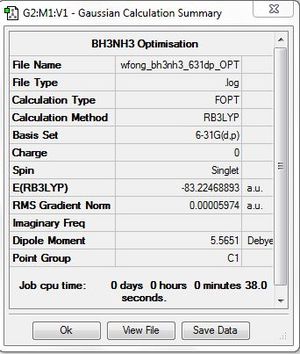
	Item Value Threshold Converged? Maximum Force 0.000123 0.000450 YES RMS Force 0.000058 0.000300 YES Maximum Displacement 0.000515 0.001800 YES RMS Displacement 0.000296 0.001200 YES Predicted change in Energy=-1.635696D-07 Optimization completed. -- Stationary point found.	optimised BH3NH3 molecule

Frequency Analysis

Frequency file: here

summary data	low modes
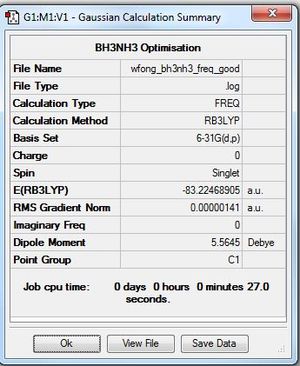
	Low frequencies --- -6.6928 -0.0012 -0.0004 0.0010 0.3164 2.5837 Low frequencies --- 263.3236 632.9510 638.4259

wavenumber	intensity	IR active	type
263	0	no	bend
633	14	slight	stretch
638	4	no	bend
638	4	no	bend
1069	41	yes	bend
1069	41	yes	bend
1196	109	yes	bend
1204	3	no	bend
1204	3	no	bend
1329	114	yes	bend
1676	28	yes	bend
1676	28	yes	bend
2470	67	yes	stretch
2530	231	yes	stretch
2530	231	yes	stretch
3463	3	no	stretch
3580	28	yes	stretch
3580	28	yes	stretch

|

Determination of Association Energy

The relative energies of the following compounds can be computed, as the following energy values were calculated using identical methods and basis sets (as detailed above).

E(NH₃) = -56.5577687 a.u.

E(BH₃) = -26.6153235 a.u.

E(NH₃BH₃) = -83.2246889 a.u.

ΔE = E(NH₃BH₃) - [E(NH₃)+ E(BH₃)] = -0.0515967 a.u. = -135.0 kJ/mol (Error range of 10 kJ/mol)

With reference to the earlier discussion, the association energy in B-N bond formation is in the same order of magnitude as a medium strength bond (e.g. C-C). Based on this analysis, the association of NH₃ and BH₃ (i.e. B-N bond formation in the adduct) involves the formation of a medium strength bond.

Benzene

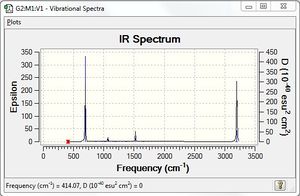
Optimisation: B3LYP/6-31G(d,p)

Optimisation log file here

summary data	convergence	Jmol
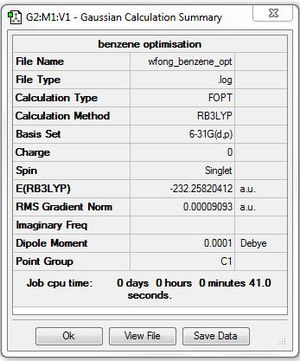
	Item Value Threshold Converged? Maximum Force 0.000198 0.000450 YES RMS Force 0.000082 0.000300 YES Maximum Displacement 0.000849 0.001800 YES RMS Displacement 0.000305 0.001200 YES Predicted change in Energy=-4.741875D-07 Optimization completed. -- Stationary point found.	optimised benzene molecule

Frequency Analysis

Frequency file: here

summary data	low modes
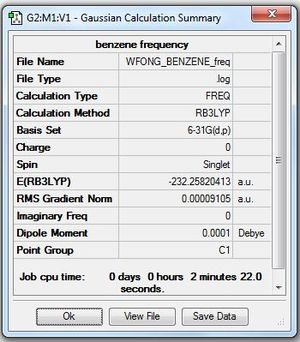
	Low frequencies --- -13.7810 -12.9763 -11.9029 -0.0010 -0.0004 -0.0002 Low frequencies --- 414.0699 414.1914 620.9703

wavenumber	intensity	IR active	type
414	0	no	bend
414	0	no	bend
621	0	no	bend
621	0	no	bend
693	74	yes	bend
718	0	no	bend
864	0	no	bend
864	0	no	bend
974	0	no	bend
974	0	no	bend
1012	0	no	bend
1018	0	no	bend
1020	0	no	ring breathing
1066	3	no	bend
1066	3	no	bend
1179	0	no	bend
1202	0	no	bend
1202	0	no	bend
1356	0	no	stretch
1380	0	no	bend
1524	7	no	bend
1524	7	no	bend
1653	0	no	stretch
1653	0	no	stretch
3174	0	no	stretch
3184	0	no	stretch
3184	0	no	stretch
3200	47	yes	stretch
3200	47	yes	stretch
3210	0	no	stretch

|

Molecular Orbitals of Benzene

Completed Population Analysis file: DOI:10042/195300

NBO Analysis of Benzene

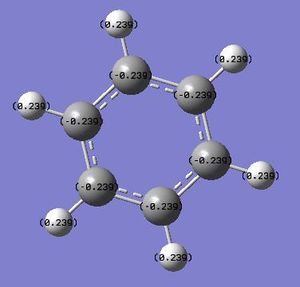
By utilising a colour range of -1 (red) to +1 (green), an image of the charge distribution of benzene is generated:

By selecting the "show numbers" option, the specific NBO charges for the C and H atoms were found to be -0.239 and +0.239, respectively.

MO Analysis of Benzene

Aromaticity is commonly known to involve 4n+2 pi electrons delocalised via resonance in a conjugated system, involving pi-overlap of contiguous p-orbitals in a ring. Benzene is commonly mentioned as an example of an aromatic compound, with 6 pi-electrons in this conjugated system involving a planar ring; each of the C(2p) orbitals contributes 1 pi-electron each. The resulting pi-electron density (which contributes to such aromaticity) lies above and below the ring (i.e. the sigma framework); the 2p-orbitals in this planar ring arrangement have nodes lying in the ring plane of the sigma framework. Benzene's isoelectronic analogues (boratabenzene, pyridinium and borazine) are also aromatic. In our initial exploration of aromaticity as a chemical concept, an orbital diagram which would rationalise aromaticity is commonly depicted as follows:

Such a depiction is typically utilised to rationalise aromaticity; however, this treatment does not stand up to sufficient scrutiny. De-constructing the MOs reveal that the orbital diagram above involves a MO of a_2u symmetry. This occupied, fully pi-bonding MO contains 2 electrons. It would hence be insufficient to attribute benzene's aromaticity to this particular MO, as 6 pi-electrons are involved in benzene's aromatic nature. This particular a_2u MO is definitely a contributor to benzene's aromaticity, but it is not the sole contributor.

It is imperative to identify other MOs which do also play a part in making benzene aromatic. These MOs should have pi-symmetry, as the 6 electrons which are involved in aromaticity must be pi-electrons, by definition. The degenerate MOs which are also the HOMO of benzene (e_1g symmetry) would be expected to contribute the other 4 pi-electrons which are needed to rationalise benzene's aromaticity. These two degenerate MOs have pi-symmetry with two nodal planes, with a set of 3 adjacent C 2p-orbitals with fully pi-bonding interactions, and 3 other adjacent 2p-orbitals with fully pi-bonding interactions (but these 3 orbitals are out-of-phase with the other 3 orbitals!). A combined consideration and analysis of these 3 MOs are required to grasp the observed aromaticity of benzene, with 6 pi-electrons contributing to the electron density observed above and below the ring-plane of benzene's sigma framework.

In conclusion, aromaticity hence involves the delocalisation of pi-electron density [4n+2 pi-electrons (n=1 for benzene)], and this MO analysis has suggested that our common depiction of fully in-phase 2p-orbitals is insufficient in describing aromaticity (it is just a MO which contains 2 electrons). The other 4 electrons should arise from the 2 degenerate e_1g MOs with pi-symmetry. Aromaticity is hence a concept which goes beyond the over-simplistic depiction of fully in-phase pi-bonding p-orbitals; other MOs with pi-bonding character might have to be invoked and included, in order to rationalise aromaticity.

It is also worth noting that the stability of benzene is also related to the formation of strong sigma bonds within the planar sigma framework; with a strain-free six-membered ring being formed. The combination of sigma and pi- symmetry MOs contribute jointly to the observed stability of these aromatic compounds.

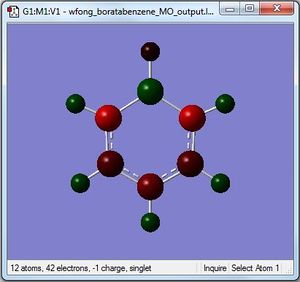
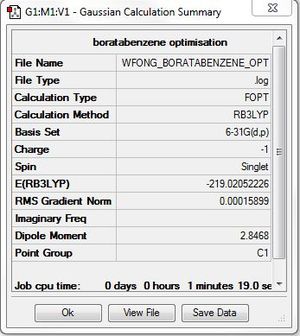
Boratabenzene

Optimisation: B3LYP/6-31G(d,p)

Optimisation log file here

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000160 0.000450 YES RMS Force 0.000069 0.000300 YES Maximum Displacement 0.000887 0.001800 YES RMS Displacement 0.000328 0.001200 YES Predicted change in Energy=-6.637848D-07 Optimization completed. -- Stationary point found.	optimised boratabenzene molecule

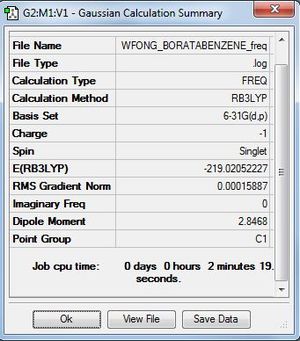
Frequency Analysis

Frequency file: here

summary data	low modes
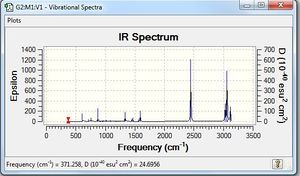
	Low frequencies --- -6.6196 -0.0010 -0.0009 -0.0003 4.1775 5.5778 Low frequencies --- 371.2576 404.5247 565.1726

|

Molecular Orbitals of Boratabenzene

Completed Population Analysis file: DOI:10042/195306

NBO Analysis of Boratabenzene

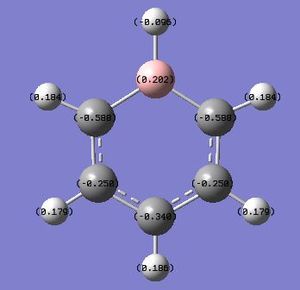
By utilising a colour range of -1 (red) to +1 (green), an image of the charge distribution of boratabenzene is generated. Evidently, the electropositivity of B is evident; the B atom shows up as bright green.

By selecting the "show numbers" option, the specific NBO charges for the B, C and H atoms were as follows:

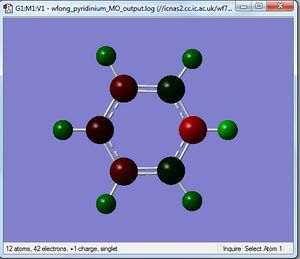
Pyridinium

Optimisation: B3LYP/6-31G(d,p)

Optimisation log file here

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000065 0.000450 YES RMS Force 0.000023 0.000300 YES Maximum Displacement 0.000837 0.001800 YES RMS Displacement 0.000178 0.001200 YES Predicted change in Energy=-7.098569D-08 Optimization completed. -- Stationary point found.	optimised pyridinium molecule

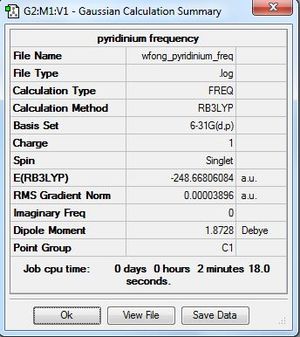
Frequency Analysis

Frequency file: here

summary data	low modes
	Low frequencies --- -9.4967 -5.6228 -0.0007 0.0005 0.0005 4.4766 Low frequencies --- 391.8976 404.3544 620.1951

|

Molecular Orbitals of Pyridinium

Completed Population Analysis file: DOI:10042/195307

NBO Analysis of Pyridinium

By utilising a colour range of -1 (red) to +1 (green), an image of the charge distribution of pyridinium is generated. Evidently, the electronegativity of N is evident; the N atom shows up as bright red.

By selecting the "show numbers" option, the specific NBO charges for the N, C and H atoms were as follows:

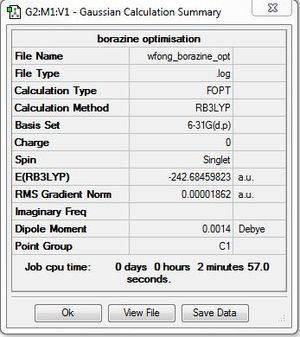
Borazine

Optimisation: B3LYP/6-31G(d,p)

Optimisation log file here

summary data	convergence	Jmol
	Item Value Threshold Converged? Maximum Force 0.000023 0.000450 YES RMS Force 0.000009 0.000300 YES Maximum Displacement 0.000434 0.001800 YES RMS Displacement 0.000152 0.001200 YES Predicted change in Energy=-2.264806D-08 Optimization completed. -- Stationary point found.	optimised borazine molecule

Frequency Analysis

Frequency file: here

summary data	low modes
	Low frequencies --- -8.9191 -5.9449 -0.0006 0.0006 0.0007 3.6494 Low frequencies --- 289.5328 289.6019 404.3988

|

Molecular Orbitals of Borazine

Completed Population Analysis file: DOI:10042/195308

NBO Analysis of Borazine

By utilising a colour range of -1 (red) to +1 (green), an image of the charge distribution of borazine is generated:

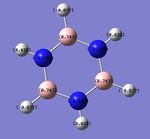
By selecting the "show numbers" option, the specific NBO charges for the B, N and H atoms were as follows:

Comparison of Charge Distribution

Comparison of Charge Distributions of Aromatic Compounds

	Benzene	Boratabenzene	Pyridinium	Borazine
Charge Distribution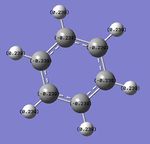
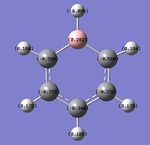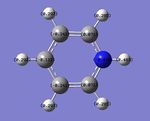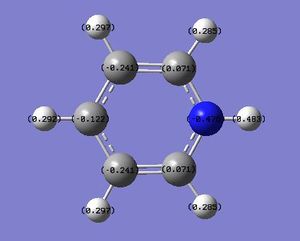
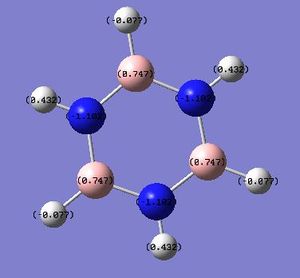
Specific NBO Charges	C: -0.239 H: +0.239	B: +0.202 C: -0.588, -0.250, -0.340 H: -0.095 (BH), +0.588, +0.179, +0.186	N: -0.470 C: +0.071, -0.241, -0.122 H: +0.483 (NH), +0.285, +0.297, +0.292	B: +0.747 N: -1.102 BH: -0.077 NH: +0.432

The charge distribution for benzene is easily rationalised, as the C atom is more electronegative than the H atom. The C-H bonds all would be expected to have the electron density in the bonding orbitals polarised towards the C atom. In addition, owing to the symmetry of the benzene molecule, all of the C and H atoms in the ring are equivalent (with identical calculated charge densities).

Boratabenzene involves the substitution of a "C-H" unit with a "B-H" unit, and this involves adding a negative charge to the molecule. With a reduction of symmetry observed (D6h to C2v), the C atoms are no longer calculated to have equal charge densities. The 2 C atoms directly adjacent to the electropositive B atom have the most negative charge densities, owing to the greater polarisation of the C-B bond, due to a greater difference in electronegativities. Similarly, the H atom bonded to B is negatively-charged (charge of -0.095), as the B atom is less electronegative than the H atom. It is interesting to note that among the 3 C atoms which are yet to be discussed, the 1 C atom which is para- to the B atom is the more negatively charged (-0.340), in contrast to the 2 C atoms which have a lower negative charge (-0.250). A simple consideration of inductive effects (i.e. proximity to the electropositive B atom) is hence insufficient; instead, drawing the resonance forms of the boratabenzene anion would show that the negative charge can lie on the C-2 and C-4 atoms, but not the C-3 atoms! The resonance diagram is as follows:

This is an interesting point, as the negative charge can sometimes be mistakenly thought to reside on the B atom, which is inaccurate - the negative charge is delocalised around the ring, and the B atom has a positive charge density (+0.202).

A similar analysis can be applied to pyridinium - the N atom is negatively charged (-0.470) due to its greater electronegativity, while the C-2 carbon is positively charged (+0.071) due to its lower electronegativity. Resonance forms can be drawn, as follows, to support the data showing that the C-4 atom is more positively charged than the C-3 atom; the resonance forms show positive charges on the C-2 and C-4, but not the C-3 atom. In addition, the H atom which is directly bonded to the N atom is the most positively-charged, as it is adjacent to the electronegative N atom.

In borazine, the B atoms are positively-charged (+0.747) as expected, as they are bonded to the electronegative N atom (-1.102), with strong polarisation of the B-N bond. Similarly, the H atoms in the B-H bonds are negatively charged (-0.077) due to their greater electronegativity than B, while the H atoms in the N-H bonds are positively charged (+0.432) for the reverse reason. This suggests that significant ionic character in borazine's bonding could reduce the aromaticity-derived energetic stability of borazine. This suggests that unlike benzene, the charges in borazine are more localised (resonance delocalisation is less extensive in borazine, in contrast to benzene). The polarisation of the B-N bond is arguably a crucial factor which influences its reactivity - borazine is involved in electrophilic addition reactions, instead of merely participating in substitution reactions (as benzene does). This increased reactivity can be rationalised by invoking the strong polarisation of the B-N bond, which results in addition reactions occurring, at the expense of the energetic cost involved in the loss of aromaticity in the molecule. This suggests that the energetic stabilisation arising from aromaticity is smaller in borazine, in contrast to benzene. The NBO analysis has shown the polar B-N bonds which can be attacked by electrophiles; the regioselectivity of these addition reactions are high (also due to the polarity of these B-N bonds). NBO analysis is hence useful in understanding the surprising reactivity, and regioselectivity, of the aromatic borazine molecule.

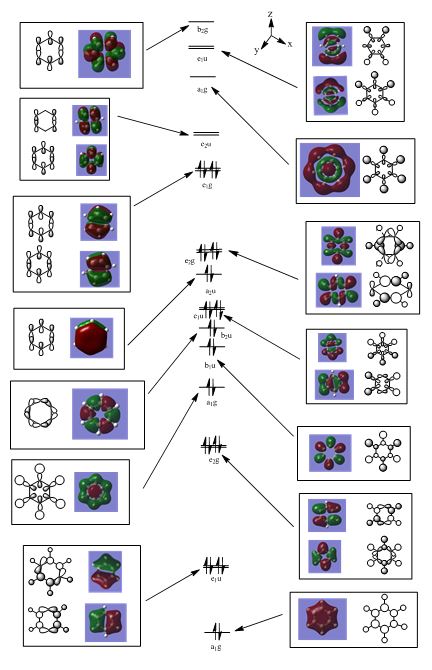
Comparison of Molecular Orbitals

Comparison of Molecular Orbitals of Aromatic Compounds

	Benzene	Boratabenzene	Pyridinium	Borazine
MO 13
Energy (au)	-0.45822	-0.20944	-0.69952	-0.38645
MO 21
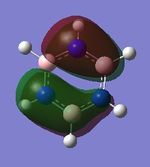
Energy (au)	-0.24691	0.01093	-0.50846	-0.27593
MO 16
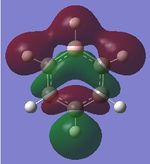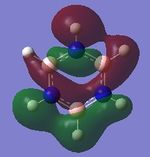
Energy (au)	-0.41656	-0.16871	-0.66589	-0.43403

The MOs of boratabenzene are generally higher in energy than benzene, while pyridinium's MOs were lower in energy. This can be due to the electronegativity of the N atom lowering the pyridinium MO energy levels, while the electropositive B atom in boratabenzene results in higher energy MOs. Meanwhile, the energies of borazine's MOs were generally similar to benzene, suggesting that the effects of the electropositive B and electronegative N atoms cancel out.

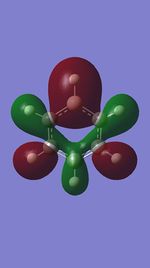
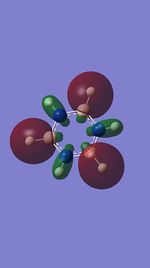
MO 13

The first set of MOs for comparison can be seen in the row labelled as "MO 13" (this is accurate for benzene, but not necessarily for the other 3 molecules). This set of MOs involve the s-orbitals of the C, B and N atoms, which have sigma overlap with the H(1s) orbitals and their neighbouring C/B/N 2s AOs. This supports the interesting observation that sigma MOs do also contribute to the aromaticity of these compounds. There is significant anti-bonding character in the benzene MO (MO 13), with antibonding interactions between neighbouring C atoms observed in the corresponding MO. While these antibonding sigma MOs are equally-sized (owing to the symmetry of benzene), boratabenzene's MO shows a large contribution by B, while pyridinium shows a small contribution by N. Meanwhile, in borazine, the N has a small contribution while the B atoms have a greater contribution. In contrast to benzene, these 3 compounds' MOs are polarised (the largest end of the MO in boratabenzene resides at the B atom, while the largest end of the MO in pyridinium is at the C atom para- to the N atom.

The larger contribution of the B atom in the MO (and N's diminished contribution) is due to the electropositivity of the B atom. The 2s AOs of B are hence higher in energy than the lower-lying 2s AOs of the electronegative N atom; hence, the B atoms contribute more significantly to the antibonding MO being discussed here. This is also observed in borazine, which shows larger contributions by the B atoms, and smaller contributions by the three N atoms.

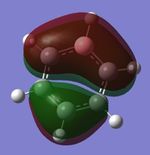
MO 21

The next set of MOs for discussion is found in the HOMO region of all 4 compounds. This analysis only focuses on one of the two degenerate MOs (e_1g symmetry in benzene) for benzene. This degeneracy in benzene is also observed in borazine; however, a loss of degeneracy is observed in boratabenzene and pyridinium (i.e. there is an energy splitting of the two MOs). This can be attributed to symmetry breaking due to introduction of a heteroatom (B or N), while benzene and borazine are symmetrical (hence the degeneracy of the 2 MOs is observed).

While MOs of the same shape and appearance are compared here, it must be noted that the MO for boratabenzene is the HOMO, while the MO for pyridinium is not the HOMO (it is HOMO-1). The MOs presented for boratabenzene and pyridinium hence have the same shape, but a re-positioning of energy levels is noted. This is attributed to the electronegativity of the N atom, which reduces the energy of this MO, hence it is the HOMO-1. (Conversely, the other MO of the originally-degenerate set of MOs is higher in energy in pyridinium; this is because the N (2p) orbital is non-bonding in that MO; hence, it is the HOMO.) In contrast, in the case of boratabenzene, the electropositivity of the B atom, coupled with the large B contribution, results in the raising of the energy of this MO; hence, the MO presented is the HOMO.

The MOs of boratabenzene and pyridinium are also polarised. It can be discerned that the larger contribution in each of the 2 MOs resides at the "electropositive" end of the aromatic molecule. In boratabenzene, B has the larger contribution, while in pyridinium, the largest contribution to the MO is located para- to the N atom. It is also note-worthy that the MOs in this region have some antibonding character, due to the presence of 2 nodal planes; hence, the electropositive B atom (with high energy AOs) has a larger contribution to the resulting MO, while the electronegative N atom (with lower energy AOs) has a smaller contribution to the MO, as observed. (A similar argument has been discussed above, for "MO 13")

Finally, in this series of MOs being compared, the borazine MOs appear to be similar to the benzene MOs. The borazine MOs are not polarised significantly (unlike pyridinium and boratabenzene), and appear to be similar to the benzene MOs. This could perhaps be attributed to the inherent symmetry of borazine and benzene; this is in contrast to boratabenzene and pyridinium (in which symmetry breaking is observedm resulting in ensuing polarisation of the MOs).

MO 16

This final set of MOs are selected for discussion, in spite of the difficulty in rationalising the size of the orbital contributions to the resulting MOs. An interesting feature of these row of MOs presented is the significant MO contributions seen in the ring itself; this could possibly be attributed to cluster bonding in the sigma framework itself. In addition, these MOs are particularly of interest in challenging the traditional concept of a "bond". A noticeable feature of these MOs is the through-space bonding interactions observed between the H atoms on the ring. For example, benzene's MO (MO 16) shows a set of bonding interactions between 3 H atoms on the ring, with another set of bonding interactions (out-of-phase to the first set!) on the other 3 H atoms in the ring. This reflects the delocalised nature of bonding as demonstrated by the MO. The involvement of quantum effects etc in computing these MOs hence suggest the limitations of the concept of "localised bonds" in molecules. MOs, as alluded to in the earlier section which discussed the definition of a bond, are hence a useful tool to describe the distribution of electron density, and the nature of bonding in these molecules.

Boratabenzene and pyridinium, in contrast to benzene, have polarised MOs, perhaps owing to the loss of symmetry (with the concomitant change in electron density of the resulting boratabenzene and pyridinium molecules, as suggested in the NBO bond analysis above). However, boratabenzene and pyridinium are polarised 'oppositely' - the largest contribution in boratabenzene resides at a region surrounding the B atom, while the largest contribution in pyridinium resides para- to the N atom substituent in pyridinium. It can be suggested that the electropositive 'end' of the molecule has the greatest contribution to the resulting MO; and the MO is hence polarised towards these electropositive 'sites'. This can be rationalised due to the discernible anti-bonding character of the MO, which also contains 3 nodes (in all of the 4 MOs presented in this section). The relatively electropositive B (in boratabenzene) and C (in pyridinium) atoms hence are higher in energy as AOs, and make a greater contribution to the MOs observed. As such, rotating either the pyridinium or boratabenzene MOs by 180 degrees will show that these two MOs share a great resemblance. Meanwhile, borazine's MO has a greater resemblance to benzene; however, surprisingly, borazine's MO is not perfectly symmetrical (unlike benzene). This is likely due to quantum effects; electronegativity arguments and the relative energies of the AOs are unlikely to be sufficient arguments which can rationalise this slight loss of symmetry in the MO of borazine. Nevertheless, it is reasonable to assert that this surprising shape of the borazine MO is due to the B-N bonds (in contrast to the C-C bonds in benzene); the perturbations and changes in the corresponding AOs which form the MOs could have resulted in the unsymmetrical MO for borazine. Another possible reason could be that the "top half" of the borazine ring involves 2 B atoms and 1 N atom, while the "bottom half" of the borazine ring consists of 2 N atoms and 1 B atom. This is in contrast to benzene, in which the top and bottom halves are identical (with 3 C atoms on the top and bottom face of benzene).

Brief Summary of MO Analysis

The substitution of the benzene ring by a heteroatom (B or N) resulted in unsymmetrical MOs, which are observed in pyridinium and boratabenzene. The polarised MOs, as evidenced by unequal contributions of the corresponding AOs to the eventual MOs, can be rationalised by the different electronegativities of the B and N atoms. This substitution by a heteroatom has resulted in a loss of symmetry and a loss of degeneracy, resulting in a energy splitting between MOs which are originally degenerate (in benzene). Upon the splitting of the energy levels, it is also evident that the relative ordering of these MOs differ (pyridinium v.s. boratabenzene); this depends on the shape of the MOs (does the heteroatom contribute to that particular MO, or is it non-bonding?) and the electronegativity of the heteroatoms (electronegative atoms lower the MO energies, while electropositive atoms raise the MO's energies). In general, the energies of the MOs of pyridinium were lower (N atom is electronegative), while those of boratabenzene were raised in energy (B atom is electropositive). Borazine was observed to have MOs which sometimes resembled the MOs of benzene, in terms of the MOs' shape, polarisation and energy - this is likely to be due to the symmetry inherent in borazine (higher D3h symmetry, as opposed to lowered C2v symmetry for boratabenzene and pyridinium); however, as is evident in the "MO 13" section, the differing electronegativity of the B and N atoms resulted in differing contributions to the MO observed. Interestingly, a comparative discussion of these MOs also allowed for an exploration of the delocalised nature of these MOs which sometimes involved through-space bonding interactions, in addition to features which suggested cluster bonding in the aromatic ring.

The substitution of benzene by a heteroatom is expected to affect the positioning of the energy levels in the full MO diagram. Substitution by an electropositive B atom would result in higher energy AOs (both the 2s and 2p will be raised in energy), which would explain the larger contribution of the B atom to MOs in the anti-bonding set, while the B atom would also contribute less to the eventual bonding MO. Substitution by a B atom is also likely to result in destabilisation in both the bonding and anti-bonding MOs; this has already been discussed in this section. Such destabilisation is attributed to the electropositivity of the B atom. It is likely that generating a MO diagram of benzene using LCAO principles will involve two separate "C₃H₃" fragments. These fragments are useful starting points in generating benzene's MO diagram; the degeneracy of these fragments is also a useful starting point. Hence, substitution of a C atom by a heteroatom will result in non-degenerate fragments; the interaction of these fragments orbital will be lessened, resulting in a smaller splitting energy of the bonding and anti-bonding MOs. The degenerate MOs which are seen in benzene will also not be observed in pyridinium and boratabenzene, due to the loss of symmetry in the molecule. These effects will also result in polarisation of the ensuing MOs; and the smaller splitting energy could also result in MOs which can mix, as they are closer together in energy.