User:Sw4512org
The Study of Reaction Products Using Molecular Mechanics and the Extraction of Spectroscopic Information via Quantum Mechanics
Introduction
The aim of this experiment is to develop an appreciation of the capability of computational organic chemistry by gaining familiarity with different softwares such as performing molecular mechanics calculation via the Avogadro interface and quantum mechanical density functional calculation using Gaussian, then performing analysis on the results obtained This includes energy comparisons, NMR data rationalisation, study of chiroptical properties of molecules and transition states.Firstly, the two different models used by the softwares- molecular mechanics and quantum mechanical density functional theory- is briefly introduced.
Molecular Mechanics
Molecular Mechanics (MM) is a classical method that neglects all the atomistic details of molecules and instead models nuclei and electrons as interacting hard spheres. And chemical bondings are modeled as springs of various elasticities. The energy is calculated as a sum of contributions from stretching, bending, torsional, Van der Waals and electrostatic energies. The actual way each of these contributing energy terms are calculated depends on the force field used. The force field is a composition of experimental parameters (such as equilibrium bond length, bond angle, etc) and proposed equations describing physical phenomena. In this study, the MMFF94s (Merck molecular force field for static processes) is used.
MM is a very computational cheap way to obtain data compared to quantum mechanical methods. But due to the lack of quantum mechanical detail, it is only used to look at relative energy differences between structures to determine relative stability, and relative contributions from each of the energy terms stated above. Electronic properties are not suitable for investigation using MM.
Density Function Theorem
The density functional theory (DFT) is an ab initio method that models the effect of electronic correlation by focusing on the electron density rather than the wavefunction and uses it to map out the energy. Self-consistently, a guess electronic density is inputted which gets refined after solving the Kohn-Sham equation at each iteration until convergence. In this investigation, the hybrid functional B3LYP formalism is used. Along with the model, a basis set is needed to construct the overall electron density. The 6-31G(d,p) basis set is used. The basis set is constructed using linear combination of atomic orbitals (LCAO), which are Slater type (hydrogenic) orbitals. The Gaussian software approximates these by multiplying Gaussian type orbitals, which reduce computation complexity due to the special property of Gaussian functions which multiply to give another Gaussian (so expensive multiplication can be simplified as adding powers).The naming conventions above means 6 Gaussian orbitals are used to construct the core atomic orbital basis set. While two valence atomic orbital basis sets are needed, with 3 Gaussian orbitals making up the first basis set, and 1 Gaussian orbitals to make up the other. The effect of d-type polarization functions to the basis set is included that in principle better simulate the electronic distribution in molecules.
Because this quantum mechanical method is closer to atomic reality, it is used to model transition structures, NMR and optical properties as well as molecular electronic topology.
Conformational analysis using Molecular Mechanics
All energy calculations reported are truncated to 5 d.p.
The Hydrogenation of Cyclopentadiene Dimer
The Diels-Alder reaction of cyclopentadienes is a [π4s + π2s] process that is capable of producing two products - endo and exo - with the former being the majority product [1]. This then can be mono-hydrogenated to give again two products, which are arbitrarily denoted ""hydrogenation product 1"" and ""hydrogenation product 2""" (see below). The exo and endo stable intermediates and two final products are studied in sequence using MM.
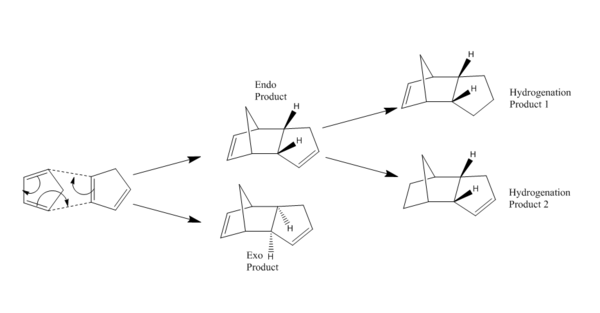
|
| Reaction Scheme |
|---|
Using the MMFF94s forcefield, the two dimerisation products were firstly optimised and presented below (second and third column). As stated before, the absolute magnitude of the energy reading is not meaningful, instead the relative magnitude is compared. The total energy indicates the exo product is more stable than the endo product.
It is given in the script the endo product is the only product. In order for the higher energy endo molecule to be the product, the reaction needs to be under kinetic control, meaning the dimerisation process irreversibility undergoes the endo transition structure, which is lower in energy than the exo transition structure and reaches the final product. The hypothesised kinetic controlled dimerisation is supported by literature findings where quantum mechanical transition state calculations performed using ab-initio computation methods using various basis sets were performed by Jorgensen et al. showing the endo transition structure is always lower in energy.[2]
From the energy breakdown, one can see the major difference in energy between the two molecules is from the angle bending energy.
| Exo product | Endo product | Hydrogenation product 1 | Hydrogenation product 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Jmol | ||||||||||||
| Total Bond Stretching Energy (kcal/mol) | 3.54300 | 3.46743 | 3.30837 | 2.82311
| ||||||||
| Total Angle Bending Energy (kcal/mol) | 30.77270 | 33.19066 | 30.86465 | 24.68517
| ||||||||
| Total Stretch-bending Energy (kcal/mol) | -2.04139 | -2.08218 | -1.92668 | -1.65717
| ||||||||
| Total Torsion Energy (kcal/mol) | -2.73102 | -2.94975 | 0.05894 | -0.37828
| ||||||||
| Total Out-of-plane Bending Energy (kcal/mol) | 0.01485 | 0.02197 | 0.01536 | 0.00028 | ||||||||
| Total Van der Waals Energy (kcal/mol) | 12.80162 | 12.35784 | 13.28120 | 10.63735
| ||||||||
| Total Electrostatic Energy (kcal/mol) | 13.01367 | 14.18472 | 5.12099 | 5.14702
| ||||||||
| Total Energy (kcal/mol) | 55.37344 | 58.19069 | 50.07228 | 41.25749 |
Using the same optimisation method, the endo product is subjected to hydrogenation at one of the two double bond site. The product with cyclo-pentene hydrogenated is denoted hydrogenation product 1 (column four above) while the one with norbornene double bond hydrogenated is denoted hydrogenation product 2 (column five above).
Experimental hydrogenation catalysed by SRNA-4 nickel alloy [3] indicates hydrogenation product 2 is easier to hydrogenate. As it is also lower in energy, this implies the reaction is under thermodynamic control, where crossing of the transition state is reversible and results in the most energetically stable product as the majority outcome. The energy breakdown shows the stabilisation for hydrogenation product 2 primarily comes from Van der Waals and angle bending interactions. The former can be qualitatively reationalised as after hydrogenation in the bigger ring (hydrogenation product 2) four new staggered conformations and two new eclipsed conformations are established around the vicinity of reaction. While hydrogenation in the smaller ring (hydrogenation product 1) two more staggered and two more eclipsed interactions are established. In a sense there is a gain in staggered interaction in product 2 and no gain in hydrogenation product 1. Angle bending can be qualitatively explained as in the bigger ring (hydrogenation product 2), when strain is relieved (by hydrogenation), there are more bonds that can adopt better conformation than there are in a smaller ring.
Atropisomerism in an Intermediate Related to the Synthesis of Taxol
Upon a multi-step synthesis of Taxol [4], a intermediate during the synthesis is isolated. Due to rotational strain it is possible to obtain two atropisomers (below) of this intermediate. As it has been discovered[5] that the reaction to reach this intermediate is reversible (thermodynamic condition), it is important to determine the lower energy isomer which will in turn be the major product.
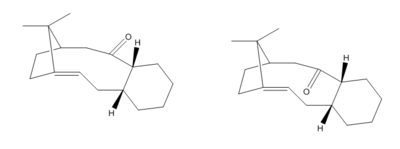
|
| Atropisomers of an intermediate during Taxol synthesis |
|---|
Before investigation on the intermediate can be undertaken, a naming convention needs to be established for ease of reference at later stages. The convention is as follows, if the dipole of the carbonyl group is aligned in the same direction as the bridging methyl group within the eight-membered ring, then this particular atropisomer is said to adopt the up conformation, while anti-aligned molecule is denoted down. For each of the atropisomers, there are substituents unsymmetrically distributed around the cyclohexane ring, resulting in two distinguishable chair conformer and two boat conformers that can assume energy minima. This results in a total of 8 different structures needing analysis. To further distinguish the two chairs and two boats that will form for each atropisomer, it is decided when the carbon (circled in green below) in the cyclohexane ring that is closer to the alkene functionality is pointing in the upward direction (again up is relative to the bridging methyl group), the consequent chair or boat conformer will be numbered 1. Conversely, if this particular carbon is pointing down, then the conforms will be numbered 2. To illustrate this naming system, the structure below on the left is up chair 1, while the one on the right is down boat 2
 |
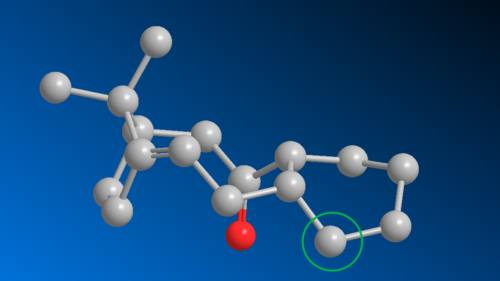
|
|---|---|
| up chair 1 | down boat 2 |
The table below shows the energy contributions for the four different conformer of the up atropisomer.
| Intermediate A (up) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Twisted Boat 1 | Twisted Boat 2 | Chair 1 | Chair 2 | |||||||||
| Jmol | ||||||||||||
| Total Bond Stretching Energy (kcal/mol) | 7.94775 | 8.00244 | 7.67267 | 8.22775
| ||||||||
| Total Angle Bending Energy (kcal/mol) | 29.69565 | 30.22872 | 28.26759 | 34.04495
| ||||||||
| Total Stretch-bending Energy (kcal/mol) | 0.09941 | -0.03609 | -0.07766 | 0.07349
| ||||||||
| Total Torsion Energy (kcal/mol) | 2.61550 | 2.68599 | 0.23951 | 3.64864
| ||||||||
| Total Out-of-plane Bending Energy (kcal/mol) | 0.95378 | 0.95719 | 0.98600 | 1.66122 | ||||||||
| Total Van der Waals Energy (kcal/mol) | 34.66062 | 35.80138 | 33.15496 | 34.78910
| ||||||||
| Total Electrostatic Energy (kcal/mol) | 0.31868 | 0.22920 | 0.29743 | 0.19973
| ||||||||
| Total Energy (kcal/mol) | 76.29140 | 77.93162 | 70.54050 | 82.64489 | ||||||||
For the up structure, the lowest energy conformer is chair 1. Looking into the specifics of the energy distribution, the low energy content is mostly due to the angle bending energy and the torsion energy comparing to the other three structures. Although for cyclyhexane, a chair is expected to have a lower energy than boat. But in this case the chair 2 structure has the highest energy content out of the four conformers. This can be partly explained as the boats optimised actually assumes a slightly twisted structure, which lowers their respective energy contents. Additionally, chair 2 has by far the largest angle bending and out-of-plane bending energy, meaning high strain is suffered to assume this structure.
The table below shows the energy contributions of the four conformers for the down atropisomer.
| Intermediate B (down) | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Twisted Boat 1 | Twisted Boat 2 | Chair 1 | Chair 2 | |||||||||
| Jmol | ||||||||||||
| Total Bond Stretching Energy (kcal/mol) | 7.79383 | 7.75327 | 8.66163 | 7.58865
| ||||||||
| Total Angle Bending Energy (kcal/mol) | 21.24496 | 19.02340 | 21.82979 | 18.81421
| ||||||||
| Total Stretch-bending Energy (kcal/mol) | -0.05966 | -0.13238 | -0.19520 | -0.14175
| ||||||||
| Total Torsion Energy (kcal/mol) | 4.44638 | 3.75328 | 6.14934 | 0.23156
| ||||||||
| Total Out-of-plane Bending Energy (kcal/mol) | 0.93208 | 0.95053 | 1.63871 | 0.84317 | ||||||||
| Total Van der Waals Energy (kcal/mol) | 34.56384 | 35.00274 | 36.22957 | 33.26869
| ||||||||
| Total Electrostatic Energy (kcal/mol) | -0.04521 | -0.06235 | 0.41927 | -0.05411
| ||||||||
| Total Energy (kcal/mol) | 68.87622 | 66.28850 | 74.73312 | 60.55042 | ||||||||
For the down structure, the lowest energy conformer is changed from chair 2 to chair 1, the former now assumes the highest energy. Again, torsion energy and angle bending energy seems to play important roles. Additionally Van der Waals seems to play a important role as well.
An interesting pattern is observed. When the cyclohexane end closer to the carbonyl group and the C=O bond are pointing in opposite directions (the two end points from which all the angle measurements are presented in the table), energy of that conformer is lower than if the two groups point in the same direction. This is observed as up chair 1 is lower in energy than up chair 2, while down chair 2 is lower in energy than down chair 1. The same is seen for the boat structures.
It was first thought that by enforcing the two groups to point in the same direction, the ring junction is very locally distorted and consequently increases the torsion and bond bending energy. However, one can see from the angle measurements in the table that for both chair and boat 1&2 structures the angle is roughly the same. In the case of the up chairs, the more distorted (away from the ideal sp3 109.5°) up chair 1 is actually lower in energy than up chair 2. If there is no significant change locally, then this implies when the aforementioned two groups pointing in the same direction, the reminder parts of the molecule adopts a more strained form and perhaps small amounts of bond bending/torsion accumulates within the eight-membered ring and causes a raise in overall energy.
Comparing the lowest energy structure from up and down, down chair 2 is significantly more stable than up chair 1 (by about 10 kcal/mol). This difference can almost exclusively be accounted for by the angle bending energy. As in this case both structures have the carbonyl and cyclohexane carbon defined above pointing in opposite directions, this implies the relative orientation of the methylene group in the oct-member ring and carbonyl group is important.
Hyperstable Alkene
It is stated in the script that the alkene functional group from the above molecules reacts very slowly which contradicts with theory[6]. To investigate this phenomena, optimisation using MMFF94s forcefield is run on the lowest energy down chair 2 structure (denoted alkene) and its hydrogenated version (denoted alkane below).
| Alkane | Alkene | |||||
|---|---|---|---|---|---|---|
| Jmol | ||||||
| Total Bond Stretching Energy (kcal/mol) | 6.42175 | 7.58865
| ||||
| Total Angle Bending Energy (kcal/mol) | 22.28351 | 18.81421
| ||||
| Total Stretch-bending Energy (kcal/mol) | 0.29379 | -0.14175
| ||||
| Total Torsion Energy (kcal/mol) | 9.20418 | 0.23156
| ||||
| Total Out-of-plane Bending Energy (kcal/mol) | 0.03894 | 0.84317 | ||||
| Total Van der Waals Energy (kcal/mol) | 31.29324 | 33.26869
| ||||
| Total Electrostatic Energy (kcal/mol) | 0.00000 | -0.05411
| ||||
| Total Energy (kcal/mol) | 69.53538 | 60.55042 |
The relative energies of both structure shows that hydrogenation is thermodynamically unfavoured by almost 10 kcal/mol. The alkene is favoured primarily due to small torsion energy and angle bending energy. This hyperstability of ring junction alkene is supported by the work of Maier et al [7].
Spectroscopic Simulation using Quantum Mechanics
In this part of the study, the carbon and hydrogen NMRs of a thiol derivative of the intermediates studied above was computed. This was done using B3LYP/6-31G(d,p) via Gaussian and adding the keyword phrase ""opt scrf(cpcm,solvent=chloroform) freq(vcd) NMR EmpiricalDispersion=GD3"". The same convention for up and down as well as 1 and 2 as before was adopted and the up isomer is arbitrarily chosen for the NMR study. Even though it was later found the down isomer actually contains the lowest energy conformer. This means if reaction to reach these pair of molecules is again reversible like before, it would be more meaningful to investigate the down isomer instead.
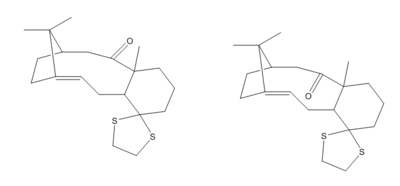
|
| Derivatives of the Taxol intermediate studied above |
|---|
The solvent is kept as chloroform, for which both carbon and hydrogen NMR literature data is attained [8]
Each of the structure was drawn in ChemBio3D and imported into Avogadro and subjected to optimisation using MMFF94s force field (see the Total Energy from MM row below). The optimised structures were then submitted to the high performance cluster for quantum mechanical calculations. For Gaussian calculations where the energy is requested, the unit is converted from Hatrees to kcal/mol (see the Free Energy from DFT row below).
| Up | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Conformer | Chair 1 | Chair 2 (twisted) | Boat 1 | Boat 2 | ||||||||
| Jmol | ||||||||||||
| Total Energy from MM (kcal/mol) | 104.78692 | 118.01969 | 125.56113 | 120.36236 | ||||||||
| DOI | DOI:10042/195235 | DOI:10042/195236 | DOI:10042/195246 | DOI:10042/195247 | ||||||||
| NMR |  |
 |
 |
| ||||||||
| NMR |  |
 |
 |
| ||||||||
| Free Energy from DFT(kcal/mol) | -1036307.76401 | -1036307.76401 | -1036293.22461 | -1036293.22461 | ||||||||
It is observed that for the free energy obtained for the two chairs are identical, the same is true for the boats. This was at first thought to be peculiar, because the potential energy surface for a molecule of such size and complexity should not be so regular (put it in another way, these identical energies obtained suggests a degree of symmetry in the potential energy surface that is unfounded when inspecting the connectivity of the molecule). However, it was later realised that the MM optimised conformers underwent conformational change during the DFT calculation. In each case, the lower (MM calculated) energy conformer in the chair & boat pair was reached during the DFT calculation and its NMR was generated. Thus the free energies were found to be the same. Consequently, structures with the same free energies produced the same NMR spectra.
All four conformer share the same labeling order, which is presented below.
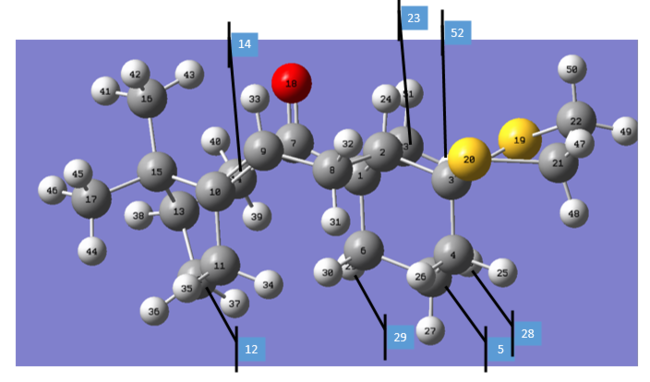
The outcomes of the NMR calculation are tabulated:
| 13C NMR Chemical Shift Results (ppm) | ||||
|---|---|---|---|---|
| Atom | Chair | Boat | Literature[8] | |
| 7 | 206.398 | 204.758 | 218.79 | |
| 10 | 135.424 | 139.673 | 144.63 | |
| 9 | 114.988 | 107.209 | 125.33 | |
| 3 | 80.943 | 81.565 | 72.88 | |
| 2 | 50.935 | 54.849 | 56.19 | |
| 1 | 47.341 | 50.624 | 52.52 | |
| 15 | 42.773 | 44.311 | 48.50 | |
| 13 | 41.842 | 43.148 | 46.80 | |
| 21 | 36.990 | 37.928 | 45.76 | |
| 14 | 36.247 | 36.925 | 39.80 | |
| 22 | 32.468 | 34.486 | 38.81 | |
| 4 | 30.870 | 30.362 | 35.85 | |
| 6 | 25.616 | 23.470 | 32.66 | |
| 8 | 21.306 | 23.166 | 28.79 | |
| 12 | 19.633 | 21.755 | 28.29 | |
| 23 | 19.633 | 20.981 | 26.88 | |
| 11 | 17.389 | 17.658 | 25.66 | |
| 17 | 16.698 | 17.163 | 23.86 | |
| 5 | 13.199 | 12.352 | 20.96 | |
| 16 | 10.022 | 11.860 | 18.71 | |
| boat | Literature Value(ppm)[8] | chair | ||
|---|---|---|---|---|
| Atoms | Shift (ppm) | Atoms | Shift (ppm) | |
| 33 | 5.669 | 4.84 | 33 | 5.286 |
| 47 | 3.585 | 3.40-3.10 | 50 | 3.443 |
| 48 | 3.502 | 49 | 3.356 | |
| 50 | 3.413 | 24 | 3.294 | |
| 31 | 48 | 3.150 | ||
| 49 | 3.123 | 2.99 | 47 | |
| 32 | 2.80-1.35 | 34 | 2.851 | |
| 34 | 2.979 | 31 | ||
| 24 | 2.815 | 43 | 2.770 | |
| 38 | 2.483 | 40 | 2.532 | |
| 35 | 2.389 | 39 | ||
| 26 | 32 | |||
| 25 | 26 | |||
| 40 | 36 | 2.409 | ||
| 36 | 2.101106945 | 35 | ||
| 39 | 2.023 | 38 | 2.257 | |
| 27 | 30 | |||
| 28 | 1.942 | 25 | 2.090 | |
| 30 | 1.851 | 28 | 2.039 | |
| 43 | 1.711 | 52 | 1.881 | |
| 44 | 1.653 | 1.38 | 44 | 1.731 |
| 51 | 1.382 | 37 | ||
| 53 | 1.330 | 27 | ||
| 46 | 1.189 | 1.25 | 29 | 1.625 |
| 37 | 51 | 1.300 | ||
| 52 | 1.103 | 46 | 1.043 | |
| 41 | 1.012882963 | 1.1 | 45 | |
| 29 | 42 | |||
| 45 | 0.849 | 41 | 0.959 | |
| 42 | 0.705 | 1.00-0.80 | 53 | 0.727 |
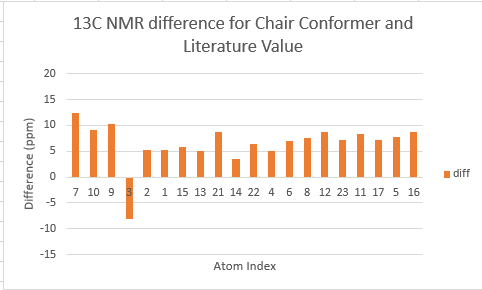
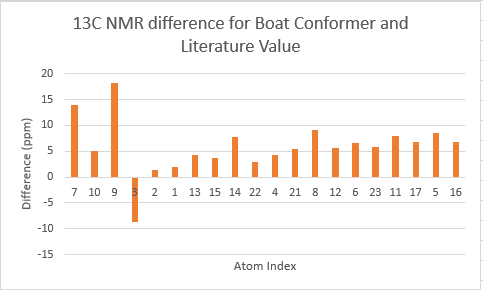
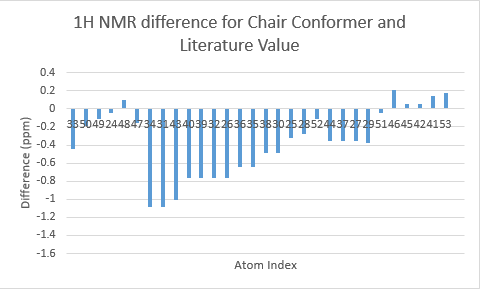
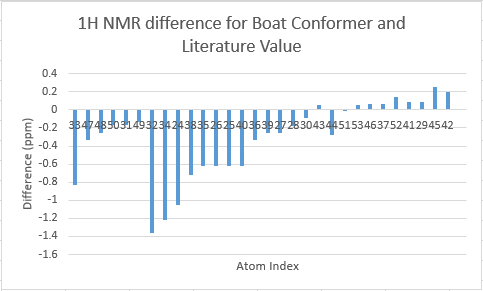
The two tables above are summarised into the following plots, where the difference between literature values and calculated values are plotted against the atom number. In determining the results for proton NMR, chemical shifts of methyl and methylene protons are averaged and for literature values with a range, the middle value is taken.
 |
|
 |
|
Looking at the tables and the spectra, it makes sense that the highest carbon shifts are for the carbonyl carbon C7, alkene carbon C9 & C10 as well as the S-C-S carbon C3 where there are significant deshielding. While for the proton NMR, the highest chemcial shift signal is the the proton bonded to the alkene, which is the most deshielded proton while all the other proton environments are in the aliphatic region without significant deshielding agent nearby.
The deviation of calculated C3 value from the literature can be explained because of the proximity of the heavy sulphur atoms, which causes spin-orbit coupling that leads to calculation error. Similarly, the deviation can be resolved for C21 and C22. The deviations observed for the latter are smaller than for the former. This can be explained because C3 is one bond away from two sulphur atoms, resulting in larger spin-orbit couplings, whereas C21 and C22 only has one sulpur one bond away. Similarly, the deviation can be explained for C7, which is the carbonyl carbon.
Comparing the carbonyl carbon C9 of the two conformations, one can observe for the boat structure the deviation is the largest amongst all the presented differences. The significant deviation could be an indication that the boat structure used for the calculation is more conformationally varied to the actual sample from which NMR spectrum was obtained. This hypothesis is further supported as for both the proton and carbon NMR, the boat conformer shows a generally greater deviation than the chair conformer (the vertical scale of plots have been set to the same range for ease of comparison). In terms of the deviation for the proton NMR, the most pronounced differences come from proton environments in the cyclohexane ring, indicating the NMR sample structure differ the most within the cyclohexane conformation to the computed structures.
The down isomer was also optimised and submitted for NMR calculation. The free energy generated are presented below, but due to time constraint detailed NMR analysis was not performed on it. One can see the free energy for chair 1, boat 1 and boat 2 are the same, suggesting conformational change had occurred, most probably all three changed to the lowest energy boat 2 conformer. Overall, down chair 2 is the most energetically stable atropisomer.
| Down | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Conformer | Chair 1 | Chair 2 | Boat 1 | Boat 2 | ||||||||
| Jmol | ||||||||||||
| Total Energy from MM (kcal/mol) | 105.55504 | 100.43765 | 102.31498 | 102.22221 | ||||||||
| DOI | DOI:10042/195244 | DOI:10042/195241 | DOI:10042/195245 | DOI:10042/195243 | ||||||||
| Free Energy from DFT (kcal/mol) | -1036307.48352 | -1036309.64905 | -1036307.48352 | -1036307.48352 | ||||||||
Analysis of the Properties of the Synthesised Alkene Epoxides
Two asymmetric catalysts are studied in this section. The Jacobsen catalyst, published in 1991 for asymmetric epoxidation of alkenes [9] and the Shi catalyst also for asymmetric epoxidation of trans-alkenes and tri-substituted olefins discovered in 1996 [10]. The structure of the salen catalysts (precursors to the active species) are studied first, following which the NMR and optical properties calculations of epoxide products using each of the catalysis schemes are conducted. The study culminates with energetic and electronic analysis of the epoxidation transition states.
Catalyst Strucutrues
The salen species for the Shi catalyst was found on the PubChem Compound Database. The compound (formal name: 1,2:4,5-Di-O-isopropylidene-beta-D-erythro-2,3-hexodiulo-2,6-pyranose) has a CID: 18422-53-2. While the salen precursor to Jacobsen catalyst was found on the ConQuest Database using the molecular formula C36H52ClMnN2O2. The TOVNIB01 structure was chosen for further investigation. Both compound was visualised using the program Mercury. In the case of Jacobsen catalyst, one unit of the catalyst was deleted, leaving only one unit for the analysis below for ease of visualisation.
Jacobsen Catalyst
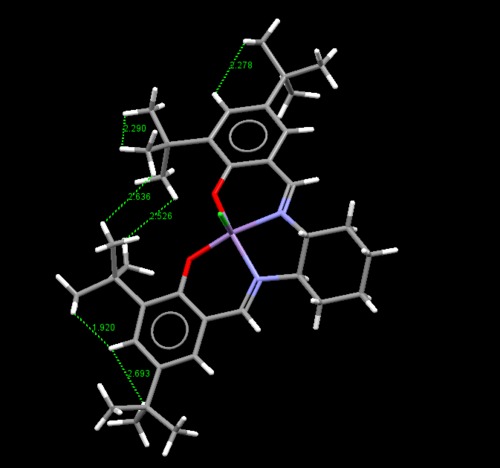
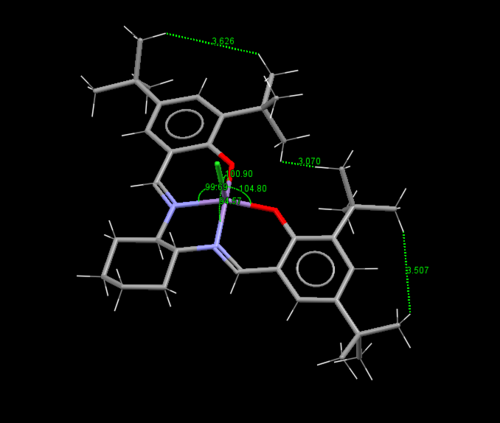
The Van der Waals radius of hydrogen is 1.2 Å [11]. Starting with the leftmost figure, one can see many of the hydrogenic interactions at the tert-butyl substituents come very close to double the hydrogen Van der Waals of 2.4 Å, where repusive interaction will begin to dominate. One can also see interactions between the t-butyl and hydrogen on the benzene ring being smaller than 2.4 Å. This can be summarised as high degree of steric hinderance on the left side of the molecule is blocked for approach of the reagent.
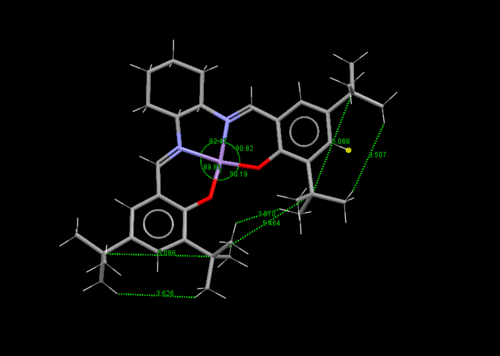
The center and rightmost figures show the bond angles at the square pyramidal metal center, with the chloride (which will be changed to an oxygen in the active species) as the tip. In the center figure, one can see for the four base groups of the pyramid, a distorted larger bond angle of 90.19° is established between the O-C-O moiety, this is presumably to reduce the repulsive interaction between the t-butyl groups. The rightmost figure measures the angle between the chloride tip and the four bases of the pyramid. One can see larger angles for the two bases (104.80° and 100.90°)closer to the t-butyl group. This pushes the t-butyl groups further away from the reaction center (where the chloride currently resides), again presumably to reduce unfavourable interaction.
 |
 |
|
Shi Catalyst
The anomeric effect describes the tendency of a heteroatomic substituent adjacent to a heteroatom to reside in the axial position of a cyclohexane ring. This is because of favourble overlap of bonding and anti-bonding orbitals due to the anti-periplannar orientation. For the Shi catalyst, all the C-O bond length were labeled except the C=O group (C10, O6) and presented below. One can see there is only one six-membered ring, where O2 can exhibit the anomeric effect into O4 through C8, conversely O4 can do the same into O2 again via C8. This better orbital overlap should results in bond shortening. This shortening is observed where other bonds have a bond length greater than 1.43 Å.
However, the shortest C-O bond in the system is between O1 and C7 which resides in the five membered ring, where this acetal group do not have the required geometry to allow the anomeric effect to occur. Further observation shows that this oxygen is almost in the eclipsed conformation with the carbonyl group. It could be the case that lone pair on O1 can donate its electron density into the carbonyl via the planar framework (akin to conjugated alkene system) and therefore the charge delocalisation results in bond shortening.

The calculated NMR properties of products
The structure of the epoxidation stereoisomers are presented with their NMR properties tabulated. As before, the molecules were first optimised using MMFF94s and then subjected to DFT (B3LYP) calculation, 6-31G(d,p) basis set with the ""scrf(cpcm,solvent=chloroform) freq(vcd) NMR EmpiricalDispersion=GD3"" keyword phrase was used. The solvent was kept as chloroform for which literature values have been attained.[12] In determining the plots below, chemical shifts of methyl and methylene protons are again averaged and for literature values with a range, the middle value is taken.
Stilbene oxides are presented first:
| S,S-Stilbene Oxide | R,R-Stilbene Oxide | ||||
|---|---|---|---|---|---|
 |
| ||||
| DOI:10042/195240 | DOI:10042/195239 | ||||
| NMR | |||||
 |

| ||||
| NMR | |||||
 |
| ||||
| Calcualted Value | Literature Value[12] | 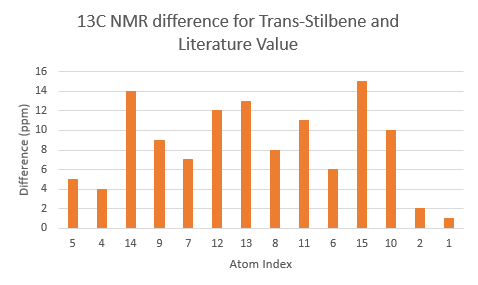
|
|---|---|---|
| 124.382 | 137.7 | |
| 124.382 | 137.7 | |
| 114.515 | 129.1 | |
| 114.515 | 129.1 | |
| 113.813 | 128.8 | |
| 113.813 | 128.8 | |
| 113.508 | 128.8 | |
| 113.508 | 128.8 | |
| 113.374 | 128.8 | |
| 113.374 | 128.8 | |
| 108.559 | 126.1 | |
| 108.559 | 126.1 | |
| 56.72 | 63.3 | |
| 56.72 | 63.3 |
| Calcualted Value | Literature Value [12] | 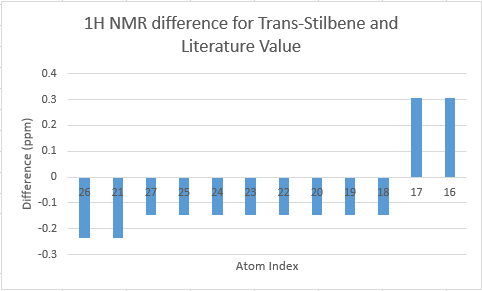
|
|---|---|---|
| 7.706 | 7.42–7.52 | |
| 7.706 | 7.42–7.52 | |
| 7.615 | 7.42–7.52 | |
| 7.615 | 7.42–7.52 | |
| 7.615 | 7.42–7.52 | |
| 7.615 | 7.42–7.52 | |
| 7.615 | 7.42–7.52 | |
| 7.615 | 7.42–7.52 | |
| 7.615 | 7.42–7.52 | |
| 7.615 | 7.42–7.52 | |
| 3.673 | 3.98 | |
| 3.673 | 3.98 |
The NMR data obtained are identical for the two isomers. This is expected as stereoisomers should only differ in optical (and biological) properties. However, the deviation between literature and computed value is still quite large, this is especially true for the aromatic carbon and protons. This might be due to strong intermolecular π–π stacking in solution phase which alters the electronic properties of the aromatic region. Such intermolecular interaction is not included in single molecular DFT calculation.
Dihydronaphalene oxides are presented as follow:
| R,S-1,2-Dihydronapthalene Oxide | S,R-1,2-Dihydronapthalene Oxide | ||||
|---|---|---|---|---|---|
|
| |||||
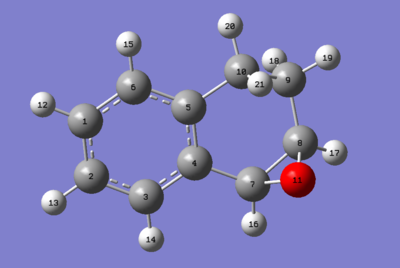 |
| ||||
| DOI:10042/195237 | DOI:10042/195238 | ||||
| NMR | |||||
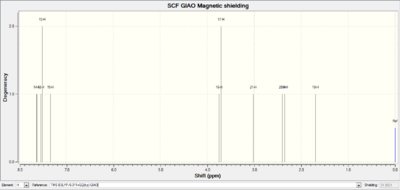 |
| ||||
| NMR | |||||
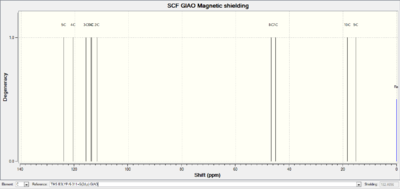 |
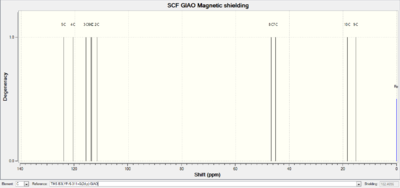
| ||||
| Calcualted Value | Literature Value [12] | 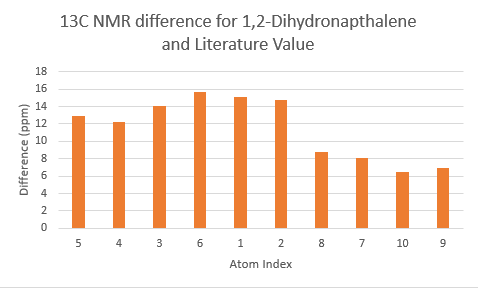
|
|---|---|---|
| 124.1373 | 137.1 | |
| 120.679 | 132.9 | |
| 115.848 | 129.9 | |
| 114.1308 | 129.8 | |
| 113.7204 | 128.8 | |
| 111.7367 | 126.5 | |
| 46.729 | 55.5 | |
| 45.12417 | 53.2 | |
| 18.33161 | 24.8 | |
| 15.24076 | 22.2 |
| Calcualted Value | Literature Value [12] | 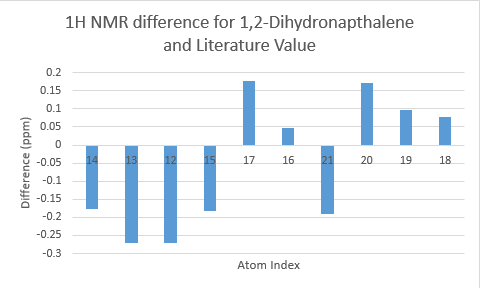
|
|---|---|---|
| 7.626236627 | 7.45 | |
| 7.522080147 | 7.35–7.20 | |
| 7.522080147 | 7.35–7.20 | |
| 7.331131433 | 7.15 | |
| 3.723632408 | 3.90 | |
| 3.723632408 | 3.77 | |
| 3.01604874 | 2.85–2.80 | |
| 2.403607563 | 2.60–2.55 | |
| 2.352149306 | 2.50–2.40 | |
| 1.698658613 | 1.80–1.75 |
Again, the NMR spectra for both isomers are identical. And the largest deviations come from aromatic carbons and hydrogens.
An interesting observation from all the NMR calculations performed is the apparent bias for computed carbon NMR data to be smaller than literature value (most of the orange bars are in the first quadrant) while for the proton NMR the computed values are systematically bigger than literature values, resulting in most of the blue bars to be in the fourth quadrant. A brief survey of the literature yields no plausible explanation as to where possible parametrisation within the calculation results in this bias. The lack of such information seems to suggest this has not been observed in calculations performed by others.
Assigning the absolute configuration of the product
Optical Rotation
To obtain the desired data, the stilbene oxides and dihydronaphalene oxides products were first separately conformationally optimised using MMFF94s, then the optical rotation of these epoxide were calculated quantum mechanically via CAM-B3LYP mehtod with the 6-311++g(2df,p) basis set. the keyword pharse ""polar(optrot) scrf(cpcm,solvent=chloroform) CPHF=RdFreq"" was included in the .com file. The optical rotation was calculated at both 365 nm and 589 nm. Although literature values for 365 nm in chloroform were not found.
| S,S-Stilbene Oxide | R,R-Stilbene Oxide | ||||||
|---|---|---|---|---|---|---|---|
| DOI:10042/195332 | DOI:10042/195329 | ||||||
| Computed value at 365 nm | Computed value at 589 nm | Literature value at 589 nm | Computed value at 365 nm | Computed value at 589 nm | Literature value at 589 nm | ||
| -1247.41° | -219.78° | -258.1°[13] | 1235.45° | 227.17° | 256.1 °[13] | ||
| R,S-1,2-Dihydronapthalene | S,R-1,2-Dihydronapthalene | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| DOI:10042/195326 | DOI:10042/195325 | ||||||||
| Computed value at 365 nm | Computed value at 589 nm | Literature value at 589 nm | Computed value at 365 nm | Computed value at 589 nm | Literature value at 589 nm | ||||
| -633.86° | -183.16° | -138.8°[13] | 631.78° | 182.63° | 135.3°[13] | ||||
Theoretically, the optical rotation for a pair of stereoisomers should have the exact same magnitude, but the opposite signs. However, in reality as one can see the literature values for an isomeric pair differ in the first digit. This is presumably affected by the limit of measurement accuracy and the extent of isomer purity.
In terms of the computed values, one can see that firstly the difference in the absolute values between pairs of isomer is larger than the difference in literature values, usually differing in the second digit. This is because each of the isomer was optimised separately using MM and each reached a different local conformational minimum. As the isomers do not have the same conformation (which they do in reality if the solvent is not chiral when subjected to the same physical conditions), their optical rotation value differ by more.
Secondly, comparing computed values to the literature values, the signs agree in all cases. Additionally, as the magnitude of optical rotation is greatly affected by the conformation, the rather small differences (less than 50° in all cases, which is less than 15% of one rotation) is acceptable in the author's opinion.
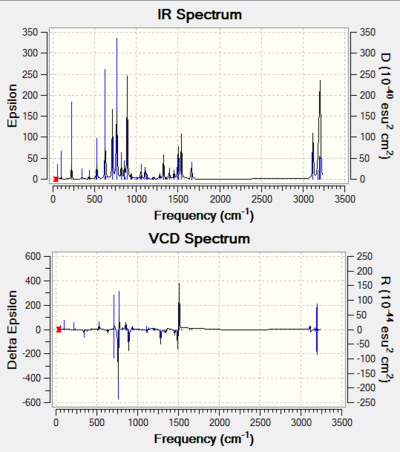
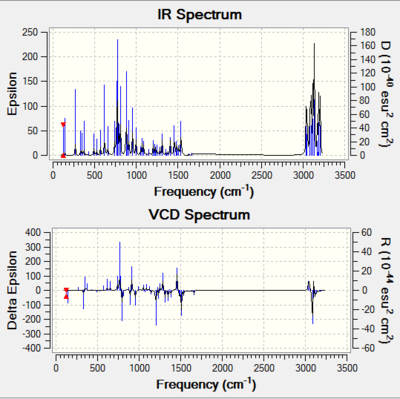
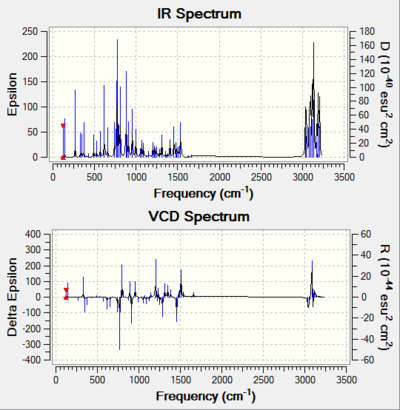
Vibrational Circular Dichroism
In this section, the Vibrational Circular Dichroism (VCD) is presented along with the IR spectrum. VCD provides 3D structural information about a molecule as it can detect the relative orientation of groups in the molecule, meaning chirality can be deduced from VCD. For two separate chiral molecules, the VCD spectra should be exact opposite of one another.
One can see for each pair of isomers, their VCDs are reflections of one another along the horizontal axis. This supports they are stereoisomers. And the presence of the identical IR spectra simply show the two molecules have the same functional groups, which further supports they have the same chemical properties, implying they are indeed stereoisomers.
| S,S-Stilbene Oxide | R,R-Stilbene Oxide |
|---|---|
| DOI:10042/195330 | DOI:10042/195331 |
 |
|
| R,S-1,2-Dihydronapthalene | S,R-1,2-Dihydronapthalene |
|---|---|
| DOI:10042/195328 | DOI:10042/195327 |
 |
|
Transition State Analysis
The enantiomeric excess (ee) measures the purity of chiral compounds. It is mathematically defined as:
where R and S are the relative fraction of each of the two enantiomer. The relative fractions of R and S can be obtained from the equilibrium constant K for the interconversion between S and R (S ⇋ R). K for the forward reaction is as below:
Substituting the above relation to the ee equation one can obtain the following:
To obtain K, one can invoke the relationship between K and the change in free energy:
Δ
ΔG in this case measures the difference between the free energy of the two isomers' transition state. This is why all possible transition states of the alkene with the catalyst need to be found and the lowest energy transition state needs to be selected for the aforementioned analysis. For the free energies data presented below, the lowest energy is highlighted in green. Temperature was chosen as 293 Kelvin in the calculations.
Transition Structure of Shi Catalyst with Stilbenes
| Transition states for Shi epoxidation of Stilbene | |||
|---|---|---|---|
| R,R series | S,S Series | ||
| DOI | Free Energy (kcal/mol) | DOI | Free Energy (kcal/mol) |
| DOI:10.6084/m9.figshare.828552 | -963031.34484 | DOI:10.6084/m9.figshare.829524 | -963028.60388 |
| DOI:10.6084/m9.figshare.830388 | -963030.99595 | DOI:10.6084/m9.figshare.829525 | -963029.63864 |
| DOI:10.6084/m9.figshare.829522 | -963039.01866 | DOI:10.6084/m9.figshare.830389 | -963035.11618 |
| DOI:10.6084/m9.figshare.829523 | -963038.93332 | DOI:10.6084/m9.figshare.830390 | -963033.88626 |
The energy units were converted to J/mol before proceeding with calculating the value of K and the ee value that is to follow. The difference was calculated by doing the R-isomer subtracting the S-isomer.
| ΔG (J/mole) | K | Calculated ee(%) | Literature ee(%) |
|---|---|---|---|
| -16327.97632 | 814.36234 | 99.8 | 83[14] |
Transition Structure of Shi Catalyst with Dihydronaphthalenes
| Transition states for Shi epoxidation of Dihydronaphthalene | |||
|---|---|---|---|
| R,S series | S,R Series | ||
| DOI | Free Energy (kcal/mol) | DOI | Free Energy (kcal/mol) |
| DOI:10.6084/m9.figshare.832492 | -866666.56055 | DOI:10.6084/m9.figshare.832538 | -866673.185802 |
| DOI:10.6084/m9.figshare.832510 | -866669.76336 | DOI:10.6084/m9.figshare.832536 | -866663.622556 |
| DOI:10.6084/m9.figshare.832511 | -866674.89200 | DOI:10.6084/m9.figshare.832545 | -866669.853726 |
| DOI:10.6084/m9.figshare.832512 | -866670.28796 | DOI:10.6084/m9.figshare.832544 | -866676.254324 |
Energy difference here was taken by the R,S-isomer subtracting the S,R-isomer.
| ΔG (J/mole) | K | Calculated ee(%) | Literature ee(%) |
|---|---|---|---|
| 5699.96362 | 0.09635 | 82.4 | 32 [15] |
Transition Structure of Jacobsen Catalyst with Stilbenes
| Transition states for Jacobsen epoxidation of Stilbene | |||
|---|---|---|---|
| R,R series | S,S Series | ||
| DOI | Free Energy (kcal/mol) | DOI | Free Energy (kcal/mol) |
| DOI:10.6084/m9.figshare.899176 | -2243297.38463 | DOI:10.6084/m9.figshare.903625 | -2243298.58506 |
| ΔG (J/mole) | K | Calculated ee(%) | Literature ee(%) |
|---|---|---|---|
| 5022.59912 | 0.12724 | 77.4 | 25[16] |
Transition Structure of Jacobsen Catalyst with Dihydronaphthalenes
| Transition states for Jacobsen epoxidation of Dihydronaphthalene | |||
|---|---|---|---|
| R,S series | S,R Series | ||
| DOI | Free Energy (kcal/mol) | DOI | Free Energy (kcal/mol) |
| DOI:10.6084/m9.figshare.909346 | -2146935.86716 | DOI:10.6084/m9.figshare.903752 | -2146941.94082 |
| DOI:10.6084/m9.figshare.907332 | -2146935.958149 | DOI:10.6084/m9.figshare.907473 | -2146937.26399 |
| ΔG (J/mole) | K | Calculated ee(%) | Literature ee(%) |
|---|---|---|---|
| 25031.49546 | 3e-05 | 100.0 | 85[17] |
It is observed the calculated and literature values agree quite well in the case of transition structure of Shi catalyst with stilbenes and of Jacobsen catalyst with dihydronaphthalenes. Additionally the calculated values are systematically larger than literature ones. The difference is mostly due to the computational incapability to accurately determine energy minima of transition states for such large system sizes at a reasonable computational cost.
Non-Covalent Interactions
The non-covalent interactions (NCI) are interactions which are relatively weak in strength such as hydrogen bonds, Van der Walls interactions and electrostatic attractions. The Shi catalyst with R,R-Stilbene transition state was chosen to be studied. It was mapped by downloading the .fchk file available at this DOI:10.6084/m9.figshare.832511 and visualised using Gaussview.
In the figure generated, only two types of interactions are present, coded in green and yellow. The former means mild attractive interactions and the latter mildly repulsive interactions. It can be seen the amount (in terms of area) of attractive interactions greatly outweight repulsive ones. This is somewhat expected, because if the opposite is true the two molecules will be driven away from one another and no reaction would occur, meaning this would not be a transition state.
The top part of the figure is the catalyst, and the bottom parts of the figure is the stilbene species lying flat. It is observed the benzene rings on the reagent does not seem to be interacting with the catalyst in the NCI fashion at all. The major interaction comes from interactions between the fructose rings and the aliphatics of the stilbene very close to the reaction center.
Important interactions that aids the formation of the transition state are pointed out below.

QTAIM
The same system is chosen as before here. The electronic topology of the system is mapped using Avogadro2 and the .wfn file downloaded at the DOI:10.6084/m9.figshare.832511 , via the Molecular graph drop-down in Extension/QTAIM (QTAIM stands for Quantum Theory of Atoms in Molecules). Yellow points between any two purple points indicate a bond critical point (BCP). Yellow points on solid lines indicate covalent interaction, when on dashed line it means the interaction is non-covalent.
One can see all the BCP for covalently bonded hetreoatoms (C-H, C-O) have the BCP at a position that reflects the relative eletropositivity of the hetroatoms (in C-H bond the yellow point is closer to H, in C-O closer to C). However, between all non-covalent interactions, BCPs always resides at the middle (at least qualitatively).
As there is a point of symmetry in the stilbene reagent, one can split the alkene into two halfs. The figure below pinpoints some important non-covalent BCPs that aids the crossing of transition state to form the epoxide product.

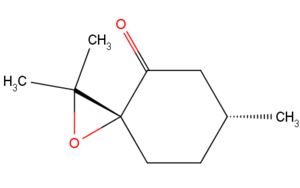
New Candidate for Investigation
Cis R-(+)-pulegone oxide is suitable candidate to undergo the computational investigation above. It has a CAS registry number of 7599-91-9 and a molecular weight of 168.236 g/mol. The alkene precursor (R)-(+)-pulegone is readily available in the Sigma Aldrich catalog, with a CAS number of 89-82-7, and successful epoxidation process has been recorded in the literature [18]. The optical property measured in ethanol at 25 °C and 324 nm wavelength light is reported as 853.9°.[19]
References
- ↑ J. E. BALDWIN, J. Org. Chem., 1966, 31 (8), 2441. DOI:10.1021/jo01346a003
- ↑ William L. Jorgensen , Dongchul Lim , James F. Blake., "Ab initio study of Diels-Alder reactions of cyclopentadiene with ethylene, isoprene, cyclopentadiene, acrylonitrile, and methyl vinyl ketone", J. Am. Chem. Soc., 1993, 115 (7), pp 2936–2942DOI:10.1021/ja00727a021
- ↑ Ji-Jun Zou, Xiangwen Zhang, Jing Kong, Li Wang (2008). Fuel 87: 3655–3659. doi: 10.1016/j.fuel.2008.07.006DOI:10.1016/j.fuel.2008.07.006
- ↑ S. W. Elmore and L. Paquette, Tetrahedron Letters, 1991, 319; DOI:10.1016/S0040-4039(00)92617-0
- ↑ S. W. Elmore and L. Paquette, Tetrahedron Lett., 1991, 32 (3), 319. DOI:10.1016/S0040-4039(00)92617-0
- ↑ J.Bredt, Liebis Ann, 1924, 437 (1), pp. 1-13 DOI:10.1002/jlac.19244370102
- ↑ Wilhelm F. Maier, Paul Von Rague Schleyer (1981). "Evaluation and prediction of the stability of bridgehead olefins". J. Am. Chem. Soc. 103(8): 1891–1900. DOI:10.1021/ja00398a003
- ↑ 8.0 8.1 8.2 Leo A. Paquette, et al. (1981). "[3.3] Sigmatropy within 1-vinyl-2-alkenyl-7,7-dimethyl-exo-norbornan-2-ols. The first atropselective oxyanionic Cope rearrangement". J. Am. Chem. Soc. 112(1): 277–283. DOI:10.1021/ja00157a043
- ↑ W. Zhang, E. N. Jacobsen, J. Org. Chem., 1991, 56 (7), 2296. DOI:10.1021/jo00007a012 10.1021/jo00007a012
- ↑ Tu, Y.; Wang, Z.-X.; Shi, Y. J. Am. Chem. Soc. 1996, 118, 9806-9807. DOI:10.1021/ja962345g
- ↑ Batsanov, S. S. "Van der Waals radii of elements." Inorganic materials , 2001: 871-885. DOI:10.1023/A:1011625728803
- ↑ 12.0 12.1 12.2 12.3 12.4 M.W.C Robinson, K. S. Pillinger, I. mabbett, D. a.a Timms, A.E. Graham, tetrahedron, 2010 66(43), pp. 8377-8382 DOI:10.1016/j.tet.2010.08.078
- ↑ 13.0 13.1 13.2 13.3 Z. Wang,Y. Tu,M. Frohn,J. Zhang and Y. Shi Journal of the American Chemical Society 1997 119 (46), 11224-11235. DOI:10.1021/ja972272g
- ↑ Yian Shi, et al. (2009). "Asymmetric Epoxidation Catalyzed by α,α-Dimethylmorpholinone Ketone. Methyl Group Effect on Spiro and Planar Transition States". J. Org. Chem. 74(16): 6335–6338. DOI:10.1021/jo900739q
- ↑ M. Frohn, Y. Shi, Synthesis, 2000, 14, 1979-2000
- ↑ Paola Piaggio, et al. (2000). "Enantioselective epoxidation of (Z)-stilbene using a chiral Mn(III)–salen complex: effect of immobilisation on MCM-41 on product selectivity". J. Chem. Soc., Perkin Trans. 2, missing volume(10): 2008-2015.DOI:10.1039/B005752P
- ↑ J. Hanson, J. Chem. Educ., 2001, 78(9), 1266-1268, DOI:10.1021/ed078p1266
- ↑ Bogár, K. (2005). Oxidation of α-methylstyrene on an MCM-22 encapsulated (R, R)-(−)-N, N′-bis(3,5-di-tert-butylsalicylidene)-1,2-cyclohexanediaminocobalt(II) catalyst. Open Chemistry, 3(1), pp. 63-71. Retrieved 13 Mar. 2015, from DOI:10.2478/BF02476238
- ↑ William Reusch , Calvin Keith Johnson, J. Org. Chem., 1963, 28 (10), pp 2557–2560 DOI:10.1021/jo01045a016.
