User:Sw4512

The Study of Transition Structures of Pericyclics Reactions

The study of transition structure (TS) allows the characterisation of reaction pathway and activation energy and thus gives valuable insight to the evolution of chemical reactions. An alternative to experimentally capturing the transition state via techniques like femtosecond spectroscopy is to solve the quantum mechanical dynamics of the system via computational means. A calculation producing observables concordant to experimental data can then be used to model similar systems and thus be used to make predictions. The TS study of specific cases of two classes of pericyclic reactions is presented here, namely that from sigmatropic rearrangement and cycloaddition.

Essentially, a reaction is a positional change upon a potential energy surface (PES). The reactant(s) and product(s) reside at the local (at the rare case the global) minima on the potential energy surface. A path connecting the reactant and product is described as the reaction pathway. Such pathway will have a point of highest potential energy reached, and the molecular configuration corresponding to this point is called the transition structure. A feasible transition structure represents a point of maximum with respect to the reaction path, but with respect to the PES, it should also be a point of minimum along every other direction but the reaction path, thus ensuring the highest energy that the reaction is required to take place is as low as possible (What if we consider quantum tunneling effect through the potential energy barrier? João (talk) 21:05, 22 December 2014 (UTC)). This is a very elaborated way of saying a TS represents a saddle point upon a PES. On a complicated PES, more than one saddle point can arise for a reaction. Though given the reaction is under kinetic control, only the TS with the lowest energy will be crossed.

The Gaussian 09 software package is used to carry out the numerical calculations and GaussView 5.0 is used as the visualising tool. The types of calculations conducted are briefly described here:

Opt

Optimisation takes in an initial configuration (gjf file) as input and probes the potential energy surface to find coordinates where the derivative of the PES is zero (using iterative methods such as stochastic gradient descent). In the case of optimising to a minimum, the algorithm finds a local minima on the PES, and this usually corresponds to one of the low energy conformer of the input structure.

The situation is more complex if optimisation to a transition structure (optimise to TS(Berny)) is requested, where the second derivative of the potential energy is calculated with respect to all the coordinate variables. A transition structure is the point of highest energy along a reaction path, which means the second derivative at a TS point is negative (meaning a maxima) along the reaction coordinate. Additionally, the second derivative along every other coordinate varible should be positive (meaning minima). The output gives a configuration that satisfies the two criteria (One can check by looking at the vibrational modes of the structure, only one of the frequencies should be negative). To optimise to a minimum is far cheaper than to a TS, as the former calculation only involves travelling downhill (first derivative) against the steepest valley until there is no direction to descent towards. Whereas the latter requires constant checking of the second derivative.

In the case of optimise to TS(QST2), two input files are needed, one of the reactant(s) and the other the product(s). The algorithm tries to interpolate between these two input and tries to work out a saddle point that links them together. Probing of the entire potential surface is computationally forbidden, therefore the optimised structure will almost exclusively be local optima (unless the system under study is extremely simple like atomic head-on collision) that are closest to the input structure in the coordinate space.

Freq

The job carries out a frequency analysis, which gives all the vibration modes the structure possesses. This is instrumental to check if a minimization job indeed culminated with a structure with all positive frequencies and a TS optimisation indeed finished with all but one negative frequency. It also calculates among other things the thermochemical properties, which can be compared to those measured from experiments. The ones investigated in later section includes:

- the sum of electronic and zero-point energies, the electronic energy plus vibrational energy at absolute zero

- the sum of electronic and thermal energies, the electronic energy plus translational, vibrational and rotational contributions at standard condition

- the sum of electronic and thermal enthalpies, this adds an addition RT term to the expression above

- the sum of electronic and thermal free energies, this additionally considers entropic contribution.

Often Opt+Freq has been used to combine the two sequential job as one.

IRC

Internal reaction coordinate is used to trace backward and/or forward the reaction pathway from the input transition structure, giving the configurations of the starting material and ending product as outputs.

Limitations in the computational capabilities (both in hardware and algorithm) as well as theoretical infeasibilities mean simulations cannot replicate the complication of nature in its fullest form. To reduce computational burden, only molecules needed to undergo one particular reaction is acquired, neglecting any secondary intermolecular and solvent interactions. The reaction is assumed to take place in vacuum. Solving the wave equation in its exact analytical form for systems of interest is infeasible. Several models have been used that make simplifications to give numerical solution are briefly introduced below.

Methods

HF

The Hatree Fock method makes the assumption a many-electron wavefunction can be approximated by the product of the individual 1-electron wavefunctions (neglecting electronic correlation). The overall wavefunction takes into account of anti-symmetry of the electron wavefunction by summing over all possible electron pair permutations. The wavefunction can be transformed into a Slater determinant and solved in an iterative manner by first providing an guess to the wavefunction and solve the Hatree-Fock equation to get a new approximation of the wavefunction. Convergence is achieved when the change in wavefunction between iteration is below a certain pre-set threshold. Throughout the calculation the charge distribution needs to be unchanged, or be self-consistent.

Semi-empirical

A semi-empirical scheme adopts the Hatree-Fock formalism, but estimates many of the integral calculations by using experimental and spectroscopic data, and using empirical rules to set certain overlap integrals to zero. This approach greatly reduces the computational complexity. Different empirical rules and spectroscopy database will yield different results. In this exercise the AM1 scheme is chosen and it is used to determine the molecular orbital (MO) distributions.

DFT

It is easy to see the neglect of electronic correlation in HF could be an issue. The density functional theory better models such effect by focusing on the electron density rather than the wavefunction and uses it to map out the energy. Self-consistently, a guess electronic density is inputted which gets refined after solving the Kohn-Sham equation at each iteration until convergence. The hybrid functional B3LYP formalism is used here.

Basis Sets

With the ab initio methods (DFT and HF), one needs to specify a basis set that is used to construct the overall wavefunction or electron density. The basis set is constructed using linear combination of atomic orbitals, which are Slater type (hydrogenic) orbitals. The program Gaussian approximates these Slater orbitals by multiplying Gaussian type orbitals, which reduce computation complexity due to the special property that Gaussian functions multiply to give another Gaussian (so expensive multiplication can be simplified as adding powers).

Two basis set are used for the ab initio methods in this exercise: 3-21G and 6-31G*. The naming conventions 'x-yzG' means x Gaussian orbitals are used to construct the core atomic orbital basis set. While two valence atomic orbital basis sets are needed, with y Gaussian orbitals making up the first basis set, and z Gaussian orbitals to make up the other. The extra asterisk means the addition of d-type polarization functions to the basis set that can in principle better simulate the electronic distribution in molecules.

Conformations of 1,5-hexadiene Generated Using HF/3-21G
Conformation	Point Group	Energy (hartree)	Relative Energy (kcal/mol)	Jmol
Gauche 1	C2	-231.687716	3.102912
Gauche 2	C2	-231.691667	0.623681
Gauche 3	C1	-231.692660	0.000000
Gauche 4	C2	-231.691530	0.709436
Gauche 5	C1	-231.689615	1.910872
Gauche 6	C1	-231.689160	2.196746
Anti 1	C2	-231.692602	0.036841
Anti 2	Ci	-231.692535	0.078909
Anti 3	C2h	-231.689071	2.252914
Anti 4	C1	-231.690971	1.060704

Cope Rearrangement

Cope rearrangement is a special class of sigmatropic rearrangement, namely [3,3] rearrangement constituting only carbon atoms. The numbers in the square bracket corresponds to positions where the new σ bond will be formed, with the count starting at the positions where the old σ bond will be broken. The prototypical Cope rearrangement with no substituent is presented below and its conformers as well as its transition structure, of which it has two as shown, will be studied.

Reactants/Products

1,5-hexadiene has three C-C bond that can freely rotate. With three possible staggered conformers around each of the three bonds, this in principle results in 3³ = 27 conformations. However, due to the symmetry around the middle C-C bond, the number of unique conformation is reduced to 10, 6 gauche and 4 anti-periplanar, which from now on is abbreviated as anti. Using HF/3-21G level of theory, minimization calculations have been run for the conformers and a comparison of the absolute and relative energy across them is presented on the right. As the requested convergence on energy matrix is only to 10e-06, the energy terms are all rounded to the sixth decimal place.The point groups as well as the energies are in accordance with those enlisted in the instruction appendix 1.

The conversion factor between hartree and kcal/mol is 1 hartree = 627.509 kcal/mol.

K_BT is ~0.5 kcal/mol at ambient temperature. Looking at the table, this means many of the conformers could be isolated at room temperature. One would also expect the lowest energy conformer should adopt anti around the central C-C bond to minimise steric clash, but counter-intuitively HF/3-21G predicts the gauche 3 form to have the lowest energy. This is a manifestation of the favourable interaction between the π orbitals and the vinyl protons .

The anti 2 structure is studied further by reoptimising using B3LYP/6-31G*. The following table presents the geometric differences between anti 2 using the two methods. Only half of the molecule needs to be analysed due to the molecule having a center of inversion. The notation C(u-v-w-x) corresponds to the dihedral angle between the labelled carbon atoms. C(a-b) means the shortest distance between carbon a and b, "-" and "=" differentiates single and double bonds. This notation is carried through in this exercise.

Gemometry Comparison of Anti 2 Structure Using HF and DFT
	HF/3-21G	B3LYP/6-31G*
Dihedral angle (°) C(1-2-3-4)	114.62606	118.57644
Dihedral angle (°) C(2-3-4-5)	180.00000	180.00000
Bond Length (Å) C(1=2)	1.31618	1.33350
Bond Length (Å) C(2-3)	1.50882	1.50420
Bond Length (Å) C(3-4)	1.55317	1.54816

The geometric differences predicted by these methods is minute, with bond length only differing by a few pm. The biggest change is the dihedral angle between C(1-2-3-4) and C(3-4-5-6), meaning the terminal carbons are now pointing further away from one another.

Lastly, a Frequency job is run on the B3LYP/6-31G* anti 2 structure. All vibrations are positive, confirming this structure is at an energy minimum. The energy readings are obtained from the outputted log file. By default, the energies corresponds to measurables at 298.15 K. By including an extra keyword temperature=0.01 these measurables at close to 0 K can be deduced. One can see the sum of electronic and zero-point energies equals at the two temperatures as expected. Additionally, at near 0 K the only sources of energy is the ground state electronic energy and the zero-point residue vibrational energy. Therefore the values in all the rows for the 0 K column are equivalent.

Thermochemical Data
	0 K	298.15 K
Sum of electronic and zero-point energies	-234.469216	-234.469215
Sum of electronic and thermal energies	-234.469216	-234.461865
Sum of electronic and thermal enthalpies	-234.469216	-234.460920
Sum of electronic and thermal free energies	-234.469216	-234.500805

Chair & Boat Transition Structure

Three methods are explored in this section to study the chair and boat transition structure. To optimise the chair, two CH₂CHCH₂ fragments are drawn on top of one another and with the fragment pointing in opposite directions. (like that shown in 'Chair TS Optimised using B3LYP/6-31G*'). After setting the intermolecular distance between the terminal carbons to 2.2 Å, the structure is selected to optimise to TS(Berny) using Opt+Freq with HF/3-21G. Force constant is calculated once and the additional keyword opt=noEigen needs to be included.

Another approach to find the transition structure uses the same fragments but with Opt=ModRedundant instead. In essence, this method involves first freezing the bond making and breaking geometry as stationary and optimise (to minimum) the reminder molecule so the fragments are at a energetically relaxed state. Then by unfreezing the bond making/breaking process, an optimisation ( to TS(Berny)) should again yield the transition structure using HF/3-21G. By performing the first step of this second method, the guessed transition structure can often resemble more of the actually TS after relaxation and therefore allow a cheaper calculation with a guessed force matrix. While the first method requires the force matrix to be at least calculated once, which could be expensive.

The two method converged to the same TS structure with a same negative frequency (-817.92 cm^-1 for former and -817.89 cm^-1 for latter). The bond distance between terminal carbons on opposite fragment is 2.02 Å (smaller than the guessed 2.20 Å in method 1) and the bond angle between the three carbons consisting the allylic fragment is 120.5°.

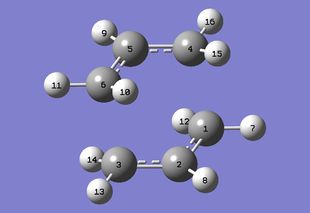
The boat transition structure is optimised using QST2. The optimised anti 2 structure from the previous section is used as the reactant and product, and by renumbering the atoms in the molecules as below (compare Reactant Numbering column with Product Numbering column), the atomic rearrangement due to the broken and formed σ bonds is taken into account. This structure can then be fed into Gaussian via OPT+Freq and HF/3-21G, choosing to optimise to TS(QST2) this time.

The output of this job interestingly gives a seemingly chair transition state and it gives very similar negative frequency to the one obtained before (-817.17 cm^-1). The error is deduced upon examining the TS with numbered atoms. The predicted TS in the first row below indicates the it is perhaps reached from the reactant by elongating the C(3-4) bond to the extent that C(1-6) begin to show bonding character. This goes against one's chemical intuition because this unnecessarily requires the molecule to be at a very high vibrational quantum level, when the same bond forming and breaking process can be achieved by a single rotation about C(3-4), which the algorithm seems to overlook (This is simply an algorithm issue. The algorithm has no knowledge of chemistry: you asked for a transition state, it gives you one. João (talk) 21:05, 22 December 2014 (UTC)). Thus the algorithm is helped by inputting a modified version of anti 2 in the second row (C(2-3-4-5) dihedral angle to 0°. C(2-3-4) and C(3-4-5) bond angle to 100°). The boat transition structure is obtained with one negative frequency at -840.07 cm^-1.

Frozen Coordinate Method (Not sure you mean that João (talk) 21:05, 22 December 2014 (UTC))
	Reactant Numbering	Predicted TS	Product Numbering
Using anti 2 as reactant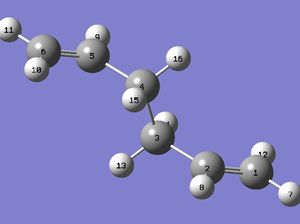
Corrected anti 2 gemometry to give gauche conformer (Would you still call it anti? João (talk) 21:05, 22 December 2014 (UTC))

It is curious to see which conformer has led to the boat transition structure. Therefore the modified input structure above is optimsed using the same level of theory to a minimum (Was this an IRC or a normal optimization calculation? A normal optimization does not necessarily follow the reaction coordinate. João (talk) 21:05, 22 December 2014 (UTC)). It turns out gauche 3, the lowest energy conformer, is the reactive conformer. But is the lowest energy conformer always the reactive conformer? To answer this an IRC calculation is run on the chair TS obtained before using the same level of theory. Calculation converged in 64 steps. The conformer obtained is the gauche 2 structure. One can see from the IRC output gauche 2 is structurally the closest to the chair TS, one can perhaps say the same for the gauche 3 in the boat case. The reactive conformer does not need to be the lowest energy conformer, but it is likely to be the conformer with the most structural resemblance with the TS. (Can you define a sufficiently generic criteria to structural resemblance? João (talk) 21:05, 22 December 2014 (UTC))

Chair TS IRC

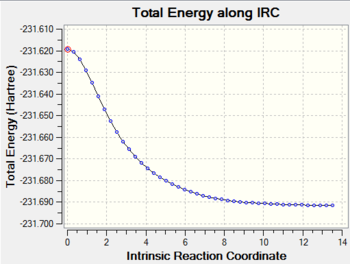
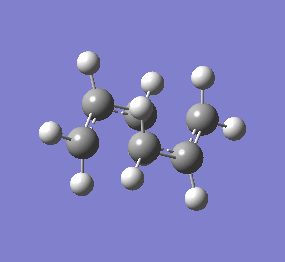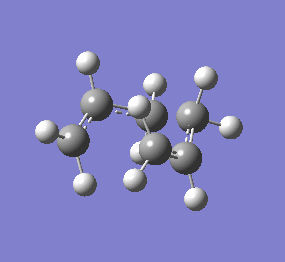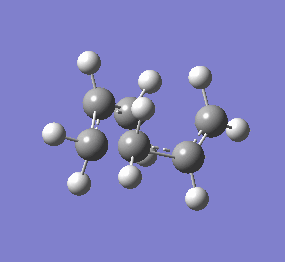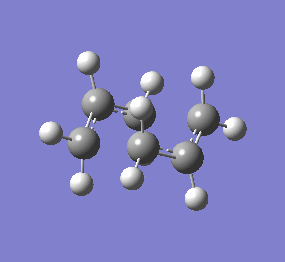
The figure below shows the negative vibrational mode for the boat and chair structure corresponding to the reaction. Bond forming and breaking is synchronised in both cases. The jmol file shows the TS calculated using higher level B3LYP/6-31G*. From the optimised TS, one can see the hydrogens on the terminal carbons on the two allyl fragment can adopt a staggered conformation in the chair TS while they are eclipsed in the boat TS. This means the two fragments in the chair structure can approach one another closer than in the boat case and therefore lowering the necessary energy of reaction.

Chair & Boat TS Geometries
Chair Transition State	Chair TS Optimised using B3LYP/6-31G*	Boat TS Optimised using B3LYP/6-31G*	Boat Transition State

Opt+Freq is performed on the boat, chair transition structures and the conformers gauche 2 (the product of chair IRC), anti 2 (of which experimental data of activation energy to both TS exists) using HF/3-21G and B3LYP/6-31G*. The thermochemical data obtained is reported below. The drop in energy when using the B3LYP/6-31G* set is in good accordance with the variational principle (Do you expect DFT with B3LYP functional to obey the variational principle? João (talk) 21:05, 22 December 2014 (UTC)), which states the energy calculated approaches the true energy with better approximated wavefunction (via a more accurate basis set here) and the energy expectation value will never be less than the true energy.

Energies Summary (hartree)
	HF/3-21G			B3LYP/6-31G*
	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies	Electronic energy	Sum of electronic and zero-point energies	Sum of electronic and thermal energies
		at 0 K	at 298.15 K		at 0 K	at 298.15 K
Chair TS	-231.619323	-231.466698	-231.461338	-234.556931	-234.414908	-234.408980
Boat TS	-231.602802	-231.450928	-231.445299	-234.543079	-234.402356	-234.396012
Reactant (Anti 2)	-231.692535	-231.539539	-231.532566	-234.611711	-234.469215	-234.461865
Reactant/Product From IRC (Gauche 2)	-231.691667	-231.538704	-231.531794	-233.33525	-233.191888	-233.184622

The following table presents the activation energy of Cope rearrangement from the anti 2 structure using HF/3-21G and B3LYP/6-31G* level of theory against experimentally determined data provided. One can see a good correspondence between the B3LYP/6-31G* calculation and experiment.

Activation Energy with Anti 2 as Reactant(kcal/mol)
	HF/3-21G	HF/3-21G	B3LYP/6-31G*	B3LYP/6-31G*	Expt.
	at 0 K	at 298.15 K	at 0 K	at 298.15 K	at 0 K
ΔE (Chair)	45.708383	44.696211	34.078131	33.185813	33.5 ± 0.5
ΔE (Boat)	55.604200	54.760828	41.954624	41.323350	44.7 ± 2.0

The values contained in the two tables above are concordant with those given in appendix 2 in the script.

Diels Alder Cycloaddition

Diels Alder .is a special class of cycloaddition reaction, namely [4+2] cycloaddition. The numbers in the square bracket corresponds to the number of π electrons participating in the reaction from each of the two fragments. The one with 4 π electrons is termed diene, the one with 2 π electrons is often denoted the dienophile. The prototypical Diels Alder reaction with no substituent is presented below. Its single transition structure will be characterised.

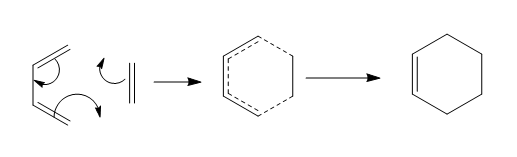
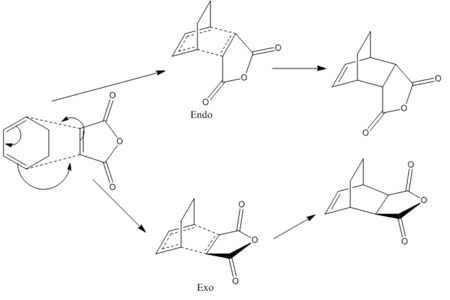
Then the discussion moves to the reaction between cyclohexa-1,3-diene and maleic anhydride (below). An attempt is made to analyse the two different TS of the adduct that leads to two distinct products.

The section will terminate with a brief discussion with regard to two aspects that the study of Diels Alder here has overlooked.

Reaction of Ethene and Butadiene

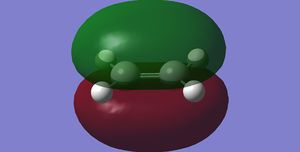
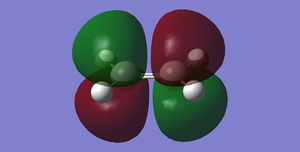
Cis-butadiene and ethene are optimised to energy minima using the semi-empirical AM1 method separately. The outcome structures possess the MO presented below. With respect to the plane mirroring the left and right of the molecule, cis-butadiene has an antisymmetric HOMO and a symmetric LUMO. While the other reactant, ethene, has symmetric HOMO and antisymmetric LUMO with respect to the plane defined in the same manner.

Reactants Frontier Orbital Diagram
	cis-Butadiene	Ethene
HOMO
LUMO

On its way to the product, one can deduce the optimal orbital overlap is between the antisymmetric LUMO of the ethene with antisymmetric HOMO of butadiene to give total constructive interference. If the opposite set of (symmetric) orbitals were to interact instead, there will be considerable destructive interference. (Not really, overlap of the two symmetric orbitals will be significant (albeit dependent on the approaching direction). João (talk) 21:05, 22 December 2014 (UTC))

Modifications

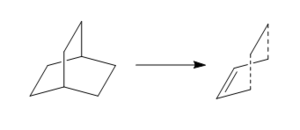
To elucidate the transition structure, the ring fragment bicyclo[2,2,2]octane is used from the template file. The following diagram shows the modifications needed. A hydrogen count is advised before proceeding. After using the clean tool, optimisation to TS(Berny) using Opt+Freq is applied to the structure using two methodologies: i) using semi-empirical AM1 ii) using HF/3-21G optimisation followed by optimisation by B3LYP/6-31G*. The second method consumes far more cpu time than the former.

The van der Waals radius of carbon is 0.170 nm, its typical sp³ bond length determined by X-ray diffraction is 0.154 nm. Correspondingly 0.133 nm for sp² bonds. Comparing these values to the calculations of various bond length in the TS (below left), the original three double bonds in both the diene and dienophile have become slightly extended by almost the same amount (to ~0.139 nm) as the p-orbitals interacts to make the two new σ bonds. But this extension is small compared to the contraction of the single bond on the diene, which shortens by more than 10 pm (compared to literature C-C single bond) as it transforms to a double bond. This can be explained as the π-bonds on the diene have p-orbital already aligned in the correct way to accommodate the forming of the new π-bond, only shift in electron density is required and the ease with which this bond can form is reflected in the larger change in bond length. Whereas for the double bonds to become single bonds, the p-orbitals need to reorientate themselves first before transferring electron density.

It is anticipated the dashed bonds should be much longer than data book C-C bonds as they have not been fully formed yet. But they are much shorter than twice the van der Waals radii of carbon, indicating there is sufficient electronic interaction and orbital overlap between the diene and dienophile at the transition state.

TS Geometry
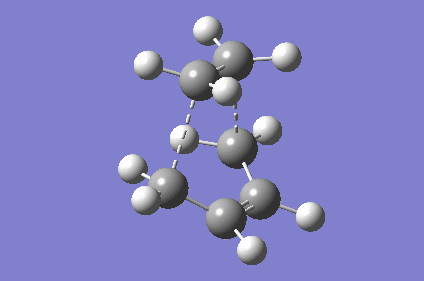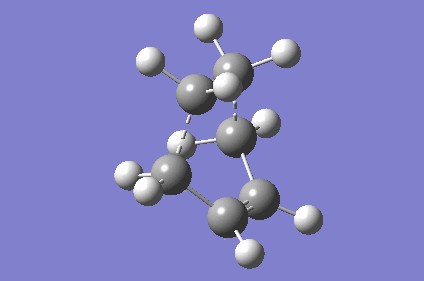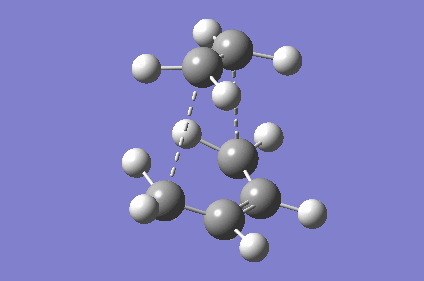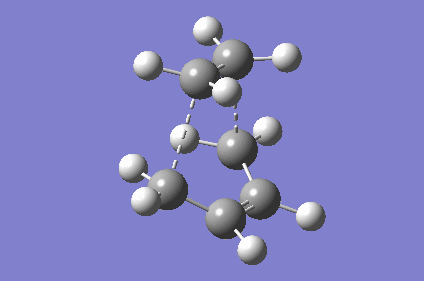
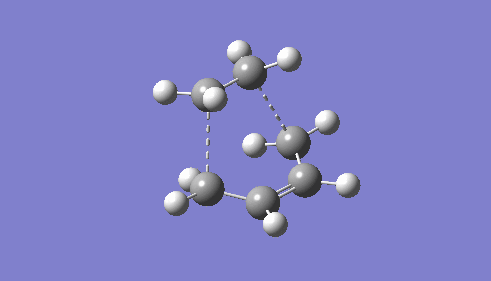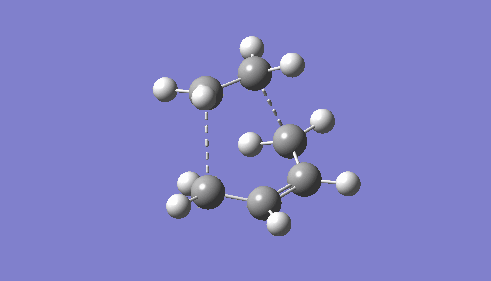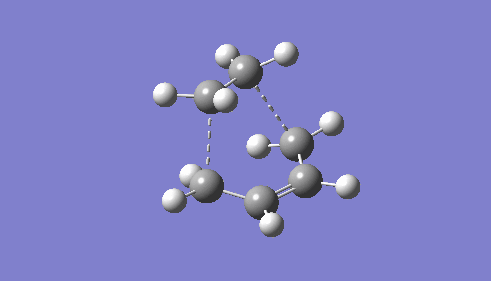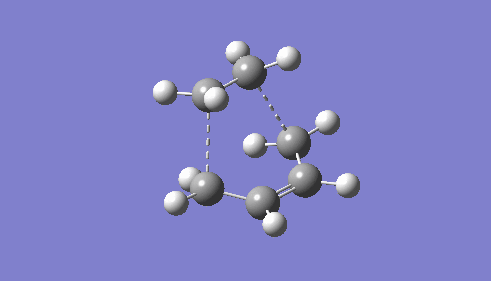
TS Bond Length B3LYP/6-31G*	TS Imaginary Frequency	TS Lowest Real Frequency

The vibration mode leading to the product (middle) shows the bond forming process is synchronous. The new bonds form suprafacially on both molecule, leading to a _π4_s component interacting with a _π2_s component. Such system is symmetry allowed under the Woodward-Hoffmann rule for thermal pericyclic reactions because the total number of (4n+2)_s and (4m)_a components is odd, where n and m are integers. (the total is 1 at this case as there is no antarafacial component).

The synchronicity allows the transition structure to contain [4+2] π electrons that approaches a planar fashion, thus satisfying (4n+2) Huckel aromaticity that leads to stability of the TS and hence it is favoured compared to asynchronous bond formation. This is in good accordance with experimental findings.To name a few, exceptionally high negative entropy is observed for cycloadditions to occur, because the concertedness require good alignment of both bonds simultaneously, which very small fraction of available molecular states can achieve. The rate of reaction also does not depend highly on the type of solvent, because the concertedness means no ionic or radical intermediate is generated and thus solvent stabilisation is almost negligible.

The rightmost animation shows the vibrational mode with the lowest positive frequency. It is an orthogonal vibration mode to the negative frequency vibration. The animation proves it is not aiding the bond formation process as such a positive frequency vibration mode is not along the reaction pathway.

TS Frontier Orbitals
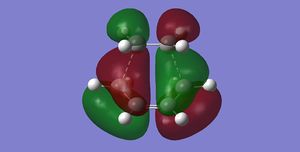
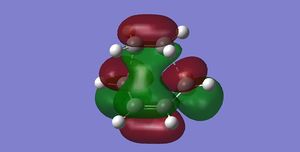
HOMO	LUMO

The frontier orbitals presented here has been calculated using semi-empirical AM1 method, with the HOMO being antisymmetric and LUMO symmetric with respect to the mirror plane. One can easily spot the resemblance between the antisymmetric HOMO orbital of the TS and the antisymmetric reactants HOMO/LUMO pair that are used to construct it. (But also the LUMO results from the combination (mostly anti-bonding) of the symmetric frontier orbitals of the reactants João (talk) 21:05, 22 December 2014 (UTC))

TS HOMO from B3LYP/6-31G*

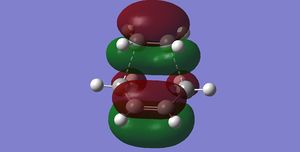As is mentioned, the TS has also been calculated using B3LYP/6-31G*. Contrary to the above finding, the HOMO in this case exhibits symmetry about the mirror plane. This orbital picture is flawed as analysis above shows the symmetric pair of reactant frontier orbitals combine with large anti-bonding character and thus should be unfavoured (Unfavoured in which respect? Did you look at the HOMO-1 orbitals? Isn't this just an issue of relative orbital energies? João (talk) 21:05, 22 December 2014 (UTC)). Therefore, one should be cautious when interpreting MO generated using B3LYP/6-31G*, despite it being more computationally expensive and being reliant on ab initio calculations rather than interpolation from experimental data.

Numerous attempts to produce the cyclohexene product by running IRC has failed to converge and resulted in errors before the algorithm takes the second step. It has not been resolved even with demonstrator's help. Although running the IRC in the forward direction results in convergence and the desired starting materials are obtained.

IRC

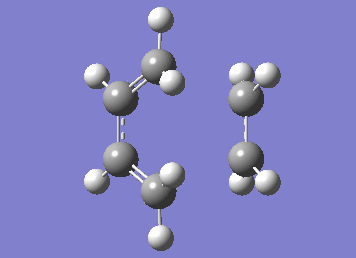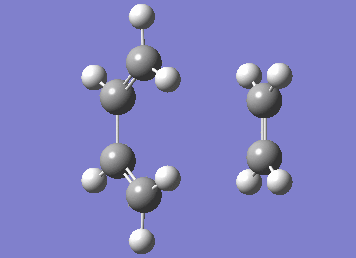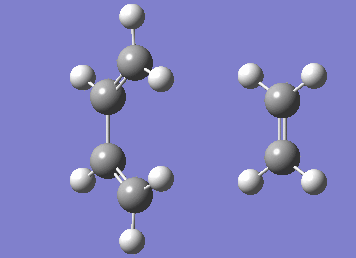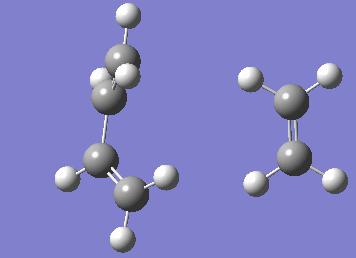
Reaction of Cyclohexa-1,3-diene and Maleic Anhydride

For this section, the starting materials, transition structures and final products have been optimised using AM1, HF/3-21G and B3LYP/6-31G*. The first of which is used to generate molecular orbitals and the second and third method used to analyse energy and geometry, with the latter of the two being more trustworthy (also more computationally expensive). (It is fine to use any of the methods, but it makes no sense to use the orbitals of one and the energies and geometries of another! João (talk) 21:05, 22 December 2014 (UTC))

Using semi-empirical AM1 method, the starting materials are optimised to minima and the frontier orbitals are presented. For cyclohexa-1,3-diene, its HOMO is antisymmetric with respect to the mirror plane separating the left and right part of the molecule, and its LUMO is symmetric with the same defined plane. For maleic anhydride, the symmetry is reversed. In contrast to the prototypical Diels Alder reaction above, both combinations of reactants' HOMO/LUMO pair allow largely constructive overlap to give both the exo and endo product.

IRC

For this situation, MO theory dictates the HOMO/LUMO pair with closer energy will interact more and contribute more to the transition state MO. It turns out this corresponds to the HOMO of the diene with the LUMO of anhydride. The estimated energy difference here is roughly 50% lower than the energy difference with the other HOMO/LUMO pair using AM1 (B3LYP/6-31G* also predicts similar percentage).

To determine the transition structures, the endo and exo final products were first drawn and optimised using AM1, following which the QTS2 method was used to try to link up the reactants (which were manipulated to orient in the seemingly correct ways) and product. Though this resulted in a run-time error.

The working method involves providing a guessed transition structure which then undergoes opt+freq optimisation to TS(Berny), calculating the force once. Only one negative frequency is obtained for both TS. The frequency value differ with different method, with AM1 giving the largest negative frequency (about 800 cm^-1) and B3LYP/6-31G* the smallest (a factor of 2 smaller than AM1). This trend is consistent for both TS which gives assurance that the calculations have been performed correctly, The animation below shows the vibration corresponding to the cycloaddition reaction.

Numerous attempts to produce the product by running IRC has failed to converge and resulted in errors before the the algorithm takES the second step. It has not been resolved even with demonstrator's help. Although running the IRC in the forward direction results in convergence and the desired starting materials are obtained.

Reactants Frontier Orbitals
	Cyclohexa-1,3-diene	Maleic Anhydride
HOMO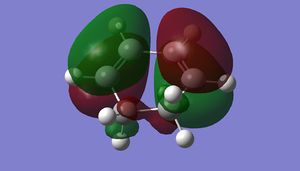
LUMO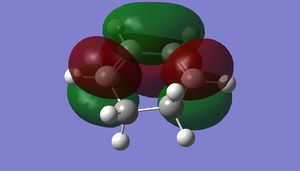

As both the exo and endo reactions involve the same type of primary orbital interaction, the four carbons (two on anhydride and two on the diene) hosting the newly formed σ bonds need to be within similar relative distances away from each other in both TS. (Using all three methods, this intermolecular distance for the exo and end TS only differ by at most 1 pm.) As a result of this, the sp² CH-CH fragment on the diene is in close vicinity with the -(C=O)-O-(C=O)- on the anhydride in the endo structure. While in the exo TS, it is the sp³ CH₂-CH² fragment on the diene that interacts with the -(C=O)-O-(C=O)- on the anhydride. In the latter case, the two hydrogens on the sp³ carbons will be closer to the maleic anhydride than in the endo case (hydrogens on the sp² carbons). B3LYP/6-31G* method shows hydrogens are closer by half an Angstrom in the exo and this leads to a more strained system, thus increasing the energy of the exo transition structure.

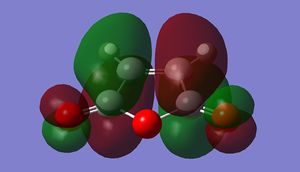
NBO Orbital Interactions

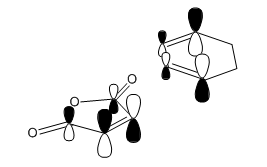
On top of the sterics, theory also predicts that the endo TS should have a lower energy than exo TS on orbital grounds. This is illustrated in the figure where a NBO picture of the relevant orbitals are drawn. The sizes of the orbital are not proportional to the amount of electron density. The larger set of orbitals corresponds to the primary, bond-forming overlap between the HOMO of the diene onto the LUMO of the anhydride. While the smaller set of orbitals depicts the constructive secondary orbital interactions between the HOMO of the diene with the anti-bonding orbitals on the carbonyl carbons that act to stabilise the system. This effect is not existent for the exo structure because the sp³ carbons do not have orbitals of the right symmetry to interact (the HOMO of cyclohexadiene shown hardly has any electron density on these two carbons) with the carbonyls .

Endo & Exo TS Reactive Vibrations
Exo Transition State	Endo Transition State

Using AM1, the MO of the occupied orbitals (only occupied orbitals contributes to electronic energy) are calculated to confirm whether this secondary orbital interaction effect can be observed. Starting with the HOMO, one can see significant electron density lies between and within the two molecules in the endo TS. Whereas about half of this major lopes lie outside of the molecules in the exo case. Though the author would classify this as the secondary orbital interaction with great reluctance. On the other hand, the HOMO-1 orbitals seems somewhat more promising as the carbonyl oxygens demonstrate orbitals that are in phase (red) with the lopes on the sp² carbons on the diene for the endo TS. This could potentially be the source of the secondary orbital interaction because in the exo TS there is no electron density on the sp³ carbons on the diene that can interact with the carbonyl oxygens.

MO Secondary Orbital Interactions
	Endo TS	Exo TS
Homo
HOMO-1

The following two tables present the electronic energies of the reactants, the two TS and the two products calculated using HF/3-21G as well as B3LYP/6-31G*. (AM1 gives spurious energy calculations. For instance, the anti 2 structure in the Cope rearrangement section gives 0.002380 a.u., which wildly differ from the readings obtain using HF or DFT but also a positive electronic energy for a ground state molecule does not make much physical sense) (It makes no sense to compare absolute energies, specially of different methods. You would find that the relative energies at AM1 would be reasonable. João (talk) 21:05, 22 December 2014 (UTC)). Before reading the values in the table, a quick sanity check on the relative magnitudes of the figures is done. Firstly, the transition structures are the highest point on the PES with respect to the reaction pathway so they should have larger energy values compared to the product, and also the sum of reactants' energies. Secondly, the combined effect of sterics and secondary orbital interaction depicted above means the the exo TS is higher in energy than the endo TS. Lastly, experiments have shown that the exo form is the thermodynamic product, meaning the exo product should be lower in energy than the endo product.

Energies Summary (hartree)
	Clcohexa-1,3-diene electronic energy	Maleic Anhydride electronic energy	Sum of reactants' electronic energies	Endo TS electronic energy	Exo TS electronic energy	Endo product electronic energy	Exo product electronic energy
HF/3-21G	-230.543231	-375.103513	-605.646744	-605.610368	-605.603591	-605.721320	-605.718735
B3LYP/6-31G*	-233.418916	-379.289535	-612.708451	-612.683395	-612.679335	-612.758310	-612.755778

The table above shows this reaction resides in a much deeper potential well than the Cope system investigated before. Again, energies calculated using B3LYP/6-31G* are always lower than the ones obtained using HF/3-21G, satisfying the variational principle as the former method incorporates a larger basis set and considers electronic correlation.

The activation energies is deduced using the data above.

Activation Energy (kcal/mol)
	HF/3-21G	B3LYP/6-31G*
ΔE (Endo)	22.826267	15.722865
ΔE (Exo)	27.078895	18.270552

An experimental value of 11.4 kcal/mol was obtained in a study of the kinetics of Diels Alder reaction under very high pressure (2000 atm), indicating the calculated values using B3LYP/6-31G* is in the correct region. Though the overestimation suggests a even larger basis set could be tried. Additionally, it has to be noted that although B3LYP/6-31G* does produce a closer activation energy to experimental value, it also predicts the exo product is less stable than the endo product. This is incorrect as the exo product is the thermodynamic product. HF/3-21G, on the other hand does give the correct ordering of product energy. The implications of this observation has not been further studied due to time constraint.

Further Discussion

As stated in the introduction section, reactions are studied computationally with neglect of any solvent effect and any secondary intermolecular effect with molecules not involved in the reaction. This is to reduce the computational complexity. Although no charged or radical intermediates exists during cycloaddition and therefore the Diels Alder reaction itself does not depend greatly on solvent system, solvent can still have an effect. For instance, in the particular case involving maleic anhydride, a polar solvent like dichloromethane (this is the solvent used in the aforementioned high pressure experiment) could stabilise the polar carbonyl groups, lowering the π* orbital energy therefore allowing better secondary orbital overlap. This could contribute to why the experimental activation energy is lower than computationally predicted. Additionally, it has been discovered that water has drastic accelerating effect on Diels Alder reactions, suggesting that solvent can be actively involved in shaping the reaction pathway and in turn the transition structure.

The second overlooked factor is perhaps the side-reaction for the diene to undergo cycloaddtion with another diene. An attempt is made to calculate the transition structure of the diene dimerisation process for both butadiene and cyclohexa-1,3-diene using B3LYP/6-31G*. In both cases, a structure with only one negative frequency is determined and is shown below, both demonstrating the dimerisation procedure.

Dimerisation

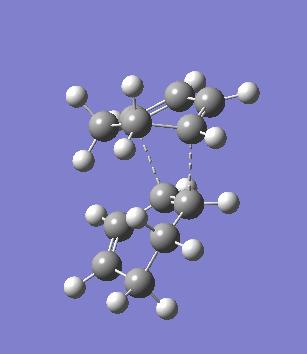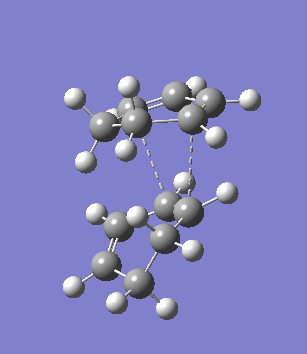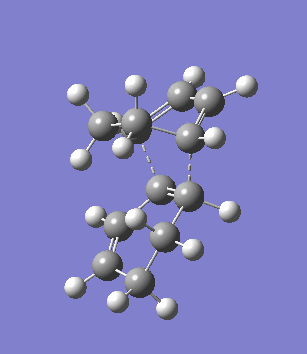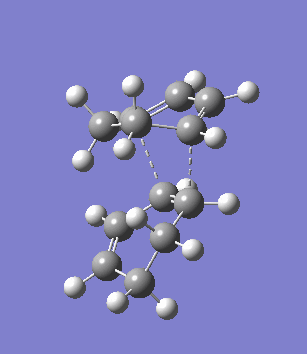
Frequency analysis of the cyclohexa-1,3-diene dimer TS is performed to obtain its energy and consequently the activation energy of the dimerisation reaction is calculated using additional data from the previous section. The calculated value of 30.737869 kcal/mol is about twice as high as the energy required to reach the endo product, indicating it should be a relative minor factor to consider. However, in a solvent system where the diene and dienophile do not intermix very well, then there is a high statistical preference for dimerisation and could greatly affect the product distribution.

Conclusions

In this exercise, sigmatropic rearrangement and cycloaddition has been investigated using quantum mechanical computation. A detailed study of the energies of Cope rearrangement conformers and transition structures has been carried out. The prototypical Diels Alder reaction and also the reaction between cyclohexa-1,3-diene and maleic anhydride has been conducted, the energies as well as the molecular orbitals analysed. It is found semi-empirical AM1 formalism provides the best orbital representation, whereas HF/3-21G and B3LYP/6-31G* are mostly used for energetic and geometry means. The latter performs better to give closer values when compared to experimental observations.

If more time was available, more expensive calculations can be performed (e.g. HF/6-31G*) and compared with experimental data. The wrong energy order produced by DFT calculation with regard to the exo and endo final products can be investigated using different basis sets too.