User:Sw1816

Ammonia Molecule

NH₃ optimising

Question	Answer
Molecular name	Ammonia
Calculation method	RB3LYP
Basis set	6-31G(d.p)
Final energy E(RB3LYP)/au	-56.55767490
RMS gradient norm/au	0.00199194
Point group	C_3v

ammonia molecule

N-H bond length=1.01798 Å
H-N-H bond angle=105.741 degrees

The literature value of the N-H bond is 1.01 Å, which matches the optimised ammonia molecule. However, the small uncertainty in the data shows that the structure optimised is not prefect. ^[1]

Charge distribution     N  -1.125     H  0.375 (From the optimisation)
Charge on the N is expected to be negative and the charge on H is expected to be positive, for the N is much more electronegative than H atom.

  Item                      Value     Threshold  Converged?
 Maximum Force            0.000004     0.000450     YES
 RMS     Force            0.000004     0.000300     YES
 Maximum Displacement     0.000072     0.001800     YES
 RMS     Displacement     0.000035     0.001200     YES
 Predicted change in Energy=-5.986284D-10
 Optimization completed.
    -- Stationary point found.

In the 'Item' table, the force value is very small and close to 0, which indicates the gradient of the energy potential to displacement graph is nearly zero. Therefore, the potential energy of the optimised ammonia structure is formed in the most stable structure at the lowest energy.

NH₃ molecule vibration

Questions

Mode	Frequency	Infrared
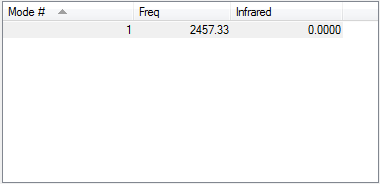
1	1089.54	145.3814
2	1693.95	13.5533
3	1693.95	13.5533
4	3461.29	1.0608
5	3589.82	0.2711
6	3589.82	0.2711

1. How many modes are expected?

Ammonia molecule has 4 atoms. Ammonia is expected to have 6 vibration modes according to 3N-6 modes.

2. Which modes are degenerate?

The vibration mode 2 and 3 are degenerate modes. The vibration mode 5 and 6 are degenerate modes.

3. Which modes are "bending" vibrations and which are "bond stretch" vibrations?

The mode 1, 2 and 3 are bending modes and the mode 4, 5 and 6 are stretching.

4. Which mode is highly symmetric?

The first mode is the most highly symmetric viration.

5. Which one is the "umbrella" mode?

The first vibration mode is the 'umbrella mode'.

6. How many bands are expected to see in an experimental spectrum of gaseous ammonia?

There are 2 peaks in the IR spectrum. The highest peak is at 1089.54 cm^-1 due to mode 1. The second peak is at 1693.95 cm^-1 due to mode 2 and 3. The peaks at 3461.29 and 3589.82 cm^-1 do not form a peak due to a low intensity. The mode 1 ,2 and 3 are stretching modes, so the change in dipole moment changes a lot due to change in distance between nitrogen and hydrogen atoms.

Nitrogen Molecule

N₂ molecule optimising

Question	Answer
Molecular name	Nitrogen
Calculation method	RB3LYP
Basis set	6-31G(d.p)
Final energy E(RB3LYP)/au	-109.52412868
RMS gradient norm/au	0.00000011
Point group	D_∞h

Nitrogen molecule

NΞN bond length = 1.10550 Å

The literature value of the NΞN bond is 1.10 Å, which matches the optimised ammonia molecule with small uncertainty.^[1]

Charge distribution  N 0.000    N 0.0000

Charge distribution of each atom in the molecule is 0.000, because there is no electronegativity difference between these two atoms.

   Item                     Value     Threshold  Converged?
 Maximum Force            0.000000     0.000450     YES
 RMS     Force            0.000000     0.000300     YES
 Maximum Displacement     0.000000     0.001800     YES
 RMS     Displacement     0.000000     0.001200     YES
 Predicted change in Energy=-1.029996D-14
 Optimization completed.
    -- Stationary point found.

In the 'Item' table, the force value is 0, which indicates the gradient of the energy potential to displacement graph is zero. Therefore, the potential energy of the optimised nitrogen structure is formed in the most stable structure at the lowest energy.

N₂ molecule vibration

Nitrogen molecule have no peak in IR spectrum. The nitrogen only has one frequency due to stretching of the N-N triple bond along the direction of the bond. Therefore, whatever the displacement are changed by the stretching, the changing diploe moment in the vibration of N₂ molecule is zero. Thus, the molecule would not absorb energy to vibrate.

Hydrogen Molecule

H₂ optimising

Question	Answer
Molecular name	Hydrogen
Calculation method	RB3LYP
Basis set	6-31G(d.p)
Final energy E(RB3LYP)/au	-1.17853936
RMS gradient norm/au	0.00002276
Point Group	D_∞h

Hydrogen molecule

H-H bond length= 0.74274 Å

The literature value of the H-H bond is 0.74 Å, which matches the optimised hydrogen molecule prefectly. Therefore, the hydrogen atom optimised is very close to the real structure of the hydrogen atom. ^[1]

Charge distribution    H  0.000     H  0.000

Charge distribution of each H atom in the molecule is expected to be 0.000, because these two H atoms have no electronegativity difference between each other.

 Item                      Value     Threshold  Converged?
 Maximum Force            0.000039     0.000450     YES
 RMS     Force            0.000039     0.000300     YES
 Maximum Displacement     0.000052     0.001800     YES
 RMS     Displacement     0.000073     0.001200     YES
 Predicted change in Energy=-2.043043D-09
 Optimization completed.
    -- Stationary point found.

In the 'Item' table, the force value is 0, which indicates the gradient of the energy potential to displacement graph is zero. Therefore, the potential energy of the optimised hydrogen molecular structure is formed in the most stable structure at the lowest energy.

H₂ molecule vibration

H₂ molecule has a higher frequency than the N₂ molecule. The vibrational frequency is related to force constant and reduced mass. The H₂ molecule is lighter than N₂ molecule, so the H₂ molecule has a higher frequency than nitrogen molecule.

Haber Process

Reaction energy

E(Ammonia)=-56.55767490 Hartrees = -148492.1867615 kJ/mol

2*E(Ammonia)=-113.1153498 Hartrees = -296984.373523 kJ/mol

E(Nitrogen)=-109.52412868 Hartrees = -287555.62175417 kJ/mol

E(Hydrogen)=-1.17853936 Hartrees = -3094.25532539 kJ/mol

3*E(Hydrogen)=-3.53561808 Hartrees = -9282.76597616 kJ/mol

ΔE=2*E(Ammonia)-[E(Nitrogen)+3*E(Hydrogen)]= -0.05560304 Hartrees = -145.99 kJ/mol (to 2 d.p)

ΔE(Ammonia)=0.5*ΔE= -72.50 kJ/mol (to 2 d.p)

The reaction energy is negative, so the energy of the ammonia product is lower than the gaseous reactants. The reaction is an exothermic reaction Therefore, the ammonia product is more stable than the nitrogen and hydrogen molecules.

The literature value of the Haber process is -45.8 kJ/mol.^[2] The energy of reaction calculated above does not match , but similar to the literature value. This may caused by the optimised structure. The optimised structure is not the real structure and has some uncertainty. Therefore, the calculation does not match perfectly.

Chlorine Trifluoride Molecule

ClF₃ optimising

Question	Answer
Molecular name	Chlorine trifluoride
Calculation method	RB3LYP
Basis set	6-31G(d,p)
E(RB3LYP)/au	-759.46531673
RMS Gradient Norm	0.00006708
Point group	C_2v

Chlorine trifluoride molecule

Chlorine trifluoride is a T-shaped molecule. Two F atoms are at axial position forming longer bonds with Cl atom. One F atom is at equatorial position with a shorter bond to Cl atom.

Cl-F bond length   1.65113 Å (one shorter bone), 1.72888 Å (two longer bonds)
F-Cl-F bond angle  87.119 degrees(two smaller angles), 174.238(one larger angle)

Charge distribution       Cl +1.225        F  -0.454(two F atoms), -0.316(one F atom)

The charge distribution og the chlorine is expected to be positive, because the electronegativity of the F atom is higher than Cl atom. In the molecule, each F atom have different distances to the Cl atom. Thus, the F atom with a shorter distance to Cl atom shows less negative.

 Item                       Value     Threshold  Converged?
 Maximum Force            0.000139     0.000450     YES
 RMS     Force            0.000091     0.000300     YES
 Maximum Displacement     0.000845     0.001800     YES
 RMS     Displacement     0.000552     0.001200     YES
 Predicted change in Energy=-1.619042D-07
 Optimization completed.
    -- Stationary point found.

In the 'Item' table, the force value is close to 0, which indicates the gradient of the energy potential to displacement graph is nearly negligible. Therefore, the potential energy of the optimised ClF₃ structure is formed in the most stable structure at the lowest energy.

ClF₃ molecule vibration

The frequencies of the ClF₃ molecule are low, because the Cl and F atoms are very heavy.

The peak with highest intensity is at 751.75 cm^-1. The peak is due to vibration of atoms in a long distance. When the Cl atom vibrates much, the changing dipole moment in the vibration is large. Therefore the mode 6 shows the highest intensity.

ClF₃ molecular orbital

The orbital 9 with energy of -1.28172 au (-3365.15612 kJ/mol) shows 3 σ bond. Each of the σ bonds is formed by the overlap of the 3s orbital in Cl atom and the 2s orbital orbitals in F atom. The overlap of the 2s-3s orbitals in phase forms the bonding.

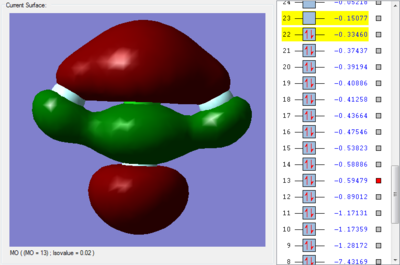
The orbital 13 with energy of -0.59479 au (-1561.62126 kJ/mol) shows 2 π bond and 1 σ bond. The F atom in axial position form π bond with the Cl atom by overlaping of the 2p orbital in F atom and the 3p orbital in Cl atom. The overlap of the 2p-3p orbitals in phase forms the π bonding. The F atom in equatorial position form σ bond with the Cl atom by overlaping of the 2p orbital in F atom and the 3p orbital in Cl atom. The overlap of the 2p-3p orbitals in phase forms the σ bonding.

The orbital 15 with energy of -0.53823 au (-1413.12297 kJ/mol) shows 3 π bond. Each of the F atom form π bond with the Cl atom by overlaping of the 2p orbital in F atom and the 3p orbital in Cl atom. The overlap of the 2p-3p orbitals in phase forms the π bonding.

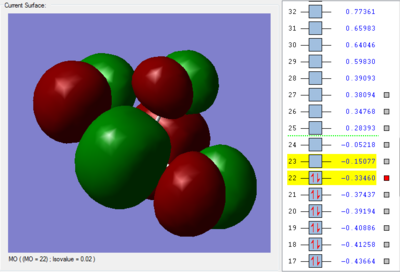
The orbital 22 with energy of -0.33460 au (-878.492367 kJ/mol) shows 3 π* bond. Each of the F atom form π* bond with the Cl atom by overlaping of the 2p orbital in F atom and the 3p orbital in Cl atom. The overlap of the 2p-3p orbitals out of phase forms the π anti-bonding.

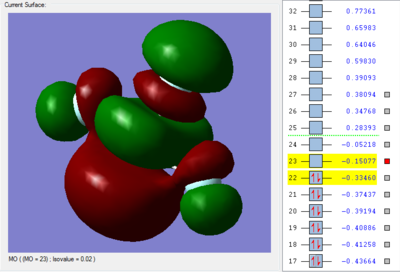
The orbital 23 with energy of -0.15077 au (-395.846665 kJ/mol) shows 2 π* bond and 1 σ* bond. The F atom in axial position form π* bond with the Cl atom by overlaping of the 2p orbital in F atom and the 3p orbital in Cl atom. The overlap of the 2p-3p orbitals out of phase forms the π anti-bonding. The F atom in equatorial position form σ* bond with the Cl atom by overlaping of the 2p orbital in F atom and the 3p orbital in Cl atom. The overlap of the 2p-3p orbitals out of phase forms the σ anti-bonding.

Extra calculation

Data used

Question	Answer
Molecular name	Hydrogen
Calculation method	RB3LYP
Basis set	6-31G(d.p)
Final energy E(RB3LYP)/au	-1.17853936
RMS gradient norm/au	0.00002276
Point Group	D_∞h

Question	Answer
Molecular name	Chlorine
Calculation method	RB3LYP
Basis set	6-31G(d.p)
Final energy E(RB3LYP)/au	-920.34987886
RMS gradient norm/au	0.00001378
Point Group	D_∞h

Question	Answer
Molecular name	Hydrogen chloride
Calculation method	RB3LYP
Basis set	6-31G(d.p)
Final energy E(RB3LYP)/au	-460.80077864
RMS gradient norm/au	0.00015892
Point Group	C_∞V

H-Cl bond length= 1.28658 Å

Cl-Cl bond length= 2.04168 Å

H-H bond length= 0.74274 Å

Calculation and analysis

The calculation below aims to gain the reaction energy of the reaction between chlorine and hydrogen. the chlorine and hydrogen could react with UV light to undergo a free-radical reaction.

E(Chlorine)=-920.34987886 Hartrees 

E(Hydrogen)=-1.17853936 Hartrees 

E(HCl)=-460.80077864 Hartrees

ΔEr=2*E(HCl)-[E(Chlorine)+E(Hydrogen)]= -0.07313898 Hartrees 

ΔE=0.5*ΔEr= -0.03656949 Hartrees = -96.01 kJ/mol (to 2 d.p)

The reaction is an exothermic reaction as the energy of the HCl is Lower than the gaseous reactants. Therefore, the product is more stable. The literature value of the reaction is -93.2 kJ/mol.^[3] The optimised data is pretty close to the literature value.

Reference

[Bond-1] 1.0 ^1.1 ^1.2 http://www.science.uwaterloo.ca/~cchieh/cact/c120/bondel.html

[Haber-2] ttps://en.wikipedia.org/wiki/Haber_process

[HCl_reaction-3] ttp://chemistry-reference.com/reaction.asp?rxnnum=317

[1]

[2]

[3]

Ammonia Molecule

NH3 optimising

NH3 molecule vibration