User:St908(module3)

The module2 is moved to module2

Tutorial

Optimizing the Reactants and Products

Results of Optimisation

	Anti conformation				gauche conformation
	Anti 1	Anti 2	Anti 3	Gauche 1	Gauche 2	Gauche 3
Energy(Hatree)	-231.692535	-231.690971	-231.689071	-231.692661	-231.691530	-231.687716
Symmetry	Ci	C1	C2h	C1	C2	C2

Anti 1 Ci conformation is optimised using more precise method,DFT with basis set 6-31G*. The energy of this optimised structure is -234.61171 Hatree which is 3 about hartree higher than the energy(-231.692535) obtained with HF/3-21G. These two structure has nearly no difference but the dihedral angles slightly differs with each other. (Note: The dihedral angle of centre four atoms calculated from 6-31G is exactly 180° which shows strict anti-conformation compared to a small deviation of dihedral angle obtained from 3-21G)

Thermodynamic

Procedure: The optimised Ci anti2 conformation of 1,5-hexadiene is confirmed by frequency analysis. Its thermodynamic properties is extracted from the log file.

Thermodynamic properties

Sum of electronic and zero point energies(0K)	-234.4692 Hatree
Sum of electronic and thermal energies(298.15K and 1atm)	-234.4619 Hatree
Sum of electronic and thermal enthalpies(298.15K and 1atm)	-234.4609 Hatree
Sum of electronic and thermal Free energies(298.15K and 1atm)	-234.5008 Hatree

Transition State Optimisation

Chair transition state

Chair TS by one step calculation

Chair TS by ONE step calculation

Chair TS by two steps calculation

Chair TS by TWO steps calculation

Comparison of structures of chair TS

Method use	(b)one step Method	(c)(d)Two steps Method
Bond length between terminal C-C(Å)	2.0199	2.0206
Energy(Hatree)	-231.61932231	-231.61932247
Imaginary Frequency(cm-1)	-817.854	-817.926

The Transition states of cope rearrangement reaction calculated using two methods are very similar in structures, energy and vibrational frequency. For the one step calculation method, as the accuracy of prediction can be enhanced by drawing the structure of transition state closer to ideal structure, the calculated result becomes less reliable if the structure transition state is not well defined. The two steps method has similar limitation but its calculation is simple as optimisation of the conformation of two allyl fragments are not involved in the optimisation of the transient bonds between two fragments. The results produced illustrates that the two steps method performs a good approximation compared to one step method. It can be introduced to optimise larger molecule which would consume more ICT system resources.

Boat transition state

Boat QTS2 calculation

Boat transition structure by QTS2 calculation

IRC calculation: Find the conformation relaxing from transition state with lowest energy path.(forward reaction here)

The transition structure can be predicted by providing guessed reactant and product using QTS2 calculating methods. However, the product may not be the most favourable product forming from predicted transition state. The IRC method can predict the favourable product in either direction. The transition structure was performed IRC calculation with N(number of reaction coordinates) equals to 50. The resultant energy did not reach minimum since the IRC gradient did not converge to zero. Since the gradient for the last structure was very close to zero(gradient=0.00087), it got optimised using DFT/BL3YP with basis set 6-31G*. I also repeated the calculation but this time the N point was set to 70. The IRC results showed that minimum energy was achieved at the 69th structure.

IRC results comparison

	50th structure followed by optimisation irc50	69th structure Boat QTS2 calculation
Energy(Hatree)	-234.611329	-234.611177
Gradient	0.0000077	0.0001

Using two methods shown above, the two product has similar structure resembling the Gauche3/C1 structure which is also the lowest energy conformation in Appendix2. As two predictions are similar, the first method, optimisation of the last structure provides precision rather than accuracy as the gradient is 0.0000077, much more precise than 0.0001. The most favourable conformation can be only obtained in ideal condition(ie. zero point energy) as interconversion of different conformations occurs in experimental condition(ie. high temperature)

Activation Energy

Using higher level calculation method, dft/b3lyp with basis set 6-31G*, the transition structure and its related reactant got further optimised. This process can enhance the accuracy of predicting the activation energy. The strategy of choosing reactant for comparison is to choose the one resembles the transtion state. The energy differences between the reactants with different conformations are less than 3kcal/mol that will not affect the results strongly. The activation energy required for interconversion between different conformation is around 4-6kcal/mol At elevated temperature where the Cope rearrangement reaction can proceed, all the conformations will convert to the conformation close to the transition states(boat or chair).

Energy of reactants and product Summary (All the data below is based on B3LYP/6-31G*)

	Reactants		Transition states
	Anti2(Ci)	Gauche3 (C1)	Chair	Boat
Energy(T=0K, zero-point energy, Hartree)	-234.469204	-234.468693	-234.414929	-234.402341
Energy(T=298.15K, Hartree)	-234.461857	-234.461464	-234.409008	-234.396007

The energy difference between conformation of two reactant(3kcal/mol) is smaller compared with difference between two transition states(8kcal/mol)

Activation energy estimation

	Anti2(reactant) → Chair(TS)	Gauche3(reactant) → Boat(TS)
Activation energy(0K, kcal/mol)	34.05(4s.f)	41.63(4s.f)
Activation energy(298.15K, kcal/mol)	33.17(4s.f)	41.08(4s.f)
Experimental activation energy at 0K(kcal/mol)	33.5±0.5	44.7±2.0

For activation energy via chair transition structure at 0K, the calculated value is 0.05kcal/mol higher than the experimental results including error which the prediction is acceptable. For boat transition structure, the calculated results is 1.07kcal/mol lower than the experimental value including error. This deviation from experimental is caused by the limitation of methods and basis set used for molecular modelling. The activation energy via both transition states at room temperature and pressure are lower than that at zero point energy. We can deduce that the energy increase of the transition state is less than the energy increase of the corresponding reactant.

Diels Alder Reaction

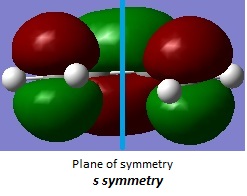
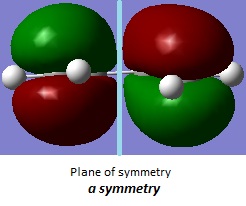
Butadiene HOMO and LUMO symmetry

Butadiene

Optimised Cis-Butadiene structure

LUMO	HOMO

Examine the transition state

The transient double bond is used to plot the butadiene fragment for gaussian input file as all three bonds are involved in the reaction. Therefore the bond length of transient double bond is close to the length of bond being formed and broken during transition state. The distance between the terminal carbon of two reactants is adjust approximately to 2Å. The optimised transition structure shows the distance of bond being formed is about 2.12Å. The imaginary vibrational frequency is observed at -806cm^-1 tells us the reaction is concerted formation as the vibration is symmetrical.

Diels alder TS

Optimised Transition structure

Bond length in TS

	Butadiene		Ethene
	sp2-sp2 C-C single bond	sp2-sp2 C=C double bond	sp2-sp2 C=C double bond
Calculated bond length in TS(Å)	1.40	1.38	1.38
Normal bond length(Å)	1.47	1.34	1.34
New σ bond formed in transition state(Å)	2.12

C-C single bond in TS is longer than literature while C=C double bond is shorter than literature. In transition state, all the bonds involved in the reaction are transient bond whose nature is a mixture of double and single bond. The new σ bond formed in transition state is 2.12Å which is much longer than the covalent C-C bond length.

Diels alder(maleic anhydride and cyclohexa-1,3-diene

Using optimisation of TS(berny) with semiempirical AM1 methods, the transition state of diels alder reaction bewteen maleic anhyride and cylcohexa-1,3-diene is calculated with MO information. As this reaction is normally governed by kinetic aspects, endo and exo transition state are calculated for analysis.

transition structure and their Orbitals

	HOMO	LUMO
Maleic anhydride
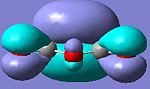
Cyclohaxa-1,3-diene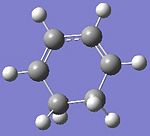
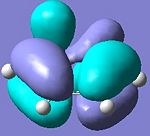
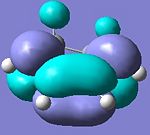
endo TS
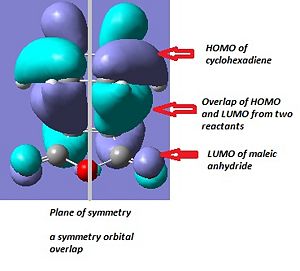
exo TS

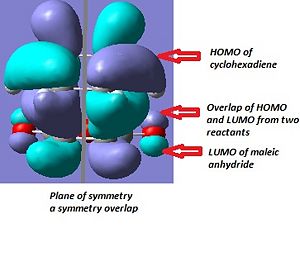
From the illustration in the table above, we can conclude the HOMO of cyclohexadiene overlap with LUMO of maleic anhydride for both endo and exo transition state. This is consistent with the face that oxygen atom is electronegative and lower the energy of maleic anhydrous compared to ethene. Therefore the cyclohexadiene is acting as electron donor.

Energy Summary of TS

	endo	exo
electronic energy(Hartree)	-0.051594	-0.050503
Bond length between transition state C-C interaction	2.16Å	2.17Å

Normal sp³ C-C bond length and sp² C=C bond length are about 1.54Å and 1.34Å respectively. The C-C bonds in cyclohexadiene that involved in the reaction in transtion state are around 1.39Å for both endo and exo TS while the C-C bond in maleic anhydride is about 1.41Å. These bond length are in the middle of length of single and double bond. The C-C new bond being formed in TS are 2.16Å and 2.17Ά which are much larger than the covalent C-C bond length. If we compare the electronic energy between endo and exo TS, endo TS is about 0.68kcal/mol more stable than exo TS. If we only consider that the exo TS conformation has less steric effect than endo TS, then exo have to be stablet than endo conformation. However, the secondary orbital overlap is a stronger influence than steric reason.

Secondary orbital overlap

	endo	exo
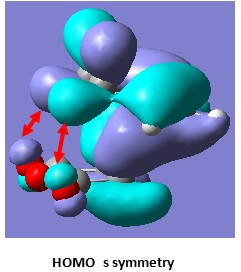
Interaction distance(endo:-C=O and -CH=CH- distance through space, exo:-CH2-CH2- and -C=O)	2.89Å	2.94Å

We can see that all the C=O π or π* orbital has same symmetry as its face to face orbital through space. This interaction distance is about 0.8Å longer than primary interaction in transition state(2.16-2.17Å). Therefore the secondary overlap is much weaker than the primary overlap. If we compare the overlap between endo and exo, the interaction distance indicate the exo has weaker overlap due to longer distance. In addition, both HOMO and HOMO-1 in endo transition state have overlap with same symmetry. The exo transition sate only has interaction between σC-H and πC=O in its HOMO.

For exo TS, the immaginary frequency is observed at -811.53cm^-1 while 6 immaginary modes from -38 to-989cm^-1 are observed in endo TS. This attribute to plenty of orbital interactions other than the interaction used for forming new bond in diels alder reaction. The immaginary vibration in exo shows concerted bond formation.