User:Sam11
The Cope Rearrangement Tutorial
Optimizing the Reactants and Products
1a-d. Hexa-1,5-diene was drawn using the cyclohexane fragment from the GaussView 05 Builder tool, selecting two bonds at the 1 and 5 positions, changing these to double bonds and deleting the bond between them. Carbon valency was checked and the structure cleaned with the cleaning tool. The C3-C4 single bond was used as a central axis around which the R groups were rotated, positioning these at 90 degrees to each other (antiperiplanar) with all bonds staggered around the central C3-C4 axis. This structure was optimised to a minimum at HF 3-21G level of theory. The orientation of the terminal groups resulted in higher than expected for the antiperiplanar arrangement. With reference to Appendix I, and literature reports,[1] these groups were rotated around the C2-C3 and C4-C5 bonds respectively, and optimised to HF 3-21G level of theory.
Conformations in order of increasing energy are arranged below.
Total Energy = -231.68771613 a.u. RMS Gradient Norm = 0.00001361 a.u. Dipole Moment = 0.4556 Debye
Total Energy = -231.68907066 a.u. RMS Gradient Norm = 0.00000551 a.u. Dipole Moment = 0.0001 Debye
Total Energy = -231.68916017 a.u. RMS Gradient Norm = 0.00001050 a.u. Dipole Moment = 0.5360 Debye Point Group = C2
Total Energy = -231.68961574 a.u. RMS Gradient Norm = 0.00001037 a.u. Dipole Moment = 0.4439 Debye
Total Energy = -231.69097056 a.u. RMS Gradient Norm = 0.00000667 a.u. Dipole Moment = 0.2954 Debye Point group = Ci
Total Energy = -231.69153032 a.u. RMS Gradient Norm = 0.00001866 a.u. Dipole Moment = 0.1281 Debye Bond lengths (A): C1-C2 = 1.35520 C2-C3 = 1.54000 C3-C4 = 1.54000 C4-C5 = 1.54000 C5-C6 = 1.35520
Total Energy = -231.69253530 a.u. RMS Gradient Norm = 0.00000381 a.u. Dipole Moment = 0.0000 Debye Point group = Ci
Total Energy = -231.69266122 a.u. RMS Gradient Norm = 0.00000126 a.u. Dipole Moment = 0.3406 Debye Point group = C1
b. To achieve the gauche structure, the C3-C4 bond was used as a central axis. Around this the terminal R groups were rotated to give a staggered conformation, with the two alkyl R groups positioned at 60 degrees to each other. Again, the energy was higher than expected due to the steric clashing of the terminal alkene groups. These were rotated around the C2-C3 and C4-C5 bonds to reduce this effect. In agreement with Appendix I, the gauche3 geometry was obtained as the lowest energy conformer of 1,5-hexadiene.
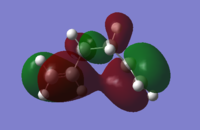
The gauche6 energy is 0.00181034 a.u (1.136 kcal/mol)higher in energy, and less stable, than the anti-periplanar2 conformer. This is as expected from literature, which documents roughly ~0.7 kcal/mol increase in energy moving from anti-periplanar to gauche geometry in butane due to reduction in steric clashing between terminal hydrogens, which exhibit repulsive VdW interactions. Gauche3 energy is lower and more stabilised than antiperiplanar2 due to the reduced distance between the two allylic groups in the gauche3 conformer. This does not result in steric clashing, nor favourable VdW cloud overlap, of terminal hydrogens, as they are too far apart(with the smallest inter-hydrogen separations at 3.39354, 3.80768, 5.09754 and 5.40562 A, all distances outwith the VdW overlap region of ~2.5 A). The reduced distance between the terminal allylic groups allows favourable in-phase overlap of the two pi clouds, which cannot occur in the anti2 conformer as the two groups are pointing towards opposite ends of the molecule. This interaction is present in the HOMO of gauche3, and is shown below.
HOMO gauche3:
HOMO anti2:
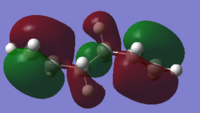
The favourable pi-pi interaction results in the gauche3 conformer lying at the lowest energy of all 10 possible conformers.
1.d. Anti2 hexa-1,5-diene was constrained to Ci symmetry and energy at HF 3-21G level optimised. Energy = -231.69253515 a.u
Anti2 hexa-1,5-diene at HF 3-21G level of theory, constrained to Ci symmetry
As this energy was higher than symmetrised Ci output conformer of the first HF 3-21G optimisation, this geometry was not used for following calculations.
Geometry of the -231.6925353 a.u Ci symmetrised anti2 conformer:
| Bond | Bond Length (A) | Bond Angle | Angle (degrees) |
| C1-C2 | 1.31615 | C1-C2-C3 | 124.81552 |
| C2-C3 | 1.50884 | C2-C3-C4 | 111.34916 |
| C3-C4 | 1.55286 | C3-C4-C5 | 111.34916 |
| C4-C5 | 1.50884 | C4-C5-C6 | 124.81552 |
| C5-C6 | 1.31615 | ||
f. Both the anti2 and the gauche3 geometries were optimised to DFT B3LYP 6-31G* level of theory.
Gauche3 Results:
gauche3 optimised at DFT B3LYP 6-31G* level of theory
Total Energy = -234.61132934 a.u. RMS Gradient Norm = 0.00000174 a.u. Dipole Moment = 0.3960 Debye Point Group = C1
Geometry:
| Bond | Bond Length (A) | Bond angle | Angle (degrees) |
| C1-C2 | 1.3336 | C1-C2-C3 | 124.93368 |
| C2-C3 | 1.50438 | C2-C3-C4 | 113.46394 |
| C3-C4 | 1.55013 | C3-C4-C5 | 113.47739 |
| C4-C5 | 1.5049 | C4-C5-C6 | 125.47837 |
| C5-C6 | 1.33382 | ||
Anti2 Results: Anti2 hexa-1,5-diene was optimised to DFT B3LYP/6-31G* and symmetrised to Ci symmetry.
anti2 Ci symmetry at DFT B3LYP 6-31G* level of theory
Energy = E(RB3LYP) = -234.61170280 a.u. RMS Gradient Norm = 0.00000285 a.u. Dipole Moment = 0.0000 Debye
Geometry:
| Bond | Bond Length (A) | Bond Angle | Angle (degrees) |
| C1-C2 | 1.335 | C1-C2-C3 | 125.28548 |
| C2-C3 | 1.50423 | C2-C3-C4 | 112.6663 |
| C3-C4 | 1.54816 | C3-C4-C5 | 112.6663 |
| C4-C5 | 1.50423 | C4-C5-C6 | 125.28548 |
| C5-C6 | 1.335 | ||
Thus, as the level of theory is increased from HF to DFT B3LYP, the overall geometry does not change significantly, with 0.01885, -0.00461 and -0.0047 A increases in C1-C2, C2-C3 and C3-C4 bond lengths, and 0.46996 and 1.31714 degree increases in C1-C2-C3 and C2-C3-C4 angles.
Constraining the result of the first DFT B3LYP optimisation to Ci symmetry, the DFT optimisation was run again, giving a lower energy, and thus more stable, conformer which was thus used in following calculations.
Anti2 hexa-1,5-diene Ci symmetry at DFT B3LYP 6-31G* level of theory
Energy = -234.6117136 a.u RMS gradient norm = 0.00003714 a.u
Geometry:
| Bond | Bond Length (A) | Bond Angle | Angle (degrees) |
| C1-C2 | 1.35516 | C1-C2-C3 | 120.00659 |
| C2-C3 | 1.54001 | C2-C3-C4 | 109.58041 |
| C3-C4 | 1.53171 | C3-C4-C5 | 109.58041 |
| C4-C5 | 1.54001 | C4-C5-C6 | 120.00659 |
| C5-C6 | 1.35516 | ||
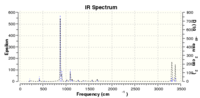
g. DFT B3LYP 63-1Gd* frequency calculation carried out for both the lower energy Ci conformer and the higher energy Ci conformer shown in part f above, solvent specified as "none", with IR spectrum and lowest wavelength vibration as attached.
Lower energy Ci anti2 gave an IR spectrum shifted to higher frequencies, with the lowest energy vibration at 74.98 cm-1.

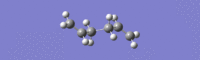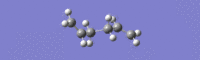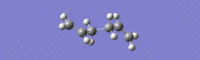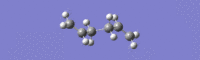
Higher energy Ci anti2 gave an IR spectrum shifted to lower frequencies, with the lowest energy vibration at 74.26 cm-1.


h. The thermochemistry data was accessed from the chk output file for both higher energy conformer and lower energy conformer, with results summarised below.
Higher energy Ci anti2 conformer:
| Energy Contribution | Energy (a.u/particle) | Energy (kcal/mol) |
| zero-point vibrational energy | 0.142507 | 89.4245117 |
| thermal energies | 0.149853 | 94.0341973 |
| thermal enthalpies | 0.150797 | 94.6265664 |
| thermal free energies | 0.110933 | 69.6115233 |
| electronic energy | ||
| electronic + zero-point | -234.469204 | |
| electronic + thermal energies | -234.461857 | |
| electronic + thermal enthalpies | -234.460913 | |
| electronic + thermal free energies | -234.500778 | |
| Energy Contribution | Energy (thermal) (kcal/mol) | CV ( cal/mol.Kelvin) | S (cal/mol.Kelvin) |
| Total | 94.034 | 25.46 | 83.902 |
| Electronic | 0.000 | 0.000 | 0.000 |
| Translational | 0.889 | 2.981 | 39.129 |
| Rotational | 0.889 | 2.981 | 26.823 |
| Vibrational | 92.257 | 19.498 | 17.949 |
Temperature was changed using Gaussian 09W, and carrying out a FreqChk on the chk output file of the Frequency calculation of the anti2 DFT B3LYP level conformer.
At 0.1 K, 1 atm:
| Energy Contribution | Energy (a.u/particle) | Energy (kcal/mol) |
| zero-point vibrational energy | 0.142507 | 89.4245117 |
| thermal correction to energies | 0.142508 | 89.42501372 |
| thermal correction to enthalpies | 0.142508 | 89.42501372 |
| thermal correction to free energies | 0.142507 | 89.3209726 |
| electronic energy |
As expected here, the zero-point vibrational energy does not change when temperature is reduced close to 0K, whilst the thermal correction to energies and enthalpies decrease. Thermal correction to free energies increases with temperature reduction.
| Energy Contribution | Energy (thermal) (kcal/mol) | CV ( cal/mol.Kelvin) | S (cal/mol.Kelvin) |
| Total | 89.425 | 5.962 | 2.361 |
| Electronic | 0.000 | 0.000 | 0.000 |
| Translational | 0.000 | 2.981 | -0.616 |
| Rotational | 0.000 | 2.981 | 2.976 |
| Vibrational | 89.424 | 0.000 | 0.000 |
It can be seen that at 298.15 K, vibrational energy contributes the majority of the thermal energy, with electronic energy contributing 0 kcal/mol. At low temperature, close to 0K, it can be seen that all degrees of freedom are reduced in energy. The distribution in thermal energy reduces in translational and rotational contributions to 0 kcal/mol, with the zero-point vibrational energy contributing to total thermal energy.
At 400 K, 1 atm:
| Energy Contribution | Energy (a.u/particle) | Energy (kcal/mol) |
| zero-point vibrational energy | 0.142506551 | 89.42423 |
| zero-point correction | 0.142506551 | 89.42423 |
| thermal correction to energies | 0.15464 | 94.0247846 |
| thermal corrrection to enthalpies | 0.155907 | 94.6171537 |
| thermal correction to free energies | 0.096564 | 69.5926981 |
| Energy Contribution | Energy (thermal) (kcal/mol) | CV ( cal/mol.Kelvin) | S (cal/mol.Kelvin) |
| Total | 97.038 | 33.491 | 93.095 |
| Electronic | 0.000 | 0.000 | 0.000 |
| Translational | 1.192 | 2.981 | 40.589 |
| Rotational | 1.192 | 2.981 | 27.699 |
| Vibrational | 94.654 | 27.529 | 24.807 |
Lower energy Ci anti2 conformer:
| Energy Contribution | Energy (a.u/particle) | Energy (kcal/mol) |
| zero-point vibrational energy | 0.142486 | 89.411334 |
| thermal correction to energies | 0.149838 | 94.0247846 |
| thermal corrrection to enthalpies | 0.150782 | 94.6171537 |
| thermal correction to free energies | 0.110903 | 69.5926981 |
| electronic energy | ||
| electronic + zero-point | -234.469226 | |
| electronic + thermal energies | -234.461874 | |
| electronic + thermal enthalpies | -234.46093 | |
| electronic + thermal free energies | -234.500808 | |
| Energy Contribution | Energy (thermal) (kcal/mol) | CV ( cal/mol.Kelvin) | S (cal/mol.Kelvin) |
| Total | 94.024 | 25.472 | 83.931 |
| Electronic | 0.000 | 0.000 | 0.000 |
| Translational | 0.889 | 2.981 | 39.129 |
| Rotational | 0.889 | 2.981 | 26.823 |
| Vibrational | 92.247 | 19.510 | 17.979 |
The chk file for the higher energy Ci anti2 conformer could not be accessed, even after repeating the DFT B3LYP optimisation. Changing the temperature therefore could not be carried out.
'Optimizing the "Chair" and "Boat" Transition Structures
Note: The convergence of transition state optimisations should be carried out with the transition state obtained from the previous optimisation with the lowest RMS gradient, as this represents the point on the PES which will be closest to the reaction pathway.
Note: The imaginary frequency represents the steepest descent down the PES. there is one imaginary frequency for a TS because it is a minimum in all other directions but it is the only maximum.
a. A conjugated propene fragment was drawn beginning with an allyl fragment. One hydrogen was changed to a carbon, both bonds were specified as conjugated, valences were corrected and structure was cleaned. Initial guess structure was approximated using the delocalised bond length and C1-C2-C3 bond angle of benzene: 1.39483 A and 119.99399 degrees. This returned the structure shown below:
1. Allyl fragment, input benzene CC bond lengths 1.39483 A, optimized to the HF 3-21g level of theory
E(UHF) = -115.82304003 a.u. RMS Gradient Norm = 0.00005396 a.u Dipole Moment = 0.0290 Debye Point Group = C2v
| Bond | Bond Length (A) | Bond Angle | Angle (degrees) |
| C1-C2 | 1.38847 | C1-C2-C3 | 124.26952 |
| C2-C3 | 1.38847 | ||
The bond lengths were reduced to 1.39 A each and the HF 3-21G optimisation repeated, results shown below:
2. Allyl fragment, input CC bond lengths 1.39 A, optimized to the HF 3-21g level of theory
Total Energy = -115.82304009 a.u. RMS Gradient Norm = 0.00001153 a.u Dipole Moment = 0.0292 Debye Point Group = C2v
| Bond | Bond Length (A) | Bond Angle | Angle (degrees) |
| C1-C2 | 1.38851 | C1-C2-C3 | 124.30100 |
| C2-C3 | 1.38851 | ||
A final trial was carried out, with input bond lengths of C1-C2 1.51 A, C2-C3 1.33 A manually specified, to comply with literature data,[2] and this structure optimised to the HF 3-21G level. Results are shown below.
3. Allyl fragment, input CC bond lengths 1.51 and 1.33 A, optimized to the HF 3-21g level of theory
E(UHF) = -115.82303999 a.u. RMS Gradient Norm = 0.00005750 a.u Dipole Moment = 0.0292 Debye Point Group = C2v
| Bond | Bond Length (A) | Bond Angle | Angle (degrees) |
| C1-C2 | 1.38836 | C1-C2-C3 | 124.29892 |
| C2-C3 | 1.38836 | ||
b. All three structures above were input into TS optimisations. TS results involving the optimised allyl fragments are documented below with the same numbering as above, respectively.
1. Allyl fragment no. 1 was copied twice into a new MolGroup and w.r.t Appendix II, the molecules were aligned in a cyclohexane chair-like TS structure, with an input terminal CC separation at 2.2 A. This was optimised at HF 3-21G level of theory, and results documented below.
no.1 allylic fragment TS optimised to HF 3-21G level of theory
E(RHF) = -231.61932243 a.u. RMS Gradient Norm = 0.00002281 a.u (good approximation) Dipole Moment = 0.0010 Debye Point Group = C2h
Geometry of the TS:
| Bond | Bond Length (A) | Bond Angle | Angle (degrees) |
| C1-C2 | 1.38961 | C1-C2-C3 | 120.4971 |
| C2-C3 | 1.38961 | ||
| terminal C1-C1 | 2.01958 | ||
| terminal C3-C3 | 2.01958 | ||
A frequency calculation was carried out at this level of theory. One imaginary frequency was found at -817.91 cm-1 (IR 5.8594), indicating the correct identification of a TS. Referring to the tutorial wiki, the agreement of this TS vibration with the 818 cm-1 expected frequency reinforces this.

2. In order to assess the validity of this TS before continuing with constraint optimisation calculations, another chair transition state structure was drawn, using the allylic fragment denoted as no. 2 above. Results are summarised below.
Total Energy = -231.61932222 a.u. RMS Gradient Norm = 0.00003371 a.u (not as good an approximation as no.1) Dipole Moment = 0.0009 Debye
Geometry:
| Bond | Bond Length (A) | Bond Angle | Angle (degrees) |
| C1-C2 | 1.39017 | C1-C2-C3 | 120.49426 |
| C2-C3 | 1.39017 | ||
| terminal C1-C1 | 2.01821 | ||
| terminal C3-C3 | 2.01821 | ||
A frequency calculation at the HF level gave one imaginary frequency at -817.96 cm-1 (IR 5.8778). This is shown below with an IR spectrum.

The no. 2 allyl fragment was reoriented and the optimisation rerun at HF level of theory. This was done as a precautionary measure as the no.2 allyl fragment had the lowest optimised energy, and the TS(berny) optimisation returned a higher energy than that of no.1, which was not expected. Results are below.
no.2 allylic fragment TS optimised to HF 3-21G level of theory
E(RHF) = -231.61932245 a.u. RMS Gradient Norm = 0.00001053 a.u (good approximation) Dipole Moment = 0.0004 Debye Point Group = C2h
Geometry:
| Bond | Bond Length (A) | Bond Angle | Angle (degrees) |
| C1-C2 | 1.38865 | C1-C2-C3 | 120.49408 |
| C2-C3 | 1.38865 | ||
| terminal C1-C1 | 2.0219 | ||
| terminal C3-C3 | 2.0219 | ||
Frequency calculation gave one imaginary frequency at -818.14 cm-1, which is shown below.

3. Using the allyl fragment no.3 from part a, the terminal carbons of the two allylic fragments were manually spaced at 2.2 A apart using the bond picking tool. This TS(berny) structure was optimised to the Hartree Fock 3-21G level of theory, returning a lower more stable TS energy of -231.61932246 a.u
no.3 allylic fragment TS optimised to HF 3-21G level of theory
E(RHF) = -231.61932246 a.u. RMS Gradient Norm = 0.00001082 a.u. (as this is close to zero (to 5 d.p), it can be deduced that the TS(berny) calculation converged to a minimum. Imaginary Freq = 1 Dipole Moment = 0.0001 Debye Point Group = C1
Final terminal CC bond lengths lie at 2.02031 and 2.02020 A
One TS(berny) imaginary frequency of -817.93 cm-1 was calculated, corresponding to the following vibration.
Following the different imaginary frequencies obtained from reorientation of the allylic fragments in no.2, the no.3 fragments were reoriented, with 2.2 A kept between terminal carbons as input. This gave results as follows:
improved no.3 allylic fragment TS optimised to HF 3-21G level of theory
Total Energy = -231.61932246 a.u. RMS Gradient Norm = 0.00001052 a.u. Imaginary Freq = Dipole Moment = 0.0001 Debye
Geometry:
| Bond | Bond Length (A) | Bond Angle | Angle (degrees) |
| C1-C2 | 1.38929 | C1-C2-C3 | 120.49856 |
| C2-C3 | 1.38929 | ||
| terminal C1-C1 | 2.0202 | ||
| terminal C3-C3 | 2.02031 | ||
Frequency calculation gave an imaginary frequency at -818 cm-1, which is shown below.

The imaginary vibration for all three TS are similar, and represent the reaction path down the steepest energy slope from TS to product. This appears to be a synchronous reaction mechanism, with the contraction of forming bonds and lengthening of breaking bonds occurring simultaneously. Upon inspection of the frequency of vibration, the TS optimised from the no.1 allylic fragment has the highest relative error with the expected frequency of 818 cm-1 than the TS optimised from the no.3 and no.2 allyl fragments. The improved no. 3 TS, with the lowest frequency relative error and lowest TS energy (HF) may provide the most accurate approximation. The no. 1 and no.2 allylic fragment TS have higher energies following optimisation, and thus do not represent the most favourable TS for the reaction pathway.
Thus the improved no.3 TS, with imaginary frequency of -818 cm-1, was optimised further to DFT B3LYP 6-31G* level of theory, results documented below, and the HF level of theory TS was used for any following calculations.
Results:
improved no.3 allylic fragment TS optimised to DFT B3LYP level of theory
E(RB3LYP) = -234.55698303 a.u. RMS Gradient Norm = 0.00001192 a.u. Imaginary Freq = 1 Dipole Moment = 0.0000 Debye Point Group = C2h
Geometry:
| Fragment Involved | Bond | Bond Length (A) | Bond Angle | Angle (degrees) |
| Fragment 1 | C1-C2 | 1.4075 | C1-C2-C3 | 119.95241 |
| C2-C3 | 1.4075 | |||
| Inter-fragment distances | terminal C1-C1 | 1.96755 | ||
| terminal C3-C3 | 1.96755 | |||
| Fragment 2 | C1-C2 | 1.4075 | C1-C2-C3 | 119.95241 |
| C2-C3 | 1.4075 | |||
Frequency calculation: One imaginary frequency at -565.54 (IR 0.0826)
The assignment of the synchronous mechanism agrees with literature, which documents the synchronous mechanism being favoured over asynchronous, as the resulting synchronous mechanism aromatic TS lies at a lower energy than the biradical TS resulting from the alternative asynchronous mechanism.[3] The TS of the synchronous mechanism is a barrier as it corresponds to an electronic rearrangement: a change of spin coupling with the changing from one Kekule structure to another.[3]
The results of such literature records were evaluated loosely in the present study, through modelling of the biradical TS reported and vibrational structure, at HF 3-21G level of theory. Summary of the key results are shown below.
biradical TS optimised to HF 3-21G level of theory
E(RHF) = -231.54077330 a.u. RMS Gradient Norm = 0.00005744 a.u. Imaginary Freq = 1 Dipole Moment = 0.4035 Debye Point Group = C1
Imaginary frequency:
The total energy is higher than the synchronous mechanism aromatic TS, as expected. The imaginary vibration shows explicitly the asynchronicity of the alternative mechanism.
c. In order to check the validity of this calculated TS, and possibly increase the accuracy of the optimisation a constraint-derivative optimisation method was applied.
Constraint and Optimisation to Minimum: Using the redundant coordinate tool, the two terminal CC bonds were selected, and bonds frozen at 2.2 A. An optimisation (minimum) was carried out for this structure, at the HF 3-21G level of theory, with opt=noeigen specified as an additional keyword. This optimised all bond lengths in this structure so that a minimum energy was reached, whilst freezing the inter-fragment distance.
improved no. 3 TS optimised to minimum at HF 3-21G level of theory
Results: Charge = 0 Spin = Singlet E(RHF) = -231.61518537 a.u. RMS Gradient Norm = 0.00325935 a.u. Imaginary Freq = 0 Dipole Moment = 0.0000 Debye Point Group = C1
Geometry:
| Fragment Involved | Bond | Bond Length (A) | Bond Angle | Angle (degrees) |
| Fragment 1 | C1-C2 | 1.38130 | C1-C2-C3 | 121.97358 |
| C2-C3 | 1.38130 | |||
| Inter-fragment distances | terminal C1-C1 | 2.2 | ||
| terminal C3-C3 | 2.2 | |||
| Fragment 2 | C1-C2 | 1.38130 | C1-C2-C3 | 121.97360 |
| C2-C3 | 1.38130 | |||
d. Derivative and Optimisation to (TS(berny):The resulting output .chk file for the optimised structure from part c was used in the following calculation. Using the redundant coordinate tool the terminal CC bonds were selected and the derivative of the bonds specified as output. A TS(berny) optimisation was carried out at the HF 3-21G level of theory, with opt=noeigen specified as an additional keyword. This took the minimised energy structure from b. and optimised it to a TS(berny). This preserved the bond lengths and angles achieved in the energy minimisation calculation of part b., and allowed only the distance between the terminal carbons to reach a length corresponding to minimum energy.
Results (force constant specified "never"):
E(RHF) = -231.61932220 a.u. RMS Gradient Norm = 0.00010171 a.u. Dipole Moment = 0.0004 Debye Point Group = C2h
| Fragment Involved | Bond | Bond Length (A) | Bond Angle | Angle (degrees) |
| Fragment 1 | C1-C2 | 1.38849 | C1-C2-C3 | 120.52267 |
| C2-C3 | 1.38849 | |||
| Inter-fragment distances | terminal C1-C1 | 2.02214 | ||
| terminal C3-C3 | 2.02214 | |||
| Fragment 2 | C1-C2 | 1.38849 | C1-C2-C3 | 120.52267 |
| C2-C3 | 1.38849 | |||
Results (force constant specified "once") TS using constraint and derivative of terminal CC bonds at the HF 3-21G level of theory
Calculation Type = FTS Calculation Method = RHF Basis Set = 3-21G Charge = 0 Spin = Singlet E(RHF) = -231.61932233 a.u. RMS Gradient Norm = 0.00002113 a.u. Imaginary Freq = 1 Dipole Moment = 0.0001 Debye Point Group = C2h
| Fragment Involved | Bond | Bond Length (A) | Bond Angle | Angle (degrees) |
| Fragment 1 | C1-C2 | 1.3893 | C1-C2-C3 | 120.52849 |
| C2-C3 | 1.38929 | |||
| Inter-fragment distances | terminal C1-C1 | 2.02071 | ||
| terminal C3-C3 | 2.02071 | |||
| Fragment 2 | C1-C2 | 1.3893 | C1-C2-C3 | 120.52891 |
| C2-C3 | 1.38929 | |||
Both these structures agree with the energy of the no.3 TS, thus it can be deduced that this is a TS. The RMS gradients are larger for these structures than for the no.3 TS, although the RMS gradient is lower for the calculation run with force constant calculated "once" than for "never", indicating that the former method is more accurate when approximating a TS. The no.3 TS was used in following calculations as it was deemed most accurate due to the low RMS gradient.
e. Arranged and numbered anti Ci 1,5-butene for combination in the boat transition state as illustrated.
Boat transition resembles a dissociated boat, as shown in the following figure, with no expected overlapping of CC bonds. Terminal CC1 bond length =2.02097 A. Terminal CC2 bond=2.0205 A
Boat TS at the QST2 level of theory
Changed the approach of the anti Ci molecules as shown in the following figure.
This produced the following structure:
Boat TS optimised at HF 3-21G level of theory
E(RHF) = -231.60280246 a.u. RMS Gradient Norm = 0.00003615 a.u. Imaginary Freq = 1 Dipole Moment = 0.1583 Debye Point Group = C1
| Fragment Involved | Bond | Bond Length (A) | Bond Angle | Angle (degrees) |
| Fragment 1 | C1-C2 | 1.38145 | C1-C2-C3 | 121.6738 |
| C2-C3 | 1.3813 | |||
| Inter-fragment distances | terminal C1-C1 | 2.13988 | ||
| terminal C3-C3 | 2.14036 | |||
| Fragment 2 | C1-C2 | 1.38145 | C1-C2-C3 | 121.68917 |
| C2-C3 | 1.3815 | |||
One imaginary frequency was exhibited at -839.93, (IR 1.6119; Raman Activity of 27.0173). The imaginary vibration (the reaction path) is shown below.

This is indicative of an asynchronous reaction mechanism, as the forming bond constriction and breaking bond lengthening occur separately, not simultaneously.
To find the activation energy at the HF 3-21G level of theory, the specified product/reactant geometry was optimised to a minimum. This gave the gauche3 conformer, with results shown below.
gauche3 product of boat TS asynchronous mechanism
E(RHF) = -231.69266117 a.u. RMS Gradient Norm = 0.00002308 a.u. Imaginary Freq = Dipole Moment = 0.3405 Debye Point Group = C1
This gives an activation energy of 0.0898593 a.u (56.387574121 kcal/mol). Despite this activation energy not being corrected for zero-point energy, to approximate the validity of the TS this Ea was compared with literature in Appendix II at 0 K, with a relative error of 1.42 %, indicating that a close approximation had been modelled.
QST3 Calculations Carried Out After the Calculation of Activation Energy. The TS structure from the QST2 calculation was entered into TS(QST3) optimisations using the anti2 conformer as reactant and product. This gave a first optimisation result reported below.
Boat TS QST3 first optimisation
Total Energy = -231.60280233 a.u. RMS Gradient Norm = 0.00002594 a.u. Imaginary Freq = 1 Dipole Moment = 0.1585 Debye
The final terminal CC inter-fragment bond length changes to: 2.13975 and 2.13971 A. This indicates that the TS is still slightly offset from the true TS, as the symmetry of the synchronous mechanism is not reflected in the unequal interaction lengths. This TS was entered into the TS(QST3) calculation again and the calculation repeated, giving a TS with parameters shown below.
Total Energy = -231.60280232 a.u. RMS Gradient Norm = 0.00003644 a.u. Imaginary Freq = 1 Dipole Moment = 0.1585 Debye
A further optimisation at this level of theory returned the same conformer, with the same RMS gradient norm, so it was deduced that the calculation had converged to the TS.
Total Energy = -231.60280232 a.u. RMS Gradient Norm = 0.00003644 a.u. Imaginary Freq = 1 Dipole Moment = 0.1585 Debye
The final terminal inter-fragment CC bond lengths change to 2.13970 and 2.13970 A. Thus the synchronicity of the mechanism is more apparent in the higher accuracy TS, as the symmetry of the bond formation is apparent in the equal interaction lengths. Thus this structure was deemed to have converged, due to no change in the TS energy following two optimisations, and was optimised to the DFT B3LYP level of theory to increase accuracy of the approximation. Results are below.
Boat TS QST3 convergence at DFT B3LYP level
E(RB3LYP) = -234.54309307 a.u. RMS Gradient Norm = 0.00000451 a.u. Dipole Moment = 0.0613 Debye Point Group = C1
terminal CC bond lengths:2.20661 and 2.20661 A. The bond lengths are longer when optimised to DFT B3LYP level of theory, an effect expected from observations made during previous optimisations.
Frequency calculations were carried out on this optimised structure at the DFT B3LYP level of theory, with one imaginary frequency being present at -530.37 cm-1, which is shown below.
This is a synchronous vibration, with contraction of forming bonds and elongation of breaking bonds occurring simultaneously, which reinforces the synchronicity of the concerted mechanism for the boat TS mechanism.
As an indication of the activation energy for the boat TS mechanism using the TS(QST3) method, the energy of the anti2 conformer and the energy of the boat TS were considered. The anti2 conformer was considered here as it was specified in as the reactant in the optimisation, unlike in the QST2 method which required the gauche3 conformer to be specified. This gave an electronic energy difference of 0.089733 (56.3083197 kcal/mol) at the HF 3-21G level of theory and 0.0686206 a.u (43.06008581 kcal/mol)for DFT B3LYP level. Thus the activation energy has decreased using the QST3 method c.f the QST2 method, with the mechanism appearing to change from asynchronous (QST2) to synchronous (QST3), and with a slight reduction in inter-fragment bond length. This indicates that the TS(QST3) method is more reliable than QST2, giving a more accurate approximation of the TS.
f. IRC (Intrinsic Reaction Coordinate) was modelled using the lowest energy TS from part b, as this gave the lowest RMS gradient, and provides the lowest energy, most favourable, and so most probable reaction path (as it requires the least energy to overcome). The IRC gives the steepest descent in energy down the PES from the TS to the product geometry. N was set to 50 as this reduced the energy over which each geometry was changed down the PES, reducing the probability of straying from the true reaction coordinate path, which curves down the PES, c.f. the IRC calculation which gives a linear descent.
On the optimised chair structure with lowest energy from part b.(improved no.3) IRC calculations were carried out, with transition state berny, and force constant calculated once.

with final state geometry and parameters of:
Final state on IRC curve geometry
Calculation Method = RHF Basis Set = 3-21G Charge = 0 Spin = Singlet Total Energy = -231.68603599 a.u. RMS Gradient Norm = 0.00136429 a.u. Imaginary Freq = 0 Dipole Moment = 0.2082 Debye Point Group = N/A
As shown, this did not give the expected stationary point at the end of the calculation, with RMS gradient norm being relatively large, and so the IRC was carried out with force constant being carried out always, with 70 points being specified on the curve. This gave 44 structures, with a parabolic decrease in energy to the local minimum stationary point, as shown below:

Point 1 structure: Lowest energy chair TS optimised to the HF 3-21g level of theory Charge = 0 Spin = Singlet E(RHF) = -231.61932246 a.u. RMS Gradient Norm = 0.00001082 a.u. Dipole Moment = 0.0001 Debye Point Group = C1
changes to point 1 structure are as follows:
Point 22 along the IRC: Mid-way geometry between TS and product Point 44 along the IRC may represent the product. As the product and the reactant molecules in the Cope Rearrangement are equivalent however, this also means that the reactant energy and geometry is acquired at point 44 along the IRC: Reactant/product geometry along IRC
Charge = 0 Spin = Singlet E(RHF) = -231.69157876 a.u. RMS Gradient Norm = 0.00015224 a.u. Dipole Moment = 0.3631 Debye Point Group = C1
A rough estimate of the activation energy is thus the energy given at point 44 (product/reactant energy) - energy given at point 1 (optimised TS at HF 3-21g level of theory) = 0.0722563 a.u. (45.34 kcal/mol). This compares poorly with the literature energy given in Appendix II,of 54.76 kcal/mol (percentage error = 17.20 %), indicating the true product had not been reached. Additionally, frequency analysis of the point 44 structure revealed one imaginary frequency. For the minimum energy on the IRC, there was expected to be 0 imaginary frequencies, as at the minimum, all other points on the PES are maxima.
The geometry at point 44 was optimised further (to a minimum at the HF 3-21G level of theory), as increasing the input number of points on the IRC did not extend the curve further than point 44. There were no imaginary frequencies found for the optimised structure, reinforcing it to be a minimum of the curve. IR spectrum is attached below.
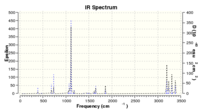
Results:
Charge = 0 Spin = Singlet E(RHF) = -231.69166702 a.u. RMS Gradient Norm = 0.00000029 a.u. Imaginary Freq = 0 Dipole Moment = 0.3805 Debye Point Group = C2
The reduction in the RMS Gradient Norm c.f. that for point 44 on the IRC indicates greater convergence of the optimised product c.f. point 44. The geometry of the optimised product is as shown below:
Reactant/product geometry along IRC after optimisation
This product/reactant geometry is equivalent to the gauche4 conformer, which does not exist as the lowest energy conformer. Using this conformer as the product/reactant gives a final chair TS synchronous mechanism activation energy of 0.0723446 a.u. (45.397 kcal/mol) HF 3-21G level of theory. As an approximation of the validity of this result, it was compared with literature in Appendix II at O K, with a small percentage relative error of 0.66 % indicating a good fit.
g. Chair TS: Optimised the HF 3-21g chair TS structure (improved no.3) to DFT B3LYP 6-31G* level of theory, results are as below.
improved no.3 allylic fragment TS optimised to DFT B3LYP level of theory
E(RB3LYP) = -234.55698303 a.u. RMS Gradient Norm = 0.00001192 a.u. Imaginary Freq = 1 Dipole Moment = 0.0000 Debye Point Group = C2h
As the RMS gradient is close to zero to 5 d.p, the optimisation had converged.
Geometry:
| Fragment Involved | Bond | Bond Length (A) | Bond Angle | Angle (degrees) |
| Fragment 1 | C1-C2 | 1.4075 | C1-C2-C3 | 119.95241 |
| C2-C3 | 1.4075 | |||
| Inter-fragment distances | terminal C1-C1 | 1.96755 | ||
| terminal C3-C3 | 1.96755 | |||
| Fragment 2 | C1-C2 | 1.4075 | C1-C2-C3 | 119.95241 |
| C2-C3 | 1.4075 | |||
Boat TS: optimised from HF to DFT B3LYP 6-31G* with results shown below.
optimisation of HF 3-21g chair TS to DFT B3LYP 6-31G
E(RB3LYP) = -234.54309307 a.u. RMS Gradient Norm = 0.00000448 a.u. Imaginary Freq = 1 Dipole Moment = 0.0613 Debye Point Group = C2h
Here, the RMS gradient is zero to 5 d.p, and thus the optimisation had converged, and a PES stationary point (local TS maxima) found.
Geometry:
| Fragment Involved | Bond | Bond Length (A) | Bond Angle | Angle (degrees) |
| Fragment 1 | C1-C2 | 1.39323 | C1-C2-C3 | 122.2702 |
| C2-C3 | 1.39323 | |||
| Inter-fragment distances | terminal C1-C1 | 2.20661 | ||
| terminal C3-C3 | 2.20661 | |||
| Fragment 2 | C1-C2 | 1.39323 | C1-C2-C3 | 122.2702 |
| C2-C3 | 1.39323 | |||
Activation Energy
The activation energies are as expected, with the chair TS mechanism giving a lower energy pathway than the boat TS.
Chair TS: Using the minimised energy of the gauche4 conformer of 1,5-butadiene at the DFT B3LYP level of theory, with energy of -234.61068823 a.u, this returned activation energy of 0.0537052 a.u (33.700529 kcal/mol) for chair TS. Despite not correcting for zero-point energy, as an approximation prior to further calculation, the chair activation energy compares well with literature at 0K from Appendix II, at 1.0555 % relative error.
Boat TS: Using the minimised energy of the gauche3 conformer (-234.61132934 a.u) at DFT B3LYP level of theory, the boat activation energy at 0 K was calculated at 0.0682363 a.u (42.81893387 kcal/mol). Despite not correcting for zero-point energy, as an approximation prior to further calculation, the boat activation energy compares well with literature at 0K at 2.047 % relative error. This agrees more poorly with the literature in Appendix II than the chair TS does, resulting from guess TS application to IRC. However, the most favourable reactant/product conformation was attained using the TS(QST2) method.
The TS electronic energies, thermochemistry parameters and activation energies are summarised below.
Activation energy at 0 K was calculated using the difference between reactant and TS electronic energy + zero-point energy. At all other temperatures the activation energy was calculated using the difference between the reactant and TS electronic energy + thermal energy.
Sum of energies at HF and DFT B3LYP level of theory
| ' | HF/ 3-21G | ' | ' | ' | ' | ' | ' | ' | ' | ' | ' | ' | ' | DFT B3LYP/6-31G* | ' | ' | ' | ' | ' | ' | ' | ' | ' | ' | ' | ' |
| Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Sum of electronic and thermal enthalpies | Sum of electronic and Gibbs Free Energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Sum of electronic and thermal enthalpies | Sum of electronic and Gibbs Free Energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Sum of electronic and thermal enthalpies | Sum of electronic and Gibbs Free Energy | Electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Sum of electronic and thermal enthalpies | Sum of electronic and Gibbs Free Energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Sum of electronic and thermal enthalpies | Sum of electronic and Gibbs Free Energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Sum of electronic and thermal enthalpies | Sum of electronic and Gibbs Free Energy | |
| at 0 K | at 0.1 K | at 0.1 K | at 0.1 K | at 0.1 K | at 298.15 K | at 298.15 K | at 298.15 K | at 298.15 K | at 400 K | at 400 K | at 400 K | at 400 K | at 0 K | at 0.1 K | at 0.1 K | at 0.1 K | at 0.1 K | at 298.15 K | at 298.15 K | at 298.15 K | at 298.15 K | at 400 K | at 400 K | at 400 K | at 400 K | |
| Chair TS | -231.6193225 | -231.4666985 | -231.4666985 | -231.4666975 | -231.4666985 | -231.4666985 | -231.4613395 | -231.4603955 | -231.3425805 | -231.4666985 | -231.4572935 | -231.4560265 | -231.5081634 | -234.556983 | -234.414929 | -234.414928 | -234.414928 | -234.414928 | -234.414929 | -234.414929 | -234.409009 | -234.408064 | -234.414929 | -234.404521 | -234.261201 | -234.314673 |
| Boat TS | -231.6028025 | -231.4509285 | -231.4509275 | -231.4509275 | -231.4509275 | -231.4509285 | -231.4452995 | -231.4443555 | -231.4797745 | -231.4509285 | -231.4411485 | -231.4398815 | -231.4925265 | -234.5430931 | -234.4023421 | -234.4023411 | -234.4023401 | -234.4023411 | -234.4023421 | -234.3960071 | -234.3950631 | -234.4317511 | -234.4023421 | -234.3913281 | -234.3900611 | -234.4450161 |
Activation energies at different temperature for the synchronous and asynchronous Cope Rearrangement
| Energy | HF/3-21G | HF/3-21G | HF/3-21G | HF/3-21G | B3LYP/6-31G* | B3LYP/6-31G* | B3LYP/6-31G* | B3LYP/6-31G* |
| at 0 K | at 0.1 K | at 298.15 K | at 400 K | at 0 K | at 0.1 K | at 298.15 K | at 400 K | |
| ΔE (Chair) (kcal/mol) | 44.93163696 | 44.93100946 | 43.96779235 | 43.76510888 | 33.16726092 | 33.16726092 | 32.32452439 | 32.14505853 |
| ΔE (Boat) (kcal/mol) | 55.5696263 | 55.5696263 | 54.81034767 | 54.6716695 | 41.63562098 | 41.63562098 | 41.0746333 | 41.0125105 |
| ΔE (Chair) (a.u/particle) | 0.07160386 | 0.07160286 | 0.07006786 | 0.06974486 | 0.05285594 | 0.05285594 | 0.05151294 | 0.05122694 |
| ΔE (Boat) (a.u/particle) | 0.08855675 | 0.08855675 | 0.08734675 | 0.08712575 | 0.06635127 | 0.06635127 | 0.06545727 | 0.06535827 |
| gauche3 | -231.5394852 | -231.5394842 | -231.5326462 | -231.5282742 | -234.4686933 | -234.4686923 | -234.4614643 | -234.4566863 |
| boat | -231.4509285 | -231.4509275 | -231.4452995 | -231.4411485 | -234.4023421 | -234.4023411 | -234.3960071 | -234.3913281 |
| gauche4 | -231.5383023 | -231.5383013 | -231.5314073 | -231.5270383 | -234.467785 | -234.467784 | -234.460522 | -234.455748 |
| chair | -231.4666985 | -231.4666985 | -231.4613395 | -231.4572935 | -234.414929 | -234.414928 | -234.409009 | -234.404521 |
Thus it can be seen that increasing the temperature reduced the activation energy for both chair and boat TS mechanisms. From the Arrhenius equation it follows that the decrease in activation energy would bring about an increase in rate, as rate is proportional to: exp(-Ea/RT). This decrease in activation energy is expected as through kinetic theory, the speed of molecule motion is increased at increased temperatures. At higher temperatures, more molecules have a higher vibrational, translational and rotational status, with more dregrees of freedom being accessed due to the higher energy available to molecules at higher temperatures. Using collision theory, this allows for increased collisions between molecules per unit time with increased temperature, thus giving increased rate of reaction as more collisions per unit time results in more potential molecular interactions and so successful reactions between the reacting molecules. This is witnessed as a decrease in activation energy as the energies of each collision is higher, and so less energy is required by the reacting pair to overcome the potential barrier. This increase in reaction rate can be approximated with the exponential factor of the Arrhenius equation, and calculating this using the activation energies found at each temperature for the chair and boat mechanisms, t each respective level of theory. In this way, it can be found that rate of reaction is greater for the increased level of theory (in this case DFT B3LYP), and is greater at increased temperature.
| ' | Exponential Factors in the Arrhenius Equation Using Activation Energy | ' | ' | ' |
| Level of theory | HF/3-21G | HF/3-21G | DFT B3LYP/6-31G* | DFT B3LYP/6-31G* |
| Temperature | at 298.15 K | at 400 K | at 298.15 K | at 400 K |
| ΔE (Chair) (kcal/mol) | 5.9072E-33 | 1.2256E-24 | 2.0228E-24 | 2.7359E-18 |
| ΔE (Boat) (kcal/mol) | 6.6640E-41 | 1.3471E-30 | 7.7998E-31 | 3.9107E-23 |
Appendix I for Calculating TS Thermochemistry Boat Transition State Temp. 298.15 Kelvin, Pressure = 1 atm, frequencies scaled by 0.8929. The molecule was calculated as an asymmetric top, with rotational symmetry number = 1. Zero point vibrational energy = 329948.6 Joules/mol = 78.85960 kcal/mol
| Energy Correction | Energy (a.u/Particle) |
| Zero-point correction | 0.125671 |
| Thermal correction to energy | 0.132653 |
| Thermal correction to enthalpy | 0.133597 |
| Thermal correction to Gibbs Free Energy | 0.095828 |
| Energy | Energy (Thermal) (kcal/mol) | CV (cal/mol-Kelvin) | S (cal/mol-Kelvin) |
| Total | 83.241 | 27.584 | 79.49 |
| Electronic | 0 | 0 | 0 |
| Translational | 0.889 | 2.981 | 39.129 |
| Rotational | 0.889 | 2.981 | 26.589 |
| Vibrational | 81.463 | 21.623 | 13.772 |
Reran calculation at 0.1 K. Chair TS gave zero-point vibrational energy of 333001.7 joules/mol, 79.58931 kcal/mol and energy/enthalpy corrections of:
| Energy Correction | Energy (a.u/Particle) |
| Zero-point correction | 0.126834 |
| Thermal correction to energy | 0.126835 |
| Thermal correction to enthalpy | 0.126835 |
| Thermal correction to Gibbs Free Energy | 0.126835 |
| Energy | Energy (Thermal) (kcal/mol) | CV (cal/mol-Kelvin) | S (cal/mol-Kelvin) |
| Total | 79.59 | 5.962 | 1.904 |
| Electronic | 0 | 0 | 0 |
| Translational | 0 | 2.981 | -0.616 |
| Rotational | 0 | 2.981 | 2.52 |
| Vibrational | 79.589 | 0 | 0 |
Boat TS was also run at 0.1 K, with zero-point vibrational energy at 329948.6 joules/mol and 78.8596 kcal/mol. Energy/enthalpy correction results as follows:
| Energy Correction | Energy (a.u/Particle) |
| Zero-point correction | 0.125671 |
| Thermal correction to energy | 0.125672 |
| Thermal correction to enthalpy | 0.125672 |
| Thermal correction to Gibbs Free Energy | 0.125672 |
| Energy | Energy (Thermal) (kcal/mol) | CV (cal/mol-Kelvin) | S (cal/mol-Kelvin) |
| Total | 78.86 | 5.962 | 2.127 |
| Electronic | 0 | 0 | 0 |
| Translational | 0 | 2.981 | -0.616 |
| Rotational | 0 | 2.981 | 2.742 |
| Vibrational | 78.86 | 0 | 0 |
The Diels Alder Cycloaddition
Notes: HOMO-LUMO need to have equivalent symmetry and similar energy. Electron withdrawing group on dienophile lowers energy of LUMO, electron donating group on diene to raise HOMO.
1. Drew cis-butadiene with sigma bond length 1.48 A and pi bond length 1.34 A as reported in literature.[4].
Calculation Type = FOPT Calculation Method = RAM1 Basis Set = ZDO Charge = 0 Spin = Singlet E(RAM1) = 0.04879719 a.u. RMS Gradient Norm = 0.00001745 a.u. Imaginary Freq = Dipole Moment = 0.0414 Debye Point Group = C2v
Bond lengths:
| Bond | Bond Length (Angstrom) |
| C1/3-C2/4 | 1.3351 |
| C2-C3 | 1.4494 |
| C1-H1 | 1.09776 |
| C2-H2 | 1.10528 |
| C3-H3 | 1.4494 |
| C4-H4 | 1.09776 |
Optimisation had converged to the lowest energy conformation of cis-butadiene at this level of theory due to the zero RMS gradient norm.
Tried to optimise this structure further using AM1, giving a C2 symmetry geometry with higher energy than the constrained C2V geometry initially obtained. This is shown below:
further optimisation of butadiene at AM1 level of theory
Calculation Type = FOPT Calculation Method = RAM1 Basis Set = ZDO Charge = 0 Spin = Singlet E(RAM1) = 0.04878534 a.u. RMS Gradient Norm = 0.00000090 a.u. Imaginary Freq = Dipole Moment = 0.0353 Debye Point Group = C2
The C2v geometry, with the lowest energy, is the most stable of the modelled conformations an was thus be used in the following calculations.
The HOMO and LUMO were visualised, and the alpha MO energies and structure are as attached.

The HOMO:

The LUMO:
tHE LUMO shown with mesh structure:
The HOMO is anti-symmetric w.r.t the sigma v plane, and the LUMO is symmetric w.r.t the sigma v plane. The terminal CC bond lengths between ethene and cis-bet-2-ene are as follows: 2.11931 and 2.11917 A.
Higher Levels of Theory: To increase the accuracy of these calculations the TS was optimised to HF and through to DFT B3LYP level of theory, with results shown below.
i. The butadiene structure optimised to a minimum at AM1 level of theory was optimised to HF 3-21G level of theory, from which it was further optimised to DFT B3LYP 6-31G*. The results associated with this structure are documented below:
optimisation of butadiene to DFT B3LYP 6-31G* level of theory
Calculation Type = FOPT Calculation Method = RB3LYP Basis Set = 6-31G(d) Charge = 0 Spin = Singlet E(RB3LYP) = -155.98594952 a.u. RMS Gradient Norm = 0.00005672 a.u. Imaginary Freq = 0 Dipole Moment = 0.0850 Debye
Bond lengths (A): C1-C2 = 1.33982; C2-C3 = 1.47147; C3-C4 = 1.33982
The shorter terminal CC bond lengths agree with literature alkene bond lengths of ~1.34 A,
[5]
indicating the optimised structure favours localisation of the pi clouds to the two terminal CC bonds. The central CC bond is typical of sp2-sp2 C-C bonds.[5] The structure is similar to that at AM1 theory, with C2v symmetry preservation.
b. The TS of the Diels Alder cycloaddition was modelled on the cis-1,5-butadiene and ethene reagents. The TS of the reaction was modelled using cis-but-2-ene and ethane, with these groups forming an interaction at 2.2 A distance between the terminal carbons of these groups. 2.2 A was chosen as this provided a rough aproximate of most typical Diels-Alder reactions, such as those cyclopentadienyl.[6]
AM1 optimisation was carried out, with opt=noeigen as the calculation would not run without this being specified in the additional keywords. Results of this optimisation are as shown below.
Terminal CC bond lengths = 2.11918 and 2.11933 A Calculation Type = FTS Calculation Method = RAM1 Basis Set = ZDO Charge = 0 Spin = Singlet E(RAM1) = 0.11165466 a.u. RMS Gradient Norm = 0.00000998 a.u. Imaginary Freq = Dipole Moment = 0.5605 Debye Point Group = Cs
The structure of the guess TS is as shown below: optimisation of Diels-Alder TS to AM1 level of theory
with VdW radii as shown below: optimisation of Diels-Alder TS to AM1 level of theory VdW radii shown
Frequency calculations were carried out at this TS with opt=noeigen specified in the additional keywords. This gave an imaginary frequency of -956.33, 5.6150 in the IR. The TS(berny) vibration at this frequency and the IR spectrum are as shown.
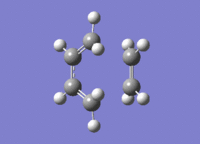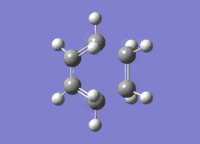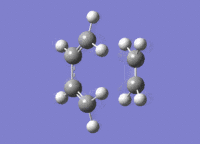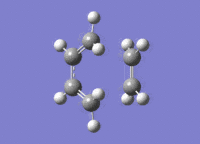

The TS was optimised to a minimum at the AM1 level of theory with the terminal CC bonds frozen at length 2.2 A with results as shown below. This was done to verify the validity of the guess TS(berny). The minimised energy TS is as shown below, with parameters as follows:
Calculation Method = RAM1 Basis Set = ZDO Charge = 0 Spin = Singlet E(RAM1) = 0.10745376 a.u. RMS Gradient Norm = 0.00617994 a.u. Imaginary Freq = 1 Dipole Moment = 0.4155 Debye Point Group = C1
There is one imaginary frequency of -420.03, IR 9.4469, with vibration shown below.
IR spectrum is as shown:
Optimised this minimised guess TS by derivatising the terminal CC bonds. This gave CC terminal bond lengths of 2.11996 and 2.11907 A.
Parameters associated with the structure are reported:
Calculation Type = FREQ Calculation Method = RAM1 Basis Set = ZDO Charge = 0 Spin = Singlet E(RAM1) = 0.11165483 a.u. RMS Gradient Norm = 0.00003723 a.u. Imaginary Freq = 1 Dipole Moment = 0.5598 Debye Point Group = C1
The reaction vibration occurs at -955.85, IR 5.5951, and is shown below with the IR spectrum.
The lowest positive energy vibration is observed as:

The reaction vibration (at the imaginary frequency) depicts a synchronous TS, which agrees with literature reports. The lowest frequency vibration depicts an asynchronous vibration, but this is not accessed as the reaction pathway. [5]
As the guess TS lies at 0.11165466 a.u and 0.11165483 a.u for the alternative method of approaching the TS, energies equal to 5 d.p, the TS of the Diels Alder lies at this energy. The lowest energy TS was used for following calculations as this provided the smallest gradient (RMS norm), and so the most probable barrier for reaction.
Higher Levels of Theory: To increase the accuracy of these calculations the TS was optimised to HF and through to DFT B3LYP level of theory, with results shown below.
ii. The lowest energy TS obtained from the AM1 level of theory optimisation (TS(berny)) was used in optimisation to HF 3-21G level of theory. This gave a geometry change illustrated below:
optimisation of TS to HF 3-21G level of theory
Total Energy = -231.60320857 a.u. RMS Gradient Norm = 0.00000494 a.u. Dipole Moment = 0.5755 Debye
Geometry:
| species | Bond | Bond length (A) |
| butadiene | C1=C2 | 1.37001 |
| C2-C3 | 1.39446 | |
| C3=C4 | 1.38308 | |
| interfragment | terminal C1-C1 | 2.20961 |
| terminal C2-4 | 2.20959 | |
| ethylene | C1-C2 | 1.37587 |
From this structure, optimisation to TS(berny) at DFT B3LYP 6-31G* optimisation was carried out, with results below.
Geometry of Diels-Alder TS(berny) optimised through AM1-HF 3-21G-DFT B3LYP 6-31G* levels of theory
E(RB3LYP) = -234.54389651 a.u. RMS Gradient Norm = 0.00002396 a.u. Dipole Moment = 0.3947 Debye Point Group = Cs
Geometry:
| species | Bond | Bond length (A) |
| butadiene | C1=C2 | 1.38319 |
| C2-C3 | 1.34072 | |
| C3=C4 | 1.38308 | |
| interfragment | terminal C1-C1 | 2.27228 |
| terminal C2-4 | 2.27209 | |
| ethylene | C1-C2 | 1.38606 |
The ethylene CC bond length is roughly equal to the 1.4 A reported in literature.[6] This indicates the acceptance of electrons into the pi* orbital from butadiene and donation of pi electrons by ethylene. Lengthening of the terminal butadiene CC bonds by ~0.05 A each indicates the breaking of the pi bonds through donation of ethylene pi electron density and butadiene C2/3 pi electron density into pi* clouds. This delocalisation of charge across the butadiene molecule is reinforced by the ~0.07 A decrease in C2-C3 length which signifies a reorientation of C2 and C3 p orbitals, allowing pi overlap and increase in strength of the central bond. The increased attraction between the more strongly overlapping C2 and C3 p orbitals results in the observed contraction. This delocalised pi cloud approximation is reinforced through agreement of observed bond lengths with literature reports of those of benzene.[5]
This geometry is proven to be a TS by the single imaginary frequency at -526.21 (IR 5.7949), the vibration for which, and the TS IR spectrum are shown below:

The similarity of the TS vibrational structure, and the imaginary vibration, at this higher level of theory c.f. AM1 calculation results indicates that the reaction coordinate still proceeds in a synchronous concerted manner, with the ethylene approaching butadiene in a syn-manner; bond formation and bond breaking occurring simultaneously across the whole molecule.
Using the Gaussian 09W FreqChq tool, the correction energies were found at 298.15 and 400 K for the HF and DFT B3LYP level of theory calculations. These are reported in the table below.
Corrections to electronic energy at different temperatures:
| ' | HF/3-21G | ' | ' | ' | ' | ' | ' | ' | ' | ' | DFT B3LYP/6-31G* | ' | ' | ' | ' | ' | ' | ' |
| electronic energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Sum of electronic and thermal enthalpies | Sum of electronic and Gibbs Free Energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Sum of electronic and thermal enthalpies | Sum of electronic and Gibbs Free Energy | electronic energy | electronic energy at 0 K | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Sum of electronic and thermal enthalpies | Sum of electronic and Gibbs Free Energy | Sum of electronic and zero-point energies | Sum of electronic and thermal energies | Sum of electronic and thermal enthalpies | Sum of electronic and Gibbs Free Energy |
| at 298.15 K | at 298.15 K | at 298.15 K | at 298.15 K | at 400 K | at 400 K | at 400 K | at 400 K | at 0K | at 298.15 K | at 298.15 K | at 298.15 K | at 298.15 K | at 400 K | at 400 K | at 400 K | at 400 K | ||
| -231.6032086 | -231.4513386 | -231.4456506 | -231.4447056 | -231.4802786 | -231.4513386 | -231.4414696 | -231.4402026 | -231.4930876 | -234.648295 | -234.507723 | -234.507723 | -234.501307 | -234.500362 | -234.537289 | -234.507723 | -234.800015 | -234.495308 | -234.550642 |
Bond Length Analysis of Most Favourable Transition State Bond length of sigma C-C bond (sp3-sp3 hybridised carbons) is 1.54 A. The VdW radius of carbon is 1.7 A.[7] This gives the sum of the VdW radii of two non-overlapping Carbons as 3.4 A. The distance between the terminal carbons in the most favourable, lowest energy TS is 2.11918 and 2.11933 A. Thus, the VdW radii of the two carbons are overlapping. As the distance between the two carbons is ~0.4 A higher than the VdW radii of each carbon, this results in a favourable VdW attraction, not a repulsion. The interaction is at a greater length than a sigma bond, and so the terminal CC bonds have not yet formed, but the favourable VdW causes contraction of this interaction bringing it towards a single CC bond length and bond formation.
MOs and Bonding: The MOs involved in the Diels Alder cycloaddition include the ethylene pi and pi* HOMO and LUMO, which are as shown below.

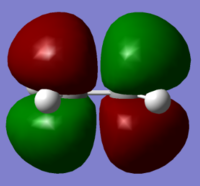
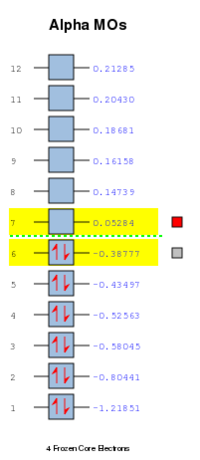
The energies of these orbitals were calculated at the AM1 level of theory to comply with butadiene and TS calculations, and are as noted below.
The transition state HOMO and LUMO orbitals are depicted below respectively:
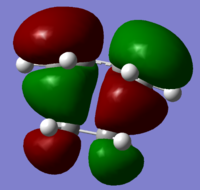
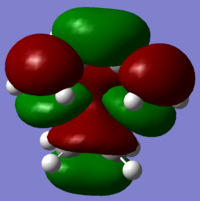
This confirms that the HOMO of ethylene and the LUMO of butadiene are both symmetric and that the LUMO of ethylene and the HOMO of butadiene are both antisymmetric w.r.t the sigma v plane. As the TS HOMO is antisymmetric, the orbitals combined to make it must also be antisymmetric (only orbitals of the same symmetry may combine). Hence the TS HOMO is the result of an interaction between the LUMO of ethylene and the HOMO of butadiene. The same rule applies for the LUMO, which is the result of an interaction between the HOMO of ethylene and the LUMO of butadiene. This assignment was further reinforced through an appreciation of the HOMO and LUMO energies of all species involved, and is summarised in the following MO diagram.
IRC Calculations IRC calculations were carried out at the AM1 level of theory. Force constant was calculated always, with N=50, opt=noeigen being specificed in additional keywords as the calculation would not run due to the imaginary frequency being present.
The IRC is shown below:
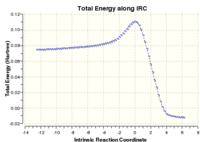
This shows the TS at point 51 clearly as a maximum of potential energy on the energy curve. The curve starts somewhere along the reaction coordinate as point 1 has 2 imaginary frequency at -50 and -26.82 and is therefore not a minimum of energy, as expected of reactants. Reactant geometry and imaginary vibrations are shown below:
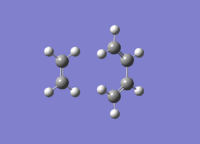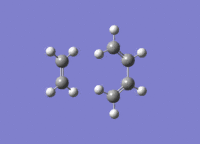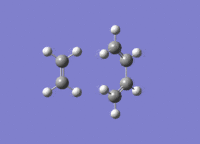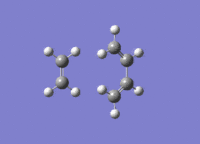
Parameters associated with reactants: Charge = 0 Spin = Singlet E(RAM1) = 0.07535669 a.u. RMS Gradient Norm = 0.00018607 a.u. (not a minimum as doesn't equal 0 to 5 d.p) Dipole Moment = 0.0349 Debye Point Group = Cs
The product formed at point 76 was not the minimum of the curve, indicated by the presence of an imaginary frequency of -43.09 at this point.
This is reinforced by the decreasing energies (and >0 RMS gradients) of points 74, 75 and 76 at -0.01082131 a.u (RMS Gradient Norm = 0.00023409 a.u),-0.01094016 a.u.(RMS Gradient Norm = 0.00014584 a.u) and -0.01099165 a.u.(RMS Gradient Norm = 0.00009819 a.u) each, respectively.
Additionally, upon conformational analysis it became apparent that this Cs structure existed in envelope-like conformation, with two sets of eclipsed CC bonds.
Bond lengths (A): C1=C6: 1.33796; C1-C2/C5-C6 = 1.48351, C2-C3/C4-C5 = 1.51880, C3-C4 = 1.51852
The envelope-like conformer with eclipsed alkyl groups is reported to be higher in energy than the half-chair conformer with staggered alkyl groups, due to reduced sigma conjugation and increased steric clashing of the large carbon atoms of the envelope-like structure. [8]
To find the minimum of the curve, the geometry at point 76 was optimised to a minimum at AM1 level of theory, giving a final C2 product geometry of lower energy as illustrated below:
optimised product at AM1 level of theory
Bond lengths (A): C1=C6: 1.33668; C1-C2/C5-C6 = 1.48351,C2-C3/C4-C5 = 1.51702,C3-C4 = 1.51441.
Upon conformational analysis it became apparent that this structure existed in a chair-like anti-periplanar conformation around the C3-C4 sigma bond. The alkyl groups occur gauche to each other c.f. the high energy syn-periplanar conformation of the non-optimised product geometry.
E(RAM1) = -0.01619491 a.u. RMS Gradient Norm = 0.00001375 a.u. Imaginary Freq = 0 Dipole Moment = 0.1831 Debye
This was optimised to HF 3-21G level of theory. Results are as below.
E(RHF) = -231.72915197 a.u. RMS Gradient Norm = 0.00001626 a.u. Dipole Moment = 0.2008 Debye Point Group = C1
And further optimised to DFT B3LYP 6-31G* level of theory. Results are as below.
E(RB3LYP) = -234.64829495 a.u. RMS Gradient Norm = 0.00001691 a.u. Dipole Moment = 0.2278 Debye Point Group = C1
Thus, as the product of the reaction was identified to adopt the half-chair conformation adopted by cyclohexene, as reported in literature,[8] it was deduced that this represented a possible product to the reaction.
TS(QST2) and TS(QST3) calculations:
In order to verify the correct identification of the TS, the reactants and products were input into a TS(QST2) calculation at HF 3-21 level of theory. This however failed (after multiple repeats and troubleshooting of problems). It was deduced that the TS was too "far away" on the PES from the reactants and products to be able to identify by the fully automated TS(QST2) method. The QST3 method was used, with the guess TS as input into the optimisation. Results are shown below.
Results:
Initial TS guess structure:
jmolFile text="Ts HF TS(berny) optimisation output, TS(QST3)optimisation at HF level of theory 1st opt">Ts hf trial 1.mol</jmolFile>
Total Energy = -231.60320851 a.u. RMS Gradient Norm = 0.00001765 a.u. Dipole Moment = 0.5753 Debye
Geometry:
| species | Bond | Bond length (A) | Bond Angle | Angle (degrees) |
| butadiene | C1=C2 | 1.36999 | C1-C2-C3 | 121.46622 |
| C2-C3 | 1.39445 | C2-C3-C4 | 121.46622 | |
| C3=C4 | 1.36997 | |||
| interfragment | terminal C1-C1 | 2.20961 | terminal C1-C1-C2 | 101.58751 |
| terminal C2-4 | 2.209621 | terminal C2-C4-C3 | 101.59707 | |
| ethylene | C1-C2 | 1.37585 | ||
This was optimised another further 2 times using the same reactant and product geometries, as the energy converged to -231.60320857 to 7 d.p, with results as shown.
2nd optimisation:
Ts HF TS(berny) optimisation output, TS(QST3)optimisation at HF level of theory 2nd opt
E(RHF) = -231.60320857 a.u.
RMS Gradient Norm = 0.00000175 a.u.
Dipole Moment = 0.5757 Debye
Point Group = C1
3rd optimisation:
Ts HF TS(berny) optimisation output, TS(QST3)optimisation at HF level of theory 3rd opt
Total Energy = -231.60320857 a.u. RMS Gradient Norm = 0.00000325 a.u. Imaginary Freq = Dipole Moment = 0.5757 Debye
One imaginary frequency was calculated at -818.37 cm-1
TS structure following constraint-derivative optimisation:
Ts HF constraint-derivative output TS(QST3)optimisation at HF level of theory
Total Energy = -231.60320856 a.u. RMS Gradient Norm = 0.00000915 a.u. Imaginary Freq = Dipole Moment = 0.5756 Debye
Geometry:
| species | Bond | Bond length (A) | Bond Angle | Angle (degrees) |
| butadiene | C1=C2 | 1.37 | C1-C2-C3 | 121.46903 |
| C2-C3 | 1.39444 | C2-C3-C4 | 121.46901 | |
| C3-C4 | 1.37001 | |||
| interfragment | terminal C1-C1 | 2.20962 | terminal C1-C1-C2 | 101.59738 |
| terminal C2-4 | 2.20962 | terminal C2-C4-C3 | 101.60121 | |
| ethylene | C1-C2 | 1.37587 | ||
One imaginary frequency was found at -818.22 cm-1, as shown below.
This structure was planned to have been optimised a further 2 times to allow for convergence of TS energy, but this would not run. After multiple repeats and troubleshooting of the calculation further TS(QST3) could not be run. The zero RMS gradient to 5 d.p however indicated that convergence was sufficient to approximate the TS in this case.
Thus it was deduced that the TS at -231.60320857 a.u (HF 3-21G level of theory) corresponded to the minimum of convergence, as the lowest RMS gradient occurs for this TS. Additionally, this agrees with the TS calculated using the guess TS method.
iii. Maleic Anhydride + Cyclohexadiene Cyclohexadiene reactant geometry was optimised to a minimum at the AM1 level of theory. Parameters and structure are shown below.
Charge = 0 Spin = Singlet E(RAM1) = 0.02771129 a.u. RMS Gradient Norm = 0.00000562 a.u. Imaginary Freq = 0 Dipole Moment = 0.4313 Debye Point Group = C2
Maleic anhydride geometry was optimised to a minimum at the AM1 level of theory. Parameters and structure are shown below.
Charge = 0 Spin = Singlet Total Energy = -0.12182418 a.u. RMS Gradient Norm = 0.00003683 a.u. Imaginary Freq = Dipole Moment = 4.5779 Debye Point Group = C2h
Optimisation was carried out for the TS(QST2) calculation, with reactants and products as specified below:
This gave an unreal TS, due to the vibrational frequency being higher than expected, with a vibration that didn't match any literature reports of the concerted synchronous mechanism.
This was deduced to be due to the reactant specification lying at a point somewhere along the PES, giving a TS that occurs after bond breaking and formation.
Charge = 0 Spin = Singlet Total Energy = -0.05041977 a.u. RMS Gradient Norm = 0.00001885 a.u. Imaginary Freq = Dipole Moment = 5.5646 Debye Point Group = Cs
Final terminal CC bond length of 1.53617 A and 1.53606 A.
The QST2 transition state method was carried out, using the optimised reactants and optimised products at the AM1 level of theory. Reactants and products were arranged as:

This gave a TS structure of: QST2 TS This has one imaginary frequency at -812.35 (IR 96.8538), with vibrational structure as shown below.
This shows a reaction vibration which involved synchronous bond breaking and formation with the approach of the anhydride double bond to the diene.
Charge = 0 Spin = Singlet Total Energy = -0.15990940 a.u. RMS Gradient Norm = 0.00000744 a.u. Imaginary Freq = 1 Dipole Moment = 5.2580 Debye
As the transition state energy is higher here than for the initial QST2 calculation, it was reinforced that the transition state modelled earlier lay at a point after the true TS, somewhere on the descent from TS to products.
Taking This Further The exo product was reoptimised at the HF 3-21G level of theory, as this was to be entered into a QST3 TS optimisation calculation in order to check the identification of the correct TS. The HF 3-21G level structure has parameters shown below. Exo Product HF level Charge = 0 Spin = Singlet E(RHF) = -605.71873541 a.u. RMS Gradient Norm = 0.00001203 a.u. Imaginary Freq = Dipole Moment = 5.8133 Debye Point Group = Cs
This structure was optimised to the DFT B3LYP 6-31G* level. This structure was not used in the QST3 calculation as it was deduced that the calculation would take too long to run at the higher level of theory. Parameters are shown below. Exo Product DFT level
Charge = 0 Spin = Singlet Total Energy = -612.75578546 a.u. RMS Gradient Norm = 0.00001511 a.u. Imaginary Freq = Dipole Moment = 4.7594 Debye
The exo TS was optimised to HF 3-21G level of theory, giving structure and parameters as shown below: QST2 optimised TS HF level
Charge = 0 Spin = Singlet E(RHF) = -605.60359125 a.u. RMS Gradient Norm = 0.00000658 a.u. Imaginary Freq = Dipole Moment = 5.9372 Debye Point Group = Cs
QST3 method at HF 3-21G level of theory: The input for the guess exo TS was the guess TS obtained from the QST2 method, and the reactant input for the QST2 method was the same as for the QST2 method.
Results: QST3 HF level
Terminal CC bond lengths (A):2.26070 and 2.26075 Charge = 0 Spin = Singlet E(RHF) = -605.60359125 a.u. RMS Gradient Norm = 0.00000077 a.u. Imaginary Freq = 1 Dipole Moment = 5.9369 Debye Point Group = Cs
This was optimised to the DFT B3LYP 6-31G* level of theory. Results: QST3 DFT level
Terminal CC bond lengths (A):2.29062 and 2.29063 Charge = 0 Spin = Singlet E(RB3LYP) = -612.67931089 a.u. RMS Gradient Norm = 0.00000804 a.u. Imaginary Freq = 1 Dipole Moment = 5.5494 Debye Point Group = Cs
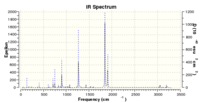
Vibrational analysis at the DFT B3LYP level was carried out: imaginary frequency at -448.44 (IR 5.5139)
IR spectrum:
Endo TS The endo TS was approximated using the TS of the exo, through rotation of the maleic anhydride so that the pi systems of both reagent species were directly above and below one another. This was cleaned, then optimised to TS(berny) at AM1 level of theory. Guess structure optimisation
charge = 0 Spin = Singlet Total Energy = -0.05150479 a.u. RMS Gradient Norm = 0.00001084 a.u. Imaginary Freq = 1 Dipole Moment = 6.1663 Debye Terminal CC Bond lengths:2.16242 and 2.16246 A.
One imaginary frequency was found, at -806.28 (IR 71.6105), which is as shown below.
From here, the TS was checked using the constraint and derivative method used previously. The two species were separated by 2.2 A terminal CC bonds, which were constrained during optimisation to a minimum. Results are as below:
TS resulting from frozen coordinates
Total Energy = -0.05238807 a.u. RMS Gradient Norm = 0.00271773 a.u. Dipole Moment = 6.0001 Debye
The TS was reoptimised, with the terminal CC bonds derivativised. This produced a TS(berny) as shown below.
Terminal CC bond lengths = 2.16233 and 2.16243 A. TS resulting from frozen and then derivatised coordinates
Parameters and structures: charge = 0 Spin = Singlet Total Energy = -0.05150479 a.u. RMS Gradient Norm = 0.00000804 a.u. Imaginary Freq = 1 Dipole Moment = 6.1662 Debye
The energies of these transition states are equivalent to >5 d.p. Thus the structure found represents the transition state of the endo reaction pathway, the latter structure being a better approximation of the TS due to the lower RMS gradient.
An IRC was to be carried out at AM1 level of theory, with the TS applied being the one obtained from using constraint and derivatising. This could not run using either guess TS or the final TS however, after multiple repeats and troubleshooting, error message always comes up as:
Charge and Multiplicity card seems defective: Wanted an integer as input.
It was deduced that the zero to 5 d.p RMS gradient indicated a sufficient convergence for procession to TS(QST3) calculations.
Taking This Further The endo product was obtained using the guess TS, making the appropriate bond type changes. This was optimised to a minimum at the HF 3-21G level of theory. Parameters and structure are as shown below: endo HF level of theory Terminal CC bond lengths (A):2.72772 and 2.72275
Charge = 0 Spin = Singlet E(RHF) = -605.72132084 a.u. RMS Gradient Norm = 0.00001869 a.u. Imaginary Freq = Dipole Moment = 6.0442 Debye Point Group = Cs
As for the exo product, this was optimised to the DFT B3LYP level of theory. Results are as shown below.
Charge = 0 Spin = Singlet E(RB3LYP) = -612.75829012 a.u. RMS Gradient Norm = 0.00001300 a.u. Imaginary Freq = Dipole Moment = 5.0199 Debye Point Group = C1
endo guess TS optimised to HF 3-21G: opt to HF level of theory Charge = 0 Spin = Singlet E(RHF) = -605.61036822 a.u. RMS Gradient Norm = 0.00002214 a.u. Imaginary Freq = 1 Dipole Moment = 6.7154 Debye Point Group = Cs
Frequency calcutions were carried out at HF 3-21G level of theory. This allowed electronic correction factors at 298.15 K to be calculated using the Gaussian 09W FreqChq tool. Results are shown below in the following table.
| HF/3-21G | ' | ' | ' | ' |
| electronic energy | electronic energy + zero-point correction | electronic energy + thermal correction | electronic energy + enthalpic correction | electronic energy+ Gibbs free energy correction |
| at 298.15 K | at 298.15 K | at 298.15 K | at 298.15 K | |
| -605.6103682 | -605.4149042 | -605.4054782 | -605.4045342 | -605.4501322 |
QST3 calculations: The input for the reactants was the same as for the exo QST3 calculation, the guess TS used was the TS obtained from the guess TS method and the endo product used was obtained from optimising the TS from the guess TS to a minimum.
Results: QST3 HF level of theory Terminal CC Bond lengths (A): 2.23077 and 2.23121 Charge = 0 Spin = Singlet E(RHF) = -605.61036822 a.u. RMS Gradient Norm = 0.00000412 a.u. Imaginary Freq = 1 Dipole Moment = 6.7142 Debye Point Group = Cs
As the QST3 TS optimisation returned the same energy as the guess TS method at the HF 3-21G level of theory, it can be deduced that the correct TS has been found. This TS was entered into an optimisation TS(berny) at DFT B3LYP 6-31G* level to approximate the energy of this TS to a higher, and thus more accurate level of theory.
Results: QST3 DFT B3LYP level of theory Terminal CC Bond lengths (A): 2.26846 and 2.26846
Charge = 0 Spin = Singlet E(RB3LYP) = -612.68339656 a.u. RMS Gradient Norm = 0.00001177 a.u. Imaginary Freq = Dipole Moment = 6.1138 Debye Point Group = Cs
Vibrational analysis at the DFT B3LYP level was carried out: imaginary frequency at -446.95 (IR 1.4418)
IR spectrum:
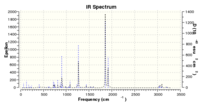
This lower energy TS at the DFT B3LYP level of theory is a closer approximation than the HF 3-21G equivalent calculated previously, as it takes into account the interaction of electrons. For both exo and endo TS the TS terminal CC bond lengths increase upon optimisation from HF to DFT B3LYP level of theory. Comparing the TS energy of the endo and exo pathways, the endo pathway returns a lower energy, and thus is the kinetic pathway. This is due to the due to secondary overlap of the carbonyl pi clouds and the allylic pi clouds, an effect which isn't present in the exo TS due to these pi clouds being too far apart to overlap effectively. Final product energies indicate that the thermodynamic product is the endo product also, which has a lower final energy at the DFT B3LYP 6-31G* level of theory. This may be due to increased steric clashing between the maleic anhydride functionality and the projecting hydrogens of the ethyl bridge present in the exo structure, which isn't present in the endo, as the ethylene bridge gives upward projecting hydrogens, which therefore do not clash with the maleic functional groups.
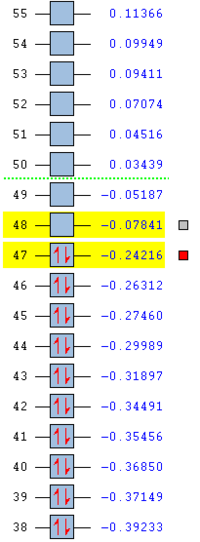
MO Analysis MO analysis of exo TS and reactants. Ordering and energy of the alpha MOs (at the DFT B3LYP level of theory)closest to the HOMO and LUMO are shown below.
The HOMO and LUMO are shown below resepctively. Both HOMO and LUMO are antisymmetric.
HOMO:
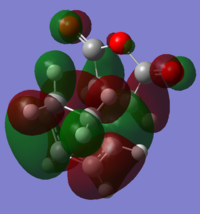
LUMO:
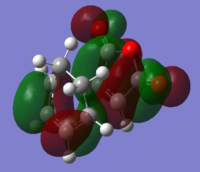
MO analysis of endo TS and reactants.
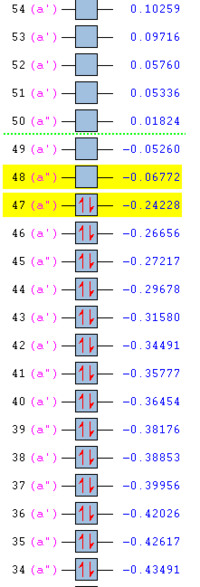
Ordering and energy of the alpha MOs (at the DFT B3LYP level of theory)closest to the HOMO and LUMO are shown below.
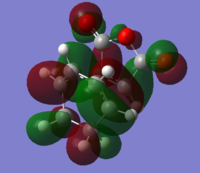
The HOMO and LUMO are shown below resepctively. Both HOMO and LUMO are antisymmetric
HOMO:

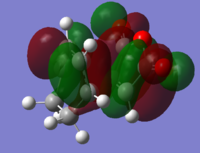
LUMO:
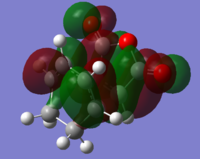
Comparison of HOMO-LUMO of endo TS and exo TS. In the HOMO of the exo TS, there is very limited overlap between the diene pi-clouds with the central oxygen p-like orbital. This is due to the small size of the central p-like oxygen orbital and large distance between this oxygen and the diene clouds. The diene clouds are antibonding in phase with the carbonyl oxygen pi-clouds. This effect is probably greater than any in-phase interaction with the central oxygen, as the pi clouds of the carbonyl oxygens are projecting upwards towards the diene clouds, whereas the central oxygen p-like orbital is projecting along the bonding plane, and is hence further in distance away from the diene clouds. The LUMO has a great antibonding interaction between the diene orbitals and the maleic anhydride carbon pi-like clouds. These orbitals shield the in-phase carbonyl oxygen p-like orbitals, which project upwards towards the diene, but are further away than the central carbon orbitals. This gives insufficient favourbale overlap to make up for the large antibonding interaction between the diene and the maleic anhydride central carbon pi-like orbitals, resulting in a large increase in energy between the HOMO and LUMO of the exo structure.
For the HOMO orbital in the endo structure, there is attractive secondary overlap of the diene electron clouds with the central oxygen p-like orbital cloud, which is larger than that in the exo HOMO and is closer to the diene clouds than in the exo structure by virtue of the endo state having the diene functionality lying directly over the maleic anhydride carbonyl groups. The diene orbitals are antibonding with respect to each other as for the exo TS, but as the oxygen p-like orbital projects through the bonding plane, each p-like lobe overlaps favourably with one in-phase allylic pi cloud. There is no net antibonding interaction between the diene clouds and the carbonyl clouds, as the carbonyl oxygen p-like orbitals lie in the bonding plane, and do not project towards the diene orbitals. This gives both a bonding and antibonding interaction with the diene, whcih cancels to zero net interaction between diene lobes and carbonyl oxygen lobes. Thus the HOMO of the endo state is lower in energy and more stabilised than the exo HOMO. In the LUMO the central oxygen does not have sufficient electron density to allow for interaction. The pi clouds of the maleic anydride carbons are directly overlapping in an antibonding fashion with those of the cyclohexadiene. There is limited in-phase overlap between the cyclohexadiene pi-clouds with the carbonyl oxygen pi-clouds, but this is weak in comparison due to increased distance between these overlapping clouds. These effects cause a large increase in energy from HOMO to LUMO, with the LUMO of the endo structure being lower than that of the HOMO by virtue of the reduced distance between the diene and the carbonyl oxygens.
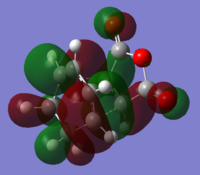
The increase in level of theory from AM1 to HF 3-21G to DFT B3LYP does not change the symmetry of the alpha MOs, only. To illustrate this the AM1 antisymmetric HOMO-LUMO are shown for the endo structure.
HOMO:
LUMO:
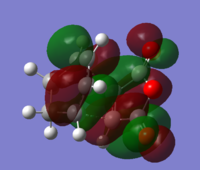
Through comparison with the AM1 and DFT B3LYP HOMO and LUMO, it can be seen that no change in symmetry occurs.The energy of the HOMO and LUMO however decrease in energy at the higher level of theory, along with the total molecule energy.The energy of the HOMO and LUMO decreases from 0.0734 and -0.32445 respectively at AM1 level, to -0.06772 and -0.24228 a.u respectively at DFT B3LYP.
Comparison of TS MOs with the reactant HOMO-LUMOs at DFT B3LYP 6-31G* level of theory. As with the TS HOMO-LUMO, all HOMO-LUMOs found for reactants were antisymmetric. Maleic anhydride MOs:
MO ordering:
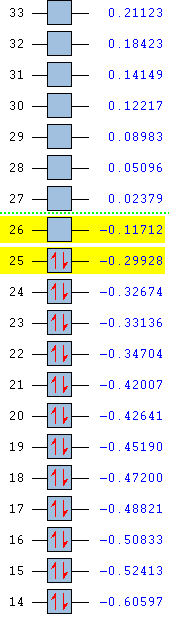
HOMO:
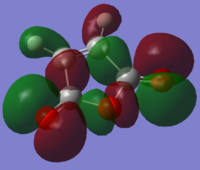
LUMO:
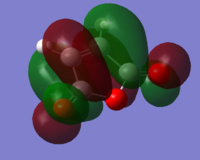
Cyclohexadiene MOs:
MO ordering:
HOMO:

LUMO:

Further Discussion I. Counter-ion and solvent effects are neglected in these Diels-Alder reactions as no solvent was specified in any of the calculations. It has been reported previously, [9] that solvent effects are important in cycloadditions such as Diels-Alder, with reactions acelerated (with lower TS energy and activation energy) when conducted in polar solvents.
This was investigated in the present study. Using the TS(QST3) method for the reaction between maleic anhydride and cyclobutadiene. Results are as below.
Exo TS(QST3) in water at HF level of theory:
QST3 in water exo TS HF level of theory
E(RHF) = -605.61895534 a.u. RMS Gradient Norm = 0.00002935 a.u. Imaginary Freq = Dipole Moment = 7.5135 Debye
Carrying out the Diels-Alder TS optimisation in a polar solvent such as water results in the stabilisation of the TS, which is reduced in energy c.f. no solvent being specified. For the exo TS this results in a 0.0153641 a.u (9.641120369 kcal/mol) TS stabilisation, which would result in an increased rate, as the activation energy would be reduced. The interaction distance between the two species increases during TS formation when run in water to 2.27105 and 2.27342 A, which may allow for dipolar interaction with polar water solvent molecules. Using the Arrhenius equation, and assuming that solvent effects can be neglected for reactants, this would result in an increase in reaction rate of the exo mechanism by a factor of exp(change in activation energy (joules/mol)/RT). A frequency calculation was carried out on the exo TS obtained in water solvent, and from this in Gaussian 09W a FreqChq was run at 298.15 K to obtain the following corrections to electronic energy. The thermal energy correction term at 298.15 K
| HF/3-21G | ' | ' | ' | ' |
| electronic energy | electronic energy + zero-point correction | electronic energy + thermal correction | electronic energy + enthalpic correction | electronic energy+ Gibbs free energy correction |
| at 298.15 K | at 298.15 K | at 298.15 K | at 298.15 K | |
| -605.61895534 | -605.4239933 | -605.4144543 | -605.4135103 | -605.4596513 |
Tried to calculate frequency at HF 3-21G level of theory for the exo TS calculated prior to Further Discussion with no solvent consideration. Always failed, "severe error message" always dislayed. Copied structure and pasted into new MolGroup, reoptimised at HF prior to frequency calc, etc. but could not run frequency successfully. Could not proceed with intended comparison between the TS energies at 298.15 K for Arrhenius exponential factor change. For the endo TS equivalent analysis, see below.
Endo TS(QST3) in water at HF level of theory:
QST3 in water endo TS HF level of theory
Total Energy = -605.62813170 a.u. RMS Gradient Norm = 0.00001019 a.u. Dipole Moment = 8.4664 Debye
The endo Diels-Alder reaction TS is stabilised by 0.0177635 a.u (11.14676692 kcal/mol) when carried out in water, a model polar solvent. The interaction distance between the two species increases when run in water to 2.24207 and 2.24176 A. This reflects an increase in interaction distance between the two species during TS formation, which may allow for solvent stabilisation of the TS by dipolar interactions between the polar water molecules and dipoles present in the TS. The rate of the Diels-Alder endo reaction mechanism would be expected to increase, by a factor of exp(change to activation energy (joules/mol)/RT). To calculate the factor of change, frequency calculations were carried out at HF 3-21G level of theory, and electronic correction factors at 298.15 K found using the FreqChq tool in Gaussian 09W. These results are summarised in the table below.
| HF/3-21G | ' | ' | ' | ' |
| electronic energy | electronic energy + zero-point correction | electronic energy + thermal correction | electronic energy + enthalpic correction | electronic energy+ Gibbs free energy correction |
| at 298.15 K | at 298.15 K | at 298.15 K | at 298.15 K | |
| -605.6281317 | -605.4330947 | -605.4236301 | -605.4226717 | -605.4684317 |
Comparing the electronic energy + thermal correction with that for the endo reaction in no solvent, this gives a change in TS energy (final TS in solvent-initial TS no solventat 298.15 K of -0.01815188 a.u (-47657.76457 J/mol). Entering this into exp(change in activation energy)/RT) gives an exp(-19.22) (equal to 4.47425E-09) factor change in the rate of endo reaction .
Further Discussion II. A TS(QST2) optimisation at AM1 level of theory was undertaken with endo-6 TS. The resulting TS was then entered into further optimisation calculations at HF 3-21G and DFT B3LYP 6-31G* levels of theory.
TS(QST2): The lactol was modelled at AM1 level of theory, and optimised to a minimum. Results are as below.
E(RAM1) = -0.07342337 a.u. RMS Gradient Norm = 0.00001335 a.u. Imaginary Freq = Dipole Moment = 4.4098 Debye Point Group = C1
The allylic ester was modelled, optimised to a minimum at AM1 level of theory and results are as below.
allylic ester at AM1 level of theory
Spin = Singlet E(RAM1) = -0.11108372 a.u. RMS Gradient Norm = 0.00000915 a.u. Imaginary Freq = Dipole Moment = 2.3189 Debye Point Group = C1
The product was modelled, structure cleaned, and optimised to a minimum at AM1 level of theory, as shown:
A guess TS was modelled using the intermolecular bond interaction distances specified in literature. [10]This was optimised at AM1 level f theory, giving the structure shown below.
product endo-6 at AM1 level of theory
Total Energy = -0.22370785 a.u. RMS Gradient Norm = 0.00003134 a.u. Dipole Moment = 3.6722 Debye
guess TS at AM1 level of theory
Total Energy = -0.13809247 a.u. RMS Gradient Norm = 0.00000573 a.u. Dipole Moment = 2.7053 Debye
The TS QST3 optimisation at the AM1 level of theory gave a TS with parameters shown below:
TS (QST3) result at AM1 level of theory
Total Energy = -0.13809246 a.u. RMS Gradient Norm = 0.00000697 a.u. Dipole Moment = 2.7050 Debye
This was optimised to the HF level of theory, with parameters as documented.
TS (QST3) result at HF level of theory
E(RHF) = -642.40509477 a.u. RMS Gradient Norm = 0.00000284 a.u. Dipole Moment = 4.3716 Debye Point Group = C1
This structure was entered into a DFT B3LYP 6-31G* level of theory optimisation.Results:
TS (QST3) result at dft level of theory intermolecular CC distance = 2.27346 and 2.12396 A. Total Energy = -649.79997652 a.u. RMS Gradient Norm = 0.00000599 a.u. Imaginary Freq = Dipole Moment = 3.5453 Debye
The intermolecular interaction distances favour well with the literature distances of 2.30 and 2.11 A. This indicates that the QST3 optimisation provided a good approximation of the TS w.r.t literature results.
- ↑ B. W. Gung, Z. Zhu, R. A. Fouch, J. Am. Chem. Soc., 1995,117, 1783-1788DOI:10.1021/ja00111a016
- ↑ D. R. Lide, D. Christenson, J. Chem. Phys., 1961, 35, 1374DOI:10.1063/1.1732055115.823
- ↑ 3.0 3.1 M. Bearpark , F. Bernardi , M. Olivucci , M. A. Robb, J. Am. Chem. Soc., 1990, 112, 5, 1732–1737DOI:10.1021/ja00161a012
- ↑ J. E. Rice, B. Liu, T. J. Lee, C. M. Rohlfing, Chem. Phys. Lett., 1999, 16, 1, 3, 277-284.DOI:10.1016/S0009-2614(89)87074-5
- ↑ 5.0 5.1 5.2 5.3 , M. A. Fox, J. K. Whitesell, Organische Chemie: Grundlagen, Mechanismen, Bioorganische Anwendungen, 1995, SpringerDOI:978-3-86025-249-9 Cite error: Invalid
<ref>tag; name "ja9825336" defined multiple times with different content - ↑ 6.0 6.1 , M. A. Fox, J. K. Whitesell, Organische Chemie: Grundlagen, Mechanismen, Bioorganische Anwendungen, 1995, SpringerDOI:978-3-86025-249-9
- ↑ , A. Bondi, "Van der Waals Volumes and Radii,J. Phys. Chem., 1964,68,3,441–51DOI:10.1021/j100785a001
- ↑ 8.0 8.1 E. L. Eliel, S. H. Wilen, Basic Organic Stereochemistry, 2001, New York, John Wiley & Sons, Inc.DOI:[1]
- ↑ H. Hong, M. N Kobrak, X. Shangsen, S. Hammes-Schieffer, J. Phys. Chem. A, 2000, 104, 8058-8066 DOI:10.1021/jp000449e
- ↑ K. Afarinkia, M. J. Bearpark, A. Ndibwami J. Org. Chem., 2003, 68, 7158-7166 DOI:[2]
